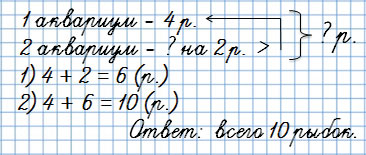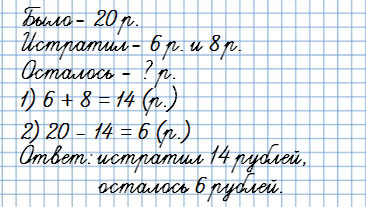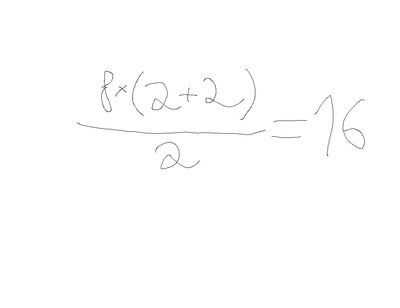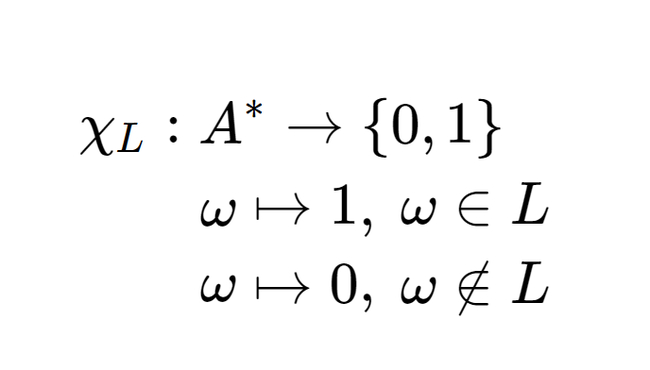Что означает на в математике в задачах
Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
Сколько грибов нашёл Володя?
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было. Стало. «
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было. Осталось. «
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали. Осталось. «
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Сколько рыбок в двух аквариумах?
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
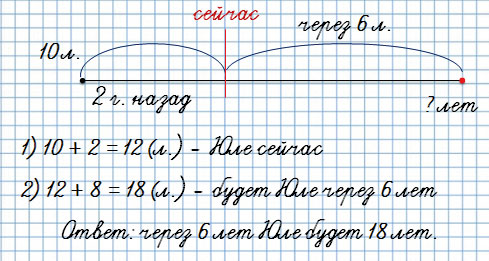
Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Поделись с друзьями в социальных сетях:
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Ученые назвали правильный ответ в спорном примере из школьного курса математики
28 июля один из пользователей опубликовал в Twitter пример из школьной программы по математике: «8:2(2+2)=?«. Обсуждение примера вызвало широкий резонанс, и перешло на международный уровень, пользователи разных стран получали ответ «16» или «1».
«На территории Российской Федерации деление и умножение имеют равные приоритеты. В США или Англии может быть другой порядок. «
А мы покупаем или продаём?
А как могло получиться не 16?
немного своровал, но все же. Сам считаю, что 1
«В Методиках преподавания алгебры Репьева В. В. (стр. 80-81) и Шустефа М. Ф. (стр. 43), по которым учили наших преподавателей алгебры в педагогических ВУЗах, однозначно сказано, что опущенный знак произведения связывает компоненты сильнее, чем знак деления. Иначе говоря, произведение без знака рассматривается как цельная величина. Вот Вам ссылки:
Также считают и калькуляторы в инструкции которых есть знак «Умножение, где знак умножения опущен». Этот знак по приоритету стоит выше деления.
Прилагаю инструкцию, смотрите страницу R-8.
28 июля, ага, смешно. Почему тогда я уже два года эти чертовы баяны собираю?
Если у нас по центральным новостям выходят такие статьи, да ещё и такого размера, то это несколько ж наипнулось наша система образования?
Я даже не сразу понял, как тут вообще получить 1.
Восемь золотых монет надо разделить между двумя родами (8:2) в каждом из которых по две семьи без детей (2+2): 8:2*(2+2). Ну дайте им по 16 монет, чо?
(для минусаторов: стебусь)
Арифметика начальной школы. Это за гранью добра и зла. Как вообще можно об этой хуйне спорить взрослым людям? Мир ебанулся и свесил мозги в каменный век.
что странно, но я откуда то помню, что сначала выполняются операции умножения, а потом деления,
С поправкой на синтаксис языков программирования это выражение будет выглядеть вот так 8/2*(2+2).
В языках Javascript, Python, Haskell, Java и PHP значение этого выражения равно 16. Так что у программистов вот так.
А я ещё вчера писал, что ответ 16.
Затянувшаяся реформа образования
Про гуманитария, математику и репетитора
Довелось учиться в позднем СССР/перестройку. В школе отставала по математике.
С ней была просто беда. Так, как по остальным предметам училась хорошо, математику мне «натягивали». Но в выпускном классе математику стала вести молодая амбициозная преподавательница, которая ставила то, что заслужил.
Итог: мне грозила двойка по математике и справка вместо аттестата.
Моя мать подсуетилась и наняла мне преподавательницу из технического ВУЗа. Очень приятную женщину в возрасте, еврейку. Таких мягких и очаровательных людей я редко встречала в жизни. С первого же урока я начала что-то понимать. Каждый урок шел буквально за год. Встречи были как праздник.
Контрольную годовую я написала на 5, и, одна единственная в классе, верно решила дополнительное задание. Учителя не понимали: я у кого-то списала? Но у кого, ведь никто не решил дополнительное задание!
Много лет мучительных страданий и всего несколько уроков у талантливого педагога.
Ну логично же ответил
Олимпиада по математике 3 класс
Что такое вектор в математике?
Сегодня на занятии мы определим, что такое вектор, каких видов он бывает и разберёмся, как совершать действия с векторами.
Подобные треугольники
Сегодня мы вспомним, что такое подобне треугольники и по каким признакам понять, что они подобны.
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
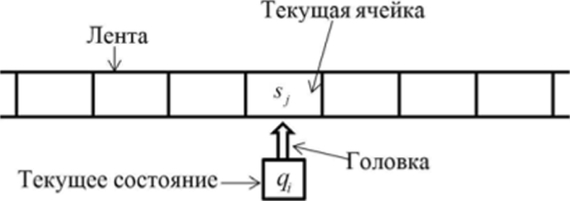
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
— выводит 1, только если w входит в язык L;
— для любого w в языке L существует такое c, что V(w,c) = 1.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
— функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
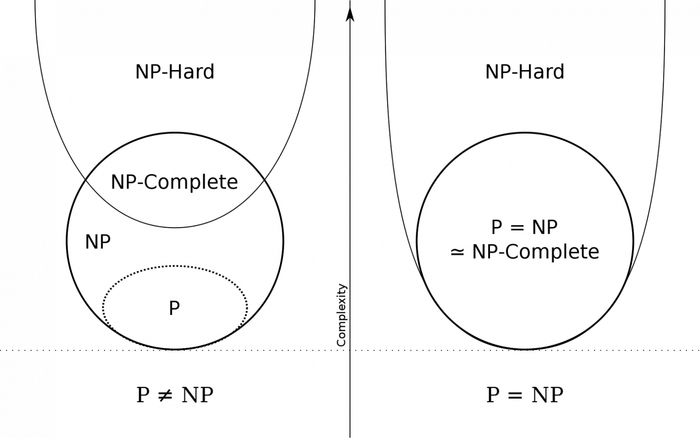
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.