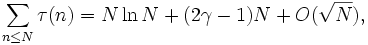Что означает неполное частное

Неполное частное

Делимость — одно из основных понятий арифметики и теории чисел, связаное с операцией деления.

Содержание

Определение

Обозначения

Связанные определения

Свойства

Число делителей

Обобщения

Понятие делимости обобщается на произвольные кольца, например кольцо многочленов.

См. также

Полезное

Смотреть что такое «Неполное частное» в других словарях:

Дробь — Если делится какое нибудь целое число а на другое целое число b, т. е. ищется число x, удовлетворяющее условию bx=а, то могут представиться два случая: или в ряду целых чисел найдется число х, которое этому условию удовлетворит, или же окажется,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Деление с остатком — Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.… … Википедия

Остаток от деления — в арифметике один из результатов операции деления с остатком. Образуется, если результат деления не может быть выражен целым числом, при этом остаток от деления должен быть по абсолютной величине меньше делителя. В случае, если числа… … Википедия

Фундаментальные алгоритмы — Два основных фундаментальных алгоритма это алгоритм деления и алгоритм Евклида Алгоритм деления предназначен для вычисления неполного частного и остатка от деления двух целых чисел. Алгоритм деления a делимое b делитель q неполное частное r –… … Википедия

Целая часть — График функции «пол» (целая часть числа) … Википедия

Преобразование Гаусса — В математике, преобразование Гаусса (измеримая) динамическая система на отрезке [0,1], заданная отображением где обозначает дробную часть числа. Это преобразование «стирает» первое неполное частное в разложении числа в цепную дробь: Кроме… … Википедия

Единая сетевая разметка — (ЕСР) система цифрового обозначения железнодорожных станций на территории стран СНГ и Балтии. С помощью кодов ЕСР кодируются станции, открытые для выполнения грузовых операций, производящие перевалку грузов с железнодорожного на речной или… … Википедия

ЗНАНИЕ В АРАБО-МУСУЛЬМАНСКОЙ ФИЛОСОФИИ — ЗНАНИЕ В АРАБО МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. Благодаря слитости процессуального и субстанциального аспектов в категории масдара (отглагольного существительного) арабское языковое мышление имеет тенденцию рассматривать процесс и результат как нечто … Философская энциклопедия

ЗНАНИЕ В АРАБО-МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. — ЗНАНИЕ В АРАБО МУСУЛЬМАНСКОЙ ФИЛОСОФИИ. Благодаря слитости процессуального и субстанциального аспектов в категории масдара (отглагольного существительного) арабское языковое мышление имеет тенденцию рассматривать процесс и результат как нечто… … Философская энциклопедия

Источник

Что такое частное в математике?

Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.

Деление

В математике есть четыре простейших операции:

Если мы говорим о частном, то нас будет интересовать такая операция, как деление.

Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое. Есть ряд символов, которые обозначают его:

В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.

Частное рассказывает, во сколько раз одно число больше другого.

Наглядные примеры

Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.

Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:

Запишем простой пример из математики:

80:2=40

80 – делимое (оно делится)

2 – это делитель (на него разделяют)

Восемьдесят больше, чем сорок, в два раза.

Другой пример выглядит так:

120:2=60

Сто двадцать больше, чем шестьдесят, в два раза.

Проверка

Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:

Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.

Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.

Полное и неполное частное

В результате проведения математических подсчетов частное может быть двух видов:

100:2=50

50 – полное частное

51:2=25 (остаток 1)

25 – неполное частное

1 – остаток от деления

Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:

30:6=x

Чтобы найти частное, следует делимое разделить на делитель:

Ответ 5 – это частное в данном примере.

Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.

Источник

Значение частного двух чисел в математике

Что такое частное чисел

Частное чисел – это результат деления одного числа на другое. Оно показывает, сколько раз число a содержится в числе b.

Деление как операция

Деление – арифметическая операция, обратная умножению, суть которой заключается в нахождении одного из сомножителей по произведению и другому множителю. В данном случае произведение переходит в делимое, имеющийся сомножитель – в делитель, искомый сомножитель – в частное.

Подобно тому, как неоднократно прибавить число – это значит умножить, так и неоднократно вычесть – это значит разделить.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На письме данную операцию можно обозначать разными символами:

Процесс деления имеет следующий вид:

В цифрах данное выражение можно записать так:

Основные свойства деления

Деление не коммутативно, то есть не перестановочно – от перемены мест элементов операции частное изменяется:

Деление не ассоциативно – то есть при последовательном выполнении деления трех или более чисел последовательность операций имеет значение, при смене порядка выполнения изменится результат:

Деление дистрибутивно справа – на одном и том же множестве две бинарные операции имеют свойство согласованности:

Имеется единственный нейтральный элемент – число 1, при делении на единицу результатом является исходное число (делимое):

Имеется единственный обратный элемент – число 1, при делении единицы на число результатом является число, обратное исходному (делителю):

Существует единственный нулевой элемент – число 0, при делении нуля на любое число результатом будет нуль:

Деление на нулевой элемент не определено:

Деление на противоположный элемент дает минус единицу:

Неполное частное

Неполное частное – результат, который получился после деления с остатком.

Под делением с остатком понимается нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Это искомое и называют неполным частным.

Разность между делимым и произведением делителя на неполное частное называется остатком, который всегда меньше делителя.

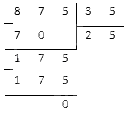
Например, 17 не делится без остатка на 5.

Наибольшее число, результат умножения которого на 5 не превосходит 17, это 3. 3 в данном случае является неполным частным.

Чтобы получить остаток, нужно из 17 вычесть произведение 3 и 5, то есть 17 – 3*5 = 2. Остаток – 2.

Изменение частного в зависимости от изменения делимого и делителя

Частное не изменится, если делимое и делить одновременно увеличить или уменьшить в одинаковое количество раз:

Задачи, примеры вычисления частного

Для того, чтобы проиллюстрировать данную арифметическую операцию, решим простые задачи.

Задача 1

В книге 891 страница. Она поделена на 9 равных глав. Узнайте, сколько страниц в одной главе.

Для этого количество страниц разделим на количество глав:

891 : 9 = 99 (страниц)

Задача 2

У Антона есть 22 апельсина. Он хочет приготовить из них компот. Для одного литра компота ему понадобится 3 апельсина. Нужно вычислить, сколько литров напитка сможет приготовить Антон и сколько апельсинов у него останется.

Источник

Общее представление о делении натуральных чисел с остатком

В данном материале мы разберем, как разделить одно натуральное число на другое с остатком. Для начала сформируем общее представление о таком действии, определимся с терминами и обозначениями, а потом посмотрим, какие задачи можно решить с его помощью. В последнем пункте попробуем объяснить, какие связи существуют между понятиями делимого, делителя, неполного частного и остатка от деления.

Общее представление о делении с остатком

Разделить с остатком – значит представить исходное множество в виде некоторого числа равных множеств и еще одного дополнительного, элементов которого недостаточно для создания требуемого множества.

В чем состоит смысл деления с остатком?

1) если b –количество элементов в каждом равном множестве, полученном после деления, то c – это количество множеств, которое у нас получилось.

2) если b – это количество множеств, то c – это число предметов в каждом из них.

Основные понятия, используемые при делении с остатком

Здесь мы определимся с основными терминами, которые будем использовать, если речь идет о делении с остатком.

Знак деления, используемый при решении примеров с остатком, аналогичен тому же знаку «разделить» (две точки, расположенные вертикально), что и при делении нацело. В некоторых источниках можно встретить обозначение « ÷ », смысл которого тот же самый. Так, числовое выражение 16 : 3 означает деление одного натурального числа на другое с остатком.

Также можно записать это в виде схемы: делимое: делитель = неполное частное (ост. остаток).

Из самого понятия о делении с остатком следует, что в любом случае остаток будет меньше делителя. Если бы он был равен ему или был нулевым, то это уже было бы деление нацело, поскольку у нас в итоге вышло бы несколько равных множеств.

Задачи, в которых используется деление с остатком

В результате процесса деления, описываемого в этой статье, всегда получаются два числа, одно из которых является остатком, а другое – неполным частным. Поэтому оно будет полезно для решения двух разных типов задач:

1. Нахождение количества необходимых равных множеств, которые можно составить из заданного количества предметов, или же количества предметов в равных множествах, полученных в результате деления.

У нас есть 67 шаров, которыми мы будем наряжать елки. Если на каждую елку нужно 15 шаров, сколько всего елок можно нарядить? Результат мы получим после деления с остатком.

Вычислять мы можем не только количество предметов, но и изменения величин (массы, времени, длины и др.)

Например, на заводе произведено 6 113 л молока. Его нужно разлить в бутылки по 2 л. Мы можем вычислить неполное частное и понять, сколько бутылок будет в итоге. Или же если на производство какого-то изделия тратится 3 часа, то мы можем найти, сколько можно их выпустить за один восьмичасовой рабочий день.

2. Задачи второго типа направлены на вычисление количества предметов в исходном множестве, которые остались после деления. Это могут быть не только предметы, но и величины.

Чтобы изготовить бетонную плиту, надо израсходовать 750 кг цемента. Если мы закупили 12 900 кг, на сколько плит нам хватит? Результат мы вычислим в результате деления с остатком.

Основные связи между понятиями делимого, делителя, неполного частного и остатка от деления

Для установления этих связей сразу разберем конкретный пример.

Если у нас есть значения делителя, неполного частного и остатка, мы можем найти делимое. Если мы объединим все имеющиеся кучки и добавим к ним остаток, то получим множество из исходного количества предметов.

Чтобы найти делимое, нужно сложить остаток с произведением делителя на неполное частное.

Верное равенство, полученное в итоге, будет полезно для решения задач с неизвестным делимым, то есть таких, где нужно найти исходное число предметов. Приведем пример:

Вычислите делимое, если неполное частное равно одиннадцати, остаток двум, а делитель семи.

Решение

Если нам известны значения делимого, делителя и неполного частного, то мы можем найти остаток.

Чтобы найти остаток от деления одного натурального числа на другое, нужно вычесть из делимого произведение делителя на неполное частное.

Решение

Если нужно найти неполное частное, нужно из делимого вычесть остаток и результат разделить на делитель.

Решение

Отнимем остаток от делимого и результат разделим на делитель. Считаем: ( 221 − 13 ) : 52 = 208 : 52 = 4 (для подсчета мы использовали метод подбора частного).

Найти делитель можно, если вычесть из делимого остаток и получившуюся разность разделить на неполное частное.

Возьмем пример решения такой задачи.

Решение

Источник

Конспект «Неполное частное и остаток»

Схема технологической карты урока математики

Планируемые образовательные результаты

— вспомнят, что такое неполное частное и остаток;

— закрепят знания на практике;

— смогут самостоятельно выполнить задание.

— проявлять положительное отношения к школе, учебной деятельности на уроке математики;

— создавать условия для развития речи, мышления, внимания, памяти учащихся;

— воспитывать любовь к математике;

— развивать практические умения, интеллектуальные и коммуникативные общеучебные умения.

осуществлять поиск необходимой информации в учебнике для выполнения учебных заданий;

проводить сравнение, обобщать, устанавливать причинно-следственные связи;

строить логическое рассуждение, включающее установление причинно-следственных связей

определять цель своей деятельности;

планировать свои действия в соответствии с поставленной задачей;

контролировать свою деятельность по ходу или по результатам выполнения задания;

оценивать правильность выполнения действия.

умение слушать и вступать в диалог;

инициативно сотрудничать в поиске и сборе информации;

излагать свое мнение и аргументировать свою точку зрения;

высказывать суждения с использованием математических терминов и понятий;

взаимодействовать (сотрудничать) с соседом по парте.

Урок закрепления полученных знаний

Методы и формы обучения

Методы: частично-поисковый, словесный, практический.

Формы: индивидуальная, фронтальная.

УМК «Перспективная начальная школа»

ТСО, тетрадь, учебник, карандаш, ручка.

Основные понятия и термины

Неполное частное, остаток, делимое, делитель.

Работа у доски, в рабочей тетради.

Диагностика результатов урока

Где мы можем применять свои знания?

Этап мотивации (самоопределения) к учебной деятельности

(Проверка готовности рабочих мест)

-Прозвенел звонок веселый

Мы начать урок готовы,

Будем слушать, рассуждать,

И друг другу помогать.

— Проверьте глазами принадлежности: дневник, пенал, учебник, рабочая тетрадь.

-Чтобы работа на уроке прошла удачно, выполним разминку.

Подготавливают рабочие места к уроку.

Настраиваются на работу.

Установка на доброжелательное отношение к участникам совместной деятельности. Осознание важности каждого урока в школе.

Этап актуализация и фиксирование индивидуального затруднения в пробном действии

а) 60 ∙ 6 б) 20 ∙ 2 в) 490:70 г) 40 ∙ 10

-Назовем тему урока, вставьте пропущенное слово на слайде.

Тема урока: «Неполное частное и (остаток) ».

-Какова же тема нашего урока?

-Какую цель предстоит решить на уроке?

-Вы были близки, я уточню ваши предположения.

Цель урока: «Закрепление знания о понятиях «неполное частное» и «остаток».

-Какие задачи предстоит решить на уроке?

Ответить на этот вопрос вам помогут незаконченные предложения на слайде:

— вспомним, что такое неполное частное и остаток;

-закрепим знании на практике;

-проявим свои знания при выполнении самостоятельного задания.

-Приступим к решению первой задачи.

-Повторим, как называются числа при делении с остатком.

(учитель показывает на числа, а ученики хором называют. Сначала называют в строке компоненты деления, а потом при решении столбиком)

-Что такое неполное частное?

-Вспомним правило, как получить делитель, используя неполное частное и остаток. Вставьте слова в правило.

(на экране слайд правила с пропущенными словами).

-Чтобы работа была не только успешной, но и дружной, выполним работу в парах. Для этого вспомним правила работы в парах.

-Послушайте задание. У одного из вас будет лежать белая карточка на столе. Задание на ней вы выполняете вместе. Вам необходимо получить делимое, используя правило. На выполнение задания отводится 2 минуты, свою готовность покажите, сложив руки домиком.

1) 28:5= 2)47:9= 3) 29:4= 4)58:8=

-Какие ответы у вас получились?

Учащиеся слушают задание и отвечают на вопрос, демонстрируя.

Тема урока: «Неполное частное и (остаток) ».

Цель урока: «Закрепление знания о понятиях «неполное частное» и «остаток».

— вспомним, что такое неполное частное и остаток;

-закрепим знании на практике;

-проявим свои знания при выполнении самостоятельного задания.

Делимое, делитель, неполное частное, остаток.

Неполное частное-это целая часть числа.

Если (делитель) умножить на (неполное частное) и к полученному результату прибавить (остаток), то в итоге получится (делимое).

Правила работы в парах:

Выслушай мнение каждого.

Умение отвечать на поставленный вопрос.

освоение способов вычисления и установления взаимосвязи между предметами.

Этап построения проекта выхода из затруднения

-Приступим к решению второй задачи.

-Выполним деление с остатком. Один ученик у доски, остальные в тетради.

-Найдем, вторую цифру делителя, используя неполное частное.

-Чтобы продолжить выполнять работу дальше, необходимо набраться сил.

Умение отвечать на поставленный вопрос.

осмысление математических действий и величин.

А теперь, ребята, встали

Быстро руки вверх подняли,

В стороны, вперед, назад

Повернулись вправо, влево,

Тихо сели вновь за дело.

Умение отвечать на поставленный вопрос.

Этап закрепления с проговариванием во внешней речи

-Решим задачу на покупки.

-(Имя) прочитай задание.

-Что известно в задаче? Лена имеет 300р.

-Нам известно сколько стоит 3 тарелки? Не известно.

-Какова цена 1 тарелки? 43 руб.

-Какова цена одного чайника? Один чайник стоит 100р.

-Нам известно сколько сдачи получила Лена? Нет известно.

-Как звучит требование задачи? Необходимо узнать сколько стаканов сможет купить Лена на сдачу.

-Как узнать цену трех тарелок? Надо 43 умножить 3.

1)43  3=129(р.)-стоит 3 тарелки.

-Как узнать стоимость покупки, зная цену тарелок и чайника? Надо к 129 прибавить 100.

2) 129+100= 229 (р.)-стоимость покупки.

-Как выяснить сколько сдачи получит покупатель? Надо из 300р. вычесть 229.

-Как узнать какое количество стаканов можно приобрести на эту сумму? Надо 71:50.

4) 71:50=1 (ост.21) – один стакан сможет купить покупатель.

-мы ответили на требование задачи?

-Какой ответ получили?

У Лены есть 300 рублей, и ей нужно купить три тарелки и один чайник. Лена решила на все оставшиеся деньги купить стаканы. Сколько стаканов она сможет купить?

осмысление математических действий и величин.

освоение способов вычисления и установления взаимосвязи между предметами.

Этап самостоятельной работы с самопроверкой по эталону. Итог урока

-Приступим к решению третьей задачи. На выполнение задания вам отводится 10 минут. Вам необходимо выполнить деление с остатком. Все вычисления делайте на карточке. Напишите свое имя и фамилию.

освоение способов вычисления и установления взаимосвязи между предметами.

Этап рефлексии учебной деятельности на уроке

-Давайте вернёмся к началу урока.

Какую цель мы ставили пред собой?

– Для этого продолжите фразы:

— Домашнее задание: стр.55, №162 (у.)

— Благодарю всех вас за работу.

Самооценка на основе критерия успешности

Формулирование и аргументирование своего мнения.

Элементарные навыки самооценки результатов своей учебной деятельности.

Умение отвечать на поставленный вопрос.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1585768

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

При засыпании человеческий мозг может решать сложные задачи

Время чтения: 1 минута

Зарплаты педагогов Ростовской области вырастут в среднем на 10-15%

Время чтения: 2 минуты

Большинство родителей в России удовлетворены качеством образования в детсадах

Время чтения: 2 минуты

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник