Что означает один ноль один
Почему 0 = 1
Споры о науке
143 поста 1.2K подписчика
Правила сообщества
Уважайте оппонентов и аргументируйте свои доводы. Ссылки на соответствующую литературу приветствуются.
1) Подписаться на меня.
2) Поставить лайк
>»говорилось на школьных курсах математики: не существует одного факториала у двух чисел»
А дальше вообще полная бредятина написана, даже комментировать не хочу.
Сейчас всё это и проверим на твоем рейтинге. Уже 88. Скоро будет 0, а там и минуса пойдут
>> Вы задолжали еще одну лошадь. Сколько у вас лошадей? У вас минус одна лошадь или ноль
едЕница у него, что вам ещё нужно?
Есть значительно более изящные доказательства того, что все рациональные числа равны. Там ошибки искать куда интереснее.
Значит кредит вы возвращать не собираетесь?
Аналогия не является научным методом.
Да кому ты нужен, не ноль и не единица?
Затянувшаяся реформа образования
Решил, что буду бесплатно проверять у учеников ежедневные задания
Я преподаватель по математике и с 1 октября 2021 я открываю подготовку к профильной математике ЕГЭ 2022 для всех желающих бесплатно. Подготовка будет идти до самого экзамена. Подробнее можете прочитать о том, как все будет происходить, в моем предыдущем посте на Пикабу.
Решил, что занятия будут полезнее, если к ежедневным заданиям добавить еще и проверку мной работ учеников.
Я буду выборочно проверять работы учеников и писать комментарии ученикам лично, отдавая приоритет тем работам, которые присланы раньше других. А самые полезные для всех моменты из работ буду комментировать для всех. Но предостерегаю, что все это бесполезно без вашей собственной работы и выработки правильных привычек, которые кратно ускоряют обучение. Поэтому и пишу этот пост-дополнение.
Подготовка будет проходить здесь. Изучайте.
О правильных образовательных привычках для учеников я пишу здесь.
Бесплатно помогаю готовиться к профильному ЕГЭ по математике
Недавно я написал о том, как финансовые проблемы у некоторых моих учеников летом помогли мне придумать, как помочь тем, кто хочет сдать ЕГЭ профиль по математике, но не может или не хочет за это платить деньги.
Подготовка будет происходить здесь. Каждый день я буду публиковать задания на день с пошаговыми разборами и отвечать на вопросы по ним. Обязательно подпишитесь на канал, так как пропускать задания не очень хорошо и лучше держать темп ровным, уведомления помогут в этом. Там есть описание, как все будет происходить, а также есть ссылка на пример задания, примерно из середины курса. Он только для примера. На нем можно пощелкать и понять, как смотреть подсказки.
Делать ежедневные задания, их решения и отвечать на вопросы мы будем с вместе с еще одним преподавателем-математиком Дмитрием. Одному было бы тяжело.
Подписанных уже 100 человек, значит точно начинаем. Присоединяйтесь. Начало 1 октября 2021.
Для тех, кто хочет почитать мои мысли, о том, как нужно организовывать обучение, можете посмотреть мою телегу.
Как сделать репетитора бесплатным
Я преподаватель математики. Уже давно готовлю ребят к профильному ЕГЭ по математике. У меня уже сложилась своя методика подготовки, которая из года в год показывает неплохие результаты.
Время от времени у кого-нибудь из учеников случаются финансовые сложности, то ковид, то еще что-то. Таким ученикам, я всегда предлагаю позаниматься бесплатно. Вот и в начале этого лета родители Никиты сообщили мне о трудностях и сказали, что далее обучаться он не сможет. Я предложил продолжить занятия бесплатно до конца лета, а в начале осени либо продолжить платно либо завершить обучение. За лето Никита сильно продвинулся. Осенью Никита выбрал продолжение занятий.
Из, того что я увидел за лето, я сделал интересный вывод. При достаточном уровне прилежности ученика вполне можно построить такую методику, которая будет давать ученику то же самое, что и очные занятия. К сожалению, думаю, что, если ученику особо математика не сдалась, то эффекта от такой подготовки не будет.
Как я работал с Никитой
Каждый день я высылал задание на день, рассчитанное примерно на 0.5-1.5 часа самостоятельной работы.
Разрешение возникающих вопросов
Если все же не получалось решить, то Никита писал мне в WhatsApp, и я присылал ему 1-2 шага решения. Если опять не получалось, то я присылал ему все решение. Обычно это снимало все вопросы.
Если все же остались какие-то вопросы, то он мог задать мне два вопроса в день, и я развернуто ему на них отвечал. Этого было достаточно.
Как решен вопрос с теорией
По каждой теме мной составлена последовательность задач от элементарных (которые может решить каждый) до задач уровня ЕГЭ. Эту последовательность я отлаживал последние пять лет. Удалось сделать так, что основные теоретические моменты включены в решения задач. Поэтому, прорешав последовательность и получив ответы на возникающие вопросы, ученики отлично усваивают теорию.
Приращение сложности от одной задачи к другой минимальное. Поэтому большинство учеников, решив предыдущую задачу, решат и следующую. Так, на дистанции в 10-20 задач незаметно произойдет уже заметное приращение сложности, которое без такой цепочки задач преодолеть было бы практически невозможно.
Раз в неделю Никита решал пробник и записывал свои результаты в табличку, где всем был виден прогресс.
Не так давно стал вести телеграм-канал о том, как организовать обучение, как сделать обучение эффективным, а также ответы на частые вопросы родителей и учеников: https://t.me/dobraya_problema
В результате чего происходит обучение ученика
Я учитель математики. И по роду деятельности постоянно разговариваю с учениками и их родителями на предмет того, что полезно для обучения, а что нет. И часто вынужден говорить «это хорошо, а это плохо». Мне такая ситуация очень не нравится, потому что обосновывать приходится каким-то птичьими обоснованиями типа «так всегда было», «школа такая-то или такая-то» или «британские ученые доказали».
Поэтому решил сформулировать свое представление о базисе, на основании которого можно будет потом делать хоть сколько-нибудь обоснованные выводы. Не судите сторого. Это моя попытка по-простому с помощью аналогий рассказать, как я это представляю ))
Нейроны могут либо возбуждаться в какой-то ситуации, либо не возбуждаться. Возбуждаются они только если поступил определенный сигнал из органов чувств.
Например, если увидеть треугольник, то возбудится нейрон, который отвечает за фигуру треугольник. Он узнает только ее. Причем этот треугольник может быть нарисован на листе бумаги, а может быть, это форма крыши увиденного дома. В обоих случаях нейрон треугольника будет зажжен. В случае, если треугольник был на бумаге, то зажжется еще нейрон, который всегда зажигается при виде бумаги, и еще тысячи других мелких нейронов. Если треугольник был распознан как фигура крыши дома, то зажгутся нейроны дома, крыши, может быть, у кого-то нейроны дождя и т.д.
Некоторые нейроны могут зажигаться не в результате получения сигнала органами чувств, а в случае, если зажглась какая-то комбинация нейронов.
Например, если человек увидел приближающееся к нему животное, то зажгутся нейроны животного, нейроны приближающегося объекта, нейрон размера объекта, нейрон вида объекта. Для простоты допустим, что есть нейрон, который зажигается, когда зажигается комбинация: объект приближается, хищник, большой. Предположим, этот нейрон зажегся. Назовем этот нейрон «нейрон большой зверь идет в мою сторону». Пусть есть нейрон, который зажигается всегда, когда зажигается нейрон «нейрон большой зверь идет в мою сторону». Пусть это будет нейрон «бежать» и т.д.
Решение задач по математике тоже происходит в результате последовательности зажиганий нейронов.
Например, пусть ученик увидел условие задачи, в которой дан прямоугольный треугольник и известны два катета, а найти нужно гипотенузу. В голове образованного ученика зажжется нейрон прямоугольный треугольник. Всегда, когда зажигается нейрон «прямоугольный треугольник» у обученного геометрии человека зажигается нейрон «теорема Пифагора». Если есть два катета и горит нейрон «теорема Пифагора», то зажигается нейрон «я знаю, как найти гипотенузу, зная два катета» и т.д.
Что такое образованность
Образованность в конкретной области — это наличие наработанных цепочек зажигающихся нейронов, которые регулярно приводят к правильным решениям.
Как сформировать такие связи
Связь формируется, если в ответ на ситуацию человек произвел действие и в последствии оказалось, что это действие верное. Т.е. это обычная приспосабливаемость. Причем если в ответ на ситуацию человек произвел действие, а потом оказалось, что оно неверное, то обучение тоже происходит, только такая цепочка нейронов в будущем не будет зажигаться.
В результате чего происходит обучение
Нужно пробовать решать задачи. Нужно решать задачи, которые учитывают уже имеющиеся нейронные связки.
Бесполезно решать легкие задачи: связи уже есть и вы просто их укрепляете, и это укрепление будет даже немного мешать формировать новые связи.
Бесполезно решать слишком сложные задачи, так как не хватает очень больших участков цепи нейронов. И есть риск, что она будет сформирована неправильно, если вы даже где-то прочтете решение.
Нужно решать задачи, которые требуют приращения «одного» звена к цепи нейронов.
Читать теорию, а потом решать задачи менее эффективно, чем просто решать задачи, если эти задачи выстроены в цепочку, где каждая следующая задача требует наличия всего одного звена в нейронной цепочке. Но очень часто люди сначала слушают теорию, а потом пробуют решать задачи. Это происходит потому, что состояние нейронных цепочек у всех разное и подобрать такую последовательность задач индивидуально сложно и проще сначала рассказать теорию, а потом всем решать одни и те же задачи.
Буду рад камментам с предложениями по улучшению/сокращения/исправлению этого объяснения для родителей и учеников!
В своем телеграм-канале отвечаю на частые вопросы родителей и учеников. Заходите.
Все знают, что на 0 делить нельзя. Но хоть кто-то задавался вопросом «почему?» (не моё)
«Делить на ноль нельзя!» — большинство школьников заучивает это правило наизусть, не задаваясь вопросами. Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя.
Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух.
Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число.
Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8.
Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения.
Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение.) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.
Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д.
Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности», но в арифметике таких случаев не встречается.)
Двоичная система для чайников
Я решил сделать серию постов по информатике для чайников.
Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.
Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.
Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.
Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:
А число 3 как три палочки:
Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:
Теперь пересчитаем – получилось 8.
Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Десятичная система счисления
Как мы складываем в 10-СС? Например, столбиком:
Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
12 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:
Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:
564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.
При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).
7000 = 7*1000 = 7 * 10^3
А всё число 7031 можно расписать так:
7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0
Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂
Двоичная система счисления
Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Теперь давайте поскладываем в двоичной системе.
Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?
Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! “1+1” складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.
Ну, и для закрепления материала сложим в 2-СС:
= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)
= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
= (10000) + (100) + (00) + (10)
= (10000) + (100) + (00 + 10)
А по-русски: 13 + 9 = 22
Большое спасибо! Очень хорошо объяснили. Всё понял.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри
поделитесь, пожалуйста, еще постами по информатике если есть
А теперь слушайте домашнее задание: построить синхрофазотрон.
Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Я тебя разочарую, но это десять и есть.
Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0
На самом деле все еще проще.
Нейронные сети. Формулы обратного распространения
Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.
Благодарим за создание выпуска:
Переводчика – Федора Труфанова;
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
Нейронные сети. Обратное распространение ошибки
Привет, Лига образования!
Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.
В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.
Благодарим за создание выпуска:
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
И бонус в комментариях, английский!
Нейронные сети. Градиентный спуск: как учатся нейронные сети
Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.
Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.
Благодарим за участие в выпуске:
Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;
Корректора – Дмитрия Мирошниченко;
Дикторов – Никифора Стасова, Дарью Яговкину;
Монтажера – Олега Жданова.
Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.
Нейронные сети. Просто о сложном
Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.
Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.
И наша первая озвучка — видео о том, что же такое нейросети.
За это отличную озвучку мы благодарим Александра Колдаева.
Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.
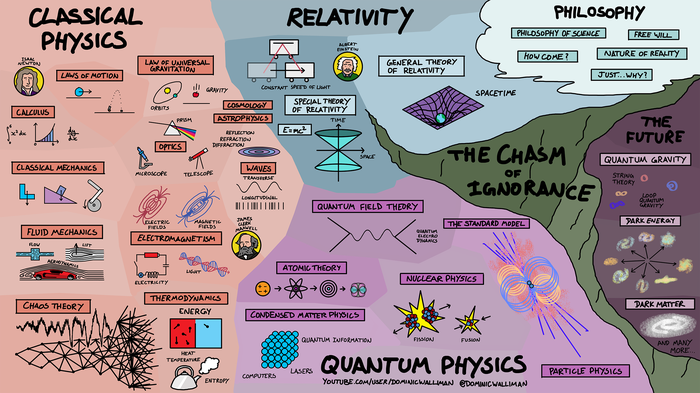
Карты наук
Выше был их автор. А вот и одна из его карт (по физике):
О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.
Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.
Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.
Вот, например, по Computer Science:
А вот по математике:
Спасибо за внимание!
За день до экзамена
Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.