Что означает округлить до десятых
Как правильно округлить число до десятых
Необходимость округления чисел
Числа округляют в случаях, когда абсолютная точность не нужна или невозможна.

С необходимостью округлять числа до требуемой разрядности для удобства, а порой и для возможности произведения расчетов, сталкиваются не только математики. Человек склонен упрощать себе жизнь, и когда особая точность расчетов не требуется, он, несомненно, округлит любую цифру.
А в случаях, когда в промежуточном расчете получается бесконечная периодическая дробь, то без округления полученного значения дальнейшие расчеты просто невозможны. И единственным выходом остается округление до приемлемой разрядности.
То самое знаменитое «пи» по умолчанию в расчетах принимается с округлением до сотых. Если же в условии задания указано «число п округлите до десятых», то его значение будет 3,1.
При решении задач из школьного учебника точность расчетов принимается по умолчанию до разряда сотых. Если только в условии задачи не указано «округлите числа до разряда десятых».
Округление чисел
Округлением числа называется математическая операция уменьшения количества знаков в числе и замены его приближенным значением заданной точности. Выполняется обнулением значащих цифр справа до заданного разряда. В зависимости от цифры, стоящей в исходном числе после цифры разряда, до которого требуется исключить число, последняя значимая цифра округленного числа может быть равна цифре исходного числа, или увеличена на единицу.
Если первая обнуляемая цифра после цифры заданного разряда меньше или равна 5, то последняя сохраняемая не меняется. Если больше пяти, последняя сохраняемая цифра увеличивается на единицу.
Округление целых чисел
Целое, или натуральное число можно округлять до десятков, сотен, тысяч и так далее. Если натуральное число требуется округлить до десятков, то цифру в разряде единиц заменяют нулем, а цифру в разряде десятков или оставляют без изменения, или увеличивают на единицу, если в исходном числе в разряде единиц была цифра 5 и больше.
Округление дробных чисел
Округление дробных чисел проводится по тем же правилам. Если требуется округлить исходное число до разряда десятых, то в итоговом числе после запятой должна быть одна цифра. Определение, какая именно, аналогично определению последней цифры при округлении натурального числа.
Разберем на примерах.
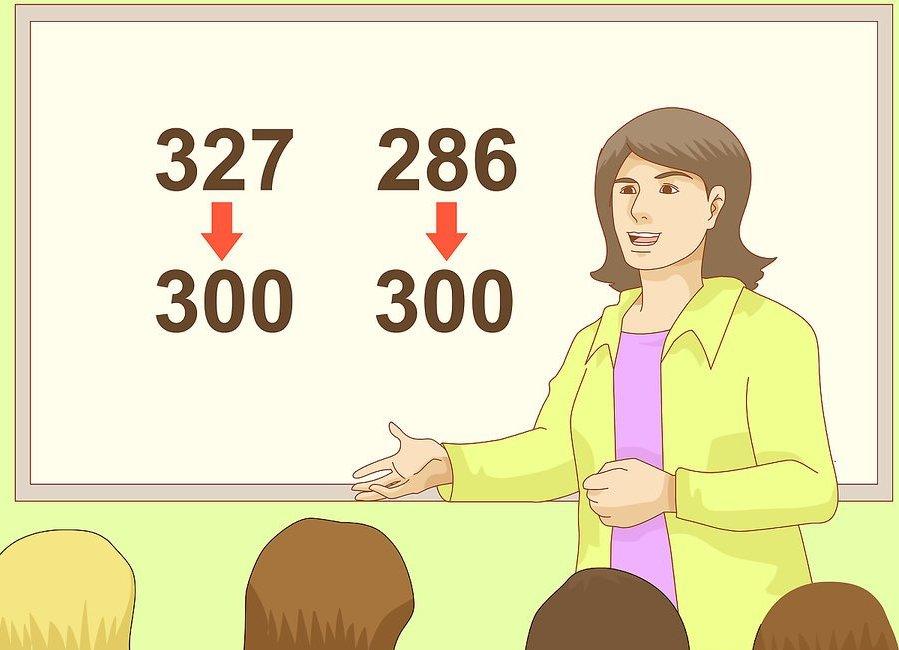
Пример 1. Как округлить число до десятых?
Пример 2. Как округлить число до десятых?
Исходное число 108,89. Правильным ответом будет 108,9, так как цифра сотого разряда больше пяти. Согласно правилам округления, требуется увеличение предыдущей цифры на единицу.
Пример 3. Как округлить число до десятых?
Исходное число 108,0489. Правильный ответ в этом случае 108,0, так как по правилам округление производится не последовательно, начиная с последней значимой цифры числа, а рассматривается цифра сотого разряда.
Но важно помнить, что, даже если в итоге у вас после запятой получается цифра «0», ее обязательно надо записать, иначе решение будет ошибочным. Без цифры после запятой у вас получится натуральное число, а в условиях задания требовалось округление до разряда десятых.
Пример 4. Как округлить число до десятых?
Исходное число 107,99. Правильный ответ 108,0.
В данном случае цифра ноль после запятой показывает, что число округлено именно до разряда десятых.
Округление десятичных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Правила округления десятичной дроби
Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.
В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:
Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).
Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.
Число, полученное при округлении, называют приближенным значением данного числа.
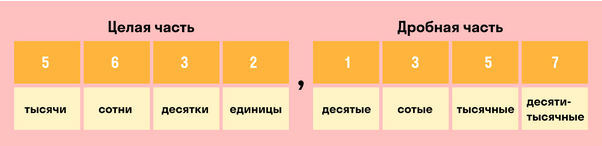
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.
Еще одно правило округления, которое нужно запомнить
Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число.
Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Примеры округления десятичной дроби
Давайте разберем несколько примеров округления дробной части десятичных дробей.
Пример 1. Округлите дробь 56,786 до сотых.
Цифра, которую нужно округлить, — 8. Обращайтесь к таблице с подсказками названия разрядов, чтобы верно определять нужную цифру.
Справа от цифры округляемого разряда цифра 6.
Смотрим на пункт 4. Прибавляем: 8 + 1 = 9.
Пример 2. Округлите дробь 0,647 до десятых.
Округляемая цифра — 6.
Смотрим пункт 3. Значит, цифра 6 остается неизменной.
Пример 3. Округлите дробь 23,98 до разряда единиц в целой части.
Цифра, которую нужно округлить, — 3.
Первая цифра после запятой — 9. Значит, нужно прибавить: 3 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
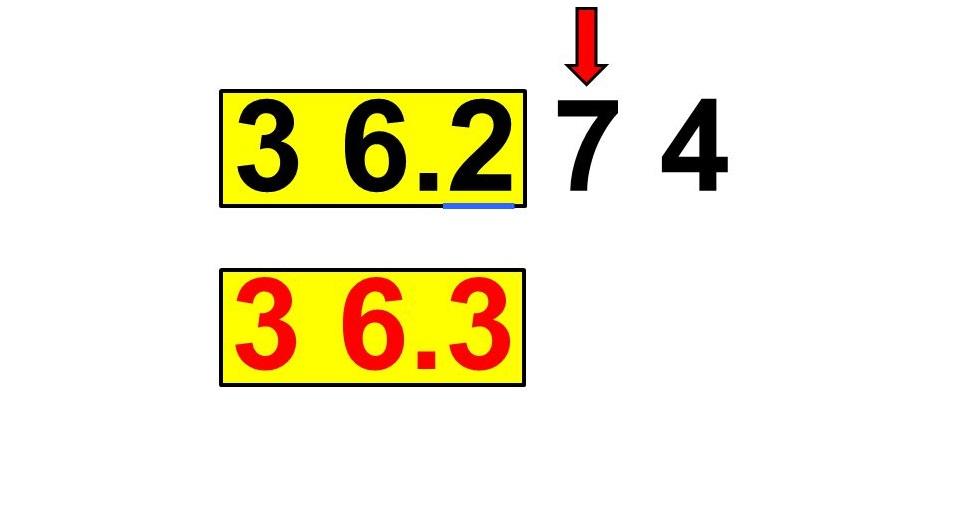
Пример 4. Округлите дробь 3,286 до десятых.
Цифра, которую нужно округлить, — 2.
Согласно правилу, прибавляем: 2 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Пример 5. Округлите дробь 45,387 до сотых.
Затем отбрасываем все остальные цифры, стоящие справа.
Как правильно округлять числа после запятой
Далеко не все умеют округлять числа правильно. Например, купив товар за 1469 рублей, чаще всего люди говорят, что потратили полторы тысячи. В целом это так, но некоторые правила округления нарушаются. Чтобы этого избежать, мы с вами поговорим о том, как правильно работать с числами.
Зачем нужно округление
Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.
Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:
Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.
Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.
Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.
Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.
Правила округления чисел
В основе округления лежат математические правила:
В метрологии — науке об округлениях и погрешностях, результат принято округлять до двух значащих цифр. Что же это значит? Значащая цифра — это цифра от первой, отличной от нуля.
Есть три случая, для которых есть свои особенности округления:
Когда мы имеем дело с числами меньше единицы, необходимо округлять результат до двух знаков после запятой. Например, число 0,7342. Округляем это число до 0,734, а потом до 0,73. Именно так и должен быть округлён результат. Первый ноль не является значащей цифрой.
Попробуем округлить 8,357. Первая цифра 8 является значащей, так как она отлична от нуля. Соответственно, нам необходимо округлить результат до одного знака после запятой. Согласно правилам, о которых мы говорили выше, результат будет равен 8,4.
Теперь самый сложный случай. Попробуем округлить 47,336. Так как все цифры отличны от нуля, мы будем округлять результат до целого числа. По математическим правилам он будет равен 47. Если мы имеем дело с трёхзначным числом, необходимо округлить результат до двух знаков, после чего умножить на 10 в нужной степени. Пример: округляем 4289,346 и получаем 43, умноженное на десять в квадрате.
Именно для того и нужна метрология, чтобы правильно округлять и записывать результат в технической документации. А также для избежания ошибок при ведении расчетов в разработке технических устройств.
Заключение
Теперь вы знаете, как правильно округлять и сможете делать все необходимые расчеты самостоятельно. Главное, доходы округлять в меньшую сторону, а расходы — в большую. И тогда вам точно будет хватать денег на все покупки, и останется небольшая сумма, которую можно потратить на развлечения. Успехов вам!
Видео
В нашем видео подробно рассказано о правилах округления чисел — с примерами.
Правила округления чисел
Вспомним правила округления.
Мы применяем их для десятичных дробей, заменяя число на его приближённое значение, записанное с меньшим количеством значащих цифр.
Зачем нам округление?
Например, вы покупаете ноутбук, диагональ которого 17 дюймов. Сколько это в сантиметрах?
Но какой практический смысл в сантиметра? Если десятая доля сантиметра – это миллиметр, то сотую долю сантиметра мы и разглядеть без лупы не сможем.
Нам удобно округлить результат до целого – до 43 сантиметров. Или, если очень хотим, до десятых. И тогда мы получим 43,2 сантиметра.
Округлить до целых – значит заменить десятичную дробь ближайшим к ней целым числом.
1) Например, десятичную дробь 4,2 мы хотим округлить до целых.
Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
Округленные числа
Онлайн калькулятор для округления чисел, до целого, разряда, десятков, сотен, тысяч. Округлить дробное число.
Если нужно округлить число, это означает, что сократится его значение до сотых, десятков или тысячных, остальные значения откидываются.
При округлении, число которое отбрасывается и будет играть главную роль. Если это чисто от 0 до 5, то округляемое число остается без изменения. Когда число от 5 до 9, округляемое число увеличивается на 1.

Нужно округлить число 35,948 до сотых.
Это означает, что цифра 8 будет откинута. При этом предыдущая цифра, а это 4 в данном случае будет увеличена на 1.
Имеем: 35,948 = 35,95
Пример:
Нужно округлить число 0,738 до десятых.
Значит, что нужно откинуть две последние цифры – 38, обращаем внимание на следующую после той, которая остается – это 3. В данном случае оно меньше 5, поэтому изменения не проводятся.
Если цифра, которая отбрасывается равна 5, то к оставшейся добавляется 1.
Когда нужно округлить, например число 0,795 до сотых, отбрасывается 5, значит к предыдущей цифре добавляется 1. Так как у нас это 9, получится 10, соответственно 7 превратится в 8: 0,795 = 0,80.