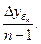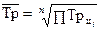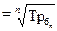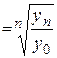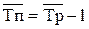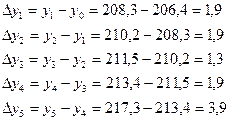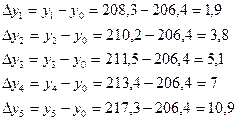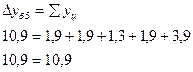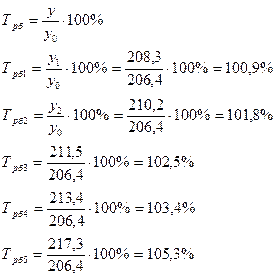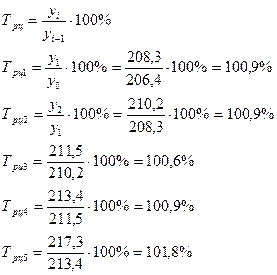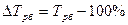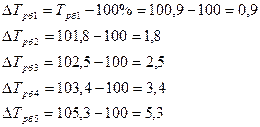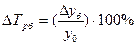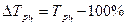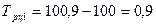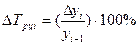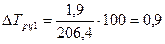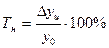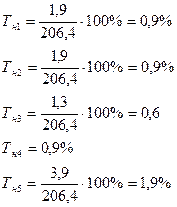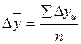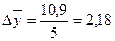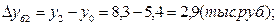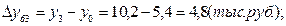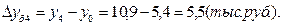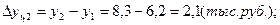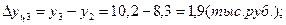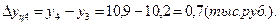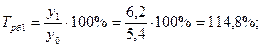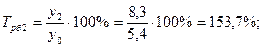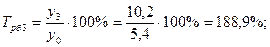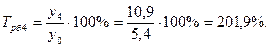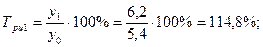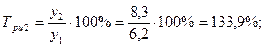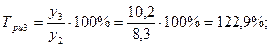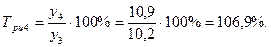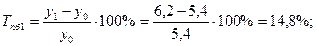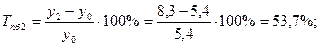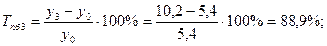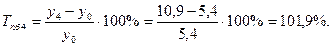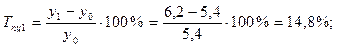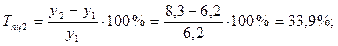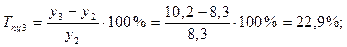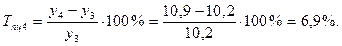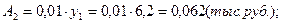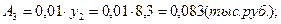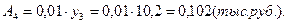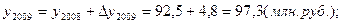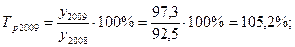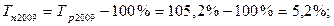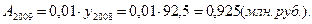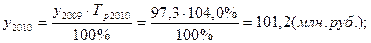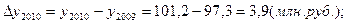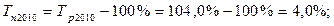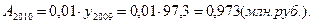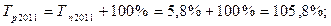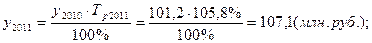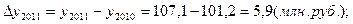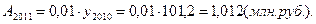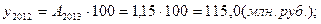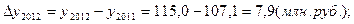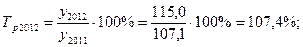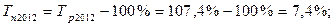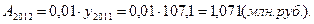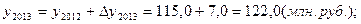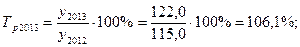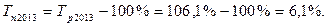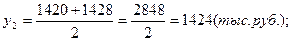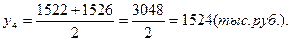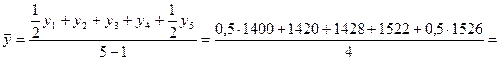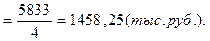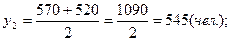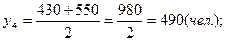Что означает относительный прирост
Показатели динамики: темп роста и темп прироста
Темп роста
Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.
Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста
Коэффициент роста может быть рассчитан по формулам:
Также темп роста может определяться так:
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.
Абсолютный прирост
Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:
1. Абсолютный прирост (цепной):
2. Абсолютный прирост (базисный):
где уi — уровень сравниваемого периода;
Уi-1 — Уровень предшествующего периода;
У0 — уровень базисного периода.
Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.
Темп прироста
Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:
Темп прироста можно получить из темпа роста:
Коэффициент прироста может быть получен таким образом:
Абсолютное значение 1%-го прироста
Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.
Примеры расчетов показателей динамики
Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики
О показателях динамики
При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.
Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.
Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.
ОТНОСИТЕЛЬНЫЙ ПРИРОСТ
Относительный прирост живой массы (D), характеризующий интенсивность роста, определяют по формуле:

где D — относительный прирост;
W o — начальная живая масса;
W I — конечная живая масса.
Смотреть что такое «ОТНОСИТЕЛЬНЫЙ ПРИРОСТ» в других словарях:
относительный прирост — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN incremental rate … Справочник технического переводчика
относительный прирост (части) поставляемой электроэнергии — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN incremented delivered powerincremented fraction of delivered power … Справочник технического переводчика
относительный прирост потерь — — [В.А.Семенов. Англо русский словарь по релейной защите] Тематики релейная защита EN incremental losses … Справочник технического переводчика
относительный прирост потерь при передаче (электроэнергии) — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN incremental transmission losses … Справочник технического переводчика
относительный прирост расхода тепла — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN incremental heat rate … Справочник технического переводчика
относительный прирост расхода топлива — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN incremental fuel rate … Справочник технического переводчика
относительный прирост стоимости (электроэнергии) — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN incremental cost … Справочник технического переводчика
относительный прирост эксплуатационных расходов — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN incremental maintenance cost … Справочник технического переводчика
ОТНОСИТЕЛЬНЫЙ РОСТ — прирост, вычисленный в % к исходной массе растения или органа … Словарь ботанических терминов
СИЛА РОСТА — относительный прирост наращенной суммы в бесконечно малом промежутке времени … Энциклопедический словарь экономики и права
Отличие темпа роста от темпа прироста
Темпы роста и прироста рассчитываются очень часто, и не только в статистике, но и в экономике, производстве и даже социологии и юриспруденции, и перед каждым студентов стоит задача, понять, что это за показатели, как они рассчитываются и чем отличаются. Зачастую студенты начинают в них путаться, давайте попробуем это предотвратить.
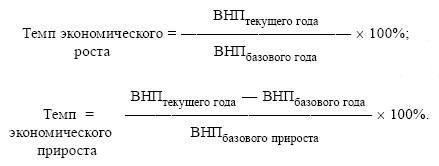
Темп роста – относительный экономический показатель, показывающий процентный рост одного показателя над аналогичным показателем прошлого периода.
Например, с помощью темпа роста вы можете посчитать, сколько ваша заработная плата в этом году составила в процентах по сравнению с прошлым годом.
Чтобы рассчитать темп роста необходимо значение текущего года разделить на значение предыдущего года и умножить на сто, так как показатель относительный и рассчитывается в процентах.
Если получилось значение больше 100 – отмечается рост, если меньше 100 – снижение.
Пример №1.1 Средняя заработная плата рабочего в 2016 году составила 33000 рублей, а в 2015 году она составляла 31 500 рублей, рассчитаем по заданным условиям темп роста. Подробнее о способах расчета темпа роста можно посмотреть в этой статье.

Темп роста = 33000/31500 * 100 = 104,76 %. Таким образом, средняя заработная плата в 2016 году составила 104,76% относительно средней заработной платы предыдущего года.
Пример №2.1 Предприятие в 2015 года имело прибыль 142 000 рублей, прибыль 2016 года составила 139 000 рублей, рассчитать темп роста.
Темп роста = 139000/142000 *100 = 97,89%. Таким образом мы видим, что показатель роста меньше 100%, а это значит, что прибыль предприятия сократилась в отчетном году. Предприятие получило 97,89% относительно 2015 года.
Определить размер роста или сокращения с ходу достаточно проблематично, чего не скажешь о другом показателе, имеющем почти тоже экономическое значение. Поговорим о темпе прироста.
Темп прироста – самый универсальный сравнительный показатель эффективности, он показывает, НА СКОЛЬКО процентов вырос или снизился один показатель по сравнению с аналогичным показателем более раннего периода. Результат определяется так – если получилось отрицательное значение – то можно говорить о темпе снижения (убыли), а если положительный о темпе роста (приросте). Этот показатель является более наглядным.
Как рассчитать темп прироста
Он рассчитывается несколькими способами, самое простое рассчитать показатель на основе темпа роста путем вычитания 100. Разберем на тех же примерах, что выше.
Пример №1.2 
Темп прироста = 33000/31500 * 100 — 100= 104,76-100 = 4,76%. Таким образом, средняя заработная плата выросла на 4,76% (+4,76%).
Пример №2.2
Как еще можно посчитать темп прироста?
Если в задании вы рассчитывали абсолютное отклонение, то можно воспользоваться данным значение и разделить его на значение базисного года, рассмотрим на примере №1.1
Абсолютное отклонение = 33000 – 31 500 = 1500 рублей.
Темп прироста =1500 / 31500 * 100%= 4,76%. Мы видим, что от смены метода расчёта итог остался неизменным, поэтому выбирайте тот способ, который вам больше нравится.
Вернемся к теме статьи, и обобщим, в чем разница между темпом роста и прироста. Разница между показателями заключается в следующем:
Если после прочтения материала вам непонятно, как рассчитать показатель или у вас остались вопросы по теме – задайте их в комментариях, не стесняйтесь.
Формула темпа прироста
Понятие и значение темпа прироста
Темп прироста используется при анализе какого-либо ряда динамики. Формула темпа прироста часто применяется в статистике и экономике в паре с таким показателем, как темп роста (в процентном соотношении).
Если в результате расчета получается положительная величина, то можно говорить об увеличивающемся темпе прироста, при отрицательном же значении происходит снижение темпа исследуемого значения, если сравнивать его с предыдущим (базисным) периодом.
Формула темпа прироста часто применяется в анализе инвестиционных проектов. Также этот показатель часто используется муниципальными организациями при расчетах:
Формула темпа прироста
Для расчета темпа прироста нужно найти отношение исследуемого показателя к предыдущему (базисному), далее из получаемого результата вычесть единицу. Окончательный результат умножается на 100, для того, что бы выразить итог в процентах. Формула темпа прироста по первому способу выглядит так:
Тп=((Пип/Пбп)-1)*100%
Здесь Тп – темп прироста,
Пбп – показатель базисного периода,
Пип – показатель исследуемого периода.
В случае, когда вместо фактического значения анализируемых показателей известно только значение абсолютного прироста, применяют альтернативную формулу. При этом находят процентное отношение абсолютного прироста к тому уровню, в сравнении с которым он и рассчитывался.
Тп=((Пип-Пбп)/Пбп)*100%
Здесь Тп – темп прироста,
Пбп – показатель базисного периода,
Пип – показатель исследуемого периода.
Отличие темпа роста и темпа прироста
Большую сложность для учащихся представляет отличие темпа роста от темпа прироста. Выделим несколько положений, в которых заключается разница между этими величинами:
Примеры решения задач
| Задание | Для предприятия ООО «Севермет» даны следующие показатели, представленные за 2015 и 2016 год: |
2015 год – 120млн. рублей,
2016 год – 110,4млн. рублей.
Известно, что в 2017 году величина дохода увеличилась в сравнении с 2016 годом на 25 млн. рублей.
На основе имеющихся данных рассчитать темп роста и прироста, сделав при этом выводы.
Здесь Тр – темп роста,
П2015 – показатель за 2015 год,
П2016 – показатель за 2016 год.
Тр=110,4млн. руб./120млн. руб. * 100% = 92 %
Темп прироста обозначает процентное соотношение изменения величины в текущем периоде в сравнении с предыдущим. Для расчета нужна формула темпа прироста:
Рассчитаем показатели за 2017 год
Тр=(120 млн. руб. + 25 млн. руб.)/120 млн. руб.= 1,21 (или 121 %)
Тп=(145 млн. руб./120 млн. руб)-1=0,208 (или 20,8%)
Вывод. Мы видим, что темп роста при сравнении 2015 и 2016 года составил 92%. Это означает, что прибыль предприятия в 2016 году уменьшилась на 92%в сравнении с 2015 годом. При расчете темпа прироста получилась отрицательная величина (-8%), что говорит о том, что прибыль компании в 2016 году (при сравнении с 2015 годом) уменьшилась на 8%. В 2017 году прибыль составила 121% в сравнении с 2016 годом. При расчете темпа прироста мы видим, что он составил 20,8%. Положительная величина говорит об увеличении прибыли именно на это количество процентов.
| Задание | Рассчитать прирост заработной платы на предприятии ООО «Севермет» за 2015 и 2016 год. Даны следующие показатели: |
Заработная плата 2015 год – 31,5 тыс. руб.,
заработная плата 2016 год – 33 тыс. руб.,
Вывод: Таким образом, мы видим, что темп прироста составил 4,8 %, что означает, что заработная плата в 2016 году по сравнению с 2015 годом увеличилась на 4,8%.
Абсолютные и относительные показатели динамики



В основе расчёта показателей ряда динамики лежит сравнительный анализ уровней ряда либо с постоянной, либо с переменной базой сравнения. При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же показателем (уровнем), принятым за базу сравнения ( 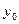
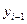
Показатели динамики с постоянной базой сравнения называются базисными, а показатели с переменной базой сравнения – цепными.
1). Абсолютный прирост – это разность между двумя уровнями ряда динамики в исходных единицах измерения:
— базисный:
— цепной:
Он показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения.
По знаку абсолютного изменения делается вывод о характере развития явления: при 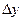
Между цепным и базисным абсолютным приростом существует взаимосвязь: сумма цепных абсолютных приростов равна абсолютному приросту последнего уровня ряда динамики:
2). Темп роста – это отношение двух сравниваемых уровней ряда, может выражаться в виде коэффициента, но чаще в %.
Цепной:
Базисный:
Он показывает, во сколько раз данный уровень ряда превышает уровень базисного периода. Если темп роста > 100%, то идёт увеличение изучаемого уровня по сравнению с базисным или предыдущим, и наоборот.
Между базисным и цепными темпами роста существует взаимосвязь – произведение последовательных цепных темпов роста равно базисному темпу роста последнего уровня ряда динамики:
Частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:
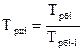
3). Темп прироста характеризует абсолютный прирост в относительных величинах. Определяется двумя способами:
а) как отношение абсолютного прироста к уровню, принятому за базу сравнения:
Базисный:
Цепной:
б) как разность между темпом роста и 100%:
Базисный:
Цепной:
Если уровни ряда динамики сокращаются, то соответствующие показатели темпов прироста будут с минусом, так как они характеризуют уменьшение ряда динамики в процентах.
4). Темп наращивания показывает рост во времени экономического потенциала. Вычисляется делением цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:
5). Абсолютное значение одного процента приростаопределяется через отношение цепного абсолютного прироста к цепному темпу прироста за соответствующий период:
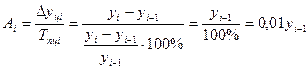
Он показывает, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов.
6). Относительное ускорение представляет собой разность следующих друг за другом темпов роста (прироста) в одном ряду или темпов роста (прироста) за один период в двух смежных рядах динамики:
Относительное ускорение выражается в процентных пунктах роста. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно складывать, в результате чего получается темп прироста соответствующего периода по сравнению с базисным уровнем.
7). Коэффициент опережения определяется как отношение последующего темпа роста (прироста) к предыдущему или через соотношение темпов роста или темпов прироста за одинаковые периоды времени по двум динамическим рядам:
С помощью коэффициентов опережения сравнивают динамические ряды одинакового содержания, но относящиеся к разным территориям (странам, регионам, районам) или к различным организациям (министерствам, предприятиям), а также ряды разного содержания, характеризующие один и тот же объект (рост потребительских цен и рост среднемесячной зарплаты за одни и те же периоды времени).
Средние показатели
1). Средний уровень ряда динамики– это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности, он характеризует типическую величину абсолютных уровней ряда и зависит от вида ряда динамики:
а) для интервального ряда абсолютных величин с равными периодами (интервалами времени) используется средняя арифметическая простая:
б) для моментного ряда с равными интервалами между датами применяется средняя хронологическая:
в) для моментного ряда с неравными интервалами между датами рассчитывается средняя арифметическая взвешенная:
где 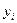
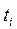
2). Средний абсолютный прирострассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени:
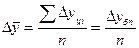
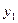
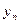
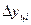
3). Средний коэффициент роста можно определить, пользуясь формулами:
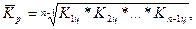
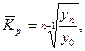
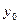
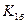
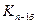
Средний коэффициент роста показывает, во сколько раз в среднем за отдельные составляющие рассматриваемого периода времени изменились уровни динамического ряда.
4). Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:
5). Средний темп прироста:
Таблица 2.1. Уровни (показатели) ряда динамики
| Показатель | Формула | ||||||||||||||||||||||||
| Абсолютный прирост | Δ 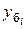 = yi – у0 = yi – у0 | ||||||||||||||||||||||||
| Темп роста | 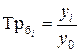 | ||||||||||||||||||||||||
| Темп прироста | 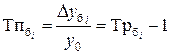 | ||||||||||||||||||||||||
| Абсолютный прирост | Δ 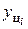 = yi – yi-1 = yi – yi-1 | ||||||||||||||||||||||||
| Темп роста | 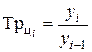 | ||||||||||||||||||||||||
| Темп прироста |
| Показатель | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 |
| Производствен-ная мощность т/сутки | 206,4 | 208,3 | 210,2 | 211,5 | 213,4 | 217,3 |
1. Все аналитические показатели ряда динамики.
2. Взаимосвязь цепных и базисных темпов роста.
3. Привести графическое изображение динамики производственной мощности.
1). Абсолютный прирост
Цепные:
Базисные:
Базисные:
Цепные:
Базисные: 1-й способ:
2-й способ:
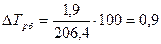
Цепные: 1-й способ:
2-й способ:
4). Темп наращивания:
5). Средний абсолютный прирост:
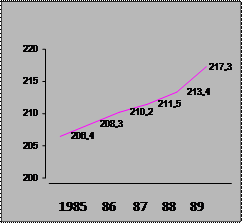 |
Рис. 1. Динамика производственной мощности
Среднемесячные денежные доходы на душу населения по области составили (тыс. руб.):
| 2006 | 2007 | 2008 | 2009 | 2010 |
| 5,4 | 6,2 | 8,3 | 10,2 | 10,9 |
Определить цепные и базисные показатели динамического ряда.
1). Абсолютные приросты:
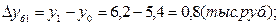
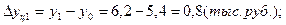
4). Абсолютное значение одного процента прироста:
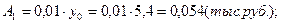
Используя взаимосвязь показателей динамики, определить уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным:
Производство продукции, млн. руб.
По сравнению с предыдущим годом
Решение оформить в таблице.
Исходная таблица приобретает вид:
Производство продукции, млн. руб.
По сравнению с предыдущим годом
Имеются данные об остатках вкладов физических лиц в отделении банка, тыс. руб.:
— на 1 октября – 1522;
— на 1 января следующего года – 1526.
1) средний остаток вкладов населения в каждом квартале;
2) средний годовой остаток вкладов населения.
1). Средние остатки вкладов населения по кварталам:
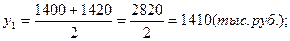
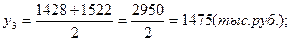
2). Среднегодовой остаток вкладов населения для моментного ряда с равными интервалами определяется по формуле средней хронологической:
Списочная численность работников организации в прошлом году составила: на 1 января – 530 чел., на 1 марта – 570 чел., на 1 июня – 520 чел., на 1 сентября – 430 чел., а на 1 января текущего года – 550 чел. Вычислить среднегодовую численность работников организации за минувший год.
По условиям задачи имеется моментный ряд динамики с неравными интервалами времени: t1=2 месяца, t2=3 месяца, t3=3 месяца, t4=4 месяца.
Среднесписочные численности работников за каждый из этих периодов:
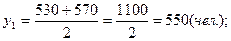
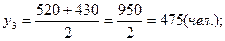
Среднегодовое значение численности работников необходимо рассчитывать по формуле средней арифметической взвешенной:
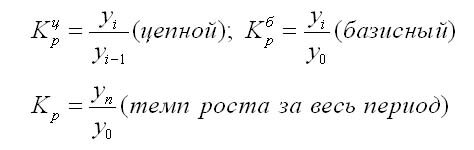
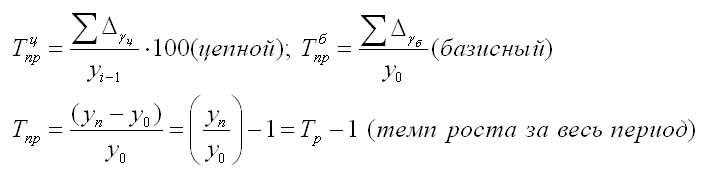
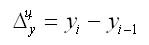
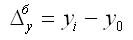
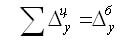
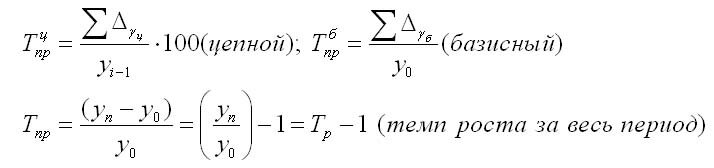
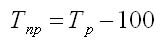
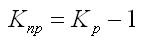
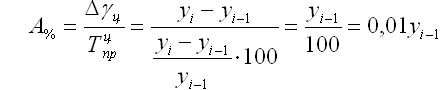



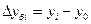
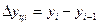
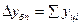
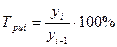
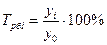
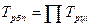
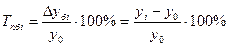
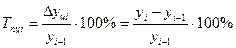
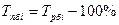
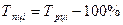
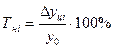
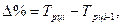
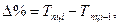
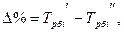
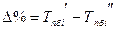
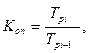
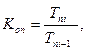
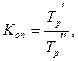
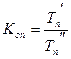

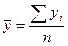
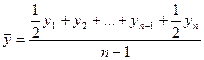
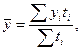
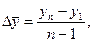
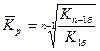
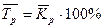
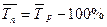
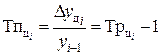
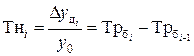
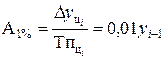
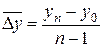 =
=