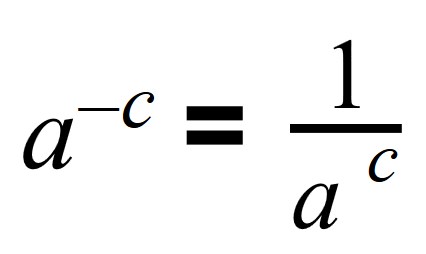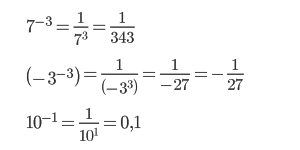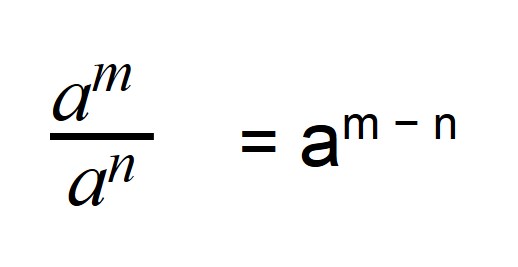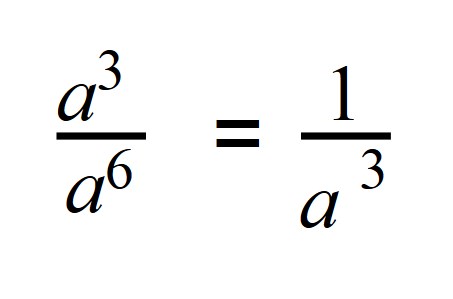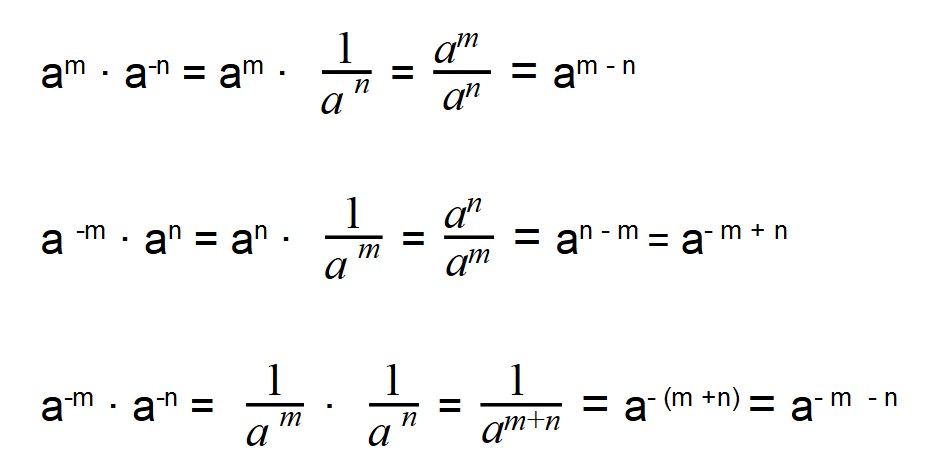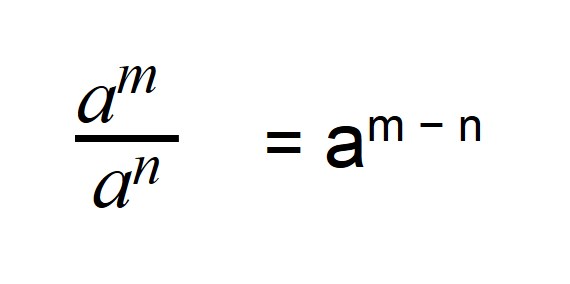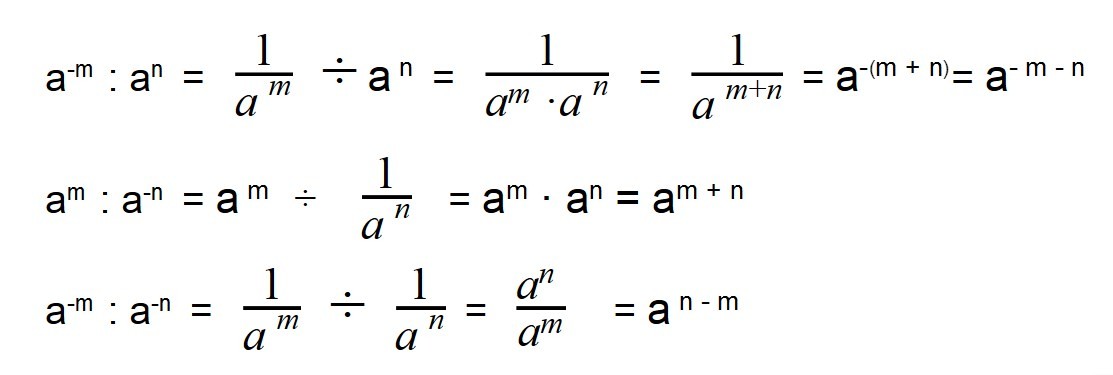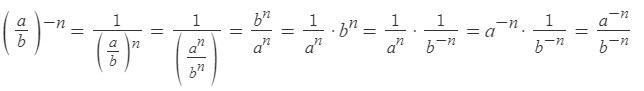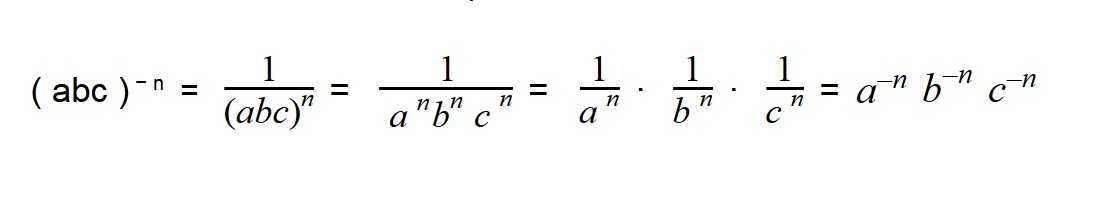Что означает первая степень
Степени тугоухости и их особенности
Полезные статьи и актуальная информация от специалистов по слуху «Аудионика»
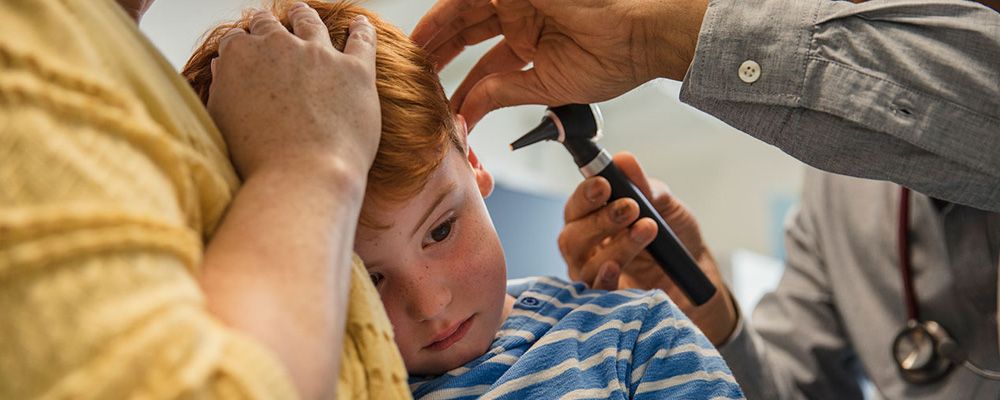
Тугоухость может развиваться медленно или проявляет себя остро после травмы, инфекционного или другого заболевания. У большинства пациентов снижение слуха происходит постепенно, так что средний срок от первых симптомов до визита к врачу составляет 8-9 лет. К сожалению, поздняя диагностика тугоухости уменьшает шансы на успешную реабилитацию и возвращение к привычной жизни.
Описывая ту или иную степень снижения слуха, специалисты говорят не только о результатах инструментальных исследований, но и о степени ограничения человека, возможности получения инвалидности.
Классификация нарушений слуха
В основу классификаций потери слуха положены следующие принципы:
По типу поражения выделяют кондуктивную, нейросенсорную или смешанную тугоухость. При кондуктивной снижение происходит в результате патологии проведения звуковой волны (пороки формирования органа, травмы, воспаления или инфекции наружного, среднего уха). Нейросенсорная тугоухость возникает при патологии внутреннего уха, нерва или коры больших полушарий мозга. Среди причин хромосомные аномалии, инфекции, алкоголизм матери при вынашивании беременности, травмы, опухоли, аутоиммунные процессы, возрастные изменения. Смешанный тип включает оба поражения.
По времени возникновения различают врожденные и приобретенные случаи патологии.
Симптомы могут появиться остро (например, после приема препаратов), и тогда тугоухость называют внезапной. Если состояние усугубляется с течением времени, диагностируют прогрессирующую тугоухость.
Если изменения развиваются синхронно на обоих ушах, говорят о симметричной тугоухости, в противном случае – об асимметричной.
Сурдологи выделяют 4 степени нарушения слуха:
Диагностическими критериями являются данные аудиограммы, степень влияния на обычное функционирование. Здоровый человек воспринимает звуки интенсивностью от 20 до 20000 Дб и распознает сигналы высокой, низкой частоты. О тугоухости говорят тогда, когда больной перестает воспринимать сигналы, чья интенсивность находится в интервале от 20 Дб. Степени нейросенсорной тугоухости имеют те же основные характеристики, что и при кондуктивной. Разница заключается в снижении разборчивости по звукам разной частоты.
Классификация нарушений слуха слабо связана с определением инвалидности, так как основаниями для назначения пособия становятся:
При оценке степени утраты трудоспособности эксперты ориентируются на показатели того уха, которое лучше слышит и часто «снимают» инвалидность при овладении навыками жестового языка или чтения по губам. Они объясняют, какой степени бывает потеря слуха, при которой можно претендовать на пособия по инвалидности. Так при тяжелых или глубоких нарушениях человек могут дать 2 или 3 группу инвалидности. 1 группа назначается только лицам, имеющим другие тяжелые заболевания.
Легкая потеря слуха (1 степень тугоухости)
Пациенты с таким нарушением слуха не торопятся к врачу. Они перестают обращать внимание на тихие фоновые звуки: пение птиц, тиканье часов, удары капель воды. Люди отмечают неудобство в распознавании шепотной речи или с трудом беседуют в шумном помещении. По данным обследования диагностическими критериями этой степени считают:
Такая степень часто не мешает справляться с производственными обязанностями, бытовыми вопросами.
Умеренные нарушения дают понять пациенту с тугоухостью, что у него появились определенные сложности с восприятием звуковой информации. Он может не расслышать звонок телефона, шум офисной техники. В быту или на работе такой человек станет чаще переспрашивать собеседников. А если кто-то обратится к нему в шумном помещении, то пациент с тугоухостью просто не услышит речь.
Умеренную степень диагностируют при следующих результатах исследования:
Тяжелая потеря слуха (3 степень тугоухости)
Скрыть от себя или окружающих тяжелую степень нарушения слуха не получится. Человек с такой тугоухостью может слышать обращенную речь лишь на близком расстоянии, если собеседник произносит слова четко и громко. Он воспринимает обычные звуки большого города – крики, гудки автомобилей, производственный шум. Но коллективная беседа на совещании, разговор по телефону уже вызывают затруднения.
Тяжелая тугоухость может стать основанием для оформления 3 группы инвалидности. Для нее характерны следующие параметры:
Глубокая потеря слуха (4 степень тугоухости)
При такой степени нарушения общение без слухового аппарата невозможно. Человек слышит только крик с малого расстояния, не может поговорить по телефону. Без усиления он воспринимает лишь самые громкие звуки из внешней среды, например, шум самолета, отбойный молоток, концерт рок-музыки.
Глухота
Под глухотой понимают либо полное отсутствие слуха, либо такое выраженное снижение, при котором человек не понимает обращенную речь, а порог восприятия превышает 91 Дб. Абсолютная глухота – редкое явление. Чаще у такого пациента сохраняется восприятие звуков, произнесенных рядом с ушной раковиной, но сложить из них слова он не в состоянии. Именно этот признак позволяет отличить тугоухость 4 степени от глухонемоты, хоты сурдологи признаются, что такая граница весьма условна.
Возникновение глухоты до того, как ребенок начнет говорить, приводит к формированию глухонемоты.
Сводная таблица потери слуха
Краткая информация о степенях нарушения слуха представлена в таблице.
| Степень снижения | Значения порогов слуха на стандартных частотах (в Дб) | На каком расстоянии человек воспринимает разговорную речь | На каком расстоянии человек воспринимает шепот |
|---|---|---|---|
| Здоровый человек | 0-25 | Более 10 м | 6 м |
| 1 | 26-40 | От 6 до 3 м | От 2 м – до ушной раковины |
| 2 | 41-55 | От 3 м и менее | Рядом с ухом |
| 3 | 56-70 | Громко рядом с ушной раковиной | Восприятие невозможно |
| 4 | 71-90 | Только громкий крик рядом с ушной раковиной | Восприятие невозможно |
| глухота | Более 90 | Восприятие невозможно | Восприятие невозможно |
Исправникова Олеся Владимировна
Обладатель диплома МГПУ по специальности «Сурдоакустик». Специалист по слуху «Аудионика» с 2016 года
Свойства степеней. Действия со степенями
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).
Отрицательная степень
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 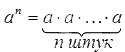
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).
Ожирение 1 степени
Ожирение — хроническое нарушение обмена веществ, которое может возникнуть у мужчин и женщин в любом возрасте. Под ожирением понимают увеличение массы тела за счет чрезмерного образования жира и отложения его в организме.
Сегодня ожирение — это не просто медицинская патология, но и одна из важных социальных проблем: по данным ВОЗ, 39% взрослых страдают от избыточного веса, а у 13% есть та или иная степень ожирения. Это заболевание существенно ухудшает качество жизни людей, снижает работоспособность и общую продолжительность жизни пациентов.
Степени ожирения
Существует несколько классификаций ожирения, но для бытового понимания удобнее всего распределение по степеням — то есть, насколько текущий вес человека отклонён от идеального. Под идеальным весом подразумевают соответствие ИМТ (индекс массы тела) показателям гармоничного сочетания роста и веса. Он рассчитывается по формуле:
ИМТ = вес / (рост в метрах) 2
Например: вес человека — 92 кг, рост 1,65 м. Квадрат роста — 2,7225. Отсюда ИМТ: 92/2,7225=33,8.
В зависимости от ИМТ дается оценка весу пациента:
В приведенном выше примере имеется ожирение первой степени.
Причины ожирения первой степени
В основе ожирения первой степени лежит, как правило, снижение физической активности при сохранении прежнего рациона питания. Человек привык к определенной пище, она насыщает его. При этом по какой-то причине он стал меньше двигаться или уменьшилась скорость обменных процессов. Нутриенты (питательные вещества) поступают, как и ранее, а их расходование сократилось. В таком случае излишки начинают откладываться в организме в виде жира.
Нужно обязательно искать причину, по которой запустился процесс откладывания жира. При ожирении 1 степени это могут быть:
Симптомы ожирения начальной стадии
Чаще всего ожирение 1 степени рассматривается как косметическая проблема. Каких-то выраженных патологических признаков пациент не отмечает или они проявляются при каких-то определенных условиях. Например:
Ожирение первой степени может быть стабильным или прогрессирующим. Первое означает, что, повысившись по какой-то причине, вес более не растет, но и не снижается. Чаще всего это случается по каким-то болезненным причинам, но человек при этом поддерживает прежнюю физическую активность. Отложившийся жир остается, а новый не накапливается, потому что человек держит баланс между поступлением и расходованием питательных веществ.
Прогрессирующее ожирение постепенно (с разной скоростью у разных людей) переходит во 2-ую и последующие стадии.
Лечение ожирения 1 степени
Лечить ожирение 1 степени должен врач. Чтобы выявить причины заболевания, нужно не только оценить ИМТ, но и пройти обследование, в которое входят:
По результатам обследования эндокринолог или диетолог смогут оценить риск развития связанных с ожирением патологий — гипертонии, заболеваний сердца, суставов, жирового перерождения печени и т. д. Врач подберет адекватную схему лечения ожирения первой степени, которая состоит из нескольких взаимосвязанных процессов.
Немедикаментозное лечение ожирения 1 степени
Медикаментозное лечение ожирения первой степени
Хирургическое лечение ожирения
Использование методов быстрого похудения, рекламируемых различными «школами» и самоучками-нутрициологами, самостоятельная коррекция диеты чреваты усугублением проблемы. Появление быстрого результата не является показателем качественного избавления от лишнего веса. Чем резче человек худеет, тем быстрее снижается уровень лептина — гормона, регулирующего энергетические процессы и снижающего аппетит. Через некоторое время уровень лептина снова повысится, что может привести к перееданию и повторному набору массы тела.
Получить консультацию врача и пройти обследование вы можете у врача-диетолога и врача-бариатрического хирурга ФНКЦ ФМБА. Записаться на прием можно через специальную форму на сайте или по телефону.