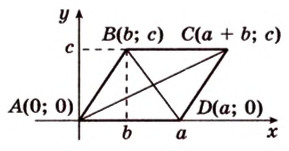
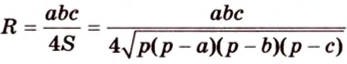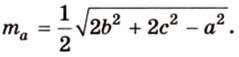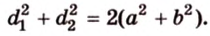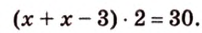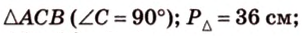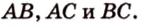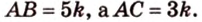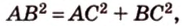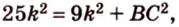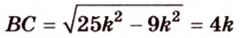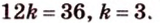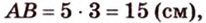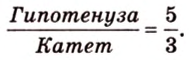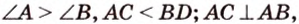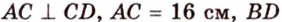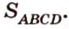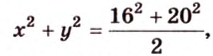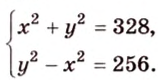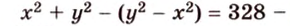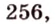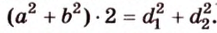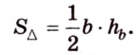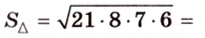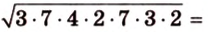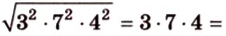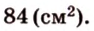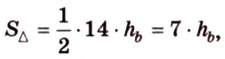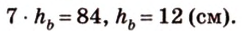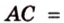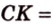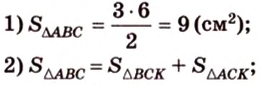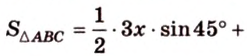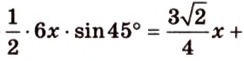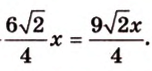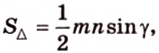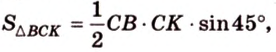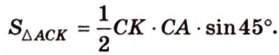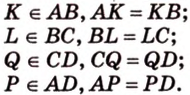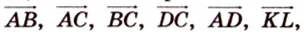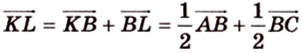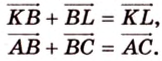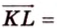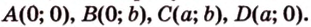Что означает планиметрия и стереометрия
Индивидуальный исследовательский проект по математике на тему: «Стереометрия и планиметрия, сходства и различия» выполнен студенткой группы 1 НК Пикаловой Ольгой
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
ПАВЛОВСКИЙ ФИЛИАЛ ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАТЕЛЬНОГО УЧЕРЕЖДЕНИЯ ВОРОНЕЖСКОЙ ОБЛАСТИ
«ГУБЕРНСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ»
по учебному предмету «Математика»
«СТЕРЕОМЕТРИЯ И ПЛАНИМЕТРИЯ, СХОДСТВА И РАЗЛИЧИЯ»
студентка группы 1 НК
Пикалова Ольга Васильевна
преподаватель математики, ВВК
Данилова Любовь Александровна
1.2. История происхождения стереометрии………………………………….…. 5
1.3. Основные аксиомы и теоремы стереометрии……………………………… …6
1.4. Планиметрия. История происхождения планиметрии……………..………..8
1.5. Важные факты о планиметрии……………………………………………….11
Глава II Сходства и различия планиметрии и стереометрии в жизни…………..15
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Планиметрия – это раздел геометрии, изучающий двумерные фигуры, то есть фигуры, которые можно расположить в одной плоскости.
Мы считаем, что данная тема актуальна всегда, так как каждый человек проходящий школьный курс или же в колледже, изучает эти два раздела. Стереометрия и планиметрия позволяет нашему воображению развиваться, строить разные фигуры на плоскости или представлять фигуры в пространстве.
Объект исследования – на студентов группы 1 НК, в которой проведена интеллектуальная игра.
Предмет исследования – стереометрия и планиметрия, сходства и различия. Цель исследования – выяснить, в чем же сходства и различия между разделами геометрии такими как планиметрия и стереометрия.
1. Рассмотреть понятия: стереометрии, планиметрии,
2. Изучить историю происхождения стереометрии и планиметрии,
3. Исследовать основы стереометрии и планиметрии,
4. Подобрать примеры из жизни
5. Разработать задания для игры «Знаешь ли ты стереометрию?»
Методы исследования: теоретическое, математическое.
Таким образом, в ходе нашего исследования мы пришли к выводу, что стереометрия и планиметрия могут обладать не только сходствами, но и различиями, которые мы рассмотрели в следующих главах.
Глава I . Планиметрия и стереометрия
Основными и простейшими фигурами в пространстве являются: точки, прямые и плоскости. Наряду с этими фигурами есть еще геометрические тела, которые окружают нас в жизни, где бы мы ни были. Так, например, кристаллы имеют форму геометрических тел, поверхности которых составлены из многоугольников. Такие поверхности называются многогранниками. [3;6]
Самый простой многогранник – это куб. Капли жидкости в невесомости принимают форму геометрического тела, называемого шаром. Такую же форму имеет волейбольный мяч, мандарин и многое другое. Консервная банка имеет форму геометрического тела, называемого цилиндром.
В отличии от реальных предметов геометрические тела, как и всякие геометрическое фигуры, являются воображаемыми объектами. Мы представляем геометрическое тело как часть пространства, отделенную от остальной части пространства поверхностью – границей этого тела. Так, например, граница шара есть сфер, а граница цилиндра состоит из двух кругов – оснований цилиндра и боковой поверхности.
1.2. История происхождения стереометрии.
Геометрия зародилась в древнем Египте около двух тысяч лет до н.э. писал древнегреческий учёный Геродот. При строительстве даже самых примитивных сооружений необходимо было рассчитать сколько материала пойдёт на постройку, уметь вычислять расстояние между точками в пространстве и углы между прямыми и плоскостями, знать свойства простейших геометрических фигур. Так, египетские пирамиды, сооружённые за 2-4 тысячелетия до н.э., поражают точностью своих метрических соотношений, свидетельствующих, что строители уже знали многие стереометрические положения и расчёты.
Развитие торговли и мореплавания требовало умений ориентироваться во времени и пространстве. Начиная с 7 в. до н.э. в древней Греции создаются философские школы, в которых происходит постепенный переход от практической к теоретической геометрии. Одной из самых первых и известных школ была пифагорейская, названная в честь своего основателя. Для своих философских теорий пифагорейцы использовали правильные многогранники. Их форму придавали элементам первооснов бытия, а именно огонь – тетраэдр, земля – гексаэдр (куб), воздух – октаэдр, вода – икосаэдр. Название многогранников также древнегреческое происхождение, в них зашифровано число граней. [6;14]
По мнению древних Вселенная имела форму правильного додекаэдра, и мы живём внутри небесного свода, имеющего форму поверхности правильного додекаэдра. Более поздняя философская школа- Александрийская – дала миру знаменитого учёного Евклида, который жил около 3000 лет до н.э. Им была написана знаменитая книга «Начала», по которой учились 2000 лет. В «Началах» Евклида было представлено стройное аксиометрическое строение геометрии.
Знания по стереометрии применяются в различных науках: в астрономии при изучении планет и их свойств, в физике, исследуя структуру молекул и атомов, имеющих форму шара и др. очень многие «беды» начинающих изучать стереометрию происходят от неумения сделать правильный и удобный для решения задачи рисунок, или чертёж. Причём говорим сейчас не об аккуратности, а о смысловой нагрузке чертежа. Чертёж в стереометрии резко отличается от чертежа в планиметрии. В планиметрии чертёж точно соответствует условию теоремы или данным задачи, в стереометрии, при изображении пространственных фигур на плоскости, наблюдается другая картина, чем в планиметрии, например, как изобразить куб.
В 7-9-х классах на уроках алгебры и в учебниках проблема пространственного воображения считается чужой, а в курсе геометрии всё внимание сосредотачивается на двухмерных объектах и учащимся не предоставляется возможность работать с пространственными объектами, развивая своё воображение, на первых же уроках стереометрии мы сталкиваемся с проблемами: пространственное мышление учеников не развито; они не умеют читать изображения пространственных тел, не умеют их изображать.
Благоприятное время для начала развития пространственного мышления это 5-6 классы средней школы. Поэтому, хоть и медленно, на уроки математики в этих классах проникают специальные упражнения, направленные на его развитие. Затем в 7-9-х классах эта проблема забывается и всплывает (по необходимости) в 10-м классе, поскольку явно даёт о себе знать. В 7-9 –х классах можно выполнять упражнения, которые направлены на формирование у учащихся умений читать изображение пространственных фигур, приучают их вносить мысленные изменения в восприятие, подготавливают к обучению в 10-м классе. [6;21]
1.3. Основные аксиомы и теоремы стереометрии
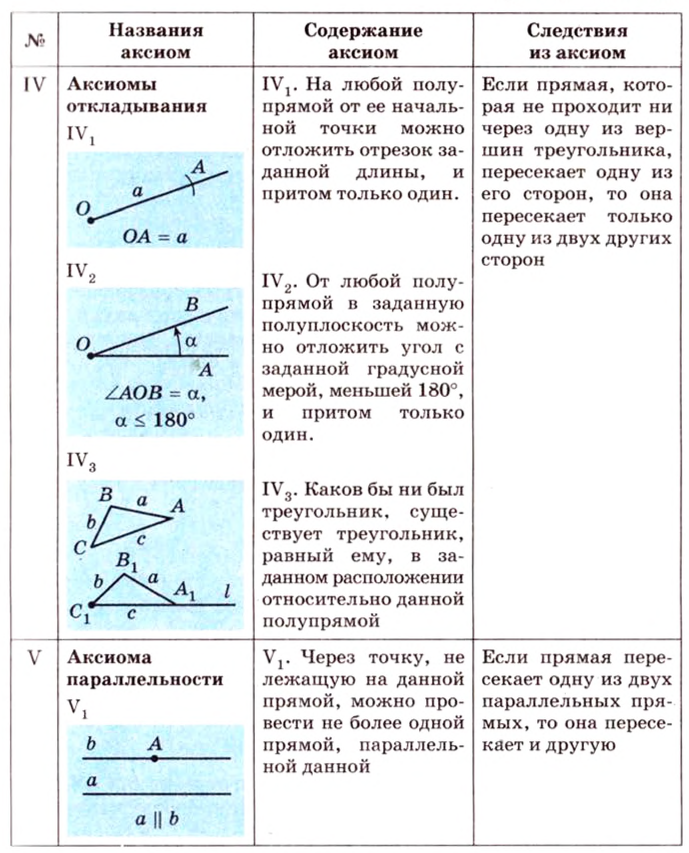
Аксиомы в стереометрии, рассмотрим по порядку:
· Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
· Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.
· Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.
· Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.
Основные теоремы стереометрии:
Теоремы о параллельности прямых и плоскостей
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут: a // β
Теорема 1: Если прямая AB параллельна какой-нибудь прямой CD, расположенной в плоскости P, то она параллельна самой плоскости.
Теорема 2: Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.
Теорема 3: Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.
Теорема 4: Если две пересекающиеся прямые AB и DC одной плоскости соответственно параллельны двум прямым A1 B1 и C1 D1 другой плоскости, то эти плоскости параллельны. [5;8]
Теоремы о перпендикулярности прямых и плоскостей
Теорема 1: Для того что бы прямая AB была перпендикулярна плоскости P, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости.
Теорема 2: Для того, чтобы прямая DE проведенная на плоскости P через основание наклонной AC была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции BC, наклонной на плоскость P.
Теорема 3: Если две прямые AB и CD перпендикулярны одной плоскости P, то они параллельны между собой.
Теорема 4: Если две плоскости P и Q перпендикулярны одной прямой AB, то они параллельны друг другу.
1.4. Планиметрия. История происхождения планиметрии.
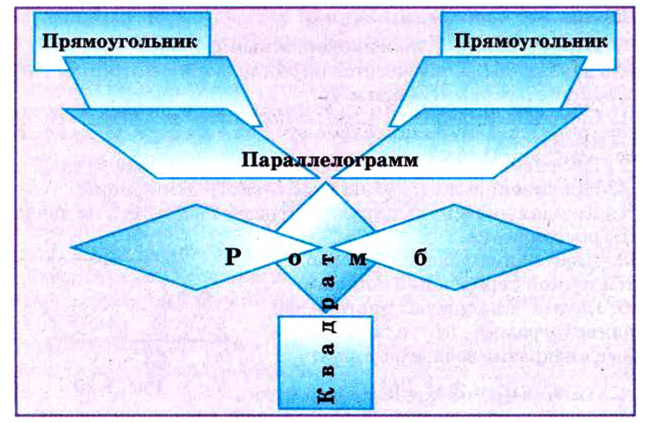
§ Параллелограмм (частные случаи Квадрат, Прямоугольник, Ромб)
Первый дошедший до нас полный трактат по геометрии, представляющий собрание и систематизацию открытий греческих математиков, принадлежит знаменитому александрийскому геометру Эвклиду. Это бессмертное сочинение носит название «Начала» и представляет полный курс так называемой элементарной геометрии, имеющий, за весьма немногими исключениями, объем, в котором геометрия входит в настоящее время в круг преподавания средних учебных заведений. ( Приложение 2 ) [2;6]
Новинкой этого трактата является метода доказательства, состоящая в доказательстве абсурдности противоположного. В нем автор обнаруживает образцовую последовательность изложения и строгость доказательств. Известен анекдот о Птолемее (Лаге), желавшем познакомиться с геометрией, но упрекавшем Эвклида за длинноту изложения, на что геометр отвечал словами: «в математике нет царской дороги». Возможность события вероятна, ибо Птолемей, как начинающий, мог не видеть, что краткость изложения не всегда безопасна для строгости доказательства.
Кроме «Начал», Эвклидом написаны были несколько других работ, которые не дошли до нас; из этих работ наибольшей глубиной мысли отличается трактат под заглавием «Поризмы». Об этом трактате мы знаем лишь по неясным указаниям александрийского математика Паппуса. Некоторые из выдающихся геометров последних веков обратили свою пытливость к восстановлению и уяснению содержания этого трактата по темным намекам Паппуса.
Эти работы дали толчок к развитию новых приемов в геометрии, составляющих предмет так называемой проективной геометрией. Проективная геометрия рассматривает фигуры как перспективу или проекцию других фигур. При таком рассмотрении некоторые свойства фигур сохраняются в их перспективе, некоторые же теряются. Теряются так называемые метрические свойства, а именно перспектива меняет величину углов, а также относительные размеры частей фигур. Так, например, круг в перспективе обращается в эллипс.
Те же свойства фигур, которые сохраняются в перспективе, носят название проективных свойств фигур и составляют предмет изучения проективной геометрии. Так, например, касательная к кругу в перспективе остается касательной к эллипсу.
Под последним названием разумеется совокупность предложений, дающих числовые соотношения между геометрическими величинами, входящими в вопрос, в отличие от геометрического положения, рассматривающего свойства фигур, зависящие от их положения, но не зависящие от размеров этих фигур.
Перечисляя открытия Архимеда в геометрии, прежде всего надо остановиться на его изысканиях отношения окружности к диаметру, причем для несоизмеримого числа, выражающего это отношение, дано было первое приближение 22/7. Квадратура параболы представляет первый пример на измерение площадей, ограниченных кривыми линиями. Свойства спиралей, теорема о шаре и цилиндре, объемы сфероидов и коноидов суть главнейшие изобретения творческого гения, которому статика обязана столько же, как и геометрии.
Сочинения Аполлония относятся к геометрической форме. Главнейшей работой, давшей автору известность, был трактат о конических сечениях. Здесь мы имеем полную теорию трех линий, эллипса, гиперболы и параболы, носящих общее название конических сечений, свойства их сопряженных диаметров, асимптот, фокусов, нормалей, теорема о поляре, первое понятие об эволютах и ряд прекрасных вопросов на maxima и minima.
Теорию эпициклов, играющую роль в Птолемеевой системе мира, приписывают тоже Аполлонию. Последователи Архимеда и Аполлония направили свои изыскания на астрономию и на части геометрии, имеющие связь с этой наукой. [6;32]
Сюда относятся работы Гиппарха и Птолемея. В этих работах, а также в «Сфериках» Менелая мы находим прямолинейную и сферическую тригонометрии древних греков. Этот период александрийской школы есть уже период упадка геометрии; кроме указанных астрономов, мы встречаем тут лишь комментаторов, из которых по праву приобрел наибольшую известность Паппус.
Сочинение Паппуса, носящее заглавие «Collectanea mathematica», драгоценно как источник для знакомства с состоянием геометрии в Греции, ибо большинство сочинений древних геометров, как известно, не дошло до нас. В работах Паппуса мы встречаем известную теорему Гюльдена, зародыш учения об ангармонии и инволюции и свойства шестиугольника, вписанного в коническое сечение.
Вот краткий исторический обзор главнейших работ греков по геометрии. Они делили геометрию на три части: на элементы, прикладную геометрию, или геодезию, и высшую геометрию, которая представляла совокупность решений вопросов и теорий, в коих геометр мог найти необходимые указания для доказательства теорем и решения задач. Эту последнюю часть новейшие математики называют геометрическим анализом древних греков.
1.5. Важные факты о планиметрии
Среди всего прочего стоит выделить точку и прямую. Они являются двумя основными понятиями планиметрии. [ 9;8]
· Угол, который состоит из двух лучей, выходящих из одной точки.
В планиметрии это наиважнейшие правила, по которым работает вся наука. Да и не только в ней. По определению, речь идет об утверждениях, не требующих доказательств.
Аксиомы, которые буду рассмотрены ниже, входят в так называемую Евклидовую геометрию.
· Есть две точки. Через них всегда можно провести единственную прямую.
· Если существует прямая, то есть точки, которые на ней лежат, и точки, не лежащие на ней.
Это 2 утверждения принято называть аксиомами принадлежности, а следующие – порядка:
· Если на прямой расположены три точки, то одна из них обязательно находится между двумя другими.
· Плоскость делится любой прямой на две части. Когда концы отрезка лежат на одной половине, то значит и весь объект принадлежит ей. В ином случае исходная прямая и отрезок имеют точку пересечения.
· Каждый отрезок имеет длину, отличную от нуля. Если точка разбивает его на несколько частей, то их сумма будет равна полной длине объекта.
· У каждого угла есть определенная градусная мера, которая не равна нулю. Если разбить его лучом, то исходный угол будет равен сумме образованных.
· На плоскости расположена прямая. Через любую точку, не принадлежащую ей, можно провести лишь одну прямую, параллельную данной.
По сторонам (соотношения выплывают из названий):
Два угла независимо от ситуации всегда будут острыми, а третий определяется первой частью слова. То есть у прямоугольного треугольника один из углов равен 90 градусам.
· Чем больше угол, тем больше противоположная ему сторона.
· Всегда можно вписать окружность в треугольник или же описать ее вокруг него.
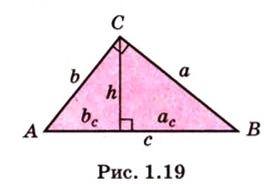
Об одной из основных формул планиметрии говорит теорема Пифагора. Работает она исключительно для прямоугольного треугольника и звучит так: квадрат гипотенузы равен сумме квадратов катетов: AB2 = AC2 + BC2.
Информации на эту тему чрезвычайно много. Ниже приведена лишь самая важная. [ 9;16]
· Сума внутренних углов равна 360 градусам.
Содержание:
Что такое планиметрия
Логическое построение планиметрии можно описать как последовательность следующих этапов.
Для школьного курса планиметрии определены:
К определяемым понятиям в геометрии относят отрезок, луч, треугольник и т. п., поскольку для них существуют объяснения «что это такое?». Определяемых понятий много. Приведем пример.
Аксиомы планиметрии
С целью установления правильности утверждения о свойствах той или иной геометрической фигуры прибегают к некоторым рассуждениям. Среди них есть такие, которые требуют доказательства (теоремы, задачи). Утверждение, истинность которого устанавливается путем доказательства и которое используется для доказательства других утверждений, называют теоремой.
Теорема состоит из: условия и вывода. Для доказательства теорем в школьном курсе геометрии в основном используют следующие методы:
Все рассуждения при доказательстве теорем произвольным методом основываются на аксиомах и известных доказанных фактах. Т.е. чтобы доказать теорему, разрешается пользоваться только основными свойствами простейших фигур (аксиомами) и свойствами, доказанными ранее (теоремами). Никакими другими свойствами фигур, даже если они представляются очевидными, пользоваться нельзя. Например, доказывая теоремы, можно использовать рисунки. Однако это лишь геометрическая модель содержания текста, выраженного словами, поэтому делать по рисунку выводы о свойствах фигур не разрешается.
Итак, геометрия, как и другие математические науки, строится по такой схеме: сначала следует ввести основные понятия, задать аксиомы (правила игры), а потом, опираясь на аксиомы, выводить другие факты (проводить игру по определенным правилам, не противоречащим друг другу).
Опорные факты курса планиметрии
Данный параграф предназначен для повторения курса планиметрии. Необходимость в нем обусловлена тем, что многие вопросы планиметрии на первом этапе обучения в школе рассматриваются несколько поверхностно. В следующих классах уровень изучения материала повышается, а вернуться и углубить пройденное удается не всегда. Поэтому мы систематизируем и обобщим основные сведения по планиметрии, условно разбив их на блоки: взаимное расположение прямых на плоскости; окружность и круг; многоугольники; треугольник и его элементы; выпуклые четырехугольники.
Взаимное расположение прямых на плоскости
Расстоянием от точки 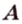
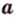
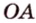
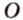
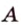
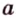
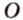
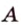
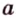
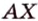
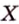
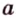
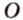
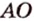
Две различные прямые 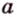
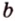
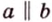
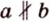
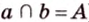
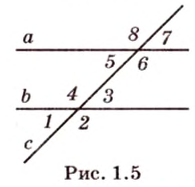
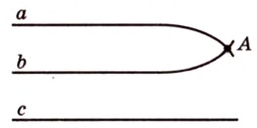
Вследствие пересечения двух прямых третьей прямой образуется восемь углов (рис. 1.5) (прямые а и Ь могут пересекаться, но прямая с через точку их пересечения не проходит):
Признаки параллельности прямых:
Окружность и круг
Кругом с центром 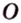
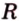
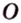
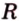
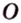
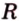
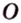
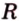
Отрезки, которые соединяют центр с точками окружности и имеют длину 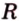
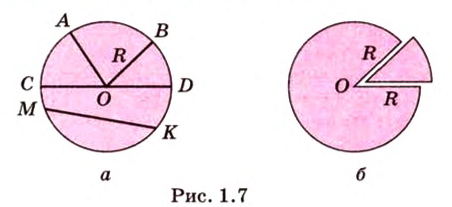
Части круга, на которые он делится двумя радиусами, называют круговыми секторами (рис. 1.7, б).
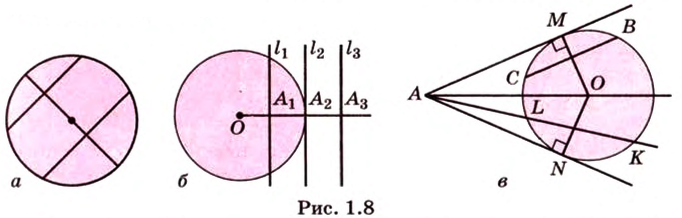
Через три точки, не лежащие на одной прямой, проходит единственная окружность. Диаметр, перпендикулярный к хорде, делит пополам эту хорду и обе дуги, которые стягиваются ею, и наоборот, если диаметр проведен через середину хорды, то он перпендикулярен этой хорде и делит пополам дугу, которую она стягивает (рис. 1.8, а).
Дуги, которые находятся между параллельными хордами, равны между собой. Равные дуги стягиваются равными хордами, и наоборот, равные хорды стягивают равные дуги.
Равные хорды одинаково отдалены от центра, и наоборот, хорды, одинаково отдаленные от центра, равны между собой. Большая из двух хорд меньше отдалена от центра, и наоборот, из двух хорд больше та, которая меньше отдалена от центра (рис. 1.8, а).
Каким может быть взаимное расположение прямой и окружности?
Рассмотрим окружность с центром 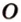
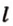
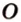
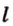
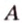
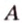
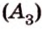
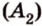
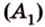
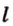
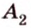
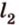
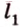
Прямая, проходящая через точку окружности, является касательной к окружности только тогда, когда она перпендикулярна радиусу, проведенному в эту точку. Если касательная параллельна хорде окружности, то точка касания делит пополам дугу, которую стягивает хорда (рис. 1.8, в; 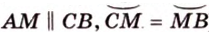
Если из одной точки к окружности проведены две касательные, то отрезки этих касательных (от точек касания до данной точки) равны между собой, а луч, проведенный через данную точку и центр окружности, делит пополам угол между касательными (рис. 1.8, в; 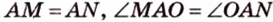
Угол, образованный двумя касательными, называется описанным (рис. 1.8, в; 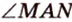
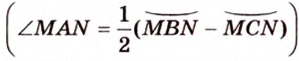
Многоугольники
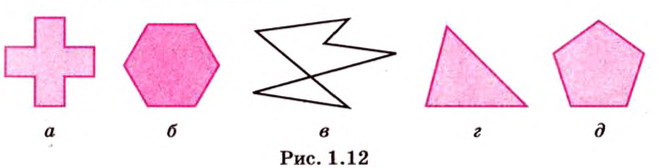
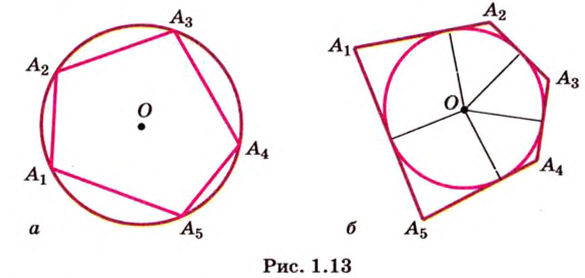
Многоугольник выпуклый, если он лежит в одной полуплоскости относительно каждой прямой, проходящей через две его соседние вершины (рис. 1.12, б, г, д).
Многоугольники называют равными, если при наложении они совмещаются. Для выпуклого 
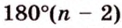

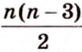

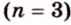
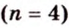
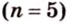
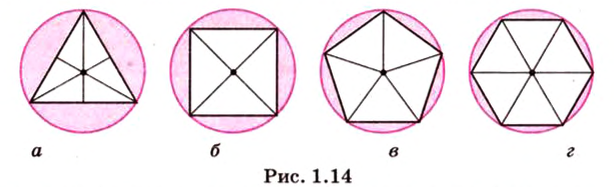
Как построить правильный 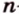
Если окружность разделить на 

Если окружность разделить на 

Вокруг каждого правильного многоугольника можно описать окружность или в каждый правильный многоугольник можно вписать окружность.
В правильном многоугольнике центры описанной и вписанной окружностей совпадают. Общий центр описанной и вписанной окружностей называется центром правильного многоугольника. Радиус вписанной окружности называют апофемой правильного многоугольника.
Угол, образованный двумя радиусами, проведенными через смежные вершины правильного многоугольника, называется его центральным углом. Все центральные углы правильного многоугольника равны между собой и составляют 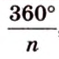

В правильном 

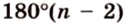
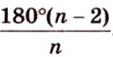
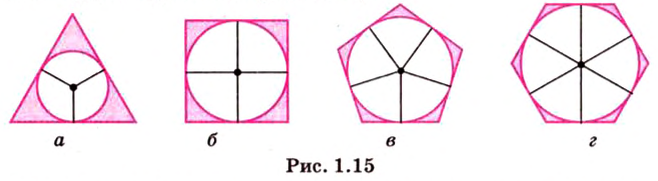
Окружность, вписанная в правильный многоугольник, касается его сторон в их серединах. Центр окружности, вписанной в правильный многоугольник, является точкой пересечения серединных перпендикуляров его сторон (рис. 1.15).
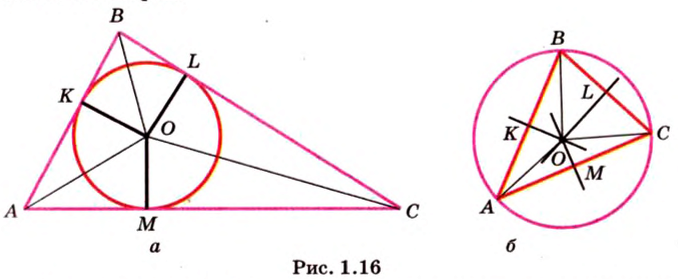
Простейшим многоугольником является треугольник. В любой треугольник можно вписать окружность, причем только одну. На рисунке 1.16, 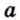

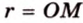
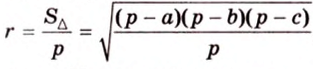
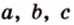
Можно ли в любой четырехугольник вписать окружность?
Ответ. Нельзя. В четырехугольник можно вписать окружность только при условии, что суммы длин его противоположных сторон равны.
Вокруг произвольного треугольника можно описать окружность, притом только одну (см. рис. 1.16, б). Центр окружности, описанной вокруг треугольника, является точкой пересечения серединных перпендикуляров, проведенных к его сторонам. Центр окружности 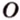
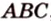
На рисунке 1.16, б изображена окружность с центром 
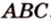
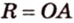
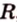
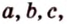
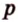
Можно ли описать окружность вокруг произвольного четырехугольника?
Ответ. Нельзя. Вокруг четырехугольника можно описать окружность только тогда, когда суммы противоположных углов равны 180°.
Треугольник и его элементы
Треугольником называется фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки. Рассмотрим 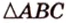
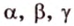
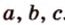
Треугольник называется тупоугольным, прямоугольным или остроугольным, если его наибольший внутренний угол соответственно больше, равен или меньше 90°.
Треугольник называется равнобедренным, если у него две стороны равны (боковые стороны). Основанием равнобедренного треугольника является сторона, которая не равна ни одной из двух других равных сторон.
Треугольник, все стороны которого равны, называется равносторонним, или правильным.
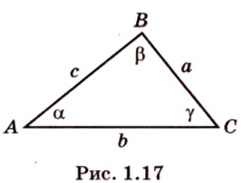
Соотношение между сторонами и углами треугольника:
Треугольник можно определить любой тройкой таких основных элементов: либо двумя сторонами и углом между ними, либо одной стороной и двумя углами, либо тремя сторонами.
Например, 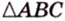
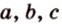
Соотношение между внутренними и внешними углами треугольника: любой внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Из трех отрезков можно образовать треугольник тогда и только тогда, когда любая его сторона меньше суммы и больше разности двух других его сторон. В любом треугольнике можно провести три медианы, три биссектрисы и три высоты.
Свойства биссектрисы угла треугольника: биссектрисы треугольника пересекаются в одной точке, которая лежит в середине треугольника и является центром вписанной
в него окружности.
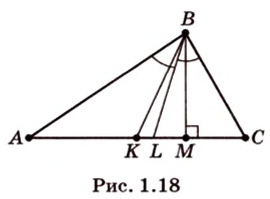
Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим к ней сторонам (рис. 1.18; 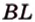
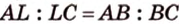
Основные свойства медиан треугольника:
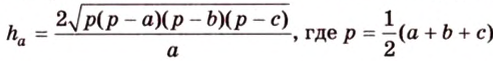
Медиана треугольника 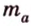
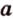
Свойства равнобедренного треугольника: углы при основании треугольника равны; высота, проведенная к основанию, является также биссектрисой и медианой.
Свойства равностороннего треугольника: все углы равны (каждый угол равен 60°); каждая из трех высот является также биссектрисой и медианой; центр окружности, описанной вокруг треугольника, совпадает с центром окружности, вписанной в него.
Стороны прямоугольного треугольника 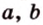
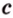
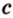
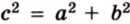
длины гипотенузы равен сумме квадратов длин катетов.
Свойства прямоугольного треугольника:
Выпуклые четырехугольники
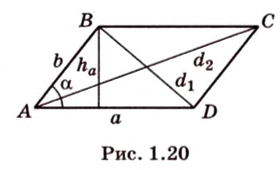
Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом (рис. 1.20).
Если в четырехугольнике исполняется любое из таких условий:
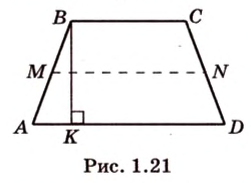
Если боковые стороны трапеции равны между собой, такую трапецию называют равнобокой (рис. 1.21; 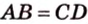
Равнобокая трапеция имеет такие свойства:
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией (рис. 1.21; 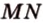
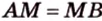
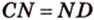
Средняя линия трапеции параллельна ее основаниям и равна их полусумме (рис. 1.21; 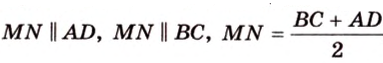
Задачи и методы их решения
Для геометрии закономерным является то, что введенные основные понятия и сформулированная аксиоматика составляют основу для новых утверждений. Однако справедливость последних необходимо доказывать путем определенных рассуждений, основывающихся на ранее доказанных утверждениях или аксиомах. Так формируются математические задачи.
Что такое математическая задача?
Можно ли утверждать, что для успешного решения геометрических задач и доказательства теорем достаточно свободно владеть всем теоретическим материалом?
Нет. Это не так. При хорошем знании теории следует овладеть еще и практическими навыками. А это возможно только в процессе решения задач, начиная с простейших и постепенно переходя к более сложным.
Математические задачи условно разделены на четыре вида, в соответствии с их требованиями: задачи на вычисление, доказательство, исследование и построение. С ними вы уже ознакомились в курсе планиметрии.
Приступая к решению задачи, следует выбрать метод. Методы делят:
Суть синтетического метода заключается в том, что, исходя из условия задачи или теоремы с использованием известных утверждений строится цепочка логических рассуждений, последнее из которых совпадает с требованием задачи. Приведем пример.
Пример №1
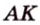
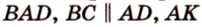
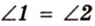
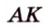
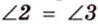
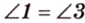
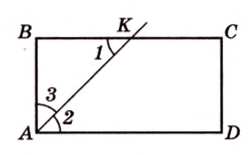
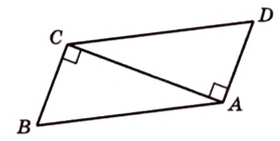
В 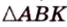
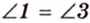
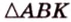
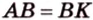
1. Если 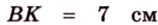
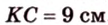
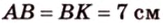
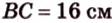
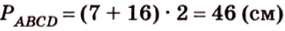
2. Если 
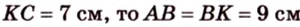
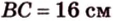
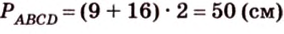
Ответ. 46 см или 50 см.
Эта задача является опорной, поскольку на такой идее строятся многие задачи и для параллелограмма, и для трапеции. У этих фигур биссектриса угла отсекает всегда равнобедренный треугольник.
Отметим, что сокращенное обозначение углов в виде 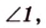
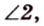
Как видим, в процессе решения задачи 1 используются только известные геометрические утверждения и производятся соответствующие вычисления. Причем для каждой геометрической задачи такие рассуждения свои.
Суть аналитического метода состоит в том, что, исходя из требования (вывода) утверждения (теоремы или задачи) и опираясь на известное утверждение, строится цепочка логических рассуждений, которая показывает, что требование является следствием условия. Приведем пример.
Пример №2
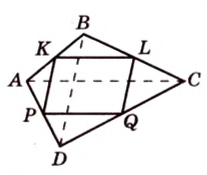
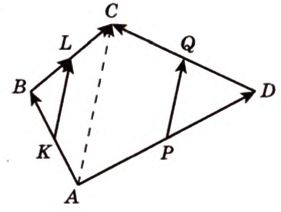
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 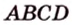

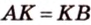
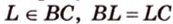

Доказать: 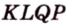
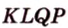
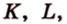
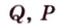
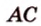
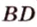
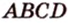
В 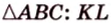
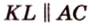
В 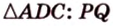

Имеем: 1. 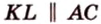
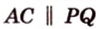
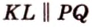
Чтобы решить задачу прямым методом, следует начать с анализа содержания задачи, от которого зависит выбор метода решения. Далее необходимо создать модель в виде рисунка и продолжить рассуждать над каждым действием, которые в совокупности образуют цепочку действий, ведущих либо от условия к требованию, либо от требования к условию.
Суть метода доказательства от противного состоит в том, что, имея утверждение, строим новое, возразив выводу данного. Формулируется утверждение. Исходя из вывода противоположного утверждения, строим цепочку истинных утверждений, пока не получим утверждение, которое противоречит либо условию, либо известной аксиоме или теореме, либо предположению. Таким образом приходим к выводу, что противоположное утверждение ошибочно, а потому исходное является истинным (тут действует логический закон: из двух противоположных утверждений одно истинное, другое ошибочное, третьего не дано). Рассмотрим пример.
Пример №3
Докажите утверждение: если две прямые параллельны третьей, то они параллельны между собой.
Строим противоположное утверждение: существуют две прямые, параллельные третьей и не параллельные между собой.
Математическую задачу считают решенной, если:
Метод от противного называют непрямым методом решения математических задач.
Рассмотрим некоторые другие методы решения геометрических задач, которые делят на виды по использованию математического аппарата.
Алгебраический метод решения задач
Решая задачу алгебраическим методом, следует уделить внимание таким этапам:
Приведем другие примеры решения задач алгебраическим методом.
Пример №4
Периметр прямоугольного треугольника равен 36 см. Гипотенуза относится к катету как 5 : 3. Найдите стороны треугольника.
Дано: 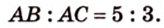
Найти:
Обозначим коэффициент пропорциональности через 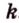
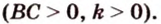
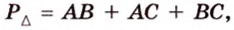
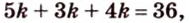
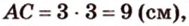
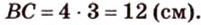
Ответ. 15 см, 9 см и 12 см.
Почему именно так?
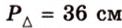
Пример №5
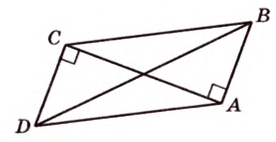
В параллелограмме диагонали равны 16 см и 20 см. Меньшая из них перпендикулярна к его стороне. Найдите площадь этого параллелограмма.
Дано: 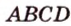
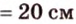
Найти:
Почему именно так?
Пусть 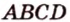
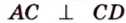
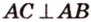
Обозначим стороны параллелограмма: 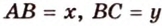
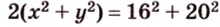
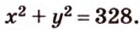
По теореме Пифагора из 
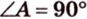
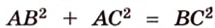
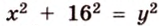
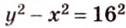
Составим систему уравнений:
Ответ.
В ходе решения этой задачи сначала выбираем формулу для вычисления площади параллелограмма. 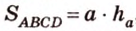
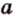
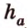
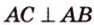
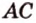
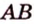
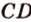
Метод площадей
Пример №6
Стороны треугольника равны 13 см, 14 см и 15 см. Вычислите высоту, проведенную к стороне, которая имеет длину 14 см.
Пусть 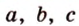
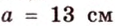
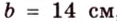
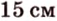
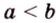
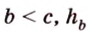
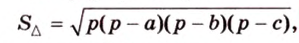
Ответ. 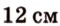
Имея три стороны треугольника 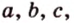
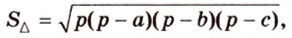
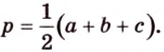
С другой стороны, площадь треугольника можно найти по формулам: 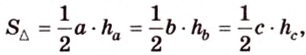
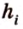

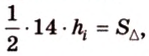
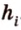
Отметим, что хотя во время решения задачи 6 использовалось алгебраическое уравнение, более существенными в решении этой задачи являются рассуждения о площади фигуры. Поэтому такой метод получил название метод площадей.
Пример №7
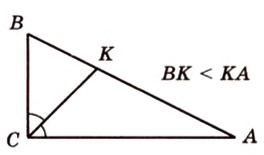
Катеты прямоугольного треугольника равны 3 см и 6 см. Найдите длину биссектрисы прямого угла.
Дано: 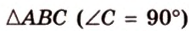
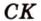
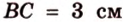
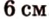
Найти: 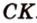
Пусть 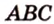
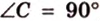
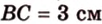
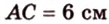
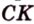
Введем обозначение: 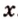
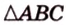
Площадь 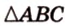
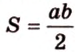
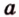
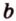
Биссектриса разделила 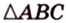
где 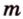
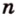
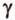
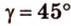
Поскольку 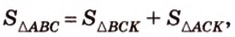
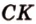
Метод векторов
Чтобы применить метод векторов к решению задачи, необходимо выполнить следующие действия:
Пример №8
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 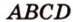
Доказать: 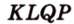
1. Переведем задачу на язык векторов, заменив отрезки векторами: 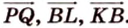
2. Воспользуемся правилом треугольника для сложения векторов: 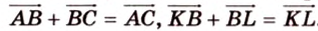
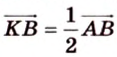
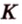
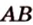
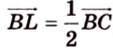
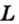
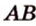
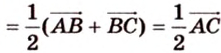
Поэтому 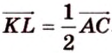
Аналогично 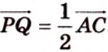
3. Поэтому 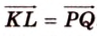
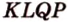
Переведя задачу на язык векторов, получаем требование задачи: доказать равность векторов 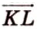
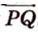
Однако 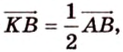
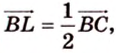
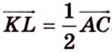
Аналогично получаем, что 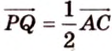
Таким образом, 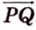
Метод координат
Решая задачу координатным методом, следует выполнить такие действия:
Методом координат чаще всего решают задачи:
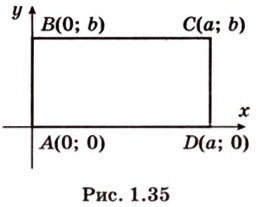
Решая задачу методом координат, необходимо рационально выбрать систему координат: данную фигуру следует разместить относительно осей координат таким образом, чтобы как можно больше координат нужных точек равнялось нулю, а также одному и тому же числу. Например, координаты вершин прямоугольника 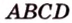
Проиллюстрируем суть метода координат на примере.
Пример №9
Докажите, что когда у параллелограмма диагонали равны, то он прямоугольник.
Разместим параллелограмм в системе координат таким образом, чтобы его вершины имели координаты: 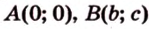
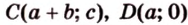
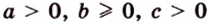
По условию 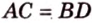
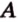
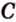
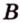
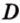
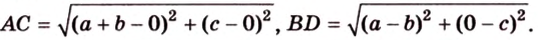
Тогда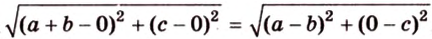
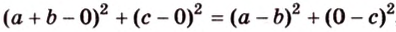
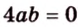
Поскольку 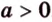
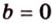
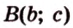
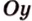
Поэтому угол 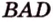
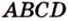
Метод геометрических преобразований: метод поворота, метод симметрии, метод параллельного переноса, метод гомотетии.
Решая задачи методом геометрических преобразований, наряду с данными фигурами рассматривают новые, полученные из данных с помощью определенного преобразования. Выясняют свойства новых фигур, переносят эти свойства на данные фигуры, а затем находят способ решения задачи.
Говорят, что задачи, решенные методами векторов, координат, геометрических преобразований, площадей и другими методами, в которых используется больше свойств геометрических фигур, решены геометрическими методами.
Второй период — формирование геометрии в структурную систему. В VII в. до н.э. центром развития геометрии стала Греция. Древние геометры работали над систематизацией накопленных и новых знаний, устанавливали связи между геометрическими фактами, разрабатывали приемы доказательств. Значительный вклад в развитие математики, в частности геометрии, в этот период сделали Пифагор, Платон, Аристотель, Фалес, Анаксигор, Демокрит, Евклид. В книге «Начала» Евклида сформулированы понятия о фигуре, о геометрическом утверждении и доказательстве. Они остаются актуальными и сегодня.
Особенность начатого Н.И. Лобачевским периода в истории геометрии состоит в том, что после его открытия начали развиваться новые геометрические теории, новые «геометрии» и соответствующие обобщения самого предмета геометрии. В этот период возникло понятие о разновидностях пространства (термин «пространство» в науке может означать как обычное реальное пространство, так и абстрактное, «математическое», пространство). Некоторые теории создавались внутри евклидовой геометрии, как ее особые разделы, а позднее приобретали статус самостоятельных. Другие, подобно геометрии Лобачевского, вводили изменения аксиом и структурировались на основе этих изменений, обобщая и строя науку.
В школьном курсе мы изучаем геометрию Евклида. Перевел труд древнегреческого ученого «Начала» украинский математик Михаил Егорович Ващенко-Захарченко (1825-1912) в 1880 г. На основе этой книги написано множество учебников по геометрии. Например, преподавание геометрии в советской школе почти до 1982 г. осуществлялось по учебнику российского педагога-математика А.П. Киселева (1852-1940). В 1980-х годах украинским математиком А.В. Погореловым было создано новое учебное пособие. Его и сегодня можно найти в библиотеках общеобразовательных учебных заведений.
Современная геометрия является многовекторной и стремительно развивается в совокупностях математических теорий, изучающих различные пространства и их фигуры. Значительный вклад в геометрию сделали и наши соотечественники: М.В. Остроградский, А.М. Астряб, А.П. Киселев, А.Д. Александров, А.Н. Колмогоров, А.В. Погорелов и др.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.