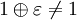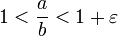Что означает плавающая точка
Числа с плавающей точкой
Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.
Содержание
«Плавающая запятая» и «плавающая точка»
Так как в некоторых, преимущественно англоязычных и англофицированных, странах (см. подробный список Decimal separator (англ.) ) при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (floating point (англ.) ). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия используется термин «плавающая запятая».
Происхождение названия
Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.
Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 8 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123456,78; 8765,43; 123,00 и так далее. В свою очередь, в формате с плавающей запятой (в тех же 8 разрядах) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее.
Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в англ. FLOPS — число операций с плавающей запятой в секунду ),
Структура числа
Число с плавающей запятой состоит из:
Нормальная форма
Использование в вычислительных машинах
Краткий обзор
Существует несколько способов того, как строки из цифр могут представлять числа:
Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как
в нормальной форме представляется в виде
(1,20 × 10 −1 ) × (1,20 × 10 −1 ) = (1,44 × 10 −2 ).
В формате с фиксированной запятой мы бы получили вынужденное округление
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 52 бита + 1 знаковый, показатель — 11 бит. Таким образом получаем диапазон точности примерно от 4,94 × 10 −324 до 1.79 × 10 308 (от 2 −52 × 2 −1022 до
1 × 2 1024 ). Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения бесконечность), получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.
Машинный эпсилон
В отличие от фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел малого порядка и более редкая — для больших чисел. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинного эпсилона.
Машинным эпсилоном называется наименьшее положительное число ε такое, что 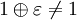

Урок №33. Типы данных с плавающей точкой: float, double и long double
Обновл. 11 Сен 2021 |
Типы данных с плавающей точкой
Есть три типа данных с плавающей точкой: float, double и long double. Язык C++ определяет только их минимальный размер (как и с целочисленными типами). Типы данных с плавающей точкой всегда являются signed (т.е. могут хранить как положительные, так и отрицательные числа).
| Тип | Минимальный размер | Типичный размер | |
| Тип данных с плавающей точкой | float | 4 байта | 4 байта |
| double | 8 байт | 8 байт | |
| long double | 8 байт | 8, 12 или 16 байт |
Объявление переменных разных типов данных с плавающей точкой:
Если нужно использовать целое число с переменной типа с плавающей точкой, то тогда после этого числа нужно поставить разделительную точку и нуль. Это позволяет различать переменные целочисленных типов от переменных типов с плавающей запятой:
Обратите внимание, литералы типа с плавающей точкой по умолчанию относятся к типу double. f в конце числа означает тип float.
Экспоненциальная запись
Обычно, в экспоненциальной записи, в целой части находится только одна цифра, все остальные пишутся после разделительной точки (в дробной части).
На практике экспоненциальная запись может использоваться в операциях присваивания следующим образом:
Разбираемся в числах с плавающей точкой (часть 0)
Здравствуйте, хабровчане. Я давно увлекаюсь темой регистров с плавающей точкой. Меня всегда волновало то, как происходит вывод на экран и т.д. Помню, давным-давно в универе реализовывал свой класс чисел с плавающей точкой, состоящих из 512 бит. Единственное, что я не мог никак реализовать — это вывод на экран.
Как только у меня появилось свободное время, я взялся за старое. Завел себе тетрадку и пошло-поехало. Хотелось додуматься до всего самому, лишь иногда заглядывая в стандарт IEEE 754.
И вот что из всего этого вышло. Интересующихся прошу под кат.
Чтобы освоить эту статью, надо знать следующее: что такое бит, двоичная система, арифметика на уровне знания отрицательных степеней. В статье не будут затронуты инженерные подробности реализации на уровне процессора а также нормализованные и денормализованные числа. Больший упор сделан на перевод числа в двоичную форму и наоборот, а также объяснение того, как вообще хранятся числа с плавающей точкой в виде битов.
Числа с плавающей точкой — очень мощный инструмент, которым надо уметь правильно пользоваться. Они не столь банальны, как целочисленные регистры, но и не столь сложны, если в них грамотно и потихоньку вникнуть.
В сегодняшней статье для примера я буду использовать 32-битные регистры. Числа с двойной точностью (64-битные) работают абсолютно по той же логике.
Сначала поговорим о том, как хранятся числа с плавающей точкой. Старший 31 бит у нас знаковый. Единичка значит, что число отрицательное, а ноль, соответственно наоборот. Далее идут 8 бит экспоненты. Эти 8 битов представляют из себя обычное беззнаковое число. И в самом конце идут 23 бита мантиссы. Для удобства будем обозначать знак как S, экспоненту как E, а мантиссу, как ни странно, M.
Получаем общую формулу
У мантиссы принято считать один неявный единичный бит. То есть мантисса будет представлять из себя 24 бита, но так как старший 23-й бит всегда единица, то его можно не записывать. Таким образом это «ограничение» будет давать нам единственность представления любого числа.
Мантисса из себя представляет обычное двоичное число, но в отличие от целых чисел, старший бит это 2^0 степени и далее по убыванию степеней. Вот тут и пригождается экспонента. В зависимости от ее значения, степень двойки старшего бита увеличивается либо уменьшается. Вот и вся гениальность этой задумки.
Давайте попробуем показать это на наглядном примере:
Представим число 3.625 в двоичном виде. Поначалу разобьем это число на степени двойки.
Степень старшей двойки равна единице. E – 127 = 1. E = 128.
0 1000000 11010000000000000000000
Вот и все наше число.
Попробуем также и в обратную сторону. Пусть у нас есть 32 бита, произвольные 32 бита.
0 10000100 (1)11011100101000000000000
В скобочках указан тот самый неявный старший бит.
Сначала вычислим экспоненту. E = 132. Соответственно степень старшей двойки будет равна 5. Итого имеем следующее число:
Нетрудно догадаться, что мы можем хранить всего лишь диапазон из 24-х степеней двойки. Соответственно, если два числа отличаются в экспоненте на больше чем 24, то при сложении число остается равным большему среди них.
Для удобной конвертации я накидал небольшую программу на языке C.
Шагом сетки является минимальная разницу между двумя соседними числами с плавающей точкой. Если представить последовательность битов такого числа как обычное целое число, то соседнее число с плавающей точкой будет отличаться в битах как целое число на единицу.
Можно выразиться иначе. Два соседних числа с плавающей точкой будут отличаться на 2 ^ (E — 127 — 23). То есть на разницу, равную значению младшего бита.
В качестве доказательства можете поменять main в коде и скомпилировать еще раз.
Думаю на сегодня можно закругляться, а то получается слишком длинно. В следующий раз буду писать о сложении чисел с плавающей точкой и потере точности при округлении.
Плавающая запятая
Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.
Содержание
«Плавающая запятая» и «плавающая точка»
Так как в некоторых, преимущественно англоязычных и англофицированных, странах (см. подробный список Decimal separator (англ.) ) при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (floating point (англ.) ). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия используется термин «плавающая запятая».
Происхождение названия
Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.
Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 8 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123456,78; 8765,43; 123,00 и так далее. В свою очередь, в формате с плавающей запятой (в тех же 8 разрядах) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее.
Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в англ. FLOPS — число операций с плавающей запятой в секунду ),
Структура числа
Число с плавающей запятой состоит из:
Нормальная форма
Использование в вычислительных машинах
Краткий обзор
Существует несколько способов того, как строки из цифр могут представлять числа:
Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как
в нормальной форме представляется в виде
(1,20 × 10 −1 ) × (1,20 × 10 −1 ) = (1,44 × 10 −2 ).
В формате с фиксированной запятой мы бы получили вынужденное округление
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 52 бита + 1 знаковый, показатель — 11 бит. Таким образом получаем диапазон точности примерно от 4,94 × 10 −324 до 1.79 × 10 308 (от 2 −52 × 2 −1022 до
1 × 2 1024 ). Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения бесконечность), получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.
Машинный эпсилон
В отличие от фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел малого порядка и более редкая — для больших чисел. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинного эпсилона.
Машинным эпсилоном называется наименьшее положительное число ε такое, что 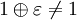

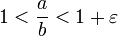
Плавающая точка
Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.
Содержание
«Плавающая запятая» и «плавающая точка»
Так как в некоторых, преимущественно англоязычных и англофицированных, странах (см. подробный список Decimal separator (англ.) ) при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (floating point (англ.) ). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия используется термин «плавающая запятая».
Происхождение названия
Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.
Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 8 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123456,78; 8765,43; 123,00 и так далее. В свою очередь, в формате с плавающей запятой (в тех же 8 разрядах) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее.
Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в англ. FLOPS — число операций с плавающей запятой в секунду ),
Структура числа
Число с плавающей запятой состоит из:
Нормальная форма
Использование в вычислительных машинах
Краткий обзор
Существует несколько способов того, как строки из цифр могут представлять числа:
Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как
в нормальной форме представляется в виде
(1,20 × 10 −1 ) × (1,20 × 10 −1 ) = (1,44 × 10 −2 ).
В формате с фиксированной запятой мы бы получили вынужденное округление
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 52 бита + 1 знаковый, показатель — 11 бит. Таким образом получаем диапазон точности примерно от 4,94 × 10 −324 до 1.79 × 10 308 (от 2 −52 × 2 −1022 до
1 × 2 1024 ). Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения бесконечность), получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.
Машинный эпсилон
В отличие от фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел малого порядка и более редкая — для больших чисел. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинного эпсилона.
Машинным эпсилоном называется наименьшее положительное число ε такое, что