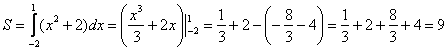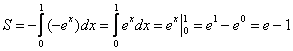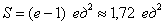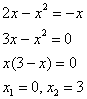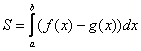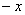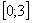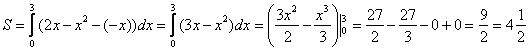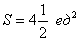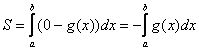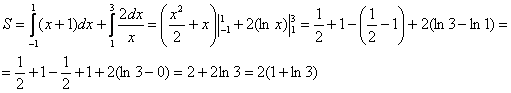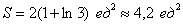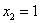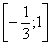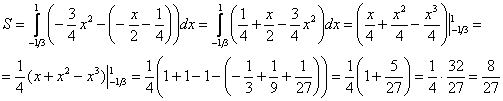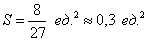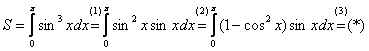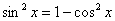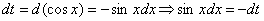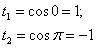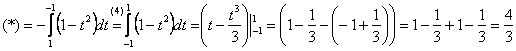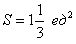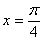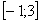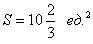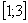Что означает площадь под графиком v t
Как по графику скорости посчитать перемещение
По графику скорости от времени v(t) можно найти перемещение тела. Для этого нужно уметь рассчитывать площади плоских фигур.
По-английски «Square» – значит «площадь». Первая буква этого слова – буква «S». Перемещение обозначают буквой S потому, что S – это площадь фигуры, заключенной между линией скорости и горизонтальной осью времени.
Как вычислить площади плоских фигур
Площадь прямоугольника
Площадь прямоугольника (рис. 1а) можно найти, перемножив две его перпендикулярные стороны:
Площадь трапеции
Примечание: Трапеция – это четырехугольник, две его стороны параллельные, а две другие – не параллельные. Параллельные стороны называются основаниями трапеции.
Умножив полусумму оснований трапеции на ее высоту, получим площадь (рис. 1б) трапеции:
Площадь прямоугольного треугольника
Для прямоугольного треугольника (рис. 1в) площадь можно вычислить, перемножив два его катета и взяв половину от получившегося произведения:
Скорость не меняется
Пусть тело движется по прямой и при этом его скорость не изменяется (остается одной и той же). На языке математики «скорость не изменяется» можно записать так:
На графике для скорости v(t) такая скорость обозначается горизонтальной линией. На рисунке 2 эта линия обозначена синим цветом.
Примечание: Движение с постоянной (т. е. с одной и той же) скоростью называют равномерным движением.
Если скорость направлена по оси движения – линия лежит выше оси t времени (рис. 2а).
А когда скорость направлена против оси движения – линия скорости располагается ниже оси t времени (рис. 2б). Математики в таком случае говорят: «Скорость имеет отрицательную проекцию на ось».
Какую бы проекцию не имела скорость – положительную, или отрицательную, длина вектора скорости остается положительной. Поэтому, когда мы вычисляем площадь фигуры, то не учитываем знак «минус» для скорости (рис. 2б).
В обоих случаях перемещение тела можно вычислить по формуле:
\[ \large S = v_ <0>\cdot (t_ <2>— t_<1>) \]
Примечание: Перемещение тела – это всегда либо нулевая, либо положительная величина S. Математики словосочетание «либо нулевая, либо положительная» заменят одним словом «не отрицательная».
Скорость увеличивается
Когда скорость тела увеличивается, то линия скорости на графике v(t) всегда располагается так, чтобы с ростом времени удаляться от оси времени. Чем больше времени пройдет, тем дальше от горизонтали располагаются точки, лежащие на линии скорости (рис. 3).
Примечание: Движение с возрастающей скоростью называют равноускоренным движением.
Когда тело движется по направлению оси, линия скорости расположена выше горизонтальной оси времени (рис 3а).
А если тело движется против оси, линия скорости располагается ниже горизонтальной оси времени (рис. 3б).
Вычислим перемещение тела, движущегося в положительном направлении оси Ox. Для тела, движущегося противоположно оси, перемещение рассчитывается аналогично.
Выбор интервала времени влияет на то, будем ли мы вычислять площадь трапеции (рис. 4а), или прямоугольного треугольника (рис. 4б).
На графике скорости v(t) для рисунка 4а перемещение с помощью трапеции вычисляется так:
\[ \large S = \frac<1> <2>\cdot (v_ <1>+ v_<2>) \cdot (t_ <2>— t_<1>) \]
А для рисунка 4б перемещение тела найдем с помощью площади треугольника:
\[ \large S = \frac<1> <2>\cdot v_ <2>\cdot (t_ <2>— 0) \]
Скорость уменьшается
Когда тело замедляется и его скорость уменьшается, с ростом времени линия скорости приближается к горизонтальной оси t
Примечание: Движение с уменьшающейся по модулю скоростью называют равнозамедленным движением.
Будем вычислять перемещение тела, движущегося в положительном направлении оси Ox. Аналогичным способом рассчитывается перемещение тела, движущегося противоположно оси.
От того, какой интервал времени нас интересует, зависит, будем ли мы вычислять площадь трапеции (рис. 6а), или треугольника (рис. 6б).
Найдем на графике v(t) перемещение с помощью площади трапеции для рисунка 6а:
\[ \large S = \frac<1> <2>\cdot (v_ <1>+ v_<2>) \cdot (t_ <2>— t_<1>) \]
А для рисунка 6б перемещение тела найдем с помощью площади треугольника:
\[ \large S = \frac<1> <2>\cdot v_ <1>\cdot (t_ <2>— t_<1>) \]
Выводы
На графике v(t) перемещение – это:
Определенный интеграл. Как вычислить площадь фигуры
Переходим к рассмотрению приложений интегрального исчисления. На этом уроке мы разберем типовую и наиболее распространенную задачу – как с помощью определенного интеграла вычислить площадь плоской фигуры. Наконец-то ищущие смысл в высшей математике – да найдут его. Мало ли. Придется вот в жизни приближать дачный участок элементарными функциями и находить его площадь с помощью определенного интеграла.
Для успешного освоения материала, необходимо:
1) Разбираться в неопределенном интеграле хотя бы на среднем уровне. Таким образом, чайникам для начала следует ознакомиться с уроком Неопределенный интеграл. Примеры решений.
2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл. Наладить теплые дружеские отношения с определенными интегралами можно на странице Определенный интеграл. Примеры решений.
В действительности, для того чтобы находить площадь фигуры не надо так уж много знаний по неопределенному и определенному интегралу. Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа, поэтому гораздо более актуальным вопросом будут ваши знания и навыки построения чертежей. В этой связи полезно освежить в памяти графики основных элементарных функций, а, как минимум, уметь строить прямую, параболу и гиперболу. Сделать это можно (многим – нужно) с помощью методического материала Графики и свойства элементарных функций и статьи о геометрических преобразованиях графиков.
Собственно, с задачей нахождения площади с помощью определенного интеграла все знакомы еще со школы, и мы мало уйдем вперед от школьной программы. Этой статьи вообще могло бы и не быть, но дело в том, что задача встречается в 99 случаев из 100, когда студент мучается от ненавистной вышки с увлечением осваивает курс высшей математики.
Материалы данного практикума изложены просто, подробно и с минимумом теории.
Начнем с криволинейной трапеции.
Криволинейной трапецией называется плоская фигура, ограниченная осью 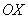
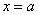
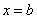
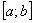
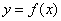
Тогда площадь криволинейной трапеции численно равна определенному интегралу 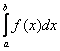
То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Например, рассмотрим определенный интеграл 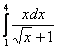
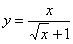
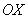
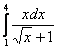
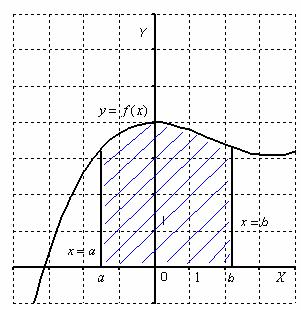
Вычислить площадь фигуры, ограниченной линиями 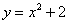
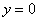
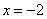
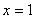
Это типовая формулировка задания. Первый и важнейший момент решения – построение чертежа. Причем, чертеж необходимо построить ПРАВИЛЬНО.
При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. Графики функций выгоднее строить поточечно, с техникой поточечного построения можно ознакомиться в справочном материале Графики и свойства элементарных функций. Там же можно найти очень полезный применительно к нашему уроку материал – как быстро построить параболу.
В данной задаче решение может выглядеть так.
Выполним чертеж (обратите внимание, что уравнение 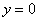
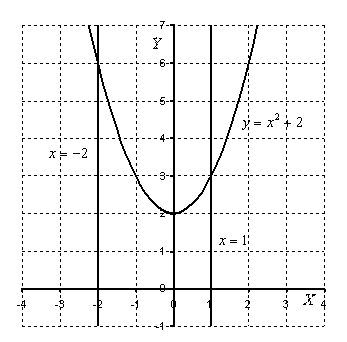
Штриховать криволинейную трапецию я не буду, здесь очевидно, о какой площади идет речь. Решение продолжается так:
На отрезке 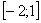
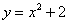
Ответ:
У кого возникли трудности с вычислением определенного интеграла и применением формулы Ньютона-Лейбница 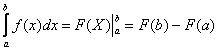
После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ. В данном случае «на глазок» подсчитываем количество клеточек в чертеже – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получился, скажем, ответ: 20 квадратных единиц, то, очевидно, что где-то допущена ошибка – в рассматриваемую фигуру 20 клеточек явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Вычислить площадь фигуры, ограниченной линиями 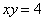
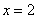
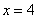
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Что делать, если криволинейная трапеция расположена под осью 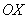
Вычислить площадь фигуры, ограниченной линиями 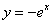
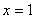
Решение: Выполним чертеж: 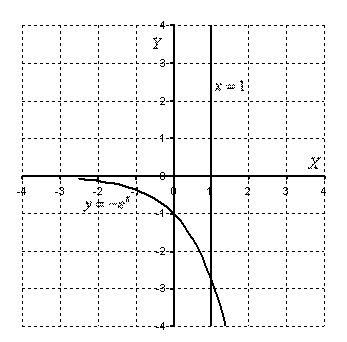
Если криволинейная трапеция расположена под осью 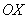
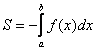
В данном случае:
Ответ:
Внимание! Не следует путать два типа задач:
1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.
2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому, от простейших школьных задачек переходим к более содержательным примерам.
Найти площадь плоской фигуры, ограниченной линиями 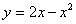
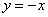
Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы 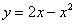
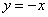
Значит, нижний предел интегрирования 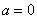
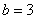
Этим способом лучше, по возможности, не пользоваться.
Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Техника поточечного построения для различных графиков подробно рассмотрена в справке Графики и свойства элементарных функций. Тем не менее, аналитический способ нахождения пределов все-таки приходится иногда применять, если, например, график достаточно большой, или поточенное построение не выявило пределов интегрирования (они могут быть дробными или иррациональными). И такой пример, мы тоже рассмотрим.
Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж: 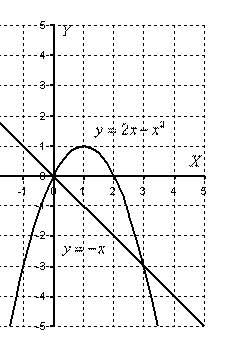
Повторюсь, что при поточечном построении пределы интегрирования чаще всего выясняются «автоматом».
А теперь рабочая формула: Если на отрезке 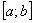
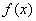
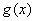
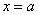
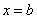
Здесь уже не надо думать, где расположена фигура – над осью или под осью, и, грубо говоря, важно, какой график ВЫШЕ (относительно другого графика), а какой – НИЖЕ.
В рассматриваемом примере очевидно, что на отрезке 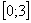
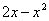
Завершение решения может выглядеть так:
Искомая фигура ограничена параболой 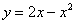
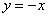
На отрезке 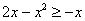
Ответ:
На самом деле школьная формула для площади криволинейной трапеции в нижней полуплоскости (см. простенький пример №3) – частный случай формулы 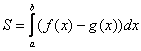
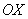
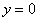
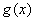
А сейчас пара примеров для самостоятельного решения
Найти площадь фигуры, ограниченной линиями 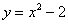
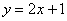
Найти площадь фигуры, ограниченной линиями 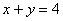
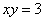
В ходе решения задач на вычисление площади с помощью определенного интеграла иногда случается забавный казус. Чертеж выполнен правильно, расчеты – правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз лажался ваш покорный слуга. Вот реальный случай из жизни:
Вычислить площадь фигуры, ограниченной линиями 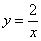
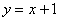
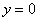
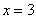
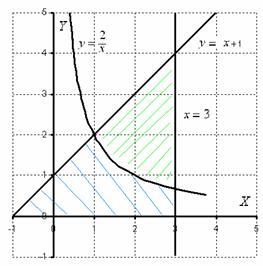
Решение: Сначала выполним чертеж:
…Эх, чертеж хреновенький вышел, но вроде всё разборчиво.
Фигура, площадь которой нам нужно найти, заштрихована синим цветом (внимательно смотрите на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована зеленым цветом!
Этот пример еще полезен и тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:
1) На отрезке 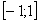
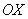
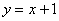
2) На отрезке 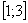
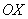
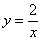
Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:
Ответ:
Переходим еще к одному содержательному заданию.
Вычислить площадь фигуры, ограниченной линиями 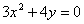
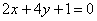
Представим уравнения в «школьном» виде 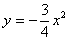
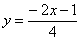

Из чертежа видно, что верхний предел у нас «хороший»: 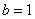
Но чему равен нижний предел?! Понятно, что это не целое число, но какое? Может быть 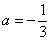
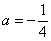
В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.
Найдем точки пересечения прямой 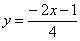
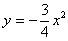
Для этого решаем уравнение: 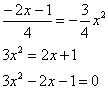
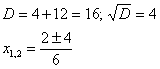
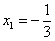
Действительно, 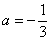
Дальнейшее решение тривиально, главное, не запутаться в подстановках и знаках, вычисления здесь не самые простые.
На отрезке 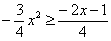
Ответ:
Ну, и в заключение урока, рассмотрим два задания сложнее.
Вычислить площадь фигуры, ограниченной линиями 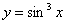
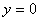
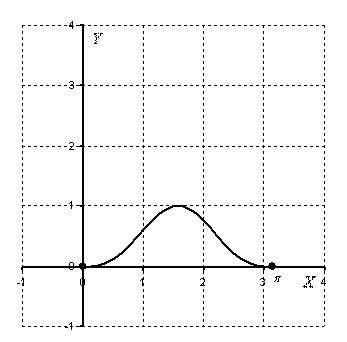
Решение: Изобразим данную фигуру на чертеже.
Блин, забыл график подписать, а переделывать картинку, простите, не хотца. Не чертёжный, короче, сегодня день =)
Для поточечного построения необходимо знать внешний вид синусоиды (и вообще полезно знать графики всех элементарных функций), а также некоторые значения синуса, их можно найти в тригонометрической таблице. В ряде случаев (как в этом) допускается построение схематического чертежа, на котором принципиально правильно должны быть отображены графики и пределы интегрирования.
С пределами интегрирования здесь проблем нет, они следуют прямо из условия: 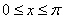
На отрезке 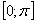
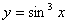
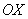
(1) Как интегрируются синусы и косинусы в нечетных степенях можно посмотреть на уроке Интегралы от тригонометрических функций. Это типовой прием, отщипываем один синус.
(2) Используем основное тригонометрическое тождество в виде
(3) Проведем замену переменной 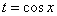
Новые пределы интегрирования:
У кого совсем плохи дела с заменами, прошу пройти на урок Метод замены в неопределенном интеграле. Кому не очень понятен алгоритм замены в определенном интеграле, посетите страницу Определенный интеграл. Примеры решений.
(4) Здесь мы использовали свойство определенного интеграла 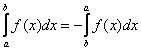
Ответ:
Вычислить площадь фигуры, ограниченной линиями 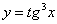
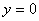
Это пример для самостоятельного решения. Полное решение и ответ на нижнем этаже.
Вот, пожалуй, и все основные принципиальные приёмы нахождения площадей. Помимо рассмотренных методов интегрирования, иногда приходится применять формулу интегрирования по частям в определенном интеграле, что не представляет собой особых трудностей. Какой-то интересный пример придумать сложно, … хотя… арккотангенса вроде еще нигде не встречалось:
Вычислить площадь фигуры, ограниченной линиями 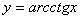
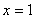
Полного решения не будет, надо же вас немного помучить. А правильный ответ скажу: 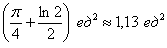
Пример 2: Решение:
Выполним чертеж: 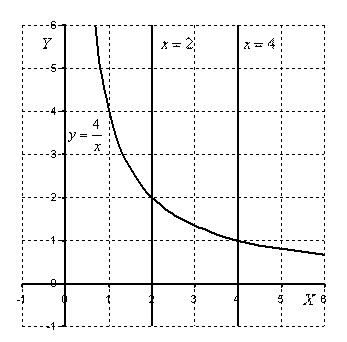
На отрезке 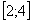
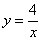
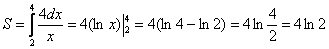
Ответ: 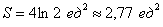
Примечание: В задачах на нахождение площадей преподаватели часто требуют записывать ответ не только точно, но и, в том числе, приближенно.
Пример 5: Решение:
Выполним чертеж: 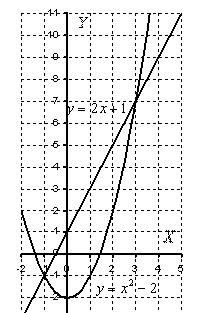
На отрезке 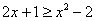

Ответ:
Пример 6: Решение:
Выполним чертеж. 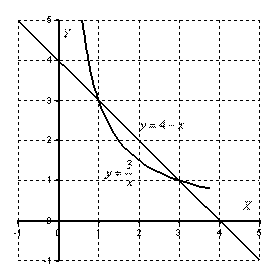
На отрезке 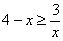
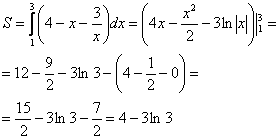
Ответ:
Пример 10: Решение:
Изобразим данную фигуру на чертеже: 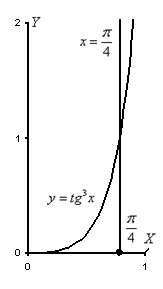
На отрезке 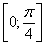
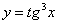
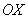

Ответ: 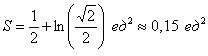
Примечание: обратите внимание, как берется интеграл от тангенса в кубе, здесь использовано следствие основного тригонометрического тождества 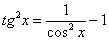
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5