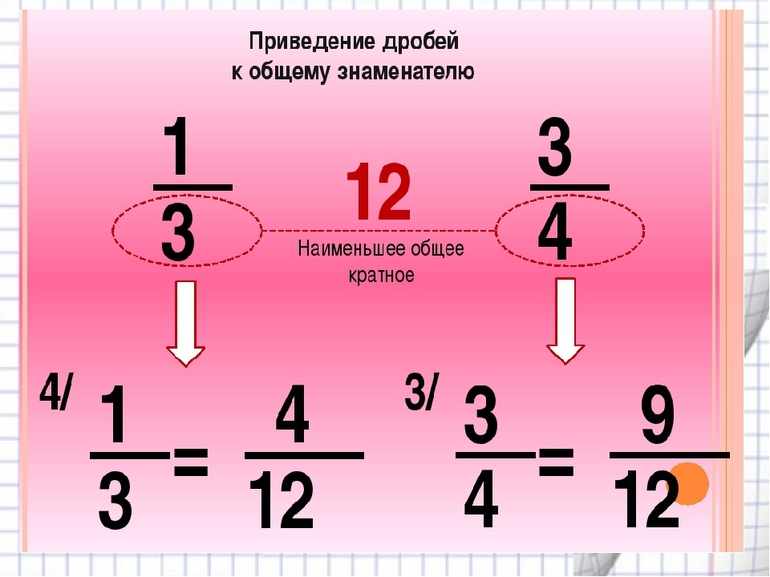
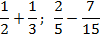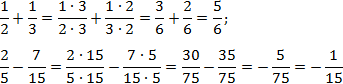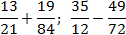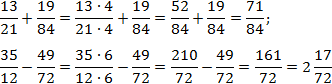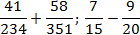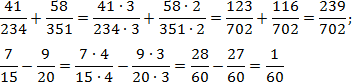Что означает привести дробь к общему знаменателю
Приведение дробей к общему знаменателю.
Общий знаменатель и дополнительный множитель.
У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:
Пример разных знаменателей у дробей:
Как привести к общему знаменателю дроби?
У первой дроби знаменатель равен 3, у второй равен 13. Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.
Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.
Вторую дробь умножаем на дополнительный множитель 3.
Мы привели к общему знаменателю дроби:
Наименьший общий знаменатель.
Рассмотрим еще пример:
Приведем дроби \(\frac<5><8>\) и \(\frac<7><12>\) к общему знаменателю.
Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.
Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.
Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.
Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.
Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ сократить.
Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.
Например:
Приведите дроби \(\frac<1><4>\) и \(\frac<9><16>\) к наименьшему общему знаменателю.
Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:
Вопросы по теме:
Любые ли две дроби можно привести к одному общему знаменателю?
Ответ: да.
К какому знаменателю принято приводить дроби?
Ответ: к наименьшему общему знаменателю.
Пример №1:
Для дроби \(\frac<1><2>\) запишите равную дробь со знаменателем: а) 12 б) 18 в) 50?
Решение:
а) Число 2 нужно умножить на 6, чтобы получить 12. Следовательно, мы всю дробь умножаем на дополнительный множитель 6.
б) Число 2 нужно умножить на 9, чтобы получить 18. Следовательно, мы всю дробь умножаем на дополнительный множитель 9.
в) Число 2 нужно умножить на 25, чтобы получить 50. Следовательно мы всю дробь умножаем на дополнительный множитель 25.
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
Задача. Найдите значения выражений:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Приведение дроби к наименьшему общему знаменателю: правило, примеры решений
В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Приведение дробей к общему знаменателю
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Пример 1. Общий знаменатель
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменатель
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
По правилу, сначала найдем НОК знаменателей дробей.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
Далее вычислим дополнительные множители для каждой дроби.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
3 2 · 36 = 108 72 5 6 · 12 = 60 72 3 8 · 9 = 27 72 17 18 · 4 = 68 72
Алгоритм приведения дробей к общему знаменателю в 5 классе
Операция приведения дробей к общему знаменателю в 5 классе используется при выполнении сложения и вычитания, а также для упрощения выражений. Делать это позволяет определенная методика, которой следует придерживаться. Она также оптимизирует вычислительный процесс, экономя драгоценное время и уменьшая число ошибок на начальной стадии обучения. Перед ее изучением математики рекомендуют получить базовые знания.
Базовая информация
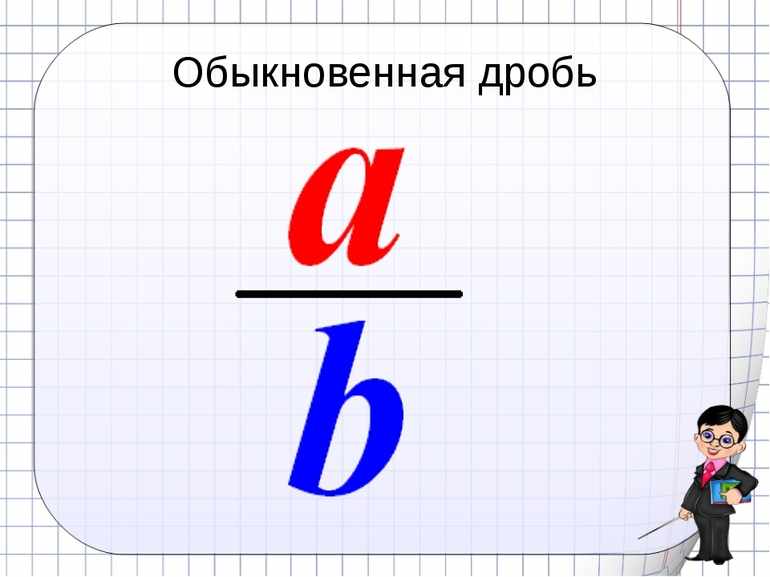
Обыкновенная дробь — значение, состоящее из верхней части (числителя) и нижней (знаменателя). Они разделены чертой. Обыкновенные дробные величины бывают трех типов: правильными, неправильными и смешанными. К первой группе относятся значения, числитель которых меньше знаменателя, ко второй — наоборот. Промежуточным значением является смешанное число. Оно состоит из целой и дробной частей.
Чтобы выполнить арифметические операции сложения и вычитания, нужно привести дроби к общему знаменателю (ОЗ). Последнее математическое действие обусловлено нахождением наименьшего общего кратного (НОК). Для этой операции могут потребоваться:
Изучение приведения дробей к ОЗ всегда начинается с признаков делимости.
Признаки делимости
Перед ознакомлением с признаками деления чисел нужно внести определенные термины, чтобы учащиеся не путались в правилах. Цифры — математические символы, которые используются для создания чисел. Числа — количественные характеристики, необходимые для выражения фактических данных. У каждого значения существует разрядная сетка (РС). Она состоит из разрядов, именуемых единицами, десятками, сотнями, тысячами и т. д.
Работа со смешанными числами
Для преобразования неправильной дроби в смешанное число используется определенный алгоритм. Он имеет такой вид:
Специалисты рекомендуют после алгоритма разобрать его реализацию на примере дробного выражения 25/3. Правильная методика преобразования выглядит следующим образом:
Однако нужно уметь выполнять обратную операцию (проверочную) преобразования смешанного числа в неправильную дробь. Для этого требуется выполнить пункты алгоритма в обратном порядке:
Иными словами, следует умножить знаменатель на целую часть, а затем к результату прибавить числитель.
Приведение к одному знаменателю
Приведение к общему знаменателю — довольно простая операция. Для этого необходимо разобрать все случаи, а также алгоритмы, используемые для этого:
Общие сомножители
Иногда следует применить все знания, чтобы привести дроби к знаменателю в 8 классе (дисциплина — «алгебра и начало анализа»), который должен быть общим. Выход из ситуации — нахождение НОК. Операция осуществляется по алгоритму:
Специалисты рекомендуют разбирать реализацию алгоритма на примере. Для этого следует привести 2 дроби 3/8 и 5/12 к общему знаменателю:
Для проверки результатов можно воспользоваться специальными онлайн-сервисами. Однако их математики рекомендуют применять только для сопоставления с ответами, полученными при решении ручным методом без использования средств вычислительной техники.
Таким образом, для приведения дробей к ОЗ необходимо знать признаки делимости, а также основные методики выполнения этой операции.
Приведение дробей к общему знаменателю
Общий знаменатель обыкновенных дробей
Любые дроби с разными знаменателями в математике можно привести к одному и тому же общему знаменателю — заменить на равные им дроби с одинаковым знаменателем.
Есть два вида знаменателей:
Общий знаменатель — это число или выражение, которое является знаменателем для двух и более обыкновенных дробей.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Наименьший общий знаменатель — наименьшее общее кратное знаменателей данных дробей.
Производить данную операцию необходимо в ряде случаев.
Как привести дроби к общему знаменателю, алгоритм
Чтобы осуществить операцию приведения, необходимо применить основное свойство дробей: если числитель и знаменатель дроби умножить на одно и то же число, отличное от нуля, дробь не изменится. То есть если подобрать правильные множители, то можно привести знаменатели к одному и тому же числу. Искомые множители называют дополнительными.
Это объяснение лежит в основе общего правила приведения дробей.
Существует несколько способов привести дроби к общему или наименьшему общему знаменателю.
Умножение «крест-накрест»
Самый простой способ — умножение «крест-накрест». Применяется следующий пошаговый алгоритм:
Недостаток этого метода — в размерах вычислений. При умножении могут получиться большие числа, которыми тяжело оперировать.
Метод общих делителей
Иногда один из знаменателей дроби уже делится на другой без остатка. В таком случае нет нужды перемножать их, количество действий сокращается.
Этот метод хорош тем, что является более кратким вариантом умножения «крест-накрест». При этом его невозможно использовать при решении примеров, в которых числа в знаменателях не делятся друг на друга.
Метод наименьшего общего кратного
Суть приведения заключается в том, чтобы найти такое число, которое делится на каждый из знаменателей. К этому числу и необходимо привести знаменатели обеих дробей.
Наименьшее общее кратное (НОК) — это наименьшее число, на которое делится каждый из знаменателей. Обозначается он как НОК (a; b).
НОК (3; 4) = 12; НОК (8; 12) = 24.
Иногда найти НОК можно «на глаз», не выполняя дополнительных расчетов. К примеру, НОК (6; 9) = 18. Однако иногда на это может понадобиться больше времени. Описание примера таких вычислений приведено в примерах решения задач ниже.
Таким образом, основное преимущество это метода заключается в краткости вычислений. При этом его недостатком является сложность нахождения НОК в некоторых случаях.
Примеры задач с подробным решением
Задача
Решение
Для начала применим метод «крест-накрест». Тогда:
Получившуюся дробь можно сократить на 5:
Однако решение можно сократить, применив метод общих делителей. 15 делится на 5 без остатка. При таком делении дополнительным множителем для первой дроби будет число 3:
Задача
Решение
Решить эту задачу методом общих делителей невозможно, ведь 20 не делится без остатка на 15. При этом оба числа являются большими:
Вычисление методом «крест-накрест» будет слишком большим.
Оптимальным вариантом решения является метод наименьшего общего кратного.
\(НОК (15; 20) = 5\cdot3\cdot4=60\)
При делении 60 на знаменатели обеих дробей получаются дополнительные множители 4 и 3. Используем их для вычислений: