Что означает произвольная точка плоскости
произвольная точка
Смотреть что такое «произвольная точка» в других словарях:
Изолированная точка множества — Изолированная точка в общей топологии это такая точка множества, что пересечение некоторой её окрестности с множеством состоит только из этой точки. Содержание 1 Определение 2 Связанные определения … Википедия
Изолированная точка — в общей топологии это такая точка множества, что пересечение некоторой её окрестности с множеством состоит из единственной точки. Содержание 1 Определение 2 Связанные определения 3 Свойства … Википедия
КОНИЧЕСКИЕ СЕЧЕНИЯ — плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину (рис. 1). С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек,… … Энциклопедия Кольера
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и … Энциклопедия Кольера
Линия — I Линия (от лат. linea) геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной… … Большая советская энциклопедия
Линия (геометрич. понятие) — Линия (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной геометрии рассматриваются… … Большая советская энциклопедия
ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО — совокупность двух объектов: множества X, состоящего из элементов произвольной природы, наз. точками данного пространства, и из введенной в это множество топологической структуры, или топологии, все равно открытой или замкнутой (одна переходит в… … Математическая энциклопедия
АБЕЛЕВ ДИФФЕРЕНЦИАЛ — голоморфный или мероморфный дифференциал на компактной, или замкнутой, римановой поверхности S(см. Дифференциал на римановой поверхности). Пусть g род поверхности S; а1b1 а 2b2. agbg циклы канонич. базиса гомологии S. В зависимости от характера… … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия
Кривая Пеано — общее название для параметрических кривых, образ которых содержит квадрат (или, в более общем смысле, открытые области пространства) Содержание 1 Свойства 2 Примеры 3 Обобщения … Википедия
Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
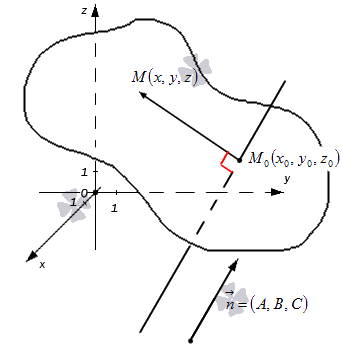
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Раскроем чуть шире смысл теорем.
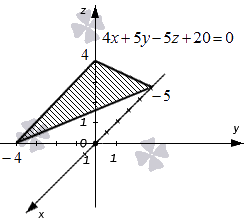
Укажем пример как иллюстрацию этих утверждений.
Общее уравнение плоскости, проходящей через точку
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Решение
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Возможно получить это уравнение другим способом.
Решение
Рассмотрим два способа решения.
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
Неполное общее уравнение плоскости
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
Решение
Задачу возможно решить еще одним способом.
Решение
Пункт 2. Вывод уравнения плоскости по точке и двум направляющим.
Пусть даны точка 

Обозначим координаты направляющих, например, так: 

Первый способ. Можно найти нормаль к плоскости как векторное произведение 2 направляющих векторов 
Однако можно также получить уравнение плоскости сразу, без вычисления векторного произведения:
Второй способ.Возьмём произвольную точку 



 | Тогда смешанное произведение 0, то есть определитель, составленный из них, равен 0:  |
Вычисляя этот определитель, мы получим в качестве результата некоторое уравнение, содержащее x,y,z. А если начальная точка (0,0,0), то уравнение будет вычисляться с помощью такого определителя: 
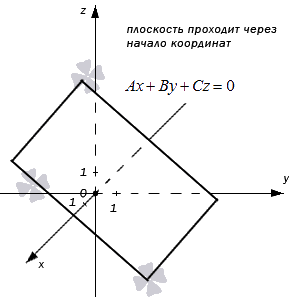
Пример.Построить уравнение плоскости, проходящей через начало координат, параллельно 2 направляющим (1,2,3) и (1,1,1).
Решение. 


Для удобства, чтобы 1-й коэффициент был положителен, можно домножить на 

Замечание.Векторы 

Замечание. Построение уравнения плоскости по трём точкам. Если дано 3 точки, достаточно взять 2 направляющих 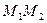


Лекция № 7. 14. 10. 2016
Пункт 3. Расстояние от точки до плоскости.
Пусть дано уравнение плоскости 

 | Возможно, она лежит в плоскости (тогда расстояние по формуле автоматически получится 0). Но в общем случае она не принадлежит плоскости. Мы не знаем, где основание перпендикуляра, более того, его и не потребуется искать. |
Возьмём произвольную точку 



Если подставить в уравнение плоскости (в числителе) точку, лежащую в плоскости, то получим 0. В общем же случае, результат подстановки некоторой точки, не лежащей в плоскости, в уравнение плоскости, характеризует удаление от плоскости.
Пункт 4. Взаимное расположение плоскостей
Пусть даны 2 плоскости.
Если рассматривать это как систему уравнений, то видим, что 2 уравнения и 3 переменных, то есть по меньшей мере одна свободная переменная. Это означает, что если решения есть, то их бесконечно много. Это и есть все точки, принадлежащие прямой, являющейся пересечением плоскостей.
Если 
Если 
Если пропорциональность нарушена среди каких-то из первых 3 дробей, то плоскости пересекаются по прямой.
Пункт 5. Угол между плоскостями и метод его нахождения.
Прямая в пространстве.
Для прямой на плоскости и для плоскости в пространстве есть однозначно определённое направление нормали (перпендикуляра) т.к. там размерности рассматриваемых многообразий 1 и 2 (2 и 3 соответственно), то есть «не хватает» одной размерности. А для прямой в пространстве не хватает 2 размерностей (1 и 3). Это совершенно новый случай, здесь нельзя однозначно задать перпендикуляр. Есть целая плоскость, перпендикулярная прямой, то есть бесконечное число нормалей. А вот направляющий вектор однозначно определён (с точность до его длины, конечно). Это проявится в том, что мы получим другой тип уравнений.
Точка в системе плоскостей проекций h v и w
Точка в системе плоскостей проекций 
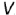

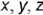
Для получения изображений предметов на чертежах французский геометр Гаспар Монж (основоположник начертательной геометрии как науки и автор первой, изданной в Париже, книги по начертательной геометрии «Geometrie descriptive», 1795 г.) предложил следующий метод — метод параллельного прямоугольного проецирования на взаимно перпендикулярные плоскости проекций.
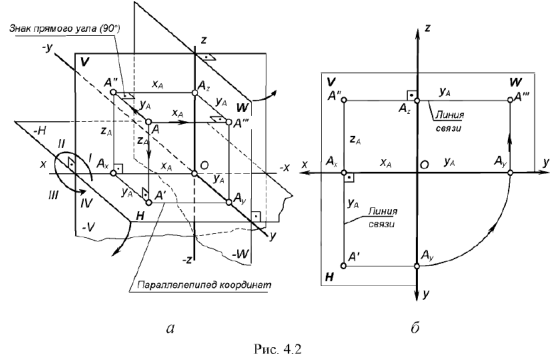
На рис 4.2, а показано наглядное изображение трех взаимно перпендикулярных плоскостей проекций:
Плоскости проекций, пересекаясь в пространстве, делят пространство на восемь частей, которые называют октантами Слева от плоскости проекций 
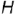
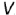

В качестве предмета проецирования на рис. 4.2, а взята точка 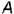
Плоскости проекций пересекаются между собой по линиям, которые называют осями проекций: ось 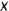
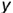
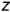
Оси проекций принимают за оси координат, определяющих положение точки в пространстве, и называют системой прямоугольных координат 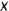
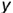
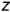
Оси проекций пересекаются в точке 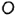
Расстояния точки 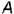
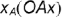

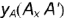
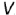
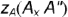
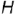
Чтобы перейти от наглядного изображения системы трех плоскостей проекций 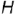
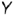

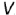
На чертеже (см. рис. 4.2, 6) координатные оси проекций располагают следующим образом:
Чертеж предмета содержит изображения проекций этого предмета.
Проекции предмета строятся как проекции совокупного множества точек, определяющих и задающих поверхность этого предмета. Точки объединяются в более общие известные из геометрии элементы: прямые, плоскости и различные поверхности (гранные, цилиндрические, конические и т.д.).
Чертеж точки содержит ее проекции, которые строятся по координатам этой точки.
На рис. 4.2, б показано построение чертежа произвольной точки 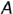
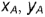
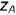
. Запомните! Горизонтальная 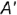
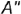
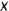
Чтобы построить профильную 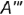
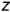
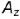
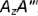
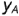
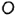
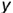
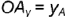
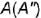
. Запомните! Фронтальная 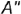
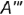
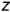
На рис. 4.3 показано построение чертежа точки 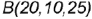
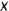
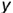
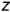
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
произвольная точка
Смотреть что такое «произвольная точка» в других словарях:
Изолированная точка множества — Изолированная точка в общей топологии это такая точка множества, что пересечение некоторой её окрестности с множеством состоит только из этой точки. Содержание 1 Определение 2 Связанные определения … Википедия
Изолированная точка — в общей топологии это такая точка множества, что пересечение некоторой её окрестности с множеством состоит из единственной точки. Содержание 1 Определение 2 Связанные определения 3 Свойства … Википедия
КОНИЧЕСКИЕ СЕЧЕНИЯ — плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину (рис. 1). С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек,… … Энциклопедия Кольера
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и … Энциклопедия Кольера
Линия — I Линия (от лат. linea) геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной… … Большая советская энциклопедия
Линия (геометрич. понятие) — Линия (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной геометрии рассматриваются… … Большая советская энциклопедия
ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО — совокупность двух объектов: множества X, состоящего из элементов произвольной природы, наз. точками данного пространства, и из введенной в это множество топологической структуры, или топологии, все равно открытой или замкнутой (одна переходит в… … Математическая энциклопедия
АБЕЛЕВ ДИФФЕРЕНЦИАЛ — голоморфный или мероморфный дифференциал на компактной, или замкнутой, римановой поверхности S(см. Дифференциал на римановой поверхности). Пусть g род поверхности S; а1b1 а 2b2. agbg циклы канонич. базиса гомологии S. В зависимости от характера… … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия
Кривая Пеано — общее название для параметрических кривых, образ которых содержит квадрат (или, в более общем смысле, открытые области пространства) Содержание 1 Свойства 2 Примеры 3 Обобщения … Википедия