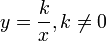Что означает прямо пропорционально
Прямая пропорциональность
Содержание
Пример
Масса керосина пропорциональна его объёму: 2 л керосина весят 1,6 кг, 5 л весят 4 кг, 7 л весят 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.
Коэффициент пропорциональности
Прямая пропорциональность
Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.
Математически прямая пропорциональность записывается в виде формулы:
Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).
Математически обратная пропорциональность записывается в виде формулы:
См. также
Источники
Полезное
Смотреть что такое «Прямая пропорциональность» в других словарях:
прямая пропорциональность — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN direct ratio … Справочник технического переводчика
прямая пропорциональность — tiesioginis proporcingumas statusas T sritis fizika atitikmenys: angl. direct proportionality vok. direkte Proportionalität, f rus. прямая пропорциональность, f pranc. proportionnalité directe, f … Fizikos terminų žodynas
ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова
Пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова
пропорциональность — и; ж. 1. к Пропорциональный (1 зн.); соразмерность. П. частей. П. телосложения. П. представительства в парламенте. 2. Матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент пропорциональности. Прямая п. (при которой с… … Энциклопедический словарь
пропорциональность — и; ж. 1) к пропорциональный 1); соразмерность. Пропорциона/льность частей. Пропорциона/льность телосложения. Пропорциона/льность представительства в парламенте. 2) матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент… … Словарь многих выражений
Обратная пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
линейная зависимость — прямая пропорциональность. множитель. см. константа … Идеографический словарь русского языка
Урок 23 Бесплатно Прямая и обратная пропорциональные зависимости
На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.
Прямая и обратная пропорциональность
Давайте сначала разберемся, что такое пропорциональность.
Зависимость величин друг от друга может быть прямой и обратной.
Отношение между величинами описываются прямой или обратной пропорциональностью.
Прямая пропорциональность выражается так: \(\mathbf
Обратная пропорциональность выражается так: \(\mathbf
x и y величины, зависящие друг от друга.
Пример
Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.
По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.
Какова эта зависимость, сейчас и рассмотрим.
Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.
Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.
Пусть одна клетка равна 1 см. Рассмотрим рисунок:
Ширина прямоугольника b постоянная величина
b = 4 см
a1 = 6 см
a2 = 7 см
Найдем площади прямоугольников S1 и S2
\(\mathbf
\(\mathbf
Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.
Рассмотрим другой вариант зависимости
Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см
Площадь прямоугольника S постоянная величина
S = 24 см 2
b1 = 4 см
Увеличим высоту прямоугольника- сторону прямоугольника b1 на 2 см, получим
b2 = 6 см
Найдем ширину прямоугольника- сторону a2
Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.
Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:
1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.
2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.
Примеров прямой и обратной пропорциональности множество.
Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.
Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.
Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается
Пройти тест и получить оценку можно после входа или регистрации
Алгоритм решение задач с прямой и обратной пропорциональной зависимостью
Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:
— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин
— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.
5. Записать пропорцию, учитывая характер пропорциональности величин
6. Составить уравнение
7. Найти неизвестный член уравнения (искомую величину)
8. Записать ответ задачи
Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.
Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.
Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.
Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
Пройти тест и получить оценку можно после входа или регистрации
Прямая и обратная пропорциональность
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
a и d называются крайними членами, b и c — средними.
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
Прямая и обратная пропорциональность
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
Пропорциональность
Содержание
Пример
Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.
Коэффициент пропорциональности
Символ
Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.
В юникоде для отображения используется символ U+221D.
Прямая пропорциональность
Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.
Математически прямая пропорциональность записывается в виде формулы:
Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).
См. также
Источники
Полезное
Смотреть что такое «Пропорциональность» в других словарях:
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова
ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка
Пропорциональность — 1) соразмерность элементов и их связей в одной системе; 2) принцип организации политических систем и процессов, динамическая сбалансированность политической системы. В политологическом ракурсе «пропорциональность» подразумевает выяснение целого… … Политология. Словарь.
пропорциональность — соразмерность, соизмеримость; соответствие, стройность, гармоничность, рациональность, нормальность. Ant. непропорциональность, асимметрия Словарь русских синонимов. пропорциональность соразмерность Словарь синонимов русского языка. Практический… … Словарь синонимов
ПРОПОРЦИОНАЛЬНОСТЬ — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Современная энциклопедия
ПРОПОРЦИОНАЛЬНОСТЬ — простейший вид функциональной зависимости (см. Функция). Различают прямую пропорциональность. (y =kx) и обратную пропорциональность (y=k/x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S =vt… … Большой Энциклопедический словарь
Пропорциональность — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Иллюстрированный энциклопедический словарь
пропорциональность — ПРОПОРЦИОНАЛЬНОСТЬ, соразмерность ПРОПОРЦИОНАЛЬНЫЙ, соразмерный ПРОПОРЦИОНАЛЬНО, соразмерно, соответственно … Словарь-тезаурус синонимов русской речи
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова
ПРОПОРЦИОНАЛЬНОСТЬ — англ. proportionality; нем. Proportionalitat. Простейший вид функциональной зависимости, фиксирующей соотношение между двумя величинами; показатель отношения исследуемой функции ко всему числу изучаемых случайностей. Antinazi. Энциклопедия… … Энциклопедия социологии
ПРОПОРЦИОНАЛЬНОСТЬ — (лат. proportionalis) соблюдение пропорций, рациональных структурных соотношений в экономике, согласованное развитие отраслей, сфер, регионов. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М … Экономический словарь