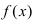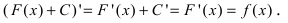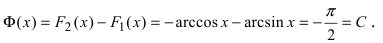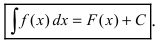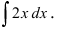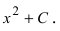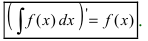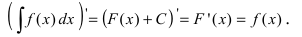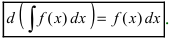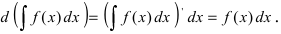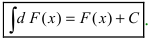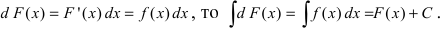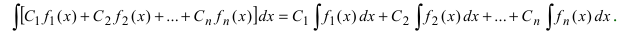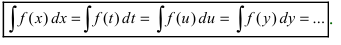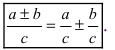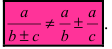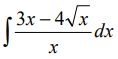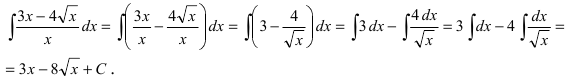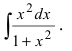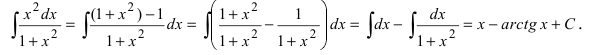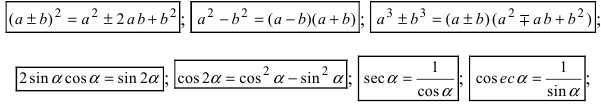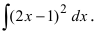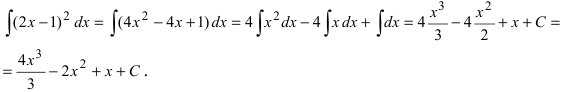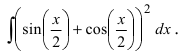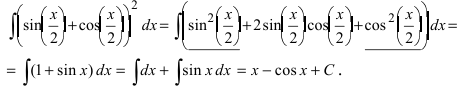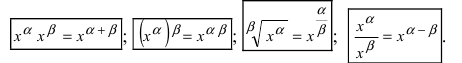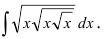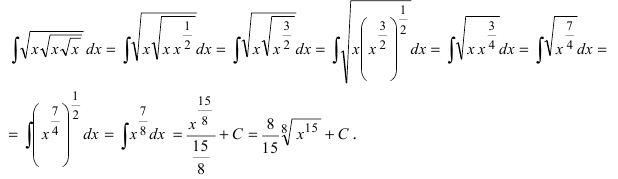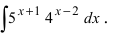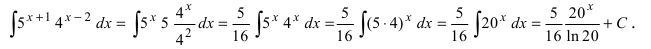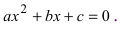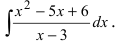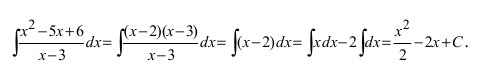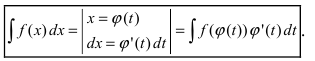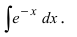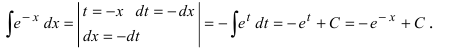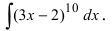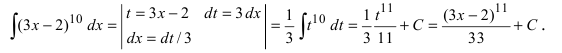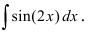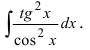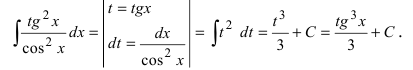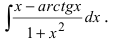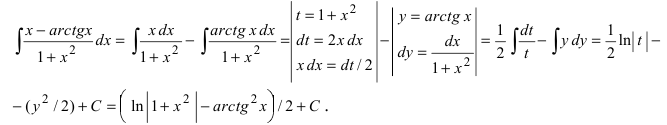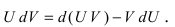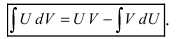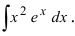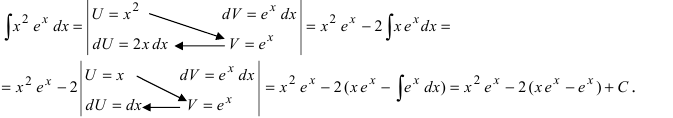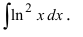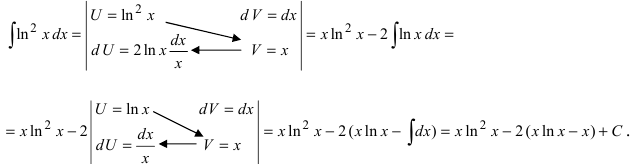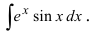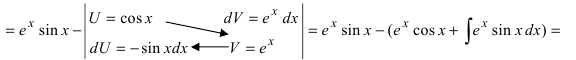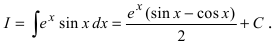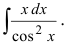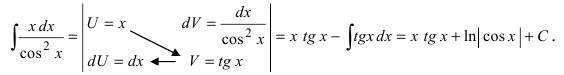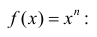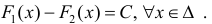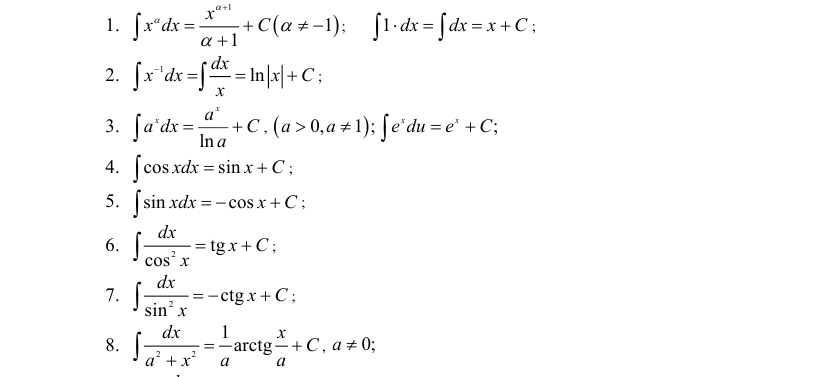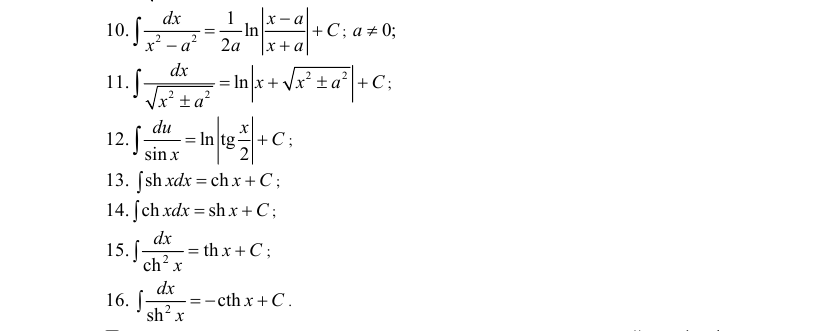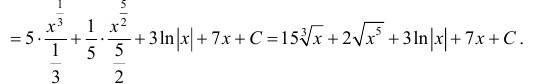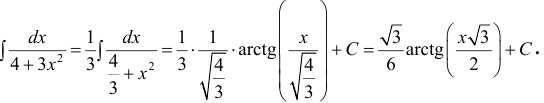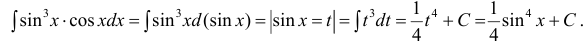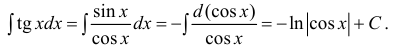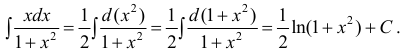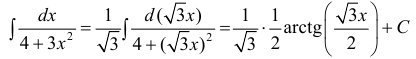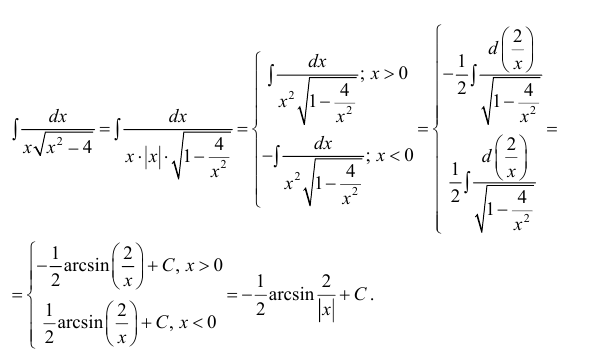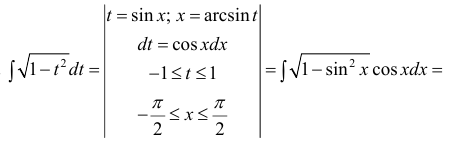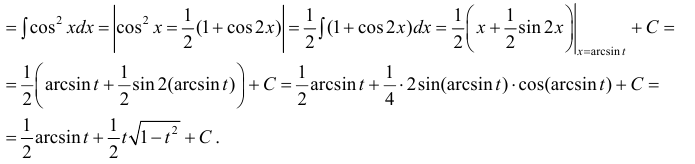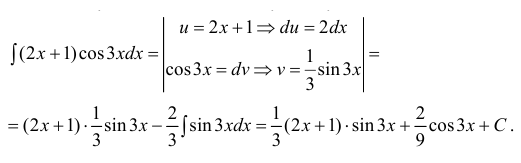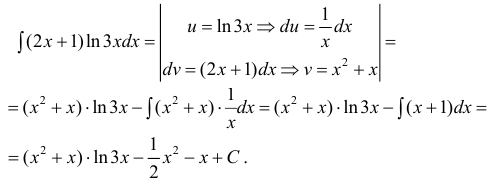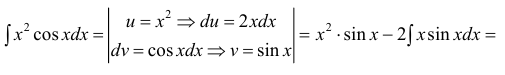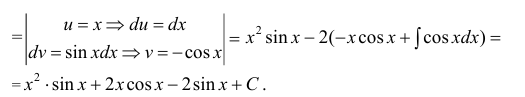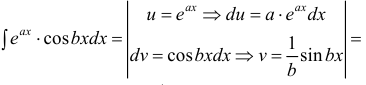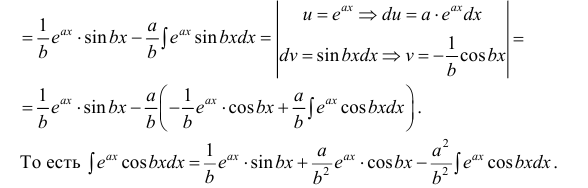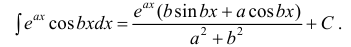Что означает возвращение к исходному интегралу

Что означает возвращение к исходному интегралу

Теорема 4.1. Если – две первообразные для функции f ( x ) на отрезке [ a ; b ], то разность между ними равна постоянному числу

Доказательство. По условию теоремы и по определению первообразной имеем: Обозначим Продифференцируем последнее равенство: С другой стороны

На основании доказанной теоремы можно записать:

Основные свойства неопределенного интеграла

1. Операции интегрирования и дифференцирования взаимообратны:

2. Если подынтегральную функцию умножить на постоянную величину, то на эту же постоянную умножается неопределенный интеграл:

3. Интеграл суммы (разности) двух функций равен сумме (разности) их интегралов:

Свойство 3 может быть применено для любого конечного числа слагаемых.

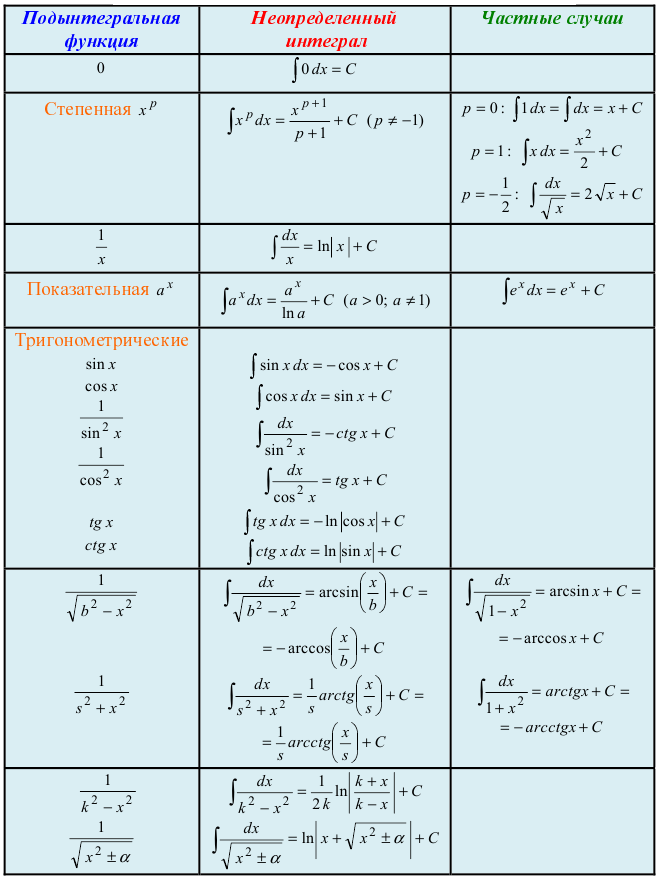
1. Табличное (непосредственное) интегрирование

Интегрирование сводится к непосредственному применению табличной формулы или нескольких из них с помощью определенных математических операций (сложения, вычитания, возведения в степень, почленного деления числителя на знаменатель и т.д.) либо формул (сокращенного умножения, тригонометрии и т.д.).

Учитывая формулу (4.2) из свойства 1, приведем таблицу основных интегралов с проверками полученных результатов.

Пример 4.1. Найти неопределенный интеграл

Здесь использованы формулы интегрирования (4.6) и (4.12)

Пример 4.2. Найти неопределенный интеграл

2. Замена переменной (метод подстановки)

Теорема 4.2. Пусть функция x =φ ( t ) определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f ( x ). Тогда, если на множестве Х функция f ( x ) имеет первообразную, то на множестве Т выполняется формула:

Доказательство. Найдем производную по x от левой и правой частей уравнения (4.21), и убедимся, что эти производные равны. Правую часть при этом будем дифференцировать по x как сложную функцию с промежуточным аргументом φ( t ). Заметим также, что

Производная левой части: по свойству обратности. Производная правой части:

Пример 4.3. Найти неопределенный интеграл

Здесь использована формула интегрирования (4.7)

Пример 4.4. Найти неопределенный интеграл

Здесь использована формула интегрирования (4.17)

3. Интегрирование по частям

– формула интегрирования по частям.

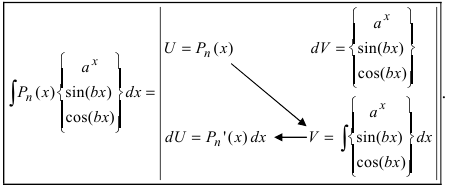
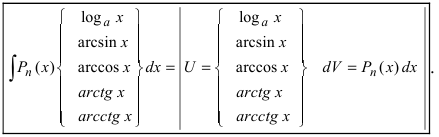
Можно указать следующие основные типы интегралов, для нахождения которых применяется интегрирование по частям:

1. где P ( x ) – многочлен, m – число. Удобно положить u = P ( x ), а в качестве dν взять остальные сомножители.

Умение разбивать подынтегральную функцию на множители u и dν оптимальным образом приходит с опытом при решении задач. Рассмотрим некоторые из них.

Пример 4.5. Найти неопределенный интеграл

Здесь использованы формулы интегрирования (4.11), (4.12), (4.22)

Пример 4.6. Найти неопределенный интеграл

Здесь использованы формулы интегрирования (4.7), (4.22)

Пример 4.7. Найти неопределенный интеграл

Перенесем интеграл J в левую часть равенства и возьмем интеграл правой части, получим

Здесь использованы формулы дифференцирования (3.17), (3.31) и интегрирования (4.20), (4.22)

Пример 4.8. Найти неопределенный интеграл

Проинтегрируем по частям полученный интеграл J, используя (4.22) :

Подставим J в исходный интеграл:

Здесь использованы формулы дифференцирования (3.23) и интегрирования (4.10), (4.22)

Источник

Методы интегрирования неопределенного интеграла с примерами решения

Содержание:

При решении многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий движения и других, вводится понятие интегрирования.

Определения

Определение: Первообразной функции

Теорема: (о существовании первообразной) Если функция f(x) непрерывна на сегменте 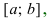то на этом интервале существует первообразная этой функции.

Доказательство:

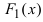
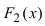
ТЗ. Если и первообразные функции f(х), то они отличаются друг от друга на постоянную величину.

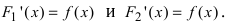
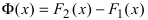
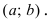
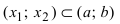
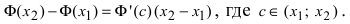
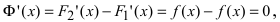
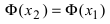
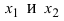
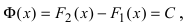
Доказательство: Пусть Введем в рассмотрение вспомогательную функцию и рассмотрим эту функцию на открытом интервале По теореме Лагранжа для любого интервала выполняется равенство По условию теоремы следовательно, . В силу произвольности точек полученное равенство выполняется для всего исследуемого интервала. Это означает, что откуда и вытекает утверждение теоремы.

Пример:

Пусть дана функция 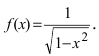Найти первообразную этой функции.

Решение:

В случае наличия двух первообразных показать, что они отличаются на постоянную величину.

Для функции существуют две первообразные 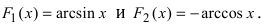Их разность

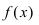
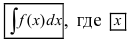
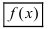
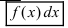
Определение: Совокупность всех первообразных функции называется неопределенным интегралом и обозначается — переменная интегрирования, — подынтегральная функция, — подынтегральное выражение.

На основании теорем можно записать, что

Определение: Отыскание всех первообразных называется неопределенным интегрированием.

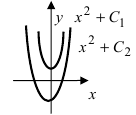
Выясним геометрический смысл неопределенного интеграла. Пусть дана функция 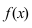и требуется найти такую кривую y = F(x), для которой в каждой ее точке тангенс угла наклона касательной равен значению функции f(х) в этой точке. Такой линией будет кривая, для которой F’(x) = f(х). Таким образом, неопределенный интеграл определяет все кривые, у которых тангенс угла наклона в каждой ее точке совпадает со значением функции f(х).

Пример:

Построить кривые, которые задаются неопределенным интегралом

Решение:

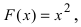
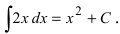
Первообразной для под интегральной функции f(х) = 2х будет функция следовательно, Построим эти кривые (Рис. 1):

Рис. 1. Интегральные кривые

Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна под интегральной функции

Доказательство: По определению неопределенного интеграла

2. Дифференциал неопределенного интеграла равен под интегральному выра- жению

Доказательство: По определению дифференциала от неопределенного интеграла имеем

3. Если под интегральное выражение является дифференциалом некоторой функции F(x), тo неопределенный интеграл равен

Доказательство: Так как

4. Неопределенный интеграл от линейной комбинации функций равен той же самой линейной комбинации неопределенных интегралов от этих функций

5. Формула неопределенного интеграла не зависит от обозначения переменной интегрирования

Таблица основных неопределенных интегралов

Методы интегрирования

Метод тождественных преобразований под интегральной функции

Данный метод основан на использовании простых приемов, алгебраических и тригонометрических формул, свойств подынтегральной функции, разложения полиномов на простые множители и свойств неопределенного интеграла. Рассмотрим этот метод на конкретных примерах.

1. Почленное деление числителя дроби на ее знаменатель

Замечание: Следует запомнить, что нет формулы почленного деления знаменателя дроби на ее числитель, т.е.

Пример:

Найти

Решение:

Выполним в под интегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла

Замечание: Из этого примера видно, что слова «найти неопределенный интеграл” означают: за счет преобразований подынтегральной функции и использования свойств неопределенного интеграла данный интеграл надо привести к совокупности табличных интегралов и воспользоваться этой таблицей.

Замечание: Из примера также видно, что, несмотря на наличие двух табличных интегралов, константа интегрирования С пишется один раз, так как сумма или разность постоянных интегрирования все равно есть постоянная величина.

2. Использование противоположных арифметических операций (например, сложение-вычитание).

Пример:

Найти

Решение:

Анализ под интегральной функции показывает, что в числитель дроби надо добавить и вычесть 1 (при этом подынтегральная функция не изменится), а затем воспользоваться первым приемом (почленное деление числителя дроби на ее знаменатель)

3. Использование алгебраических и тригонометрических формул, например,

и других формул.

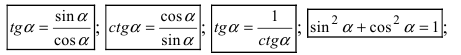
Пример:

Найти

Решение:

Воспользуемся формулой квадрата разности

Пример:

Найти

Решение:

4. Использование свойств функций, например,

Пример:

Вычислить

Решение:

Пример:

Вычислить

Решение:

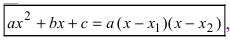
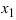
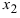
5. Использование разложения полиномов на простые множители, например, , где и корни уравнения

Пример:

Найти

Решение:

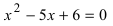
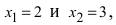
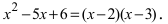
По теореме Виета уравнение имеет корни следовательно, разложение квадратичного полинома на простые множители имеет вид: Подставим полученное выражение в подынтегральную функцию, получим

Метод замены переменной интегрирования

Данный метод основан на формуле

Метод замены переменной интегрирования применяется в двух случаях:

а) Если аргумент функции отличается от простого аргумента х, то этот сложный аргумент принимается в качестве новой переменной интегрирования t.

Пример:

Вычислить

Решение:

Так как показатель степени экспоненты отличается от простого аргумента х, то этот показатель степени принимаем в качестве новой переменной интегрирования, т.е.

Замечание: После нахождения первообразной с новой переменной интегрирования надо обязательно вернуться к старой переменной интегрирования.

Пример:

Вычислить

Решение:

Выражение, стоящее в круглых скобках, является аргументом степенной функции и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е.

Пример:

Вычислить

Решение:

Выражение, стоящее в круглых скобках, является аргументом функции синус и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е. 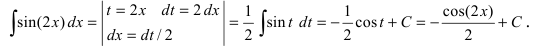б) Если элементарная функция, содержащаяся в подынтегральном выражении, имеет простой аргумент и в качестве множителя при dx присутствует первая производная этой функции, то в качестве новой переменной интегрирования принимается элементарная функция.

Пример:

Найти

Решение:

В подынтегральном выражении содержится элементарная функция tgx и в качестве множителя при dx присутствует ее первая производная 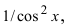следовательно, в качестве новой переменной интегрирования принимаем /gx:

Пример:

Найти

Решение:

Данный пример объединяет первый метод с методом замены переменной интегрирования. Выполним почленное деление числителя дроби на ее знаменатель и разобьем интеграл на два интеграла, для которых применяются два случая замены переменной интегрирования

Замечание: Умение отыскивать подходящую замену вырабатывается в процессе многократных упражнений, однако можно указать ряд случаев, когда можно сразу увидеть необходимую замену переменной интегрирования при анализе подынтегрального выражения, например, 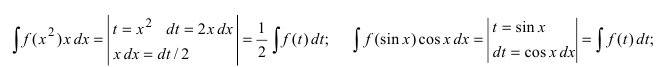Из показанных примеров видно, что умение хорошо интегрировать зависит от хорошего знания таблицы производных от элементарных функций (см. Лекцию № 17 из Первого семестра).

Метод интегрирования по частям

Интегрирование по частям основано на использовании формулы дифференциала от произведения двух функций 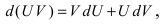откуда находим, что произведение

Таким образом, для неопределенного интеграла формула интегрирования по частям имеет вид:

Для того чтобы знать, какую из функций принимать за U (все остальное в подынтегральном выражении принимается за dV), рассмотрим наиболее часто встречающиеся случаи:

1. — полином (многочлен) порядка n.

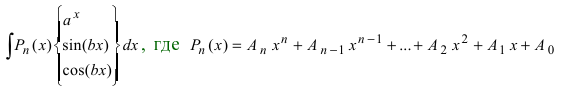
В этом случае

Замечание: Для нахождения функции dU используют определение дифференциала функции. При вычислении функции V интегрируют выражение dV, при этом постоянная интегрирования полагается равной нулю (С = 0). После выполнения этих действий применяют формулу интегрирования по частям.

Пример:

Вычислить

Решение:

Применим метод интегрирования по частям

Замечание: Из приведенного примера видно, что при необходимости метод интегрирования по частям применяется повторно.

2. Для интегралов вида

Пример:

Вычислить

Решение:

Действуя согласно методике, получим

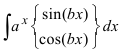
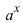
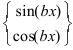
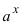
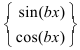
3. Для интегралов вида которые называются возвратными, на первом шаге интегрирования безразлично, какую из функций (показательную или тригонометрическую ) принимать в качестве функции U. Однако на втором шаге в качестве функции U надо обязательно принимать ту из функций (показательную или тригонометрическую ), которая была принята на первом шаге, в противном случае интеграл возвращается к своему исходному виду при отсутствии проинтегрированной части.

Пример:

Найти

Решение:

(если сейчас в качестве функции U выбрать экспоненту, то интеграл вернется к своему первоначальному виду при отсутствии проинтегрированной части; убедитесь в этом самостоятельно)

Решим полученное уравнение относительно буквы Отсюда находим, что

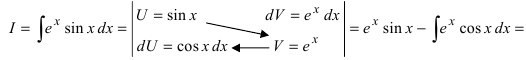
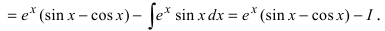
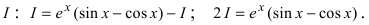
4. Нестандартные интегралы требуют для своего вычисления приобретения опыта на практических занятиях.

Пример:

Найти

Решение:

Неопределенный интеграл

Определение 1. Пусть Δ − промежуток действительной оси. Функция y=F(x) называется первообразной для функции y=f(x) на промежутке Δ, если F(x) − дифференцируема на Δ и 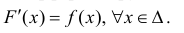(1)

Пример:

а) F(x)=x − первообразная для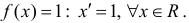
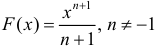
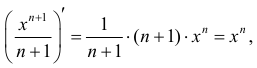
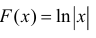
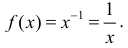
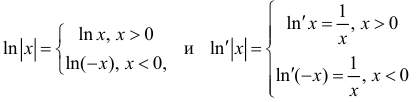
б) − первообразная для − на любом промежутке из области определения функции f(x).
в) − первообразная для Действительно,
− на любом промежутке, не содержащем точку 0.

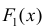
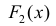
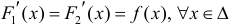
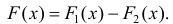
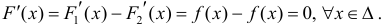
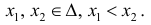
Теорема 1. Две дифференцируемые на промежутке Δ функции и будут первообразными для одной и той же функции y=f(x) тогда и только тогда, когда

. Докажем, что они отличаются на константу. Пусть

Тогда Пусть
По теореме Лагранжа (теорема 4 § 12):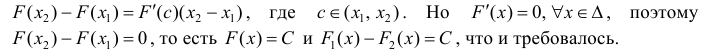

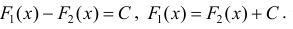
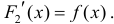
Достаточность. Обозначим
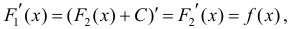
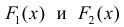
Тогда то есть — первообразные
для одной и той же функции y=f(x), что и требовалось доказать.

Свойства неопределенного интеграла

Свойства 1 – 4 легко выводятся из определения первообразной и интеграла
и соответствующих свойств производной.
Докажем, например, свойство 3.

Из определений 1,2 следует, что интегрирование – действие обратное
дифференцированию (находится функция, производная которой равна данной).

Таблица интегралов

При вычислении интегралов в простых случаях применяют свойства 1 – 4.

Пример:

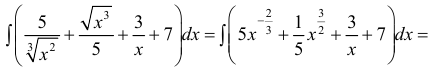
Пример:

Замена переменной в неопределенном интеграле

Пример:

Пример:

Пример:

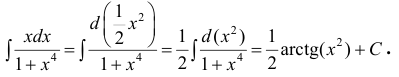
При поднесении под дифференциал можно использовать свойства
дифференциала (см. § 6) 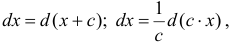где с – константа.

Пример:

Пример:

Пример:

Иногда в формуле (2) легче вычислять левую часть, чем правую:
(5)
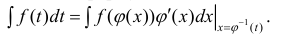
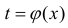
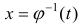
Формула (5) – формула интегрирования с помощью замены переменной ; при этом — обратная функция.

Пример:

Интегрирование по частям в неопределенном интеграле

Пример:

Пример:

Замечание.

Пример:

Пример:

Таким образом, проинтегрировав дважды по частям, получили уравнение,
содержащее 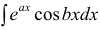в правой и левой части. Решив его, получим:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник