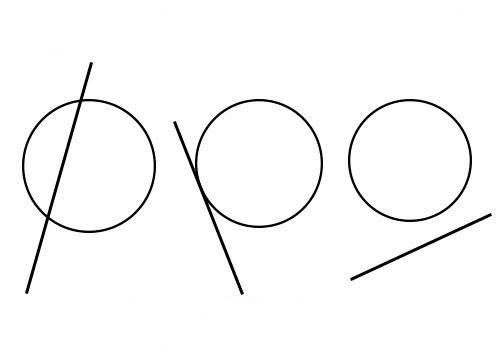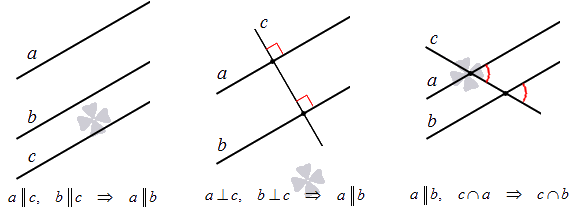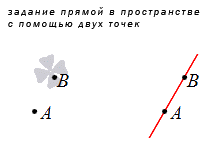Что означает взаимное расположение прямых
Взаимное расположение прямых в пространстве
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями
где — точки, принадлежащие прямым и соответственно, a — направляющие векторы (рис.4.34). Обозначим через вектор, соединяющий заданные точки.
Перечисленным выше случаям взаимного расположения прямых и соответствуют следующие признаки:
– прямые и скрещивающиеся векторы не компланарны;
– прямые и пересекаются векторы компланарны, а векторы не коллинеарны;
– прямые и параллельные векторы коллинеарны, а векторы не коллинеарны;
– прямые и совпадают векторы коллинеарны.
Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:
Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:
– прямые и скрещивающиеся определитель отличен от нуля;
– прямые и пересекаются определитель равен нулю, а вторая и третья его строки не пропорциональны, т.е.
– прямые и параллельные вторая и третья строки определителя пропорциональны, т.е. а первые две строки не пропорциональны, т.е.
– прямые и совпадают все строки определителя пропорциональны, т.е.
Расстояние между параллельными прямыми
Найдем расстояние между параллельными прямыми, заданными каноническими уравнениями (рис.4.35)
где — произвольные точки на прямых и соответственно, а координаты направляющих векторов прямых пропорциональны:
Расстояние между скрещивающимися прямыми
Напомним, что расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра, т.е. кратчайшее расстояние между точками этих прямых.
Найдем расстояние между скрещивающимися прямыми, заданными каноническими уравнениями
где — произвольные точки на прямых и соответственно.
Искомое расстояние равно высоте параллелепипеда, построенного на векторах (рис.4.36), т.е.
— смешанное и векторное произведения векторов. Как показано выше, прямые и скрещивающиеся тогда и только тогда, когда векторы некомпланарные, т.е.
Отсюда следует, что вторая и третья строки не пропорциональны. Поэтому векторы неколлинеарные, т.е. и знаменатель в правой части (4.38) отличен от нуля.
Угол между прямыми
Угол между прямыми определяется как угол между их направляющими векторами. Поэтому величина острого угла между прямыми
вычисляется по формуле
Решение. Каноническое уравнение оси абсцисс имеет вид так как ось проходит через точку а — ее направляющий вектор. Каноническое уравнение прямой получено в примере 4.15,»а»:
Полагая по формуле (4.38) получаем:
Острый угол находим по формуле (4.39):
Взаимное расположение прямой и плоскости
Возможны три случая взаимного расположения прямой и плоскости:
– прямая и плоскость пересекаются, т.е. имеют одну общую точку;
– прямая и плоскость параллельны, т.е. не имеют общих точек;
– прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.
Получим признаки для всех этих случаев. Пусть прямая и плоскость заданы уравнениями:
т.е. прямая проходит через точку коллинеарно вектору а плоскость перпендикулярна вектору
Перечисленным выше случаям взаимного расположения прямой и плоскости соответствуют следующие признаки:
– прямая и плоскость пересекаются векторы и не ортогональны (рис.4.37,а);
– прямая и плоскость параллельны векторы и ортогональны, а точка не принадлежит плоскости (рис.4.37,б);
– прямая лежит в плоскости векторы и ортогональны, а точка принадлежит плоскости (рис.4.37,в).
Учитывая свойство скалярного произведения векторов получаем:
– прямая и плоскость пересекаются ;
– прямая и плоскость параллельны
– прямая лежит в плоскости
Угол между прямой и плоскостью
Отсюда, например, следует полученное ранее необходимое условие параллельности прямой и плоскости.
Взаимное расположение прямых в пространстве. Взаимное расположение точки и прямой
Базовыми геометрическими элементами являются точка, прямая и плоскость. Они называются так потому, что из них можно построить многие объекты, например, такие как пирамида или призма. Чтобы понять свойства этих фигур, важно знать взаимное расположение в пространстве прямых и плоскостей. Рассмотрим подробнее этот вопрос в статье.
Определение и описание точки, прямой и плоскости

(x; y; z) = (x0; y0; z0) + α*(a; b; c)
Элементы с нулевыми индексами соответствуют некоторой точке, которая является частью прямой. Координаты, которые умножаются на параметр α (альфа) описывают ее направляющий вектор, вдоль которого она проходит. Подставляя произвольные числа α можно найти все точки, которые образуют прямую в пространстве.
Очевидно, что для векторного уравнения в двумерном пространстве необходимо использовать лишь две координаты для точек и векторов.
Плоскость является совокупностью точек. Образованные на них вектора перпендикулярны некоторому направлению, задаваемому нормальным к плоскости вектором. Все это можно описать несколькими способами. Тем не менее, для решения задач на определение взаимного расположения плоскости и прямой удобно пользоваться уравнением общего вида. Оно записано ниже:
Удобство этой формы записи заключается в том, что коэффициенты A, B, C являются координатами перпендикулярного вектора n¯ к плоскости.
При решении задач важно учитывать, в каком пространстве решается проблема. Так, приведенный вид уравнения плоскости в двумерном случае без координаты z будет соответствовать уравнению прямой.
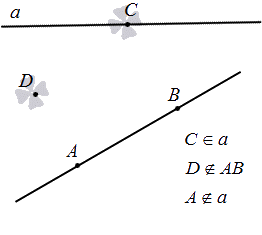
Расположение точки и прямой

Взаимное расположение этих объектов не зависит от того, рассматриваются они на плоскости или в пространстве. Критерии определения постоянно одни и те же.
Относительно прямой точка может находиться лишь в двух возможных положениях:
Определить вариант расположения в конкретной задаче достаточно легко. Для этого следует подставить координаты искомого объекта в уравнение, задающее прямую. Если равенство будет выполняться, значит, точка принадлежит прямой. В противном случае она не является ее частью.
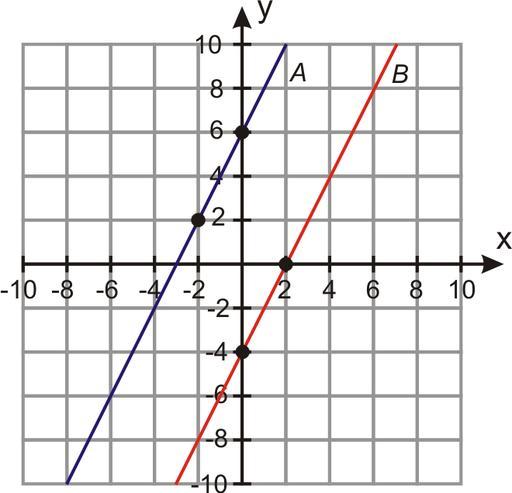
Две прямые на плоскости
Какое может быть взаимное расположение двух прямых на плоскости? Существует три разных варианта:
Чтобы понять, каково взаимное расположение прямых в конкретном случае, необходимо провести некоторый математический анализ. Ниже описываются основные идеи, которые следует использовать при его осуществлении.
Если направляющие векторы прямых параллельны друг другу, значит и прямые, как минимум, будут параллельными. Параллельность векторов доказывается, если один из них можно представить в виде другого, умноженного на действительное число.
Если направляющие вектора параллельны, и хотя бы одна точка одной прямой соответствует и другой прямой, тогда речь идет о полностью совпадающих прямых.
Если направляющие вектора не являются параллельными, то прямые пересекаются в одной точке. Найти ее координаты можно с помощью решения системы уравнений (эти координаты должны соответствовать обоим уравнениям прямых).
Частным случаем пересечения прямых является угол пересечения, равный 90o. В таком случае говорят о перпендикулярности между рассматриваемыми объектами. Если две прямые перпендикулярны, то скалярное произведение их векторов направляющих будет равно нулю.
Прямая и окружность на плоскости
Поскольку данный объект часто появляется в геометрических задачах, то полезно также рассмотреть вопрос взаимного расположения окружности и прямой. Возможны такие варианты:
Определить вариант расположения этих объектов для конкретной задачи можно с использованием соответствующих уравнений. Для окружности с центром в (x0; y0) и радиусом R оно имеет вид:
Определение варианта расположения сводится к решению квадратного уравнения.
Две прямые в пространстве
Расчет расстояния производится по формуле:
Формулу можно непосредственно применить, если даны векторные уравнения прямых.
Плоскость и прямая
В данном случае речь идет о трехмерном пространстве. Взаимное расположение плоскости и прямой возможно следующее:
Определить параллельность этих геометрических объектов достаточно просто. Для этого нужно рассчитать скалярное произведение нормального вектора плоскости и направляющего вектора прямой. Равенство нулю этого произведения является достаточным условием параллельности. Если к тому же хотя бы одна точка принадлежит плоскости, значит, вся прямая лежит в ней.
Если скалярное произведение нулю не равно, тогда вывод следующий. Прямая и плоскость пересекаются в одной точке. Частным случаем является пересечение под прямым углом. Если направляющий вектор прямой можно представить в виде произведения на число вектора нормали к плоскости, значит, прямая и плоскость перпендикулярны.
Задача с двумя прямыми на плоскости
Ниже даны два уравнения в общем виде для прямых в двумерном пространстве:
Необходимо определить взаимное расположение прямых.
Поскольку имеет место случай на плоскости, то нет необходимости приводить эти уравнения к векторному виду. Решить задачу можно проще, если найти корни системы из этих них. Имеем:
Поскольку система имеет единственное решение, то оно соответствует пересечению рассматриваемых прямых в точке (14; 21).
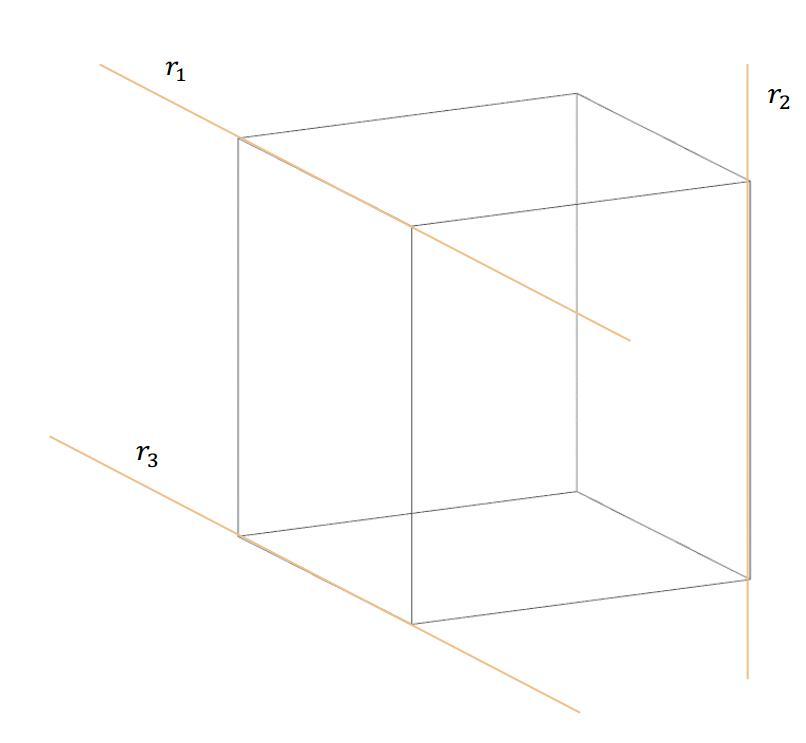
Задача с двумя прямыми в пространстве
Даны две прямые, которые описываются уравнениями:
Каково взаимное расположение прямых в пространстве?
Можно заметить, что направляющие вектора параллельными не являются (никакое значение параметра β не способно дать направляющий вектор r1). То есть прямые либо пересекаются, либо являются скрещивающимися.
Его векторное произведение с направляющим вектором для r1 равно:
Поскольку длина этого вектора отлична от нуля, значит, расстояние между прямыми будет больше нуля. Последний факт говорит, что они не имеют общих точек и являются скрещивающимися.
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Прямая на плоскости – необходимые сведения
Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.
Прямая на плоскости – понятие
Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.
Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.
Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.
Взаимное расположение прямой и точки
На каждой прямой и в каждой плоскости могут быть отмечены точки.
Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.
Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.
Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:
Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.
Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.
Точка делит прямую на две части, называемые лучами. Имеем аксиому:
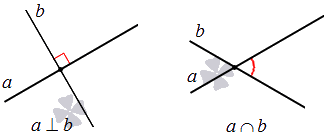
Взаимное расположение прямых на плоскости
Расположение прямых на плоскости может принимать вид двух состояний.
Две прямые на плоскости могут совпадать.
Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.
Две прямые на плоскости могут пересекаться.
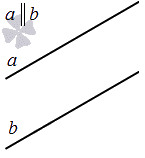
Две прямые на плоскости могут быть параллельны.
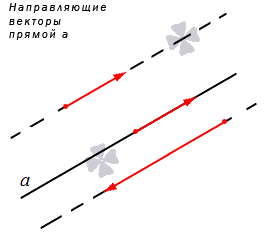
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.
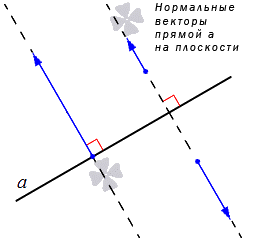
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.
Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.
Для этого приводим необходимы факторы, доказывающие их взаимное расположение:
Рассмотрим это на рисунках.
Способы задания прямой на плоскости
Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.
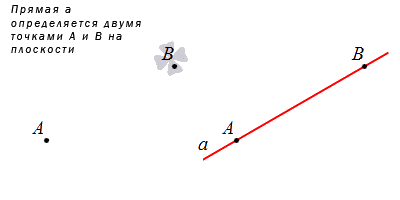
Прямая задается при помощи указанных двух точек, расположенных в плоскости.
Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.
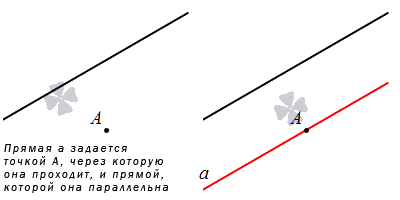
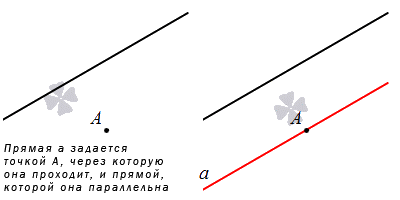
Прямая может быть задана через точку и прямую, которой она параллельна.
Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.
Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.
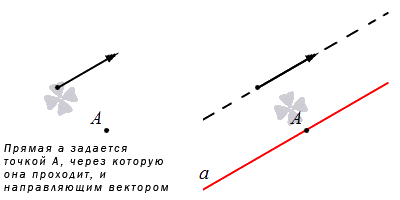
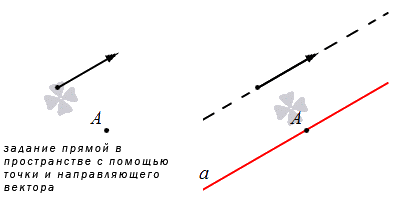
Прямая задается через указанную точку и направляющий вектор.
Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:
Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.
И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.
Прямая в пространстве – необходимые сведения
Статья рассказывает о взаимном расположении линий в пространстве. Будут рассмотрены основные способы задания прямой с приведением примеров и наглядных рисунков.
Прямая в пространстве – понятие
Раздел о прямой на плоскости дает представление о течки и прямой. Расположение прямой в пространстве аналогично. Если мысленно отметить две точки и провести линию, соединив их, получим прямую, уходящую в бесконечность.
Точки, прямые и отрезки в пространстве обозначаются аналогично расположению в плоскости.
Если прямая располагается на плоскости в пространстве, тогда это можно подкрепить аксиомами:
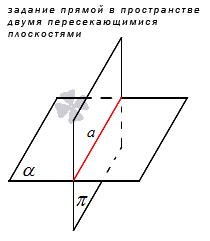
Имеет место аксиома, благодаря которой можно рассматривать прямую в пространстве в качестве двух пересеченных плоскостей:
Если две плоскости имеют общую точку, тогда имеют общую прямую, на которой лежат все общие точки этих плоскостей. Показано на рисунке, приведенном ниже.
Взаимное расположение прямых в пространстве
Две прямые, расположенные в пространстве, могут пересекаться в случае наличия одной общей точки.
Данный случай говорит о том, что прямые располагаются на плоскости трехмерного пространства. Когда прямые, расположенные в пространстве, пересекаются, то переходим к определению угла между пересекающимися прямыми.
Две прямые пространства параллельны в том случае, если расположены в одной плоскости без общих точек.
Рассмотрим ниже расположение параллельных прямых.
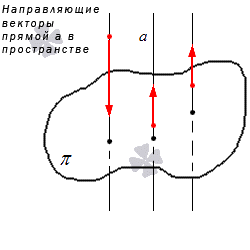
После рассмотрения определения параллельных прямых, расположенных в пространстве, необходимо добавить о направляющих векторах прямой.
Ненулевой вектор, который располагается на прямой или на параллельной ему прямой, называют направляющим вектором данной прямой.
Если по условию дана линия в пространстве, то он используется для решения задач.
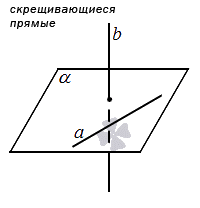
Две прямые пространства могут быть скрещивающимися.
Две прямые называют скрещивающимися, при условии, что они лежат в одной плоскости.
Это тесно связано с определением угла между скрещивающимися прямыми.
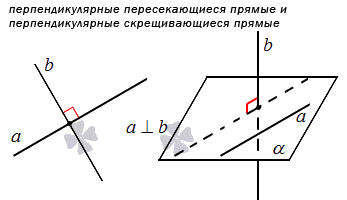
Особым случаем считается пересечение или скрещивание прямых под прямым углом в пространстве. Их называют перпендикулярными. Рассмотрим на рисунке.
Способы задания прямой в пространстве
Для того, чтобы расположить прямую в пространстве, существует несколько методов.
Из аксиомы для двух точек плоскости имеем, что через них может быть задана единственная прямая. При расположении двух точек в пространстве также задается только одна прямая, проходящая через них.
При прямоугольной системе координат прямая задается с помощью координат точек, которые располагаются в трехмерном пространстве. Это и позволяет составить уравнение прямой, проходящей через две заданные точки.
Еще один способ задания прямой – это теорема. Через любую точку пространства, не лежащую на данной прямой, может проходить прямая, параллельная данной, причем только одна.
Отсюда следует, что при задавании прямой и точки, не лежащей на ней, сможем определить прямую, которая параллельна заданной и проходит через указанную точку.
Есть способ, когда можно указать точку, направляющий вектор и прямую, которая проходит через нее. При задании прямой относительно прямоугольной систему координат, можно говорить о канонических и параметрических уравнениях прямой в пространстве.
Немаловажный способ задания прямой – это способ, основанный на аксиоме: если две плоскости имеют общую точку, тогда имеют общую прямую, где располагаются общие точки заданных плоскостей. При задании двух пересекающихся плоскостей можно определить прямую пространства.
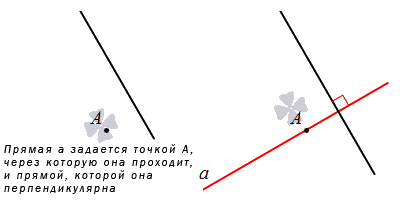
Если задана плоскость и нележащая в ней точка, тогда существует прямая, проходящая через нее и перпендикулярная заданной плоскости, причем только одна. Этот способ задания базируется на теореме. Получаем, что для определения прямой достаточно задать плоскость, перпендикулярную ей, с точкой, через которую проходит заданная прямая.
В случае, если прямая задается относительно введенной прямоугольной системы координат, то следует укрепить знания из статьиуравнения прямой, проходящей через заданную точку перпендикулярно в заданной плоскости.Рассмотрим задание прямой, используя точку, через которую она пройдет, и плоскости, которая располагается перпендикулярно относительно заданной прямой.