Что означает запись 10 в 5 степени
Таблица степеней
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Степень числа с натуральным показателем — это результат многократного умножения числа на себя. Само число называют основанием степени, а количество операций умножения — показателем степени.
Запись читается, как «a» в степени «n».
Вот пример для наглядности:
Эту запись можно прочитать тремя способами:
Свойства степеней
Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.
Подготовка к ЕГЭ по математике онлайн поможет снять стресс перед экзаменом и повысит шансы на высокий балл.
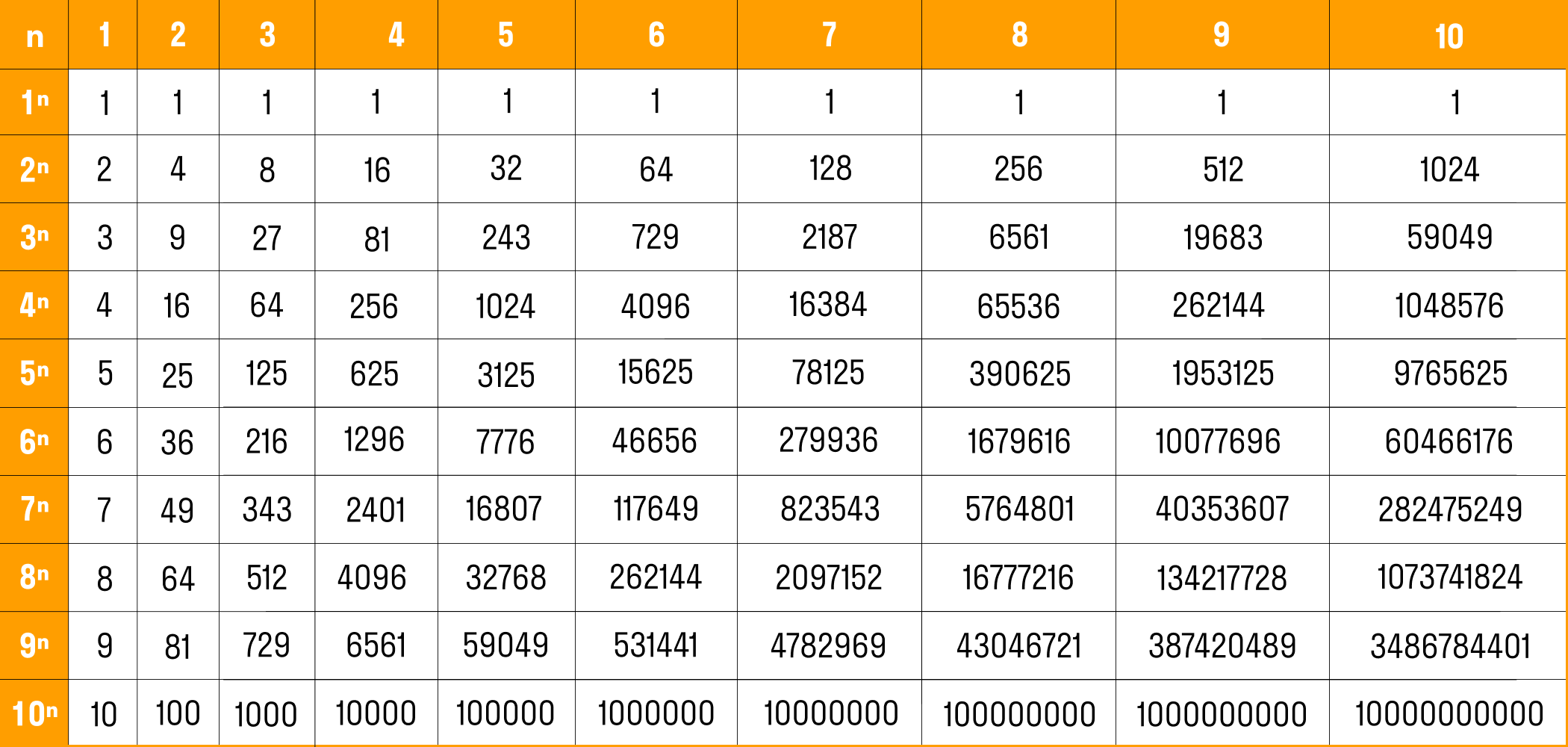
Таблица степеней от 1 до 10
Таблица степеней — это перечень чисел от 1 до 10, возведенных в степень от 1 до 10. Ниже приведены два вида таблиц: выберите ту, которая удобнее для вас, скачайте на телефон или распечатайте и положите в учебник.
Как найти необходимые значения в этой таблице:
В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.
А если ответ нужно получить как можно быстрее, можно использовать онлайн-калькулятор степеней.
Решение задач
5 2 × 5 3 = 5 2+3 = 5 5 = 3125
2 4 × 3 3 × 2 5 = 2 4+5 × 3 3 = 2 9 × 3 3 = 512 × 27 = 13 824
При условии, что у нас есть только таблица до 10, разложим основание степени на множители:
Свойства степеней. Действия со степенями
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Таблица степеней
Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.
Калькулятор степеней
С помощью данного калькулятора вы сможете в режиме онлайн вычислить степень любого натурального числа. Введите число, степень и нажмите кнопку «вычислить».
Таблица степеней от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4 n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5 n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6 n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7 n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8 n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9 n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10 n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
10 10 = 10000000000
Теория
запись читается: «a» в степени «n».
4 6 = 4 × 4 × 4 × 4 × 4 × 4 = 4096
Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.
Урок по математике 5класс «Степень числа»
Сценарии уроков по учебнику «Математика, 5 класс», часть 1
Тема: «Степень числа».
1) сформировать понятие степени, способность к чтению и записи выражений со степенями;
2) повторить и закрепить смысл умножения натуральных чисел, понятия простого и составного числа, зависимость между компонентами и результатами арифметических действий, тренировать вычислительные навыки, способность к анализу и решению задач
1) задания для актуализации знаний:
3; 3·3; 3·3·3; 3·3·3·3; 3·3·3·3·3…







 а + а + … + а = а · n
а + а + … + а = а · n


 5 1980 2 · 5
5 1980 2 · 5