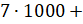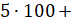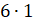Что означает запишите десятичной записью число
ВОПРОСЫ
1. Сколько знаков используют для записи натуральных чисел в десятичной системе? Как называют эти знаки?
Для записи натуральных чисел в десятичной системе используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти знаки называют цифрами.
2. Какие натуральные числа называют однозначными? Двузначными? Трёхзначными? Многозначными?
3. Какая цифра не может стоять первой в записи натурального числа?
В записи натурального числа первой не может стоять цифра 0.
4. Как называют группы по три цифры, на которые разбивают многозначные числа справа налево?
5. Назовите по порядку первые четыре класса в записи натуральных чисел.
6. Сколько разрядов имеет каждый класс? Как их называют?
7. Как называют запись натурального числа, которой мы пользуемся?
Запись натурального числа, которой мы пользуемся, называют десятичной.
8. С чем связано название десятичной записи натуральных чисел?
РЕШАЕМ УСТНО
1. На сколько:
1) 18 больше 6 на 12
2) 4 меньше 12 на 8
2. Во сколько раз:
1) 18 больше 6 в 3 раза
2) 4 меньше 12 в 3 раза
3. Вычислите:
4. Назовите пять последовательных натуральных чисел, начиная с числа: 1) 423; 2) 1658; 3) 2997.
1) 432, 424, 425, 426, 427
2) 1658, 1659, 1660, 1661, 1662
3) 2997, 2998, 2999, 3000, 3001
5. Назовите в обратном порядке пять последовательных натуральных чисел, начиная с числа: 1) 358; 2) 1573; 3) 4001.
1) 358, 357, 356, 355, 354
2) 1573, 1572, 1571, 1570, 1569
3) 4001, 4000, 3999, 3998, 3997
6. Назовите все четырехзначные числа, сумма цифр которых равна 2.
1001, 1010, 1100, 2000
7. Двузначное число оканчивается цифрой 4. Если к этому числу прибавить число, записанное теми же цифрами, но в обратном порядке, то получим число 99. Найдите эти два числа.
54 и 45
УПРАЖНЕНИЯ
17. Назовите разряд, в котором стоит цифра 4 в записи числа:
18. Прочитайте число:
1) 234642
2) 502013
3) 9145679
4) 105289001
5) 6704917320
6) 72016050400
7) 491872653000
8) 305002800748
19. Запишите десятичной записью число:
20. Запишите десятичной записью число:
21. Запишите десятичной записью число:
22. Запишите десятичной записью число:
23. Запишите десятичной записью число:
24. Запишите и прочитайте число, которое образуется, если записать число 514 подряд: 1) два раза; 2) три раза; 3) четыре раза.
25. Запишите и прочитайте число, которое образуется, если записать число 48 подряд: 1) два раза; 2) три раза; 3) четыре раза; 4) пять раз.
26. Запишите в виде суммы разрядных слагаемых число:
27. Запишите в виде суммы разрядных слагаемых число:
28. Запишите число, которое:
1) на 1 меньше наименьшего трехзначного числа
2) на 4 больше наибольшего трехзначного числа
3) на 5 меньше наименьшего пятизначного числа
4) на 6 больше наибольшего шестизначного числа
5) на 7 больше наименьшего восьмизначного числа
1) 99
2) 1 003
3) 9 995
4) 1 000 005
5) 9 999 993
29. Запишите наибольшее восьмизначное число, а также следующее и предыдущее числа.
Наибольшее восьмизначное число 99 999 999Следующее за ним 100 000 000, предыдущее 99 999 998
30. Запишите наименьшее семизначное число, а также следующее и предыдущее числа.
Наибольшее семизначное число 9 999 999Следующее 10 000 000, предыдущее 9 999 99831.
31. Двузначное число записали подряд два раза. Во сколько раз полученное четырехзначное число больше данного двузначного числа?
32. Трехзначное число записали подряд два раза. Во сколько раз полученное шестизначное число больше данного трехзначного числа?
33. В книге пронумерованы страницы с первой по сто семьдесят вторую. Сколько цифр напечатано при нумерации страниц?
34. Для нумерации страниц книги напечатано 2 004 цифры. Сколько страницв этой книге?
35. Каких трехзначных чисел больше: все цифры которых четные или все цифры которых нечетные?
Нечетных цифр больше, чем четных, значит больше трехзначных чисел, состоящих их нечетных чисел.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
36. Вычислите:
37. Выполните действия:
1961+8+31=2000 (-м году начала работать МКС)
2017-2000=17 (лет работают космонавты)
60+60:12=60+5= 65 (пудов)
24+24*3=24+72 = 96 (пиявок)
41. Вертолет за 4 ч может пролететь 720 км. Какое расстояние от пролетит за 6 ч с той же скоростью?
720:4*6 = 1090 (км пролетит за 6 часов)
42. За три дня кузнец Вакула изготовил 432 подковы. Сколько подков он изготовит за пять дней, работая с такой же производительностью?
ЗАДАЧА ОТ МУДРОЙ СОВЫ
43. В этом году день рождения отца был в воскресенье. В какой день неделеи праздновала свой день рождения мать, если она на 62 дня моложе отца.
62-8*7 = 62-56 = 6 (дней)
От воскресенья отсчитает 6 дней назад, получим понедельник.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Запись чисел в десятичной системе счисления
Десятичной записью натурального числа x называется его представление в виде: 
Сумму 

Так как понятие числа и его записи нетождественны, то существование и единственность десятичной записи натуральной записи надо доказывать.
Десятичная запись числа позволяет просто решать вопрос о том, какое из них меньше.
Пусть х и у – натуральные числа, запись которых дана в десятичной системе счисления:


Тогда число х меньше числа у, если выполнено одно из условий:
а) n Просмотров 23 670 Комментариев 0
Математика. 5 класс
Конспект урока
Ряд натуральных чисел. Десятичная система записи натуральных чисел
Перечень вопросов, рассматриваемых в теме:
— десятичная запись натуральных чисел;
— разрядность натуральных чисел
Натуральные числа – числа, которые используют при подсчёте предметов.
Натуральный ряд – последовательность всех натуральных чисел, расположенных в порядке возрастания.
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Теоретический материал для самостоятельного изучения
С древних времен у человека была потребность в счёте.
Числа, которые используют при подсчёте предметов, называют натуральными числами.
Таким образом, числа: один, два, три, …, десять, …, сто, …, тысяча, …, миллион и так далее – это натуральные числа.
Натуральные числа один, два, три, четыре, пять и так далее, записанные в порядке возрастания и без пропусков, образуют ряд натуральных чисел.
Стоит отметить, что самое маленькое натуральное число – единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нём нет.
В настоящее время принята десятичная система записи чисел (десятичная система счисления), в которой числа записываются при помощи десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – эти знаки называют цифрами.
Одна и та же цифра может иметь различное значение в зависимости от позиции, где она расположена в записи числа. Например, в записи числа пятьсот пятьдесят пять первая справа цифра пять означает пять единиц, вторая – пять десятков, третья – пять сотен.
Вот поэтому десятичную систему счисления называют позиционной.
Натуральные числа, записанные одной цифрой, называют однозначными, а записанные несколькими цифрами – многозначными: двумя – двузначными, тремя – трёхзначными и т. д.
Например, числа 1, 8, 9 – однозначные числа; 10, 66, 89 – двузначные числа; 111, 145 – трёхзначные числа; 123456 – шестизначное число.
Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называются классами.
Первый класс справа называют классом единиц, второй – классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов и т. д.
Цифры. Десятичная запись натуральных чисел
Урок 2. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Цифры. Десятичная запись натуральных чисел»
Давайте представим себе такую историю…
– 2, 0, 1, 7, 2, 0, 1, 7, 2, 0, 1, – бурчал себе под нос Саша.
– Чем это ты тут занимаешься? – спросил Паша.
– Хочу научиться красиво писать цифры, – ответил Саша.
– Саша, смотри, какое интересное число у тебя получилось, – провозгласил Паша. – А ты можешь его прочитать? – спросил он у Саши.
– Прочитать! Конечно! – взбодрился Саша. – Что тут сложного? 2, 0, 1, 7, 2, 0…
– Нет, Саша! – перебил Паша. – Ты просто перечисляешь записанные цифры, а назвать число – это совсем по-другому. Вот как ты думаешь, что общего между буквами и цифрами?
– Не знаю, – прозвучал ответ Саши. – Может, только если одни и другие мы учим в школе?
– Ну почти! – сказал Паша. – Буквы и цифры – это знаки, которые придумали для записи. Так, например, из букв можно записать слово, а вот из цифр – число. У тебя из цифр тоже получилось число, которое имеет своё имя.
– Правда? – удивился Саша. – И как же его зовут?
– Ты знаешь, я немного забыл, как правильно его назвать, – стушевался Паша. – Но я точно знаю, кто нам может помочь!
– Ребята, прежде, чем я вам поведаю свой рассказ о цифрах, числах и ещё кое о чём интересном, хочу, чтобы вы немного размялись и выполнили устные задания, – предложил Электроша.
– Давайте сверимся! – сказал Электроша. – Посмотрите, что у вас должно было получиться!
– Ну а теперь давайте поговорим о числах, – предложил Электроша. – Вы уже знаете, что в алфавите русского языка существует 33 буквы и из них можно составить огромное множество слов.
Цифры в математике выполняют такую же роль, как и буквы в русском языке. Только из цифр составляют различные числа.
Правда, цифр гораздо меньше, чем букв. Их всего лишь 10:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
– Так мало? –удивился Саша.
– Цифр-то мало, а вот составить из них чисел можно сколько угодно! – продолжил Электроша.
– А вы знаете, что цифры изобрели давным-давно? – спросил у мальчиков Электроша. Это произошло в Индии ещё в VI веке. Правда, сами цифры принято называть арабскими.
– Арабскими? – удивился Паша. – Но ведь ты же сказал, что цифры придумали в Индии? А значит, их нужно называть индийскими!
– Всё правильно Паша! – улыбнулся Электроша, – придумали то их в Индии, но к нам цифры пришли от арабов, которые подсмотрели их у индийцев, поэтому-то их и стали называть арабскими.
– А теперь поговорим о том, как называют числа! – продолжил Электроша. От количества цифр (знаков) в числе зависит его название. Так, например, если число состоит из одной цифры, то его называют однозначным.
– Такое смешное название! – ухмыльнулся Саша.
– Да, да, одна цифра – один знак, поэтому и однозначное, – продолжил Электроша. –Самое маленькое однозначное натуральное число – 1, а самое большое – 9.
Кроме однозначных чисел, есть и многозначные. Если число состоит из двух цифр, то его называют двузначным числом.
– Вот вы, мальчики, можете назвать самое маленькое и самое большое двузначное натуральное число? – спросил Электроша.
– Конечно! – обрадовались мальчишки. – Это же легче лёгкого!
– Самое маленькое двузначное число – это 10, – сказал Паша.
– Верно! – подтвердил Электроша.
– А вот самое большое двузначное число – это 90! – воскликнул Саша.
– Нет, нет, – исправил Сашу Электроша. Самое большое двузначное число – 99. А вот следом за ним уже идёт наименьшее трёхзначное натуральное число – 100. Число сто записано тремя цифрами, поэтому его называют трёхзначным.
Запомните! Многозначное число может начинаться с любой цифры, кроме цифры ноль.
Каждая цифра в записи многозначного числа занимает определённое место – позицию.
– Что это значит – определённое место? – решил спросить Саша.
– Перед вами три трёхзначных числа, – продолжил Электроша. – Посмотрите: в их записи участвуют одни и те же цифры.
– Но ведь сами числа же различны, – возразил Паша. – В них цифры стоят на разных местах.
– Ты правильно заметил, Паша, – сказал Электроша. – В записи числа важно то, какую позицию занимает цифра, то есть на каком месте она стоит.
Место, на котором стоит цифра в записи числа, по-другому называют разрядом числа. Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.
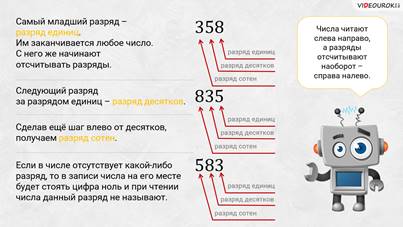
– Да, да, я вспомнил, – радостно сказал Паша, – нам в школе рассказывали. Вот если взять, например, число 358, то у него цифра 8 относится к разряду единиц, цифра 5 – к разряду десятков, а вот цифра 3 – к разряду сотен.
– Всё правильно, Паша! – подбодрил мальчика Электроша. Самый младший разряд – разряд единиц. Им заканчивается любое число. С него же начинают отсчитывать разряды.
Обратите внимание: числа читают слева направо, а разряды отсчитывают наоборот – справа налево. Итак, первый – это разряд единиц. Следующий за ним разряд – разряд десятков. Сделав ещё шаг влево от десятков, получаем разряд сотен.
Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра 0 и при чтении числа данный разряд не называют.
– Мы с Сашей хотели прочитать число, которое у него получилось, – перебил Паша. – Посмотри, какое большущее число у него вышло.
– Ребята, прочитать это число совсем не сложно, – сказал Электроша. – Сейчас я вам покажу, как это сделать.
Итак, чтобы прочитать многозначное число, цифры его записи нужно мысленно разбить справа налево на группы по три цифры в каждой, при этом крайняя слева группа цифр может состоять необязательно только из трёх цифр, в ней могут быть две, как в нашем числе, или даже одна цифра. Эти группы называют классами.
– Классами? – уточнил Саша. Ты ничего не путаешь, Электроша? В классах учатся в школе. Числа же не учатся в школе.
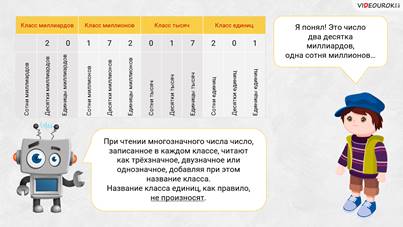
– Именно классами! – улыбнулся Электроша. – Многозначные числа разбивают на классы для удобства их чтения и записи. Единицы, десятки, сотни образуют первый класс – класс единиц. Следующие три цифры числа образуют соответственно разряды: единицы тысяч, десятки тысяч, сотни тысяч. Единицы тысяч, десятки тысяч и сотни тысяч образуют второй класс – класс тысяч. Если мы продвинемся ещё дальше влево, то обнаружим ещё три разряда: единицы миллионов, десятки миллионов и сотни миллионов. Единицы миллионов, десятки миллионов, сотни миллионов образуют третий класс – класс миллионов. Следующие три цифры числа образуют соответственно разряды: единицы миллиардов, десятки миллиардов и сотни миллиардов, а вместе они составляют четвёртый класс – класс миллиардов.
– Я понял, как назвать моё число! – вскрикнул Саша. – Это число два десятка миллиардов, одна сотня миллионов…
– Нет, Саша! – перебил мальчика Электроша. – Ты не до конца понял.
При чтении многозначного числа число, записанное в каждом классе, читают как трёхзначное, двузначное или однозначное, добавляя при этом название класса. Только вот название класса единиц, как правило, не произносят.
– А, понятно, – обрадовался Саша. – Значит, в моём числе 20 миллиардов?
– Правильно! – сказал Электроша. – Может, ты сможешь назвать всё число?
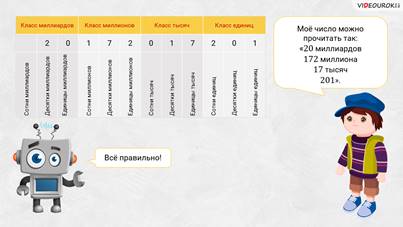
– Я попробую, – ответил Саша. – Моё число, – продолжил он, – можно прочитать так: 20 миллиардов 172 миллиона 17 тысяч 201.
– Всё правильно, Саша! – сказал Электроша. – С чтением многозначного числа ты справился на отлично. Ещё вам с Пашей полезно будет узнать, как правильно записывать многозначные числа.
Чтобы записать многозначное число, вам пригодятся следующие правила:
1. Многозначные числа записывают слева направо и начинают со старшего разряда.
2. Во всех классах, кроме старшего, должно быть по три цифры.
3. Для удобства чтения между классами можно оставить небольшой промежуток.
4. Если отсутствуют единицы какого-либо разряда, вместо них пишут нули.
5. Если отсутствует целый класс, то вместо него пишут три нуля.
– Ребята, давайте вы попробуете сами записать многозначное число! – предложил Электроша. – Слушайте внимательно число: двадцать три миллиона пять тысяч двадцать три.
– Какие вы молодцы! – обрадовался за ребят Электроша. – Всё правильно написали!
А ещё вот что вам нужно знать, – продолжил он. – Запись натуральных чисел, которой мы пользуемся, называют десятичной. Такое название связано с тем, что 10 – это основа десятичной нумерации. Самое главное для вас сейчас – это понять, что десять единиц одного разряда образуют одну единицу следующего за ним разряда. Например, 10 единиц составляют 1 десяток, в свою очередь, 10 десятков – 1 сотню и так далее.
Числа 10, 100, 1000 и так далее называют разрядными единицами.
Зная это, вы сможете любое натуральное число представить в виде суммы разрядных слагаемых. К примеру, возьмём число 8 543. Его можно записать суммой разрядных слагаемых так:
8 543 = 8 000 + 500 + 40 + 3.
Или вот так: 8 543 = 8 · 1 000 + 5 · 100 + 4 · 10 + 3.
Последнее равенство называют записью числа 8 543 в виде суммы разрядных слагаемых.
– А теперь, ребята, давайте посмотрим, как вы всё поняли и выполним несколько заданий.
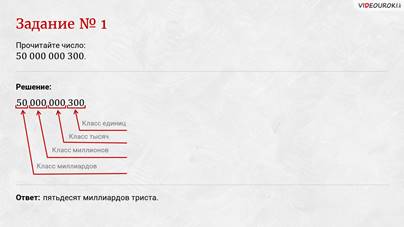
Задание первое: прочитайте число 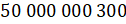
Решение: мысленно делим наше число на группы по три цифры начиная справа. Три первых цифры составляют класс единиц, три следующих – класс тысяч, ещё три следом – класс миллионов и последние – класс миллиардов. Видим, что в классе миллионов и классе тысяч стоят нули, значит, в этих классах отсутствуют единицы в разрядах. Тогда указанное число – пятьдесят миллиардов триста.
Следующее задание: запишите цифрами число пять миллионов одиннадцать тысяч шестьсот один.
Решение: число пишем слева направо. Старший класс в нашем числе – миллионы, и их пять, значит, записываем цифру 5. Следующий класс – тысячи. Сказано, что в числе их одиннадцать, значит, отсутствует разряд сотен и вместо него мы запишем цифру 0. За ней ставим 11. И последний класс в этом числе – класс единиц, их 601, разряд десятков отсутствует, на его месте ставим цифру 0.
И последнее задание: запишите число 7 506 в виде суммы разрядных слагаемых.
Решение: у нас в числе семь тысяч, значит, пишем