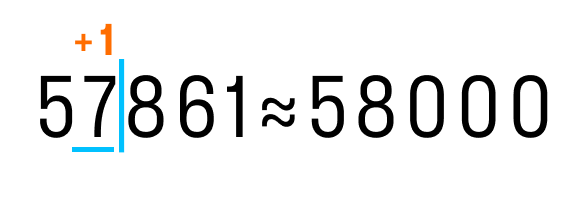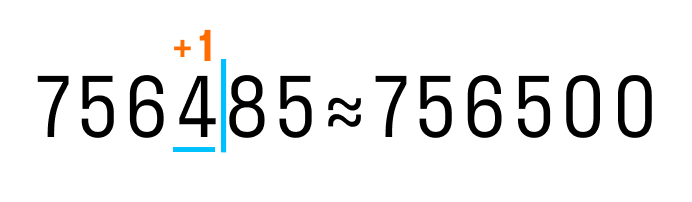Что означает запятая после цифры
Как читать десятичные дроби
В первую очередь обсудим вид десятичной дроби. Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше. Чтобы правильно прочитать десятичную дробь нужно:
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится целая часть десятичной дроби. Читаем: «сорок три целых».
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней правой цифры отличной от нуля можно добавлять сколько угодно нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим такую же по значению десятичную дробь.
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля цифры. Нули между цифрами в числе убирать нельзя.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Как правильно округлять числа после запятой
Далеко не все умеют округлять числа правильно. Например, купив товар за 1469 рублей, чаще всего люди говорят, что потратили полторы тысячи. В целом это так, но некоторые правила округления нарушаются. Чтобы этого избежать, мы с вами поговорим о том, как правильно работать с числами.
Зачем нужно округление
Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.
Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:
Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.
Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.
Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.
Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.
Правила округления чисел
В основе округления лежат математические правила:
В метрологии — науке об округлениях и погрешностях, результат принято округлять до двух значащих цифр. Что же это значит? Значащая цифра — это цифра от первой, отличной от нуля.
Есть три случая, для которых есть свои особенности округления:
Когда мы имеем дело с числами меньше единицы, необходимо округлять результат до двух знаков после запятой. Например, число 0,7342. Округляем это число до 0,734, а потом до 0,73. Именно так и должен быть округлён результат. Первый ноль не является значащей цифрой.
Попробуем округлить 8,357. Первая цифра 8 является значащей, так как она отлична от нуля. Соответственно, нам необходимо округлить результат до одного знака после запятой. Согласно правилам, о которых мы говорили выше, результат будет равен 8,4.
Теперь самый сложный случай. Попробуем округлить 47,336. Так как все цифры отличны от нуля, мы будем округлять результат до целого числа. По математическим правилам он будет равен 47. Если мы имеем дело с трёхзначным числом, необходимо округлить результат до двух знаков, после чего умножить на 10 в нужной степени. Пример: округляем 4289,346 и получаем 43, умноженное на десять в квадрате.
Именно для того и нужна метрология, чтобы правильно округлять и записывать результат в технической документации. А также для избежания ошибок при ведении расчетов в разработке технических устройств.
Заключение
Теперь вы знаете, как правильно округлять и сможете делать все необходимые расчеты самостоятельно. Главное, доходы округлять в меньшую сторону, а расходы — в большую. И тогда вам точно будет хватать денег на все покупки, и останется небольшая сумма, которую можно потратить на развлечения. Успехов вам!
Видео
В нашем видео подробно рассказано о правилах округления чисел — с примерами.
Точка и запятая между цифрами
Целая часть от дробной в русском языке отделяется только запятой. Однако из этого не следует, что везде в русском тексте точка между цифрами должна быть заменена запятой: нужно сначала убедиться, что перед нами именно дробь.
Номера версий программных продуктов и ай-пи-адреса не являются дробями.
Картошка, лук, редиска и морковь стоят 3,85, 4,55, 2,99 и 5,67 рублей, соответственно. Пример немного надуманный, но демонстрирует, почему запятая как разделитель дроби — это плохо.
В общем, я использую точку, зоопарк стандартов разделения дробей не нужен. Это все равно, что использовать кириллицу в формулах.
«Картошка, лук, редиска и морковь стоят 3,85, 4,55, 2,99 и 5,67 рублей, соответственно» — это не «немного надуманный» пример, а совершенно неестественная фраза.
Обычный человек запишет: «Картошка стоит 3,85; лук — 4,55; редиска — 2,99; а морковь — 5,67»; или вовсе оформит это таблицей.
>.. ай-пи-адреса не являются дробями
а кто их посчитал дробями?
Никогда не понимал, почему в русском языке не используется десятичная точка. Ведь цифры — это алфавит математики, а точка, +, − и прочие символы — это ее пунктуация. А математика не делится на «русскую» и всю остальную. Поэтому я считаю использование так называемой десятичной запятой нонсенсом.
Русский язык — живой язык, и он постоянно приспосабливается под потребности говорящих и пишущих на нем. Надеюсь, пройдет не слишком много времени до того светлого момента, когда десятичная запятая умрет де юре, — ведь де факто она умерла в момент начала широкого распространения компьютеров, как бы производители разнообразного софта ни пытались доказать обратное.
Илья, а я пытался вставить дробь как символ, но всё равно вышел код 188.
То, что у меня не поддерживается и УТФ-8 — тоже не новость. Допишу Эгею — будет.
У меня уже ощущение, что люди специально экзотические символы пихают, лишь бы лишний раз напомнить мне, что у меня нет УТФ-8.
Илья, специально для тупых: я нажимаю на клавиатуре Ctrl+Alt+M, чтобы получить знак «минус». Где тут HTML?
Про UTF-8 уже прочитал, так что можете не отвечать.
Конечно читал. Без этой книжки разработчик профнепригоден 🙂
Вы совершенно правы, и проблема с УТФ-8 даже уже решена в моих внутренних билдах. Но там есть другие проблемы, которые пока не позволяют перейти мне тут на новьё.
Георгию Тудоси:
Вы очень сильно заблуждаетесь говоря о том, что математика стандартизированна. Например, в русской традиции принято обозначать количество сочетаний из n по k через большую букву «С», во всем же остальном мире принято обозначать сочетания так же как и матрицу 2×1 (и это оправданно, так как сочетания допускают огромное количество манипуляций со своими параметрами, в качестве которых порой выступают экстремально сложные выражения).
Рекомендую еще почитать современные французские учебники по математике — вы будете шокированы. У французов, например, число «ноль» одновременно и положительное и отрицательное, а перемножение матриц осуществляется совершенно не так как у нас (вместо умножения строк левой матрицы на столбцы правой, они умножают столбцы левой на строки правой). Это из невинного.
Или вот еще: у нас знак деления часто обозначают двоеточием. В любой западной литературе двоеточие между двумя числами может лишь показывать отношение между двумя величинами, но никак не деление (что тоже крайне разумно, так как дети с пеленок начинают манипулировать дробями — у нас же в школах приходится вводить дроби отдельно, что просто глупая трата времени).
Что касается точки как разделителя целой и дробной части, то мне по большому счету наплевать. Я все равно в основном пишу на английском [смайл, показывающий язык].
Да. Ибо традиции надо блюсти.
П
ри этом нельзя не признать, что «нерусская» традиция отделять десятичные точкой гораздо практичнее.
Георгий Тудоси, вы, вероятно, удивитесь, но десятичная запятая — не отличительный признак какой-нибудь особенной «русской» математики: она используется в большинстве стран. Десятичная точка используется только в англоговорящих странах и их бывших колониях, а также в государствах, тесно связанных с английским миром, например, в Японии и Южной Корее. Это характерная особенность именно английского языка, так что, уж простите, довольно глупо говорить о том, что использование десятичной запятой — нонсенс, и она «де-факто умерла».
СИ, тем не менее, разрешает использовать или запятую, или точку по выбору, но с оговоркой «The decimal marker chosen should be that which is customary in the context concerned». Любопытно, что в этом документе запрещается использование запятой или точки в качестве разделителя разрядов.
«Запрещается» — но не карается. И там вот ещё какой запрет:
(А сколько крови пролито за это. )
#4 Юрко 1 июня 2009, 20:49
> Картошка, лук, редиска и морковь стоят 3,85, 4,55, 2,99 и 5,67 рублей, соответственно.
. 5,67 рубля соответственно. (Пять и 67 сотых рубля; да и «соответственно» в конце не является вводным словом.)
От числа часто должен отделяться не только знак градуса, но и любое обозначение единицы измерения. Правило очень простое: если при написании величины словами пробел ставится, то он нужен и при написании цифрами. Поэтому, например, «концентрация раствора 15 %», но «15%-ный раствор».
Я только заострил «меч правды». Издательство такое дело, что чем больше однообразия (в обозначениях того же самого), тем легче всем работать.
Но обычный читатель (даже и не тупой) не часто любуется красотой значков — он черпает информацию.
Так вот: градус (?), как прочие единицы СИ, ДОЛЖЕН от цифр (указывающих число этих градусов) быть отделён — как и любое «номальное» слово. Но есть какие-то. психофизиологические, что ли. законы набора текста: вот даже умный Devgru пишет (или пускай даже берёт с солидного сайта):
Как любит говорить хозяин блога, «ау, пробел?»! Таков реал!
Для себя я обычно в тексте ставлю точку, а в таблицах запятую.
Прочитал заметку. Не понял, зачем она: это же очевидно.
Пошел в комментарии. Сильно удивился: сколько, оказывается, людей, для которых неочевидно именно первое, вводное предложение, хотя заметка-то, в общем, говорит не о том, что надо менять точку на запятую, а о том, когда этого делать не надо.
Жаль, нет возможности отвечать здесь, но конкретным людям. Илья, может быть, все-таки стоит подумать о древовидных комментариях? Люди часто хотят общаться друг с другом, а сейчас это не очень удобно. Про возможность отвечать людям по почте я знаю, если что. (Кстати, грош цена заявлению о том, что «адрес не будет опубликован», если все адреса комментаторов приходят подписавшемуся на дискуссию по почте.)
#19: Я невнятно выразился, извините. Я считаю математику универсальным языком, который должен быть стандартизован. Поскольку де-факто международным (научным) языком давно стал английский, думаю, логично привести математическую типографику (и вообще правила записи) именно к правилам, принятым в этом языке. Уверен, что преимущества от этого перевесят все трудности, связанные с процессом перехода. Хотя мне и странно писать «tan» вместо привычного «tg» (ау, знатоки, я правильно написал?), как-нибудь перестроюсь.
#22: Возможно, вы и правы, но точка используется в наиболее развитых (в отношении науки и техники) странах. Для меня это прямое указание на то, к чему следует стремиться.
#25: http://gramota.ru/biblio/public/32_8 — там вообще про пробелы много написано. И к этому сайту я привык обращаться во всех сложных случаях, когда не уверен в собственной правоте.
#31, 32, 33: А вот в продуктах Adobe можно ставить в качестве десятичного разделителя запятую. Она корректно обрабатывается. и немедленно заменяется (в полях для ввода чисел, не в тексте, конечно) на точку. Очень правильное поведение, по-моему. Набирай, как привык, а написано будет, как правильно.
>#12 Георгий Тудоси 1 июня 2009, 22:37
>Почему, кстати, символ «−» нормально не отображается?
>>Илья Бирман 1 июня 2009, 22:43
>>Потому, что в комментариях не поддерживается ХТМЛ, о чём написано для тупых.
Измените надпись с «ХТМЛ не работает» на «теги сосут». И со знаками разберитесь, ага☺.
Правильное округление чисел
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
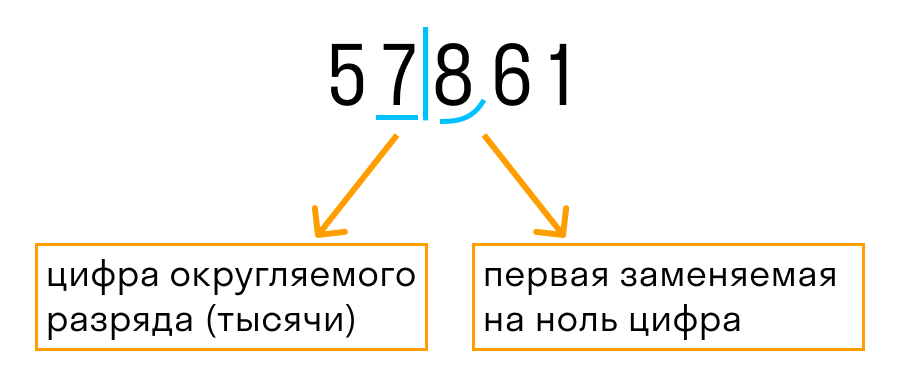
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
Разряды дробной части:
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
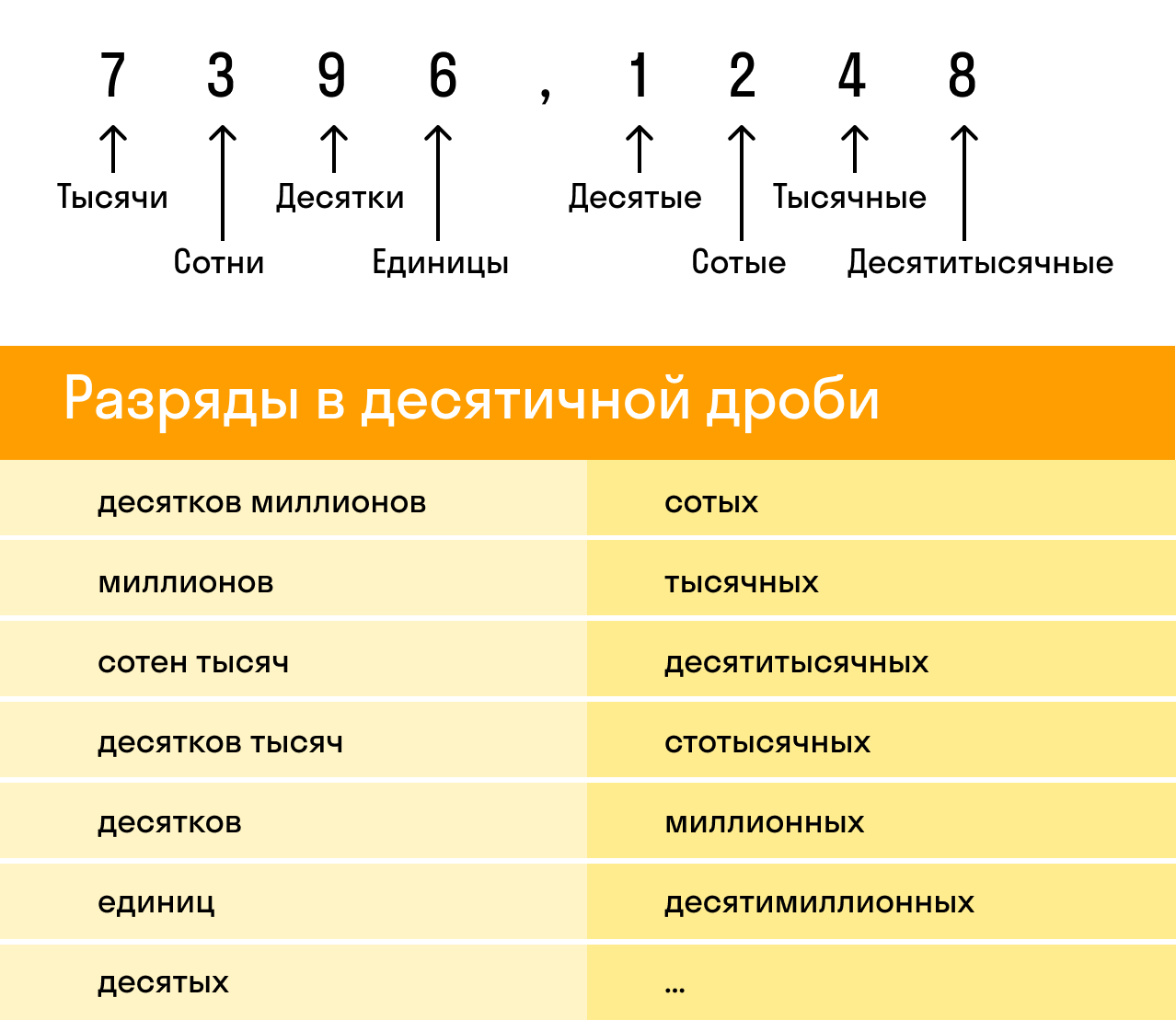
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.