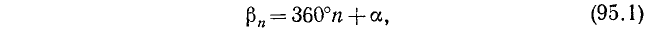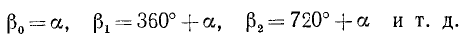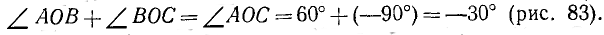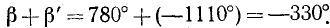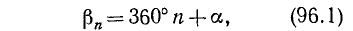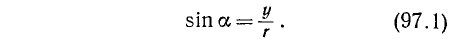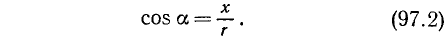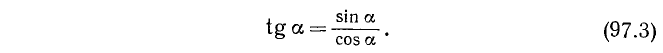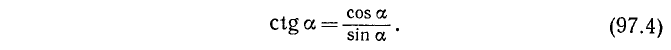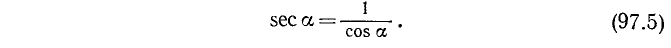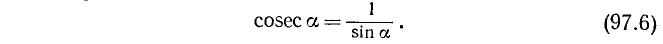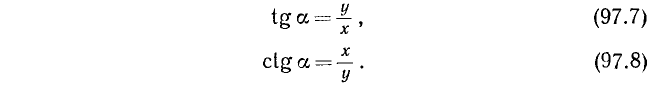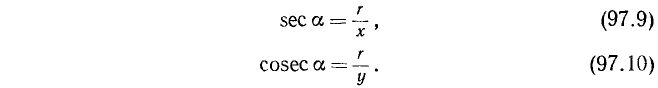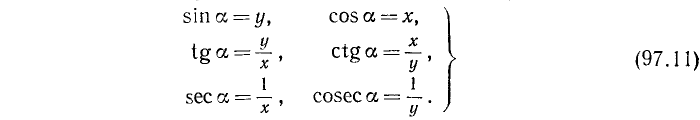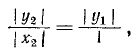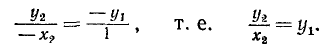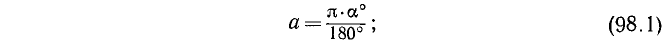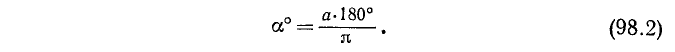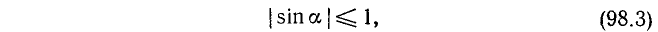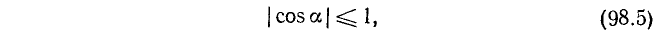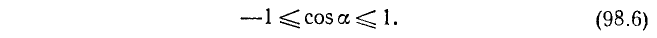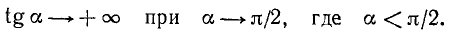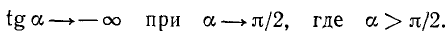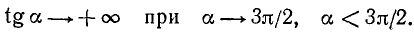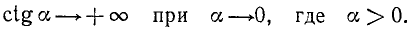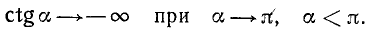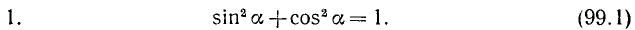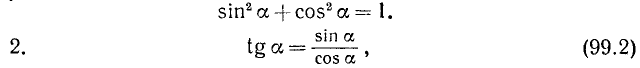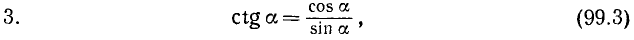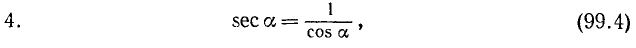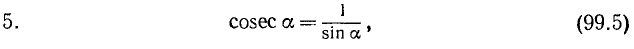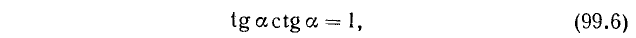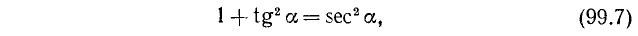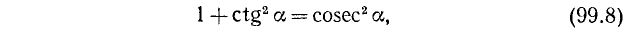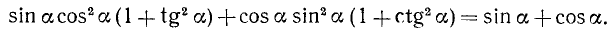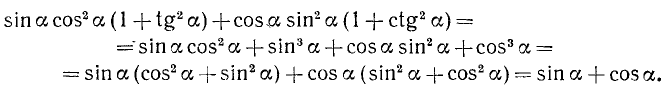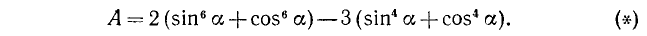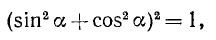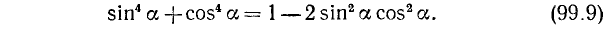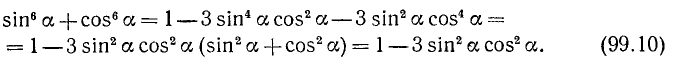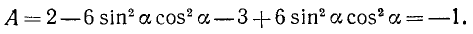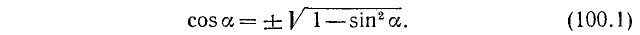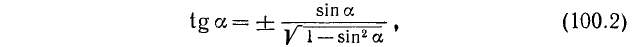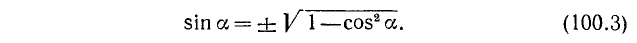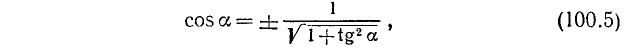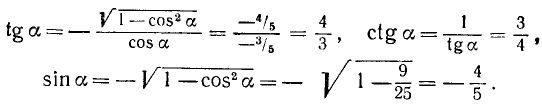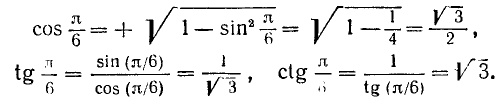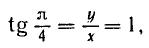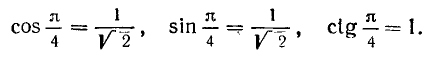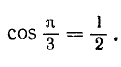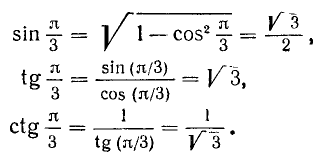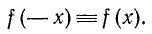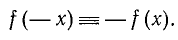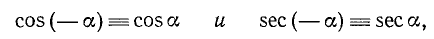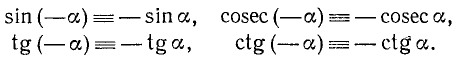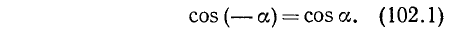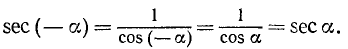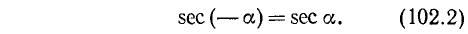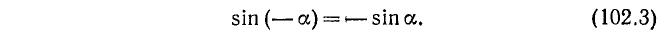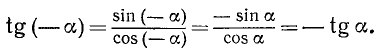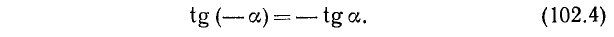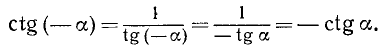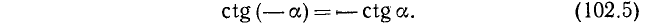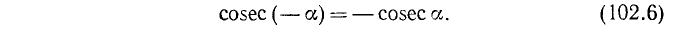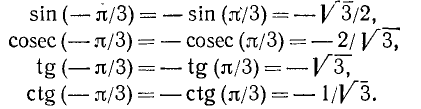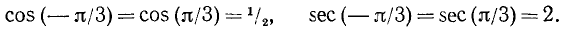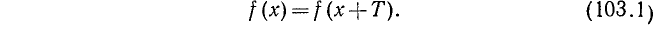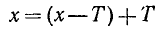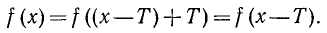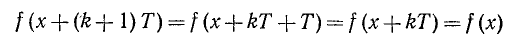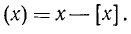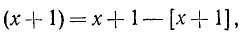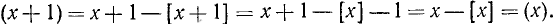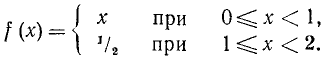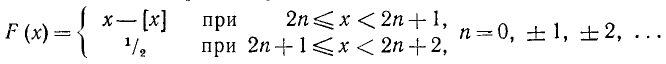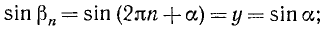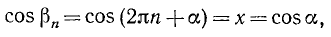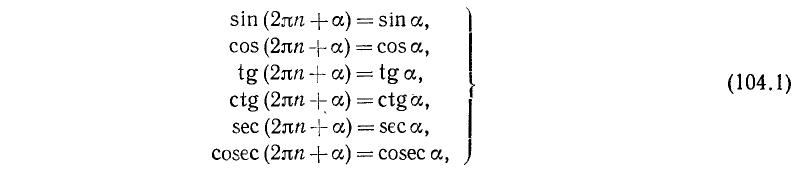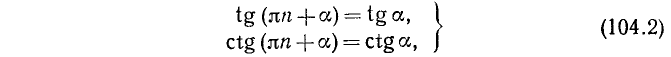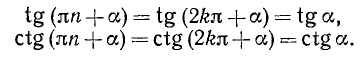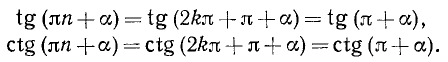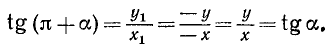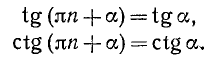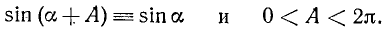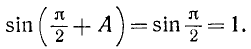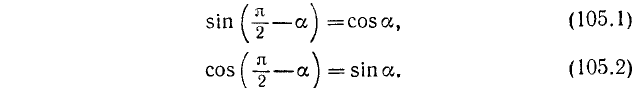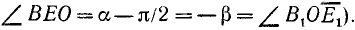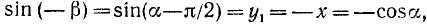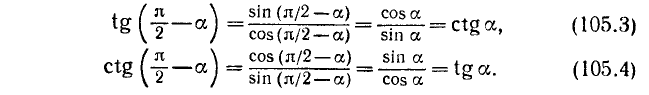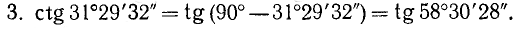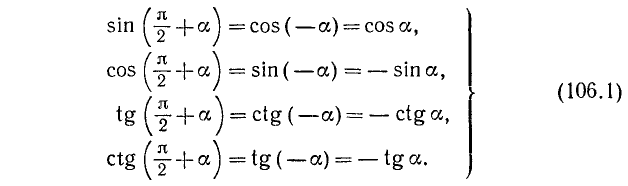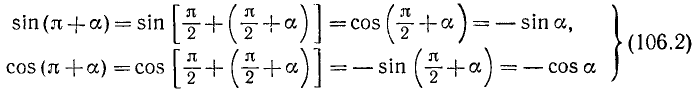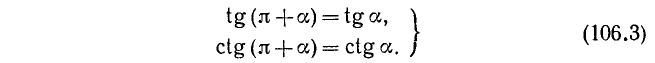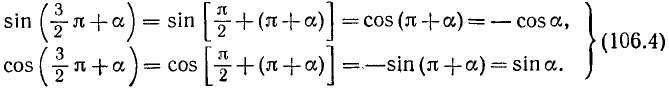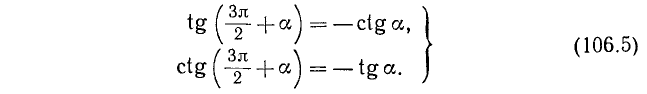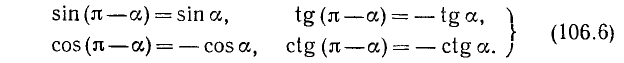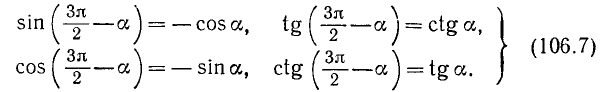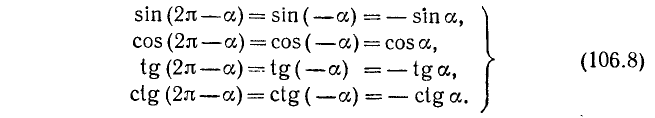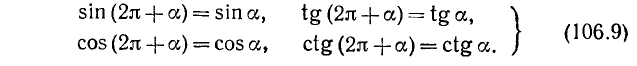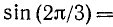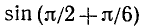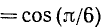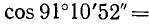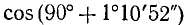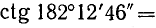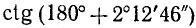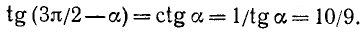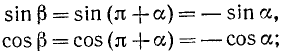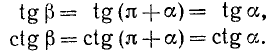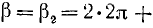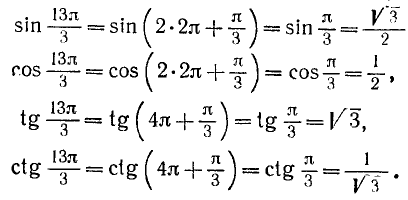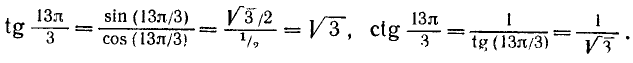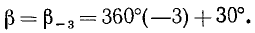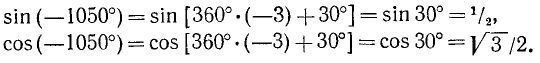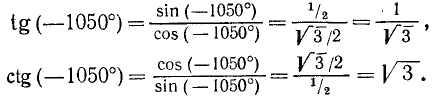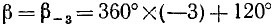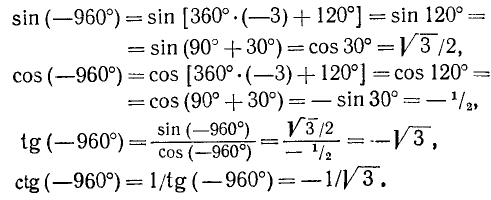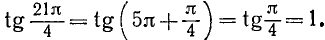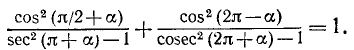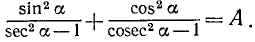Что означает значок дуги в математике в график
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Теорема 4:
Равные хорды стягивают равные дуги.
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Что означает знак дуги в геометрии – как обозначается дуга в геометрии
⌒ — Дуга (U+2312) — Таблица символов Юникода®
Начертание символа «Дуга» в разных шрифтах
Описание символа
Дуга. Разнообразные технические символы.
Связанные символы
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 8C 92 | 226 140 146 | 14847122 | 11100010 10001100 10010010 |
| UTF-16BE | 23 12 | 35 18 | 8978 | 00100011 00010010 |
| UTF-16LE | 12 23 | 18 35 | 4643 | 00010010 00100011 |
| UTF-32BE | 00 00 23 12 | 0 0 35 18 | 8978 | 00000000 00000000 00100011 00010010 |
| UTF-32LE | 12 23 00 00 | 18 35 0 0 | 304283648 | 00010010 00100011 00000000 00000000 |
Дуга (геометрия) — это… Что такое Дуга (геометрия)?
Дуга — связное подмножество окружности.
Свойства
*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha
Wikimedia Foundation. 2010.
Смотреть что такое «Дуга (геометрия)» в других словарях:
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
Геометрия — (γήμετρώ земля, μετρώ мерю). Понятия о пространстве, положении и форме принадлежат к числу первоначальных, с которыми человек был знаком уже в глубокой древности. Первые шаги в Г. были сделаны египтянами и халдеями. В Греции Г. была введена… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
АФФИННАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, изучающий дифференциально геометрич. свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства. В эквиаффинной … Математическая энциклопедия
РИМАНОВА ГЕОМЕТРИЯ — теория риманова пространства. Р и м а н о в ы м п р о с т р а н с т в о м наз. n мерное связное дифференцируемое многообразие М п, на к ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2 … Математическая энциклопедия
Сферическая геометрия — математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — математич. дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия
ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — геодезиче ская, геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный … Математическая энциклопедия
Декарт Рене — (Descartes) (латинизир. Картезий; Cartesius) (1596 1650), французский философ, математик, физик и физиолог. С 1629 в Нидерландах. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввёл многие алгебраические… … Энциклопедический словарь
Жорданова кривая — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
Дуга окружности. Полуокружность определение. Длина дуги окружности. Угол и дуга окружности
Дуга окружности
Что такое дуга окружности?
Дугу окружности принято обозначать тремя точками: две точки – это концы дуги и одна произвольная промежуточная точка. Пример дуги:
На картинке представлены две дуги: ACB и ADB.
Полуокружность определение
Полуокружностью называют дугу окружности, если отрезок, соединяющий её концы, в нашем случае AB, есть диаметр окружности.
На картинке ACB – полуокружность:
Градусная мера дуги окружности
Рассмотрим три случая.
Первый случай
Градусной мерой дуги ACB является градусная мера центрального угла AOB:
Второй случай
Третий случай
А чему равна сумма градусных мер дуг ADB и ACB?
Градусная мера дуги ADB равна 90 0 по условию.
Тригонометрические функции угла (дуги) в математике с примерами решения и образцами выполнения
Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Векторы. Обобщение понятий угла и дуги. Проекция вектора
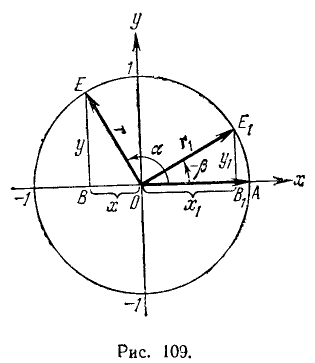
Вектором называется направленный отрезок в плоскости (в пространстве). При изучении тригонометрических функций мы будем рассматривать векторы в плоскости. С каждым вектором связывают понятия направления и длины (абсолютной величины, модуля).
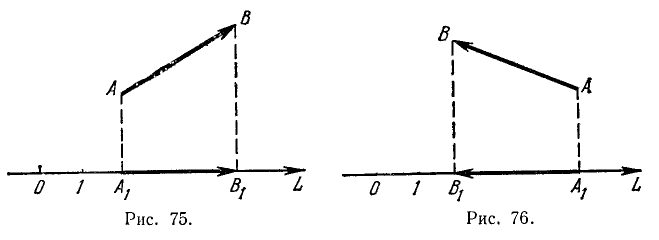
Для вектора (рис. 73) применяются следующие обозначения: 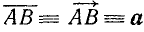
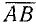
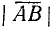
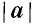
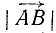
Для общности рассматривается и случай нулевого отрезка АА, начало которого совпадает с его концом. Такой отрезок называется нулевым вектором и обозначается через 0. Нулевой вектор имеет длину, равную нулю; ему не приписывается никакого направления.
Следует заметить, что всегда 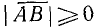
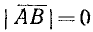
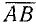
Для векторов не имеют смысла понятия «больше» или «меньше». Можно только говорить, что длина вектора 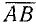
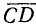
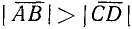
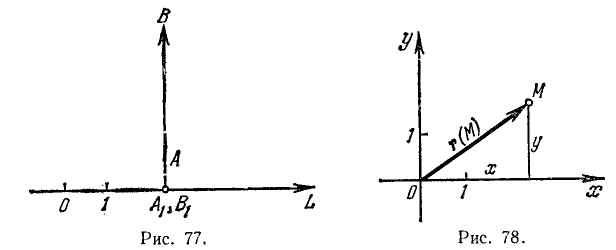
Два Еектора а и b называются равными, если они:
1) параллельны одной и той же прямой,
2) одинаково направлены,
3) имеют равные длины, т. е. |a| = |b| (рис. 74).
Совокупность векторов с указанным выше определением равенства обычно называют системой свободных векторов. Термин «свободный вектор» связан с тем, что теперь один и тот же вектор может быть изображен направленным отрезком с началом в любой точке: его можно свободно переносить из точки в точку.
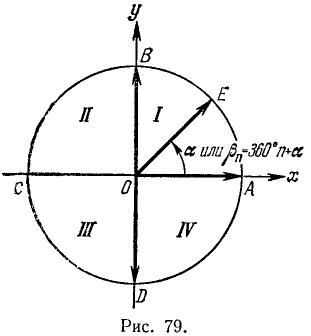
Каждому вектору 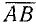
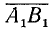
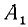
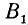
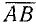
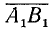
взятая со знаком плюс, если направление вектора 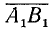
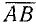
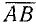
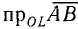
случаи: a) 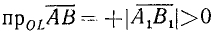
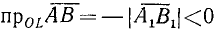
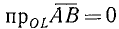
Рассмотрим теперь совокупность векторов, исходящих из одной точки (начала). Такая совокупность векторов называется центрированной. Примем эту общую точку за начало О декартовой прямоугольной системы координат Оху (см. п. 8).
Определение:
Положительные углы и дуги, меньшие 360°
На координатной плоскости Оху рассмотрим окружность радиуса R с центром в начале координат (рис. 79).
Будем считать, что угол 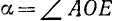
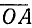
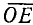
При вращении (в направлении против движения часовой стрелки) подвижный радиус-вектор описывает углы от 0° до З60° (определение градуса см. в п. 165). Осями координат круг на рис. 79 делится на четыре четверти: первая четверть АОВ, вторая BОС, третья COD и четвертая DOА. Если сторона ОЕ угла АОЕ расположена в первой, второй, третьей или четвертой четверти, то угол АОЕ будем называть соответственно углом первой, второй, третьей или четвертой четверти. В первой четверти угол 
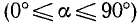
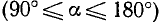
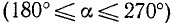
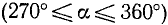
Если подвижный радиус-вектор описал угол АОЕ, равный 
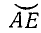

Углы и дуги, большие 360°
Мы ограничивались углами от 0° до 360°. Между тем в различных задачах приходится иметь дело с вращениями, при которых совершается больше полного оборота, например с вращением маховика, с полетом спутника вокруг Земли и т. д. Эти задачи приводят к необходимости обобщения понятия угла (дуги), к необходимости введения углов (дуг), больших 360°. Рассмотрим угол 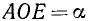
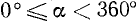
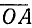
где 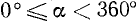
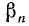



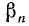
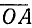
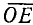
Если подвижный радиус-вектор описал угол 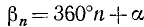
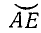
Отрицательные углы. Сложение и вычитание углов
Назовем вращение подвижного радиуса-вектора в направлении против движения часовой стрелки положительным, а в противоположном направлении (в направлении по движению часовой стрелки) — отрицательным. Угол, описанный при отрицательном вращении подвижного радиуса-вектора, назовем отрицательным углом.
Правило. Угол измеряется положительным числом, если он положительный, и отрицательным числом, если он отрицательный.
Пример:
На рис. 80 изображены два угла с общей начальной стороной 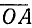
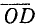
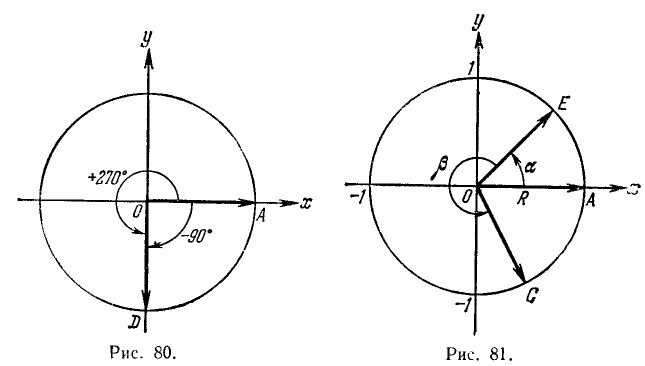
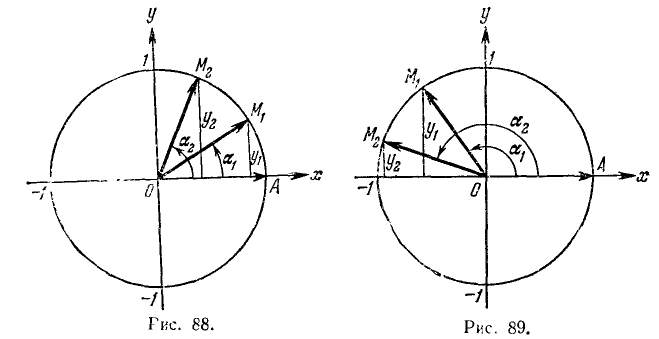
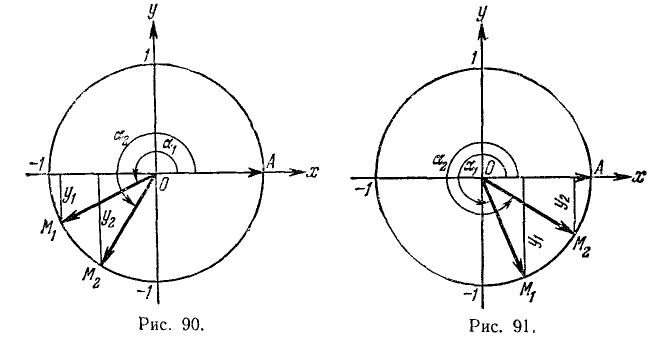
Сумма двух углов. Па координатной плоскости Оху рассмотрим окружность единичного радиуса с центром в начале координат (рис. 81). Пусть произвольный угол 
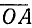
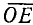
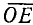
(на чертеже положительный), который получим в результате вращения некоторого подвижного радиуса-вектора от его начального положения 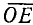
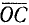

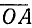
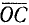
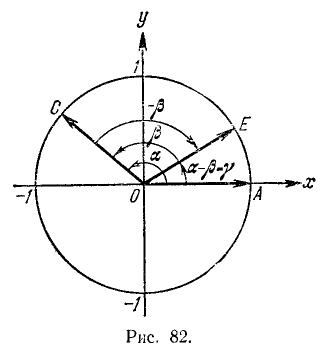
Разность двух углов. Под разностью двух углов 
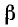

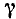
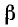

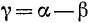
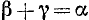

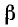

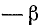
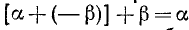
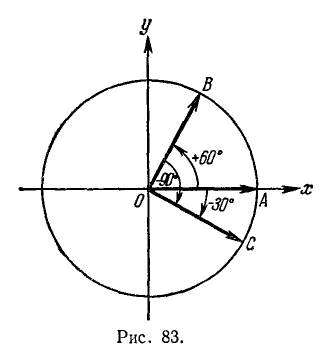
Пример:
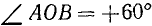
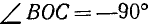
Пример:
Угол 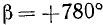
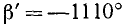
В формуле (95.1) предполагалось, что n — любое целое неотрицательное число. Если же предположить, что n —любое целое число (положительное, отрицательное или нуль), то при помощи формулы
где 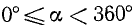
Пример:
Угол, равный —1370°, можно записать так:
—1370° = 360° (—4)+ 70°.
Здесь n = —4, 
Заметим, что все углы 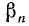
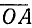
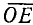

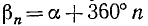
Тригонометрические функции произвольного угла
Определение основных тригонометрических функций: Было дано общее определение функциональной зависимости (общее определение функции) и изучались некоторые элементарные функции. Теперь мы введем основные тригонометрические функции.
Пусть радиус-вектор 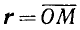


2. Косинусом угла 
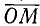
Ниже (замечание 1) мы покажем, что sin а и cos а, определенные равенствами (97.1) и (97.2), действительно зависят лишь от угла а (но не от радиуса окружности r).
3. Тангенсом угла а (обозначение: tg a) называется отношение синуса угла а к косинусу этого угла:
4. Котангенсом угла а (обозначение: ctg a) называется отношение косинуса угла а к синусу этого угла:
5. Секансом угла a (обозначение: sec а) называется величина, обратная cos а:
6. Косекансом угла а (обозначение: cosec a) называется величина, обратная sin а:
Замечание:
Тригонометрические функции (97.1) — (97.6) действительно являются функциями только угла а, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор r образует с осью абсцисс данный угол а, то отношения х/r и у/r не зависят от длины радиуса-вектора; читатель легко в этом убедится.
Замечание:
Из определения tg a и ctg a следует, что
Соотношения (97.7) и (97.8) можно было бы принять в качестве определений для tg a и ctg a.
Замечание:
Соотношения (97.9) и (97.10) можно было качестве определений для sec а и cosec a.
Замечание 4. Во всех определениях (97.1) — (97.6) мы предполагаем, что соответствующие отношения существуют (имеют смысл). Например, tg a имеет смысл, если 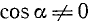
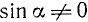
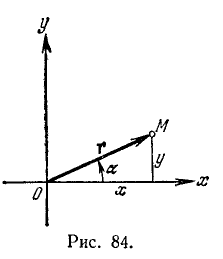
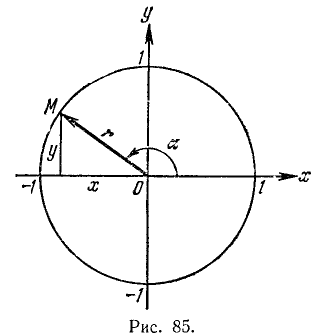
В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис. 85):
Формулы для tg a и ctg a остались прежними (см. (97,7) и (97.8)), а формулы для остальных основных тригонометрических функций приняли более простой вид (см. (97.1), (97.2), (97.9) и (97.10)). Следовательно, синус и косинус угла а равны соответственно ординате и абсциссе конца подвижного единичного радиуса-вектора.
Конец этого единичного радиуса-вектора при изменении угла а от 0° до 360° опишет окружность, называемую единичной окружностью (рис. 85). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов.
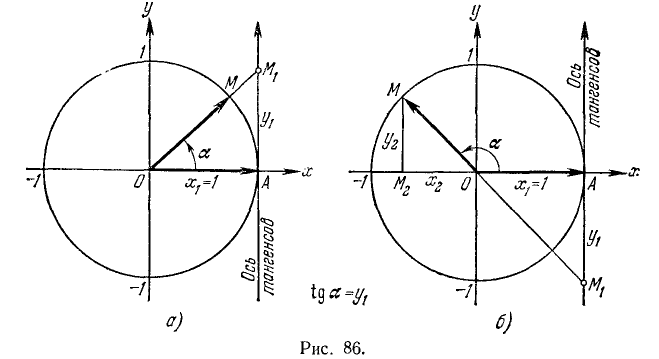
Осью тангенсов называется перпендикуляр, восставленный в точке А к неподвижному радиусу-вектору 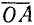
Рассмотрим угол 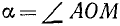
а) Если точка М единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку 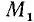
б) Если точка М единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку 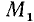
Заметим, что тангенс угла а численно равен ординате 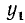
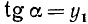
1) 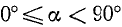
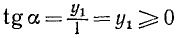
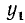
2) 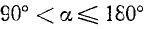
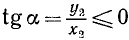
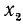
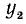
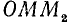
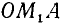
Следовательно, 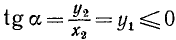
Заметим еще следующее:
а) если точка М лежит на оси ординат (например, а = 270°), то соответствующей ей точки оси тангенсов не существует, но при этом и tg a также не существует;
б) в рассмотренных случаях 1) — 4) мы брали угол а в пределах от 0° до 360°, но в наших рассуждениях ничего не изменится, если мы будем предполагать угол а любым.
Осью котангенсов называется перпендикуляр, восставленный в точке В (конец радиуса-вектора 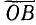
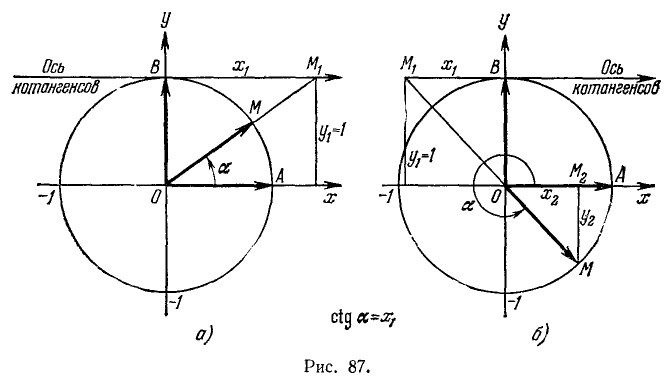
Положительное и отрицательное направления на оси котангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси абсцисс (рис. 87). Введем понятие соответствующей точки оси котангенсов.
а) Если точка М единичной окружности лежит над осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку 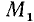
б) Если точка М единичной окружности лежит под осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку 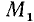
Аналогично предыдущему можно получить, что котангенс угла а равен абсциссе х, соответствующей точки оси котангенсов, т.е. 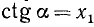
Изменение основных тригонометрических функций при изменении угла от 0 до 2 пи
Изменение основных тригонометрических функций при изменении угла от 0 до 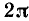
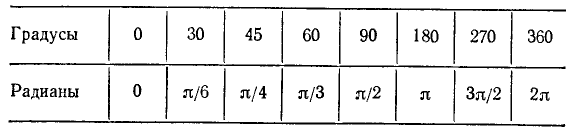
В дальнейшем мы будем использовать не только градусную, но и радианную меру углов (см. п. 166); радианное измерение углов станет особенно важным при переходе к тригонометрическим функциям числового аргумента (п. 107). В связи с этим напомним некоторые факты из геометрии, относящиеся к градусной и радианной системам измерения углов и дуг:
1) при измерении углов и дуг в радианной системе наименование единицы измерения — радиана обычно опускают и говорят, например, «угол равен 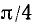
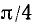
2) при переходе от градусной меры (а градусов) к радианной мере (а радиан) пользуются формулой
3) при переходе от радианной меры (а радиан) к градусной мере (а градусов) пользуются формулой
Полезно запомнить соответствующие значения в градусной и радианной мере некоторых наиболее часто встречающихся углов, приведенные в следующей таблице.
Рассмотрим теперь, как изменяется (по абсолютной величине и знаку) каждая из основных тригонометрических функций при изменении угла а от 0 до 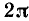
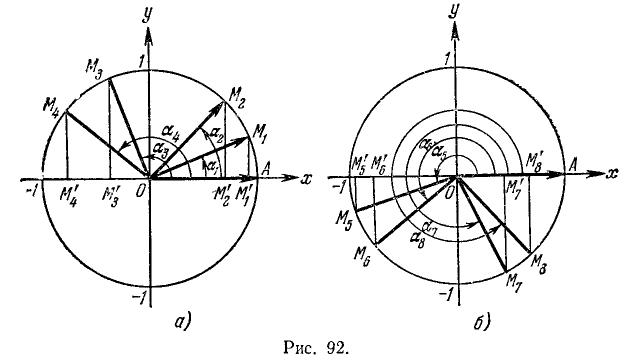
I. sin а. Согласно первой формуле (97.11) sin a = у, где у — ордината конца подвижного единичного радиуса-вектора (см. рис. 85).
1) 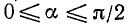
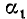
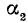
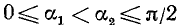
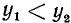
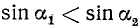
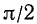
2) 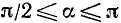
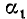
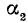
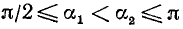
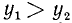
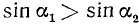
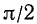
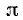
3) 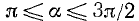
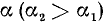
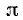
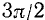
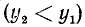
4) 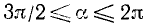
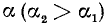
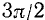
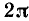

Вывод. При любом угле а абсолютная величина sin а не превосходит 1, что записывается так:
или в равносильной форме:
II. cos а. По второй формуле (97.11) cos a = x, где х — абсцисса конца подвижного единичного радиуса-вектора (рис. 85).
1) 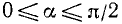
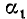
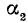
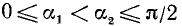
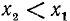
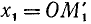
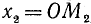
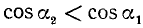
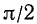
2) 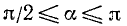
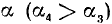
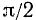
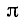
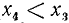
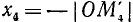
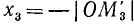
3) 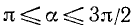
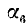
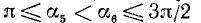
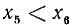
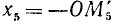
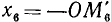
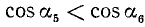
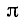
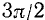
4) 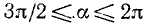
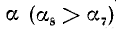
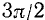
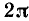
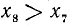
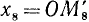
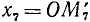
Вывод. При любом угле а абсолютная величина cos а не превосходит 1, что записывается так:
или в равносильной форме:
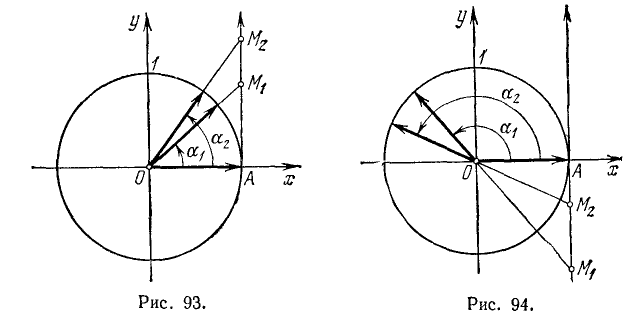
III. tg a. Тангенс угла а численно равен ординате соответствующей точки оси тангенсов (см. п. 97).
1) 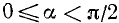
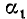
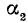
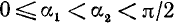
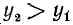
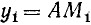
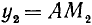
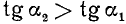
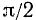
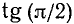
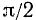
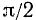
Сходное положение встречалось при изучении функции у = 1/х; если х приближается к нулю, оставаясь больше нуля, то у = 1/х стремится к плюс бесконечности.
Это же условно записывают так:
2) 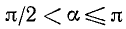
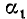
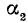
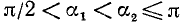
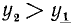
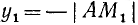
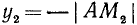

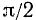
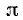
Если а стремится к 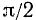
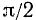
3) 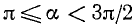
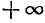
Если а стремится к 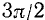
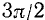
4) 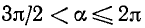
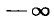
Если а стремится к 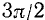
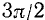
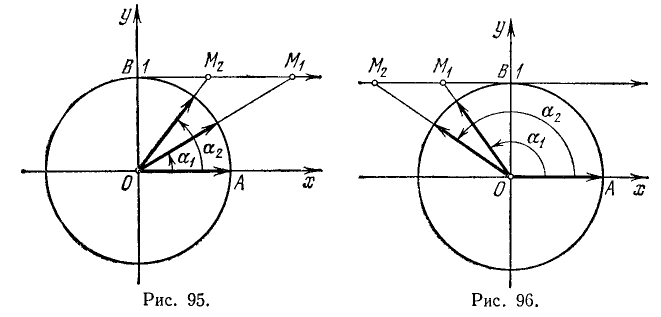
IV. ctg a. Котангенс угла а численно равен абсциссе соответствующей точки оси котангенсов (см. п. 97).
1) 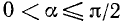
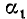
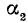
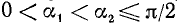

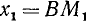
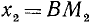
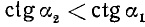
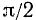
2) 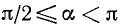
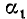
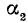
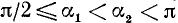
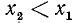
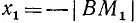
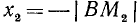
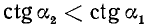
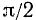
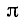
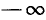
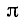
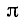
Разбор поведения ctg a в остальных четвертях предоставляется читателю. Приведем только окончательные результаты:
3) 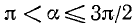
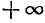
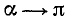
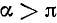
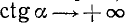
4) 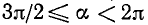
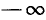
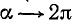
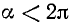
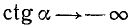
Соотношения между тригонометрическими функциями одного и того же угла
Основные тригонометрические тождества: Между основными тригонометрическими функциями произвольного угла а имеются следующие тождественные соотношения:
Доказательство. Принимая |r| = r = 1, получим (для произвольного угла a) sin а = у, cos a = x, где х и y — проекции единичного радиуса-вектора на оси координат (см. рис. 85). По теореме Пифагора (см. п. 216) 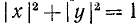
Тождества (99.2) и (99.3) служат соответственно определениями функций tg a и ctg a (см. формулы (97.3) и (97.4)).
Тождества (99.4) и (99.5) служат соответственно определениями функций sec а и cosec а (см. формулы (97.5) и (97.6)).
Тождества (99.1)—(99.5) назовем основными. При помощи этих основных тождеств выведем так называемые дополнительные тождества.
6. Перемножив почленно тождества (99.2) и (99.3), получим
7. Разделив тождество (99.1) почленно на 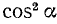
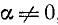
8. Разделив тождество (99.1) почленно на 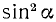
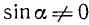
При помощи тождеств (99.1)—(99.8) можно производить преобразования различных выражений, содержащих тригонометрические функции, и получать новые тождества. Пример 1. Доказать тождество
Решение:
Заменив в левой части tg a и ctg a их выражениями по формулам (99.2) и (99.3), получим
После выполнения тождественных преобразований левая часть равенства совпала с правой. Исходное тождество этим доказано.
Это же тождество можно доказать и по-другому, воспользовавшись формулами (99.7) и (99.8), а затем формулами (99.4) и (99.5). Рекомендуем это сделать читателю.
Пример:
Решение:
Используя тождество (99.1), получаем
Подставив (99.9) и (99.10) в (*), будем иметь
Вычисление значений тригонометрических функций по значению одной из них
При помощи формул (99.1)—(99.8) можно выразить (с точностью до знака) через любую из шести тригонометрических функций угла а остальные пять функций. Мы ограничимся только функциями sin a, cos а и tg a.
Подставив найденное значение cos а в тождество (99.2), получим
где 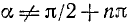
2. Выражение через cos а. Из тождества (99.1) находим
Подставив найденное значение sin а в тождество (99.2), получим
где 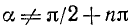
3. Выражение через tg a. Из тождества (99.7) находим 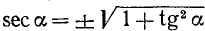
где 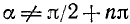
где 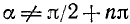
При извлечении квадратного корня знак следует выбирать в зависимости от того, в какой четверти находится угол а.
Пример:
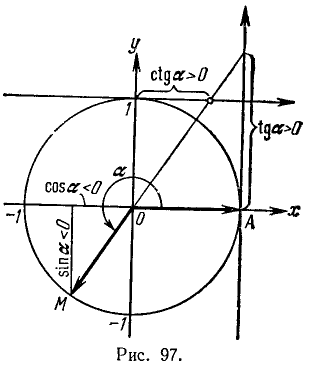
Известно, что cos a = —3/5 и 180° 0, ctg a > 0, sin a
В дальнейшем мы будем использовать следующий факт:
Для того чтобы два действительных числа х и у можно было принять за cos а и sin а одного и того же угла а, необходимо и достаточно, чтобы сумма их квадратов была равна единице: 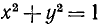
Доказательство:
Необходимость. Если х = cos а и у = sin а, то по тождеству (99.1) 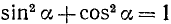
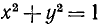
Достаточность. Рассмотрим радиус-вектор 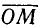
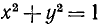
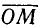
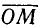
Пример:
Могут ли sin а и cos а одного и того же угла a быть равными соответственно: а) 12/13 и —5/13; б) 1/3 и —2/3?
Решение:
а) Числа 12/13 и —5/13 обладают тем свойством, что 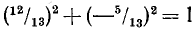
б) Для чисел 1/3 и —2/3 имеем 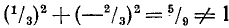
Значения тригонометрических функций некоторых углов
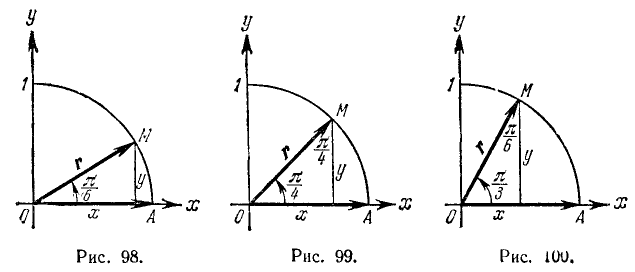
Воспользовавшись сведениями из геометрии, найдем значения тригонометрических функций углов 30°, 45° и 60° (или соответственно в радианной мере углов 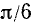
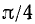
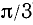
1) 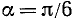
(поскольку r = 1). Воспользовавшись теперь формулами (100.1), (99.2) и (99.6), легко вычислим:
2) 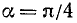
ибо у = х. Воспользовавшись теперь формулами (100.5), (100.6) и (99.6), легко найдем:
3) 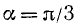
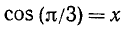
Далее воспользуемся формулами (100.3), (99.2) и (99.6):
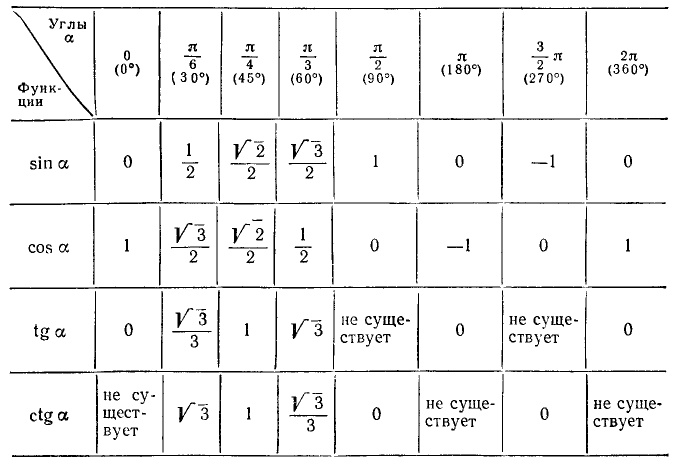
Присоединяя к полученным результатам результаты п. 98, составим следующую таблицу значений тригонометрических функций некоторых часто встречающихся углов.
О поведении tga a окрестности 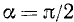
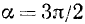
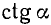
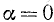
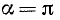
Четность, нечетность и периодичность тригонометрических функций
Четность и нечетность: Напомним (см. п. 33), что функция y = f(x) называется четной, если для всех допустимых значений аргумента х имеет место тождество
Функция y = f(x) называется нечетной, если для всех допустимых значений аргумента x имеет место тождество
Для тригонометрических функций справедлива следующая
Теорема:
Функции cos а и sec а являются четными, т.е.
а функции sin а, tg a, ctg a и cosec а являются нечетными, т. е.
Доказательство:
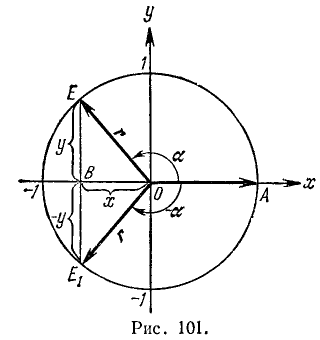
Рассмотрим два угла, образованных единичным радиусом-вектором r: 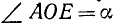
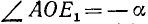
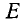
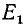
Согласно второй формуле (97.11) имеем cos a = x и cos (—а) = х, следовательно,
Так как равенство (102.1) справедливо для любого угла а, то мы доказали, что cos (— a) = cos a.
Четность sec a (см. формулу (99.4)) доказывается так:
Заметим, далее, что ординаты точек 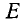
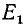
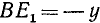
Используя формулу (99.2), а также тождества (102.1) и (102.3), получим
Для доказательства нечетности ctg a воспользуемся тождествами (99.6) и (102.4):
Рекомендуем читателю доказать, что справедливо и тождество
Пример:
Найти значения тригонометрических функций угла 
Решение:
Используя нечетность функций sin a, cosec а, tg a и ctg a, получим
Используя четность функций cos а и sec а, получим
Понятие периодической функции
Тригонометрические функции обладают свойством периодичности, которое определяется в общей форме следующим образом.
Определение. Функция f (х) называется периодической с периодом 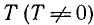
Число Т называется в этом случае периодом функции f(x). Докажем следующее предложение:
Если Т — период функции f(x), mo и любое из чисел nТ, п = —1, ±2, … , также является периодом f(x).
Доказательство:
Прозедем сначала доказательство для —Т. Для этого рассмотрим пару значений аргумента х и х+(—Т)=х—Т. Из записи
видно (в силу определения периодичности), что если функция определена в одной из точек х—Т, х, то она определена и во второй точке. Далее устанавливаем равенство f/(х—T) = f(x):
Доказательство того, что nТ при натуральном n является периодом функции f(x), проведем по индукции (случай отрицательного n сводится к этому заменой Т на —Т). Итак, требуется установить, что если f(х) определена в одной из точек x, х + nТ,
то она определена и во второй точке, причем f (x) = f (х + nТ). Допустим, что утверждение теоремы уже доказано для некоторого n = k (оно, например, очевидно при n = 1). Докажем, что оно останется верным и для n = k + 1. Прежде всего, в силу того, что Т — период, замечаем, что если одно из значений аргумента x + kT и x + (k + l)T = (x + kT) + T принадлежит области определения функции, то ей принадлежит и второе значение. Так как, по предположению индукции, такое же положение справедливо и для пары точек х и x + kT, то видно, что точки х и х + (k + 1)T принадлежат (или не принадлежат) области определения f(х) одновременно. Далее устанавливаем равенство значений f(x) в точках x и x + (k + 1)T:
(последнее — по предположению индукции).
Доказано, что nТ — период функции при любом целом n. Наименьший положительный период функции (если он существует) называется основным периодом.
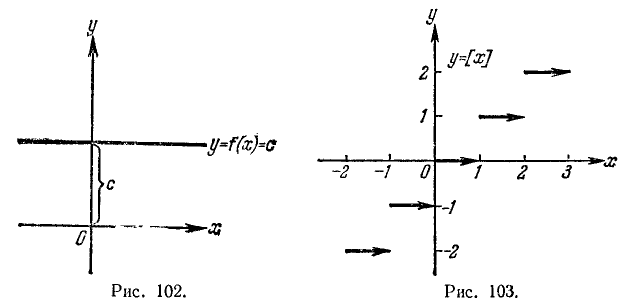
Пример:
Функция f(х) = с (с — постоянная величинa) имеет своим периодом любое число. Основного периода здесь нет. График этой функции изображен на рис. 102.
Пример:
Напомним, что целой частью числа х (обозначение: [x]) называется наибольшее целое число, не превосходящее х (п. 4). Целая часть х есть функция от х; ее график показан на рис. 103.
Дробной частью числа х (обозначение: (x)) мы назвали (п. 4) разность между х и его целой частью:
Дробная часть х является периодической функцией с основным периодом T = 1. Действительно,
и так как очевидно, что [x + 1] = [х] + 1,то
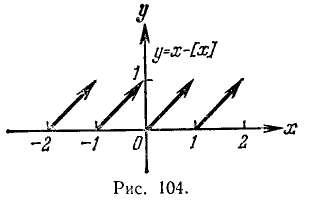
График дробной части х показан на рис. 104.
Пример:
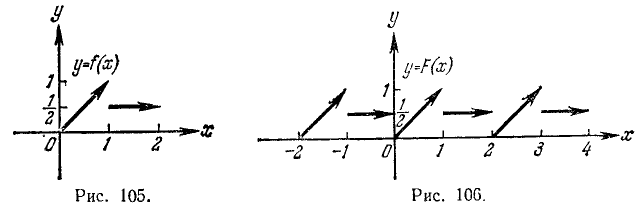
а) Рассмотрим следующую функцию f(х), определенную для х, удовлетворяющих неравенствам 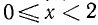
График функции изображен на рис. 105.
б) С помощью этой функции f(x), приняв за основной период число T = 2, построим периодическую функцию F (х):
График функции F (х) изображен на рис. 106.
Периодичность тригонометрических функций
Одним из важных свойств тригонометрических функций является свойство периодичности, с которым мы в общем виде познакомились в п. 103. Докажем следующую теорему о периодичности тригонометрических функций.
Теорема:
Тригонометрические функции sin a, cos а, tg a, ctg a, sec а и cosec а являются периодическими функциями, причем основной период функций sin a, cos a, sec а и cosec а равен 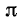
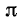
Пока мы рассматриваем тригонометрические функции угла, и период Т следует рассматривать как угол; это замечание сохраняет силу вплоть до п. 107, где вводятся тригонометрические функции числового аргумента.
Доказательство:
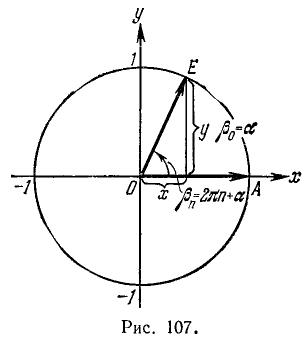
В пп. 95 и 96 мы ввели углы вида 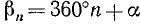
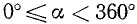
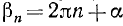
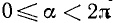
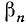
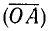
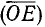
если воспользоваться второй из формул (97.11) для определения косинуса, то получим
так как соответствующие значения х и у для угла а и углов 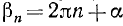
Аналогичный результат получается и для других тригонометрических функций. Мы приходим к следующим формулам:
где n = 0, ±1, ±2, …
Этим уже доказано, что 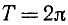
Рассмотрим два случая.
а) n = 2k, т. е. n — четное число (k = 0, ± 1, ±2, …). В этом случае имеем
Здесь мы использовали полученные ранее формулы (104.1),
б) n = 2k + 1, т. е. n—нечетное число (k = 0, ±1, ±2, …). В этом случае имеем
Здесь мы использовали формулы (104.1).
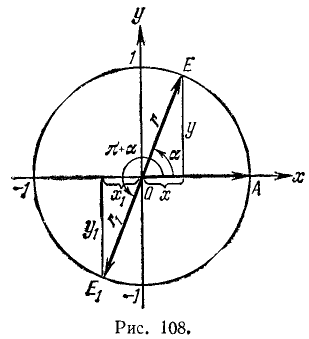
Из геометрических соображений (рис. 108) следует, что 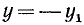
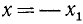
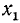
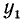
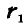
Аналогично получаем 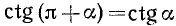
Для углов в градусной мере аналогичные формулы получим, заменив в формулах (104.1) 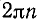
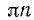
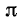
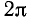
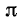
Доказательство:
Требуется показать, что 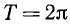
Так как в последнем равенстве а может быть любым (ведь это равенство, по предположению, выполняется тождественно), то должно выполняться, например, равенство
Для sin а наше утверждение доказано. Аналогично оно доказывается и для других тригонометрических функций.
Зависимость между тригонометрическими функциями дополнительных углов
Углы 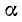
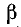
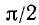
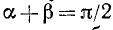
Теорема:
Сходные тригонометрические функции дополнительных углов равны между собой.
Доказательство:
Докажем сначала, что
Предположим для определенности, что 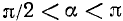
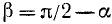
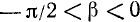
Построим теперь с помощью подвижного единичного радиуса-вектора r углы 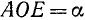
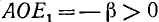
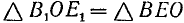
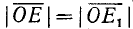
Из равенства треугольников имеем 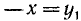
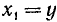
откуда 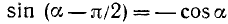
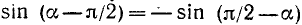
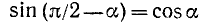
Аналогично доказывается, что 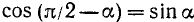
Для остальных функций можно доказательство вети так:
При выводе формул (105.3) и (105.4) мы пользовались только что доказанными формулами (105.1) и (105.2).
Замечание:
При доказательстве теоремы мы считали, что угол а задан в радианах. Соответствующие формулы для угла а, измеренного в градусной мере, легко получить из формул (105.1) —(105.4), заменив 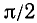
Замечание:
При доказательстве теоремы мы предположили для определенности, что угол а удовлетворяет неравенствам 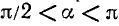
Пример:
Заменить данные тригонометрические функции тригонометрическими функциями дополнительного угла:
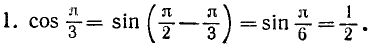
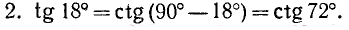
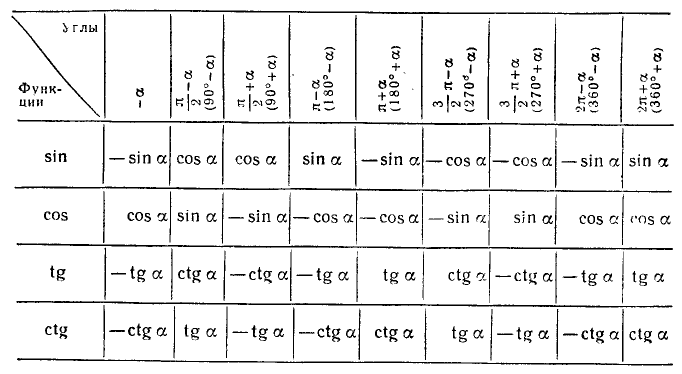
Формулы приведения
Формулами приведения называются формулы, выражающие тригонометрические функции углов 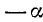
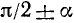
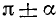
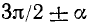
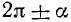
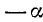
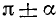
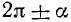
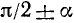
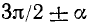
Пользуясь возможностью произвольного выбора угла а в формулах (105.1) — (105.4), получим новые важные формулы (мы ограничимся функциями sin a, cos a, tg a и ctg a).
а) Заменив в формулах (105.1)—(105.4) а на —а, получим
б) Заменив в формулах (106.1) a на 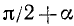
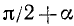
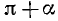
(мы снова воспользовались тем, что формулы (106.1) справедливы для произвольного угла а). Так как 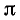
в) Аналогично получим
Рекомендуем читателю доказать, что
г) Заменив в формулах (106.2) и (106.3) а на —а, получим
д) Заменив в формулах (106.4) и (106.5) а на —а, получим
е) В силу того, что 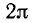
ж) Аналогично е), будем иметь
Рекомендуем читателю написать формулы, аналогичные формулам (106.1)—(106.8), для углов в градусной мере, заменив в последних 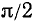
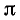
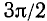
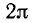
Пример:
Пользуясь формулами приведения, найти значения следующих тригонометрических функций (или выразить их через значения тригонометрических функций острых углов): а) 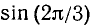
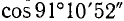
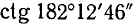
Решение:
а) 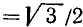
б) 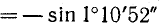
в) 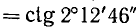
Пример:
Найти 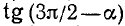
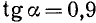
Решение:
Сформулируем теперь общее правило приведения:
1) если угол а откладывается от вертикальной оси (углы 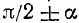
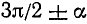
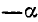
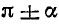
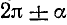
2) если приводимая функция имеет отрицательное значение, то нужно соответствующую функцию угла а взять со знаком минус, если же приводимая функция имеет неотрицательное значение, то нужно соответствующую функцию угла а взять со знаком плюс.
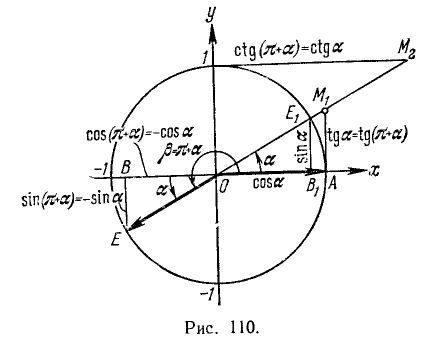
Проиллюстрируем это правило на примере угла 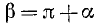
Итак, на рис. 110 угол 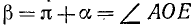
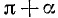
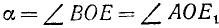
1) соответствующие названия тригонометрических функций; 2) знаки приводимых тригонометрических функций.
1) Так как угол а откладывается от горизонтальной оси (угол 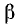
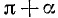
2) 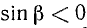
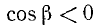
Учитывая 1) и 2), имеем
так как 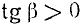
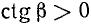
Мы пришли к формулам (106.2) и (106.3). Рекомендуем читателю проиллюстрировать на чертеже типа рис. 110 правило приведения для остальных углов (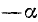
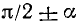

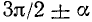
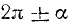
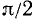
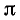
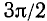
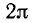
Объединим полученные для формул приведения результаты в следующую таблицу.
Для произвольного угла 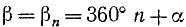
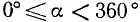
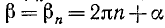
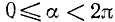

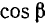
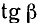
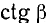
Пример:
Дан угол 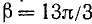

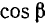
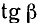
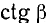
Решение:
Представим данный угол в виде 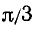
Заметим, что тангенс и котангенс можно было бы вычислить и так:
Пример:
Найти 
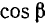
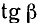
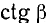
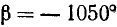
Решение:
Представим данный угол в виде
Применив формулы (104.1), получим
Тангенс и котангенс найдем следующим образом:
Пример:
Имеем угол 

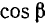
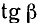
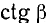
Решение:
Представим данный угол в виде
Применив формулы (104.1) и (106.1), получим
Пример:
Найти 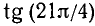
Решение:
Пример:
Найти 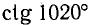
Решение:
Пример:
Решение:
Применив формулы приведения, получим в левой части предполагаемого тождества
т. е. левая часть равна 1. Мы пришли к верному равенству, что и доказывает наше тождество.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института