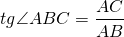Что означает значок процента с двумя нулями

Что такое 1 промилле?

Что такое 1 промилле? Как найти 1 промилле? Что измеряют в промилле?

1 проми́лле — это одна тысячная часть числа.

Для обозначения промилле существует специальный знак — ‰ (знак процента с двумя нулями).

Вместо «1 промилле» пишут «1 ‰».

Слово «промилле» происходит от латинского «pro mille» (за тысячу, с тысячи).

Так как промилле — это одна тысячная часть числа, то все число — это 1000 ‰.

Промилле — десятые части процента, то есть

Чтобы найти 1 промилле от числа, надо число разделить на тысячу.

1 ‰ от 563 равен 563:1000=0,563;

1 ‰ от 7204 равен 7204:1000=7,204;

1 ‰ от 65000 равен 65000:1000=65.

Для некоторых величин тысячная часть числа имеет свое название.

1 ‰ от 1 килограмма равен 1 грамму;

1 ‰ от 1 тонны равен 1 килограмму;

1 ‰ от 1 километра равен 1 метру.

Некоторые величины традиционно измеряют именно в промилле.

Например, соленость воды, уклон железнодорожного пути, уклон дороги, уклон кровли, естественный прирост населения.

Соленость океанской воды составляет около 35 ‰. Это означает, что в одном литре такой воды содержится 35 граммов солей.

Соленость морской воды разная: самая высокая — 40-42 промилле — в Красном море, в Баренцевом — всего 5 промилле.

Уклон железнодорожного полотна измеряют тысячными долями, но, в отличие от солености воды, их так и называют — тысячные ( а не промилле).

Если длина горизонтального отрезка AB равна 1000 метров, то уклон 11 тысячных означает, что высота AC, на которую поднимется состав, следующий по железной дороге из пункта B в пункт C, равна 11 метрам.

В старших классах вы узнаете, что угол ABC можно выразить через длины отрезков AC и BC как тангенс угла ABC:

Источник

что этот знак обозначает ‰

Проми́лле (лат. pro mille — за тысячу) [1] — одна тысячная доля, 1/10 процента.

Обозначается (‰). Используется для обозначения количества тысячных долей чего-либо в целом. Происходит (как и процент) от написания простой дробью: 27/1000 → 27‰; количество нулей в обозначении (3 нуля) соответствует количеству нулей в числе 1000.

Символ можно ввести на компьютере с Windows с помощью Alt-0137: при включённом NumLock удерживая левый Alt набрать на цифровом блоке клавиатуры 0137.

Так,
1 ‰ = 1⁄1000 = 0,001 = 0,1 %
10 ‰ = 1 %
0 ‰ = 0
0,07 ‰ = 0,00007
30 ‰ = 0,03
45,1 ‰ = 0,0451
1000 ‰ = 1
2000 ‰ = 2
10 ‰ = 0,01

Величина в промилле от массы, выраженной в килограммах, эквивалентна массе в граммах. От массы в тоннах — килограммам.

Уровень содержания алкоголя в крови человека также часто выражается в промилле.

Представив рельс как гипотенузу прямоугольного треугольника, один из катетов которого имеет длину 1000 метров и параллелен горизонту, увидим, что второй катет будет равен высоте, на которую поднимется состав, проехав (почти) 1 километр. Отношение второго катета к первому на практике часто представляет собой очень малую величину, поэтому его удобно выражать в тысячных. Уклон в 8 ‰ означает, например, что, проехав 1 километр, состав поднимется на высоту 8 метров (тангенс угла подъёма при этом составляет 0,008, то есть собственно угол подъёма равен arctg 0,008 ≈ 0,46°).

Однако в американской практике уклон пути измеряют в процентах, используя десятичные дроби. Возможно, это связано с тем, что в Америке используется английская система мер, в которой соотношения между единицами расстояния (в частности, милями, ярдами и футами) не кратны 1000.

Источник

Процент с 3 нулями

Этот странный знак процента – Промилле. Дословно с латинского — на тысячу (per mille) — одна тысячная доля, используется для обозначения количества тысячных долей чего-либо в целом.

Если процент — % обозначает сотые доли от числа, то промилле — ‰ обозначает десятые доли от процента и тысячные доли от числа. Более наглядно выглядит так:

1 ‰ = 1⁄1000 = 0,1 % = 0,001

Наиболее известное применение – показатель уровня содержания алкоголя в крови человека.

В географии с 1978 был принят международный стандарт по измерению солености морей и океанов в промилле.

Обобщенно в вышеуказанных примерах промилле — это количество грамм какого-либо вещества на литр жидкости. Иными словами, концентрация раствора.

В строительстве промилле применяют для точного обозначения уклона железнодорожного пути, дороги, кровли и пр.

P.S. В программных продуктах от Microsoft есть возможность быстро напечатать символ промилле с помощью Alt-0137: при включённом Num Lock, удерживая Alt, набрать на цифровом блоке клавиатуры 0137.

Дубликаты не найдены

Интересно, но при попытке повторить произошло колдунство: открылась стартовая страница FF

Комментарий дня

Хех, мы двумя парами в кино пришли, купили центр зала (они дороже рублей на 150 чтоль были), пока брали девочкам мороженку, мальчикам пиво и попкорн рекламе, зал уже заполнился и только началась реклама. Протискиваемся к местам, а они заняты 4 мамзелями, постарше нас, но быдловатыми. Тип че пришли, места наши, ваши вон, на первом ряду гыгыгы. Деревня с самогоном блин. Народ бухтит, тип свалите. Пошли к администраторам — девок пересадили. Ток эти *** воду вылили на все 4 места. А сами ушли на первый ряд.

В общем нам прилетел бонус в виде просмотра фильма в вип зале, через 30 минут правда, два ведра попкорна и пару пива. А девок потом видели в ТЦ, их охрана держала и судя по всему ждали полицию)))

Больше всего реакция окружающих понравилась — идите сядьте вперед, че вы всем мешаете.

Рекомендуемое сообщество

Сообщество о ремонте, обслуживании автотранспорта, новости, советы и тематические истории.

Величина в промилле от массы, выраженной в килограммах, эквивалентна массе в граммах; от массы в тоннах — килограммам.

Содержание

ppm [ править | править код ]

Применение [ править | править код ]

Есть некоторые величины (доли), традиционно измеряемые в промилле.

Например, фраза «солёность воды составляет 11 ‰ (одиннадцать промилле)», это то же самое, что и 1,1 %, и означает, что из общей массы воды 0,011 (11 тысячных) занимают соли. Так, если взять 1 кг (1000 г) солёной воды солёностью в 11 ‰, то в такой воде будет 11 г солей.

Уровень содержания алкоголя в крови человека также часто выражается в промилле.

Уклон [ править | править код ]

Представив рельс как гипотенузу прямоугольного треугольника, один из катетов которого имеет длину 1000 метров и параллелен горизонту, увидим, что второй катет будет равен высоте, на которую поднимется состав, проехав чуть больше 1 километра. Отношение второго катета к первому на практике часто представляет собой очень малую величину, поэтому его удобно выражать в тысячных. Уклон в 8 ‰ означает, например, что, проехав 1 километр, состав поднимется на высоту 8 метров (тангенс угла подъёма при этом составляет 0,008, то есть собственно угол подъёма равен arctg 0,008 ≈ 0,46°).

Однако в американской практике уклон пути измеряют в процентах, используя десятичные дроби. Возможно, это связано с тем, что в Америке используется английская система мер, в которой соотношения между единицами расстояния (в частности, милями, ярдами и футами) не кратны 1000.

Онлайн калькулятор для перевода промилле в проценты и наоборот.

Промилле (знак ‰) — одна тысячная доля, 1⁄10 процента используется для обозначения количества тысячных долей чего-либо в целом. Знак промилле образован от знака процента (%) добавлением ещё одного «нуля».

Источник

Что такое процент? Формула процентов. Проценты

Что означает процент

В переводе с латыни процент (per centum) означает «на сотню» или «сотая», то есть одна сотая доля числа. Принято обозначение знаком «%». Процент принято использовать, когда хотят указать точную долю чего-либо к одной единице. 100% – 1, соответственно, 25% – это 0,25 и 25/100.

Также с помощью этого понятия можно сравнивать разные величины, предварительно указывая, из какого целого нужно вычесть проценты. Скажем, доход больше расхода на 25%, стоимость авиабилетов снизилась на 3%, если сравнить с прошлогодними расценками, книга «Орден феникса» на 35% толще, чем «Кубок огня» и так далее. Бывает ситуация, когда процент получается больше 100, это значит, что доля вышла больше 1.

В финансах процент является оплатой заемщика кредитору за деньги, полученные на время. Процентщик – это человек, выдающий деньги на время под определённый процент. Человек, который брал кредит, в дальнейшем будет вынужден вернуть изначально взятую сумму, да ещё и доплатить сверху.

В бизнесе существует определение «работа за проценты», в таком случае размер заработной платы напрямую зависит от прибыли или оборота. Этот принцип несёт в себе как позитивные возможности, так и определенный риск, ведь с одной стороны можно заработать много, а можно не заработать ничего. Без процентов невозможно представить функционирования не только бизнеса, но и банков с бухгалтерией.

Процент элементарно понять благодаря самому знаку «%» – в символе скрыт весь смысл. Наклонная черта / означает деление, а два небольших ноля на 100. Вот и выходит, что 20% – это 20 делить на 100, получается 0,2.

Видео

Перевод процента в десятичную дробь

Пожалуй, нет ничего проще, чем видоизменить процент в десятичную дробь.Для расчета вам понадобятся проценты, которые разделить на 100.

Если перед вами стоит цель получить десятичную дробь из 75 %, то элементарнее задачи просто не придумаешь.

Увеличение, уменьшение числа на заданное количество процентов

Школьники должны усвоить, что такое проценты, как считать их и решать разнообразные задачи. Для этого нужно понимать, как увеличивается или уменьшается число на N%.

Зачастую даются задания, да и в жизни нужно узнать, чему будет равно число, увеличенное на заданное количество процентов. К примеру, дано число Х. Нужно узнать, чему будет равно значение Х, если его увеличить, допустим, на 40%. Сначала нужно перевести 40% в дробное число (40/100). Итак, результатом увеличения числа Х станет: Х + 40% ∙ Х= ( 1+40 /₁₀₀) ∙ Х = 1,4 ∙ Х. Если вместо Х подставить любое число, возьмем, к примеру, 100, тогда все выражение будет равно: 1,4 ∙ Х = 1,4 ∙ 100 = 140.

Встречаются задания, где нужно узнать, на сколько процентов увеличилось число.

К примеру, дана задача: Машинист ехал по одному участку пути со скоростью 80 км/ч. На другом участке скорость поезда возросла до 100 км/ч. На сколько процентов возросла скорость поезда?

Предположим, 80 км/ч – 100%. Тогда производим расчеты: (100% ∙ 100 км/ч) / 80 км/ч= 1000 : 8 = 125%. Получается, что 100 км/ч – это 125%. Чтобы узнать, на сколько увеличилась скорость, нужно вычислить: 125% — 100% = 25%.

Ответ: на 25% увеличилась скорость поезда на втором участке.

Изменение числа на сколько-то процентов

Когда говорят, что число увеличилось на \( \displaystyle x\), это значит, что к числу надо прибавить \( \displaystyle x\).

Если же число уменьшилось на \( \displaystyle x\), это значит, что из числа надо вычесть \( \displaystyle x\).

Рассмотрим пример:

Цена холодильника в магазине за год увеличилась на \( \displaystyle 5\%\). Какой стала цена, если изначально холодильник стоил \( \displaystyle 12500\)р?

Решение:

Для начала определим, на сколько рублей изменилась (в данном случае – увеличилась) стоимость холодильника. По условию – на \( \displaystyle 5\%\). Но \( \displaystyle 5\%\) от чего? Конечно же, от самой начальной стоимости холодильника (\( \displaystyle 12500\) р). Получается, что нам нужно найти \( \displaystyle 5\%\) от \( \displaystyle 12500\)р:

\( \displaystyle 0,05\cdot 12500=625\).

Теперь мы знаем, что цена увеличилась на \( \displaystyle 625\)р. Остается только, согласно правилу, прибавить к начальной стоимости величину изменения:

Новая цена \( \displaystyle=12500+625=13125\) рублей.

Ответ: \( \displaystyle 13125.\)

Еще пример (постарайся решить самостоятельно):

Книга «Математика для чайников» в магазине стоит \( \displaystyle 360\)р. Во время акции все книги продаются со скидкой \( \displaystyle 15\%.\). Сколько теперь придется заплатить за эту книгу?

Решение:

Что такое скидка, ты наверняка знаешь? Скидка в \( \displaystyle 15\%.\) означает, что стоимость товара уменьшили на \( \displaystyle 15\%.\).

На сколько уменьшилась стоимость книги (в рублях)? Нужно найти \( \displaystyle 15\%.\) от начальной ее стоимости в \( \displaystyle 360\)р:

\( \displaystyle 0,15\cdot 360=54\).

Цена уменьшилась, значит нужно из начальной стоимости вычесть то, на сколько она уменьшилась:

Новая цена \( \displaystyle=360-54=306\) рублей.

Ответ: \( \displaystyle 306\).

Правда ведь просто?

Но есть способ сделать это решение еще проще и короче!

Рассмотрим пример:

Увеличьте число \( \displaystyle x\) на \( \displaystyle 23\%\).

Чему равны \( \displaystyle 23\%\) от \( \displaystyle x\)? Как мы уже выяснили раньше, это будет \( \displaystyle 0,23x\).

Теперь увеличим само число x на эту величину:

Получается, что в результате мы к десятичной записи \( \displaystyle 23\%\) прибавили \( \displaystyle 1\) и умножили на число \( \displaystyle x\). Обобщим это правило:

Пусть нам нужно увеличить число \( \displaystyle x\) на \( \displaystyle p\%\).

\( \displaystyle p\%\) от числа \( \displaystyle x\) – это \( \displaystyle \frac

<100>\cdot x\).

Тогда новое число будет равно: \( \displaystyle x+\frac

<100>\cdot x=x\left( 1+\frac

<100>\right)\).

Чтобы увеличить число на \( \displaystyle p\%\), нужно умножить его на \( \displaystyle \left( 1+\frac

<100>\right)\).

Например, увеличим число \( \displaystyle 136\) на \( \displaystyle 28\%\):

\( \displaystyle 136\cdot \left( 1+0,28 \right)=136\cdot 1,28=\text<174>\text<,08>\).

Примеры задач на проценты

1. Сколько процентов от числа 36 составляет число 9?

По формуле нахождения процента от числа, нужно 9 умножить на 100 и поделить на 36.

Ответ: число 9 составляет 25% от 36.

2. Вычислить число С, которое составляет 10% от 40.

По формуле нахождения числа по его проценту, нужно 40 умножить на 10 и результат разделить на 100.

Ответ: число 4 составляет 10% от 40.

3. Первый партнер вложил в бизнес 4500 рублей, второй – 3500 рублей, третий – 2000 рублей. Они получили прибыль 2400 рублей. Прибыль они разделили поровну. Сколько в рублях потерял первый партнер, по сравнению с тем, сколько бы он получил, если бы они разделили доход согласно проценту вложенных средств?

Итак, вместе они вложили 10 000 рублей. Доход на каждого составил равную долю по 800 рублей. Чтобы узнать, сколько должен был получить первый партнер и сколько он, соответственно, потерял, нужно узнать процент вложенных средств. Затем нужно узнать, сколько в рублях прибыли составляет этот вклад. И последнее — вычесть 800 рублей из полученного результата.

Ответ: первый партнер потерял 280 рублей при разделе прибыли.

Процентный пункт

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Найти от 10 см

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби

Получили 0,1. Теперь 0,1 умножаем на числитель дроби

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

Теперь полученный результат умножаем на 50

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти от 300 рублей, а решать такие задачи для нас пока проще

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

Ответ: 384 костюмов нового фасона выпустила фабрика.

Основная связь между десятичными дробями и процентами

Если нужно перевести десятичную дробь в проценты, то ее умножают на 100 и дописывают знак %.

Если нужно совершить обратную операцию — перевести проценты в десятичную дробь, то число делят на 100%.

Переведите 56% в десятичную дробь. Объяснение. Чтобы перевести проценты в десятичную дробь, нужно число процентов разделить на 100%. При делении на 100 по правилу отсчитываем в числе количество знаков справа налево, равное количеству нулей, и ставим запятую. Значит, при делении на сто запятую ставим, отсчитав два знака влево от конца записи числа. Получим 0,56. 56%=56%:100%=56:100=,56. Ответ: 0,56.

Задачи на проценты подробнее

Что такое процент? Откуда взялось это слово?

Все очень просто. Слово процент произошло от латинского per cent– на сотню, и означает оно «сотая доля» или «сотая часть».

То есть один процент любого числа – это одна сотая этого числа.

И все. Этого достаточно, чтобы решать задачи, в которых присутствует это противное слово «процент».

Например: чему равны \( \displaystyle 34\%\) от числа \( \displaystyle 120\)?

Прочтем это задание по-другому: чему равны \( \displaystyle 34\) сотых доли числа \( \displaystyle 120\)?

Элементарно, правда? Нужно разделить число \( \displaystyle 120\) на \( \displaystyle 100\) частей (чтобы узнать, чему равна одна сотая доля – один процент) и взять \( \displaystyle 34\) таких части:

\( \displaystyle \frac<120><100>\cdot 34=1,2\cdot 34=40,8\).

Сколько процентов содержится в числе?

Снова перефразируем вопрос, заменив слово «процент» на «сотую часть»: Сколько сотых частей находится в числе?

Ответ сразу становится очевидным: в любом числе или предмете находится ровно сто сотых частей (то есть, если разделить число или предмет на \( \displaystyle 100\) частей, сколько будет этих частей?

Очевидно же, что \( \displaystyle 100\)).

Разберем еще несколько примеров

Метод решения задач с процентами

Все соотношения и формулы, полученные для решения задач с процентами, выводятся из пропорции

Данные задачи на проценты можно записать в виде следующих соотношений:

все — 100%часть — часть в %

которые можно записать в виде пропорции

Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.

Способы нахождения процента

Правило нахождения процентов от числа: Чтобы найти процент от числа, нужно перевести процент в десятичную дробь и умножить на заданное число.

Правило нахождения числа по его проценту: Чтобы найти число по его процентам, нужно:проценты числа перевести в десятичную дробь;заданное число разделить на полученную дробь.

Процентное отношение двух чисел

Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.

Задача. Завод по годовому плану должен выпустить продукции на сумму 1 250 000 руб. За 1-ый квартал он выпустил её на сумму 450 000 руб. На сколько процентов выполнен заводом годовой план за 1-ый квартал?

Ответ: За 1-ый квартал план выполнен на 36%.

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Источник