Что означает знак приставки в информатике
Глава 2. Приставки к единицам измерения в информатике.
Вспомним немного информатики из курса средней школы.
Всю информацию можно закодировать определённым кодом. В технике способ кодирования информации осуществляется с помощью двух символов: <0,1>. Для удобства использования такого алфавита договорились называть любой из его знаков словом «бит» (от английского «binary digit»- двоичный знак). Потому можно ввести определение: «Бит – это наименьшая единица измерения объема информации».
Мы привыкли к обычным приставкам, перед единицами измерения то есть: КИЛО, МЕГА, ГИГА и т.д.
Но есть подвох. Если мы под приставкой КИЛО понимаем 1000 = 10 * 10 * 10, то есть 10 в третьей степени, то в информатике 10 не является базисом умножения. В информатике базисом является цифра «2».
Как же получить цифру 1 000 из двоек. Попробуйте сделать возведите 2 в степень 10. Кто не помнит про степень, скажу проще, умножьте 2 на 2, 10 раз или так 2*2*2*2*2*2*2*2*2*2 = 1 024. То есть получили, что (2 бита) 10 есть число равное 1 024 бита.
Если посмотреть на 1 000 и 1 024, то можно их условно приравнять.
Попробуйте, возведите 2 в 20 степень, или перемножьте 2-ку 20-ть раз. Получим 1024*1024 = 1 048 576 примерно можно приравнять к 1 000 000, то есть, получаем приставку МЕГА.
1 024 Байт = 1 Кбайт.
1 024 Кбайт = 1 Мбайт.
1 024 Мбайт =1 Гбайт.
| Значения единиц измерения информации | ||
| Название | Величина | Значение |
| Килобайт | 2 10 | 1024 байта |
| Мегабайт | 2 20 | 1024 килобайта или 1 048 576 байт |
| Гигабайт | 2 30 | 1024 мегабайта или 1 073 741 824 байта |
| Терабайт | 2 40 | 1024 гигабайта или 1 099 511 627 776 байт |
Теперь перенесёмся ближе к нашей работе и рассмотрим пример с битрейтом в mp3 файле.
Битрейт это не скорость воспроизведения, это количество информации, кодирующее 1 секунду музыки.
Вопрос? Сколько поместится музыки на Flash плеер объёмом 256 МБ, если записывать музыку с битрейтом 192 Кбит/сек?
Битрейт 192 Кбит/сек.
То есть 1 секунда музыки кодируется 192 Килобитами. Нам нужно перейти от секунд к минутам, а от Килобит к МегаБайтам.
192Кбит = (Переведём Килобиты в Килобайты то есть, разделим 192 на 8) = 24 КБайт.
1 минута = 60 секунд = 60*24 КБ = 1 440 КБ = примерно = 1,4 МБ.
Получили, что 1 минута музыки кодируется 1,4 МБ.
Для того чтобы найти, сколько минут поместится на плеер определённого объёма, необходимо разделить объём плеера на размер, занимаемый 1 минутой.
256 МБ / 1,4 МБ = 182 минуты или примерно 3 часа музыки.
Ответ: На Flash плеер 256 МБ поместится примерно 3 часа музыки, если записывать её с битрейтом 192 Кбит/сек.
Я надеюсь, что теперь не будет проблем с такими изречениями, как скорость передачи данных по каналу CSD 9.6 Кбит/сек, битрейт и сколько музыки поместится на диск 700 МБ, да и вообще, надеюсь, что вы получили некоторый базис в том, чем вы оперируете каждый день.
И ещё некоторая информация:
Компьютерная терминология становится более точной: международная организация International Electrotechnical Commission, занимающаяся созданием стандартов для отрасли электронных технологий, утвердила ряд новых приставок для единиц измерения количества данных.
Используемые в настоящее время заимствованные из метрической системы приставки кило, мега, гига и другие основаны на степенях числа 10, а не двойки, являющейся основой двоичного исчисления, на котором основаны современные компьютеры.
Комиссия утвердила приставки киби, меби, гиби, теби, пеби и эксби (kibi, mebi, gibi, tebi, pebi и exbi) для обозначения коэффициентов 2 в степени 10, 2 в степени 20 и т.д.
Дата добавления: 2015-07-26 ; просмотров: 11 ; Нарушение авторских прав
Что означает знак приставки в информатике
Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
Байт – основная единица измерения количества информации.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события (N=4).
По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (2 5 =32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log2101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Задача 7.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.
СТРАННАЯ ДЕВОЧКА
Но станет всё совсем обычным,
Когда поймёте наш рассказ.
С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе.
Объём памяти компьютера измеряется в байтах. Каждый байт может выражать букву, число, пробел, знак препинания или какой-либо другой символ. Количество символов, которые компьютер может хранить в оперативной памяти, меняется в широких пределах от вида компьютера и его модели.
Объём памяти, хотя он и измеряется в байтах, обычно выражается в килобайтах. Слово «килобайт», вообще говоря, означает «1000 байт». (Напомним, что приставка «кило» означает «тысяча».)
Фактически же килобайт равен 1024 байтам: 1 Кбайт = 1024 байт.
Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов.
Объём памяти первых микрокомпьютеров составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128, 256, 512, 1024 Мб и более
Объём памяти новейших компьютеров так велик, что она выражается в гигабайтах, т. е. в миллиардах байтов.
1 Мбайт = 1024 Кбайт = 1 048 576 байт.
Итак, каждый символ алфавитно-цифровой информации представляется в компьютере кодом из восьми двоичных цифр. Следовательно, каждый символ в компьютере имеет код объёмом 1 байт.
Информатика и образование
имеет в двоичной форме объём 25 байт: 23 буквы и 2 символа «пробел» по 1 байту.
61 байт * 45 строк = 2745 байт.
Так как в книге 258 страниц текста и на каждой странице в среднем по 2745 байт информации, то объём алфавитно-цифровой информации в книге
2745 байт * 258 страниц = 708210 байт » 692 Кбайт
Таким образом, текст книги имеет объём около 692 Кбайт.
Перевод чисел
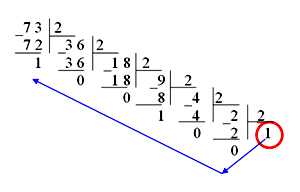
Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.
А вот как происходит перевод двоичного числа в десятичное:
ДРОБНЫЕ ЧИСЛА В ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ
В любой системе счисления нужно уметь представлять не только целые числа, но и дробные. С математической точки зрения это ординарная задача, которая давно решена. Однако с точки зрения компьютерной техники это далеко не тривиальная проблема, во многом связанная с архитектурой компьютера. Ресурсы компьютеров не бесконечны, и основной трудностью является представление периодических и непериодических дробей. Следовательно, такие дроби следует округлять, задавать класс точности участвующих (и могущих появиться в результате вычислений!) чисел без потери точности вычислений, а также следить за тем, чтобы потеря точности не произошла при переводе чисел из одной системы счисления в другую. Особенно важно аккуратно производить вычисления при операциях с плавающей точкой.
Запишем формулу представления дробного числа в позиционной системе счисления:
В случае десятичной системы счисления получим:
Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
· Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
· Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
· В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
· Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
.792 • 2 = 1 .584
Получим: 206,11610=11001110,00011100112
Таблицу степеней первых восьми отрицательных степеней двойки
Двоичная арифметика
Над числами в двоичной системе счисления можно выполнять арифметические действия.
ТЫ, Я и ИНФОРМАТИКА
Обозначения в логических операциях
Обозначения для логических связок:
отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);
конъюнкция (логическое умножение, логическое И) обозначается /\
дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/
следование (импликация) обозначается → (например, А → В);
тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);
символ 1 (единица) используется для обозначения истины (истинного высказывания);
символ 0 (ноль) используется для обозначения лжи (ложного высказывания).
Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) \/ В равносильны, а А /\ В и А \/ В – нет (значения выражений разные, например, при А = 1, В = 0).
Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А \/ В \/ С \/ D означает то же, что и
Возможна запись А \/ В \/ С вместо (А \/ В) \/ С. То же относится и к конъюнкции: возможна запись А /\ В /\ С вместо (А /\ В) /\ С.
Свойства логических операций
Общие свойства логических операций
Для набора из n логических переменных существует ровно 2n различных значений. Таблица истинности для логического выражения от n переменных содержит n+1 столбец и 2n строк.
Дизъюнкция
Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.
Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
Конъюнкция
Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.
Значение конъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.
Простая дизъюнкция принимает значение 0 (ложь) ровно на одном наборе значений переменных.
Импликация
Импликация A →B равносильна дизъюнкции (¬А) \/ В. Эту дизъюнкцию можно записать и так: ¬А \/ В.
Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A →B истинна при любом значении B.
Логика
НЕКОТОРЫЕ
СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ
1. Обозначения
1.1. Обозначения для логических связок (операций):
a) отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);
b) конъюнкция (логическое умножение, логическое И) обозначается /\
(например, А /\ В) либо & (например, А & В);
c) дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/
(например, А \/ В);
d) следование (импликация) обозначается → (например, А → В);
e) тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);
f) символ 1 используется для обозначения истины (истинного высказывания); символ 0 – для обозначения лжи (ложного высказывания).
1.2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) \/ В равносильны, а А /\ В и А \/ В – нет (значения выражений разные, например, при А = 1, В = 0).
1.3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А \/ В \/ С \/ D означает то же, что и
Возможна запись А \/ В \/ С вместо (А \/ В) \/ С. То же относится и к конъюнкции: возможна запись А /\ В /\ С вместо (А /\ В) /\ С.
2. Свойства
Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.
2.1. Общие свойства
2.2.Дизъюнкция
2.3. Конъюнкция
2.4. Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
2.5. Импликация