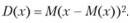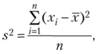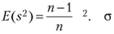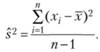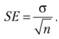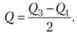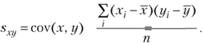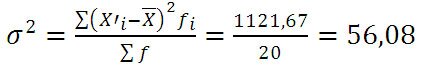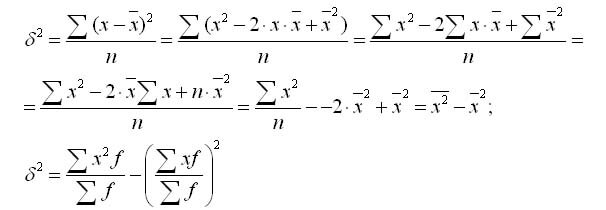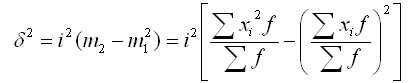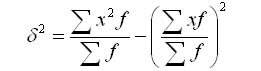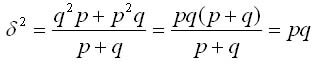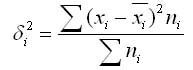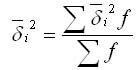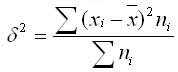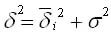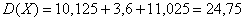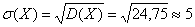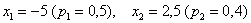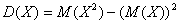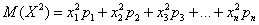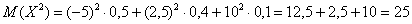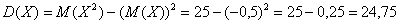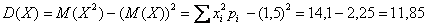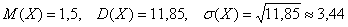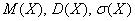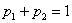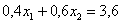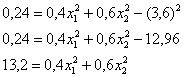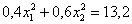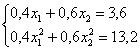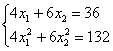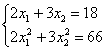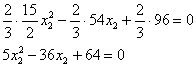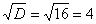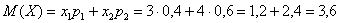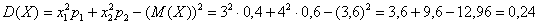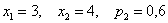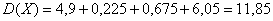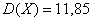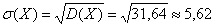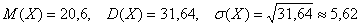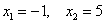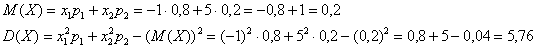Что показывает дисперсия наблюдаемой величины
Дисперсия и ее оценка
Определение дисперсии случайных величин
Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.
В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:
где М(х) – математическое ожидание, а D(х) – дисперсия.
На основе данной формулы можно вывести другую, которая дает оценку дисперсии:
В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных. Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.
Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:
Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности. Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения. При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:
Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.
Характеристика оценивания стандартного отклонения
Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением. Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности. Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:
где SE – стандартная ошибка.
Данная статистика необходима для интервальной оценки исследуемой случайной величины.
Характеристика оценки полумежквартильного интервала
Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.
Квартиль – это вариант названия квантиля распределения.
При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:
Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.
Характеристика ковариации
Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:
Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах. Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция». Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.
Дисперсия, виды и свойства дисперсии
Понятие дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
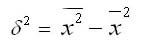
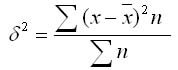
Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию
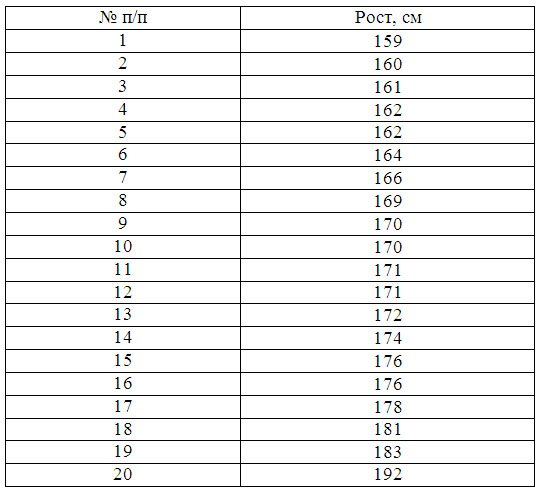

X min–минимальное значение группировочного признака;
n – количество интервалов:
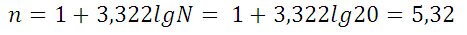
Составим интервальную группировку
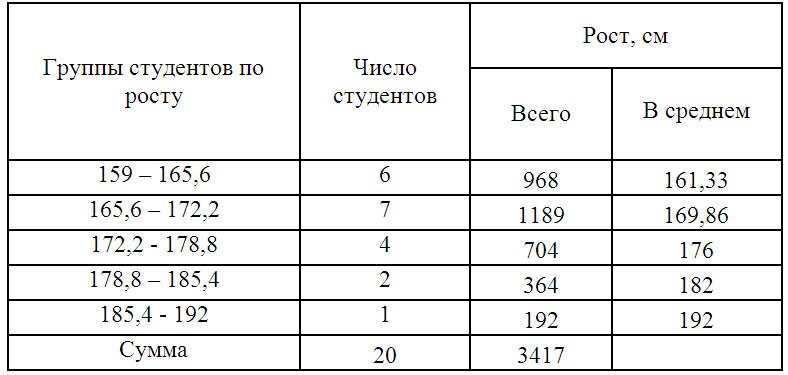
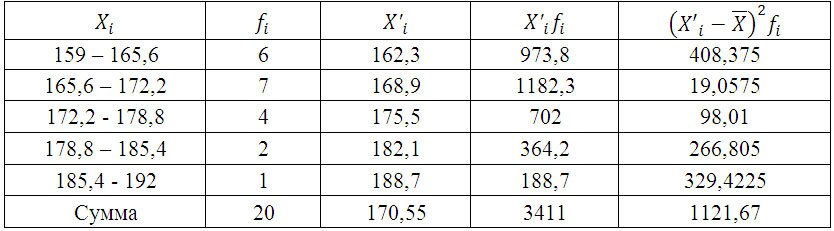
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
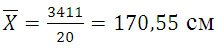
Формулу дисперсии можно преобразовать так:
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:
Подставляя в данную формулу дисперсии q =1- р, получаем:
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя;
ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.
Свойства дисперсии
1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Дисперсия дискретной случайной величины.
Среднее квадратическое отклонение
Итак, продолжаем. В предыдущей статье мы выяснили, насколько полезно знать математическое ожидание, однако только этой характеристики ещё не достаточно для исследования случайной величины. Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, его средний результат будет точно таким же, как и у первого стрелка! Эту ситуацию условно иллюстрируют следующие случайные величины:
«Снайперское» математическое ожидание равно 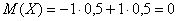
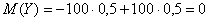
Таким образом, возникает потребность количественно оценить, насколько далеко рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.
Посмотрим, как определяется эта числовая характеристика на одном из примеров 1-й части урока:
Там мы нашли неутешительное математическое ожидание 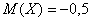
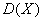
Выясним, насколько далеко «разбросаны» выигрыши/проигрыши относительно среднего значения. Очевидно, что для этого нужно вычислить разности между значениями случайной величины и её математическим ожиданием:
–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5
Теперь вроде бы нужно просуммировать результаты, но этот путь не годится – по той причине, что колебания влево будут взаимоуничтожаться с колебаниями вправо. Так, например, у стрелка-«любителя» (пример выше) разности составят 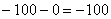
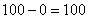
Чтобы обойти эту неприятность можно рассмотреть модули разностей, но по техническим причинам прижился подход, когда их возводят в квадрат. Решение удобнее оформить таблицей: 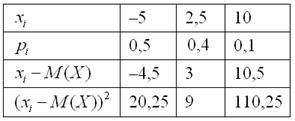
И здесь напрашивается вычислить средневзвешенное значение квадратов отклонений. А это ЧТО такое? Это их математическое ожидание, которое и является мерилом рассеяния:
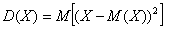
Вспоминаем, как находить матожидание. Перемножаем квадраты разностей на соответствующие вероятности (продолжение таблицы):
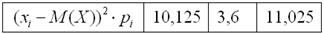
и суммируем результаты:
Не кажется ли вам, что на фоне выигрышей 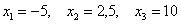
Иногда это значение называют стандартным отклонением.
В чём его смысл? Если мы отклонимся от математического ожидания 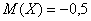
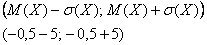
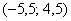
Однако так сложилось, что при анализе рассеяния почти всегда оперируют понятием дисперсии. Давайте разберёмся, что она означает применительно к играм. Если в случае со стрелками речь идёт о «кучности» попаданий относительно центра мишени, то здесь дисперсия характеризует две вещи:
Во-первых, очевидно то, что при увеличении ставок, дисперсия тоже возрастает. Так, например, если мы увеличим 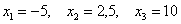
Второй, более интересный момент состоит в том, что дисперсия характеризует стиль игры. Мысленно зафиксируем игровые ставки на каком-то определённом уровне, и посмотрим, что здесь к чему:
Игра с низкой дисперсией – это осторожная игра. Игрок склонен выбирать самые надёжные схемы, и в ситуации неопределённости не ставит слишком большие деньги. Например, система «красное/чёрное» в рулетке (см. Пример 4 статьи Случайные величины).
Игра с высокой дисперсией. Её часто называют дисперсионной игрой. Это авантюрный или агрессивный стиль игры, где игрок выбирает «адреналиновые» схемы. Вспомним хотя бы «Мартингейл», в котором на кону оказываются суммы, на порядки превосходящие «тихую» игру предыдущего пункта.
То же самое происходит на Форексе, других биржах и так далее – примеров масса.
Причём, во всех случаях не важно – на копейки ли идёт игра или на тысячи долларов. На любом уровне есть свои низко- и высокодисперсионные игроки. Ну а за средний выигрыш, как мы помним, «отвечает» математическое ожидание.
Наверное, вы заметили, что нахождение дисперсии – есть процесс длительный и кропотливый. Но математика щедрА:
Формула для нахождения дисперсии
Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой: 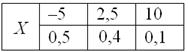
и найденное матожидание 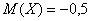
Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание 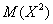
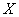
В данном случае:
Таким образом, по формуле:
Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).
Осваиваем технику решения и оформления:
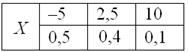
Дискретная случайная величина задана своим законом распределения:
Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла.
Можете представлять себе несколько лампочек с числами, которые загораются в дурдоме с определёнными вероятностями 🙂
Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения 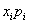
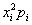
Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: 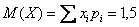
Дисперсию вычислим по формуле:
И, наконец, среднее квадратическое отклонение:
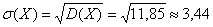
Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе:
вот здесь уже трудно ошибиться 🙂
Ответ:
Желающие могут ещё более упростить свою жизнь и воспользоваться моим калькулятором (демо), который не только моментально решит данную задачу, но и построит тематические графики (скоро дойдём). Программа доступна за символическую плaтy. Спасибо за поддержку проекта!
Пара заданий для самостоятельного решения:
Вычислить дисперсию случайной величины 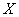
И аналогичный пример:
Дискретная случайная величина задана своим законом распределения:
Найти
Да, значения случайной величины бывают достаточно большими (пример из реальной работы), и здесь по возможности используйте Эксель. Как, кстати, и в Примере 7 – это быстрее, надёжнее и приятнее.
Решения и ответы внизу страницы.
В заключение 2-й части урока разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:
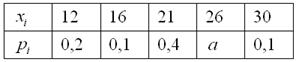
Дискретная случайная величина 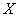
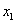
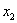
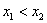
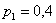
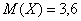
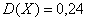
Найти 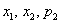
Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:
и поскольку 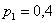
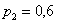
Осталось найти 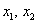
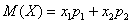
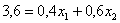
ОК, едем дальше. По формуле вычисления дисперсии:
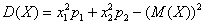
или:
О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:
Десятичные дроби – это, конечно, полное безобразие; умножаем оба уравнения на 10:
и делим на 2:
Вот так-то лучше. Из 1-го уравнения выражаем:
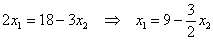
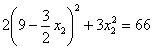
Возводим в квадрат и проводим упрощения: 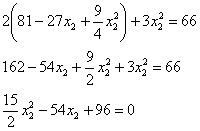
Умножаем на 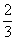
В результате получено квадратное уравнение, находим его дискриминант:
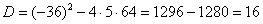
и у нас получается два решения:
1) если 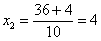
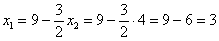
2) если 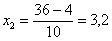
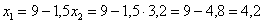
Условию 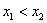
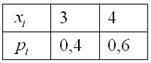
и выполним проверку, а именно, найдём матожидание:
и дисперсию:
В результате получены исходные значения, что и требовалось проверить.
Ответ:
Следует отметить, что это технически трудное задание, и поэтому в нём следует проявлять повышенное внимание. Потренируйтесь самостоятельно:
Случайная величина 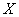
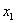
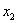
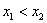
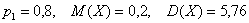
Тут вычисления попроще.
Жду вас в третьей, заключительной части урока, где мы познакомимся с многоугольником и функцией распределения. Её лучше изучить как можно скорее!
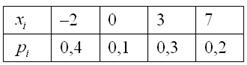
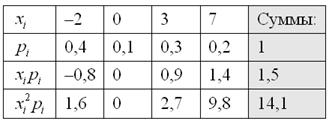
Пример 7. Решение: вычислим математическое ожидание: 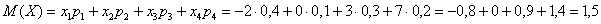
Вычислим дисперсию по определению: 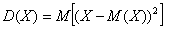
Заполним расчётную таблицу: 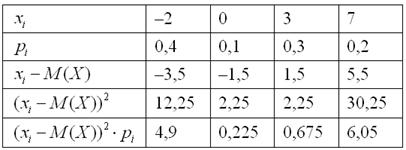
Таким образом:
Ответ:
Пример 8. Решение: случайная величина может принять только 5 значений, поэтому: 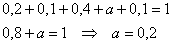
Заполним расчётную таблицу: 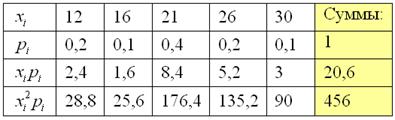
Математическое ожидание: 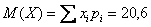
Дисперсию вычислим по формуле: 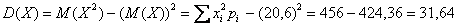
Среднее квадратическое отклонение:
Ответ:
Пример 10. Решение: т.к. случайная величина 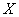
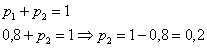
По определению математического ожидания: 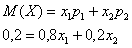
По формуле вычисления дисперсии: 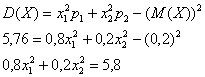
Составим и решим систему: 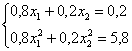
Умножим оба уравнения на 5: 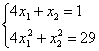
Из первого уравнения выразим: 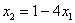
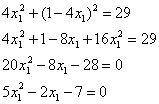
Решим полученное квадратное уравнение: 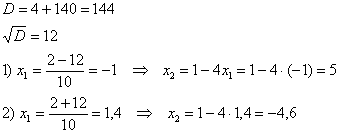
Условию 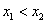
Ответ:
Проверка:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5