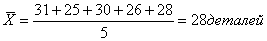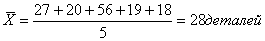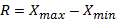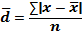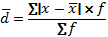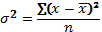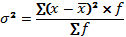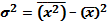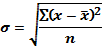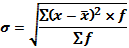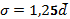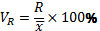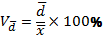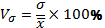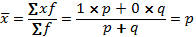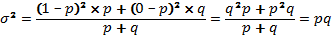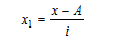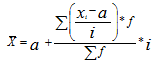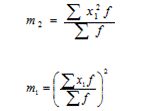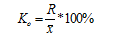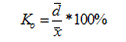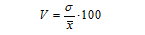Что показывает коэффициент осцилляции

Что показывает коэффициент осцилляции

— область применения и методику расчёта степенных средних величин;

— исчислять степенные средние величины;

— формулировать вывод по полученным результатам.

Наряду со средними величинами в статистике исчисляются показатели вариации. Вариацией в статистике называются различия индивидуальных значений изучаемого признака. Возникает вариация в силу того, что отдельные значения признака статистической совокупности формируются под воздействием разнообразных факторов. Значение изучения вариации в том, что по колеблемости признаков можно судить о качественной однородности совокупности. Совокупности могут иметь одинаковые значения средней величины, но отличаться колеблемостью индивидуальных значений.

Например : По имеющимся данным о дневной выработке рабочих двух бригад определить среднюю выработку рабочего за день в каждой бригаде, сделать вывод об однородности рассматриваемых совокупностей и надёжности их средних.

Выработка в первой бригаде: 31, 25, 30, 26, 28 деталей.

Выработка во второй бригаде: 27, 20, 56, 19, 18 деталей.

Исходные данные не сгруппированы, поэтому для расчёта средней выработки применяем среднюю арифметическую простую. Средняя дневная выработка рабочего:

в первой бригаде

во второй бригаде

Среднедневная выработка рабочего в обеих бригадах одинакова, но индивидуальные значения выработки во второй бригаде подвержены значительным колебаниям. Это вызывает необходимость измерять вариацию.

К абсолютным показателям вариации относятся

размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.

В нашем примере размах вариации индивидуальной выработки:

в первой бригаде R₁ =31-25=6 деталей

во второй бригаде R₂ =56-18=38 деталей

Сравнение этих показателей свидетельствует о том, что размах вариации индивидуальной выработки во второй бригаде на 32 детали больше, чем в первой бригаде. Однако размах вариации не улавливает колеблемости вариантов внутри изучаемой совокупности. Для получения обобщающей характеристики колеблемости всех вариантов совокупности исчисляются другие показатели вариации.

Среднее линейное отклонение даёт обобщённую характеристику степени колеблемости признака в совокупности относительно среднего уровня признака и рассчитывается как средняя арифметическая из индивидуальных линейных отклонений по формуле:

— для невзвешенных данных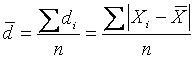

— для взвешенных данных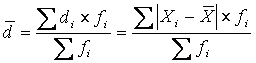

Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируют состав работающих, ритмичность производства, равномерность поставок материалов; разрабатывают системы материального стимулирования. Но этот показатель усложняет расчёты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.

В статистике дисперсия, центральный момент второго порядка, является оценкой одноимённого показателя теории вероятностей и оценкой дисперсии в математической статистике, что позволяет использовать теоретические положения этих дисциплин для анализа социально – экономических процессов. На дисперсии практически основаны все метод математической статистики. Большое значение имеет правило сложения дисперсий. Дисперсия рассчитывается как средний квадрат отклонений индивидуальных значений признака от среднего

значения признака по формуле:

— для невзвешенных данных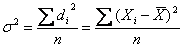

— для взвешенных данных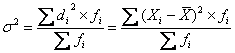

Для расчёта показателей вариации в нашем примере строим вспомогательную таблицу:

Индивидуальное линейное отклонение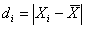

Источник

Тема 6 Показатели вариации

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления. Необходимо учитывать и разброс или вариацию значений отдельных единиц.

Основными показателями, характеризующими вариацию, являются: размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Размах вариации – простейший показатель, разность между максимальным и минимальным значениями признака.

\[ \begin R=x_-x_ \end \] Недостатком является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.

Дисперсия – средний квадрат отклонений значений признака от их средней величины и определяется по формулам простой

Если коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.

Показатели вариации могут быть использованы не только в анализе изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е.е в анализе взаимосвязей между показателями.

При проведении такого анализа совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным и результативным.

Для выявления взаимосвязи исходная совокупность делится на две или более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:

Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:

Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

\[ \begin \eta_э = \sqrt < \frac <\delta^2> <\sigma_o^2>> \end \] Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно p и q. Поэтому среднее значение альтернативного признака равно р. А дисперсия альтернативного признака равна pq. Дисперсия альтернативного признака равна произведению доли признака, обладающего характеристикой на долю признака, не обладающего характеристикой. Предельное значение дисперсии для альтернативного признака равно 0,25 при р=0,5.

Дисперсия альтернативного признака широко применяется в выборочном обследовании.

Изменения частот в вариационных рядах изменяются закономерно в связи с изменением варьирующего признака. Такие закономерности называются закономерностями распределения.

Основная задача анализа вариационных рядов заключается в выявлении подлинной закономерности распределения путем исключения влияния второстепенных, случайных для данного распределения факторов.

Если увеличить объем совокупности и уменьшить интервал в группах, то графическое изображение приближается к некоторой плавной кривой, которая называется кривой распределения.

Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.

Теоретическая кривая распределения – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для него факторов.

Выяснение общего характера распределения предполагает оценку его однородности, а также расчет показателей асимметрии и эксцесса.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии:

Его величина может быть положительной (для правосторонней асимметрии) и отрицательной (для левосторонней асимметрии).

Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Если асимметрия меньше 0,25, она считается незначительной.

Если коэффициент асимметрии находится в интервале от 0,25 до 0,5, то наличие асимметрии в генеральной совокупности проверяется с помощью определения оценки существенности на основе средней квадратической ошибки:

Для симметричных распределений может быть рассчитан показатель эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление. Показатель эксцесса определяется на основе центрального момента четвертого порядка по формуле:

Если показатель эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным. Среднеквадратическая ошибка эксцесса показывает, насколько существенен скачок в явлении и рассчитывается по формуле:

\[ \begin \sigma_ = \sqrt < \frac<24n(n-2)(n-3)> <(n-1)^2(n+3)(n+5)>> \end \] К структурным характеристикам ряда распределения относятся мода, медиана, квартили, децили и перцентили.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль первого порядка (нижний квартиль) и квартиль третьего порядка (верхний квартиль). Каждый из них отсекает соответственно ¼ и ¾ совокупности. Для расчета квартилей используются следующие формулы:

Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль отсекает 1/10 часть совокупности, а девятый дециль отсекает 9/10 частей. Рассчитываются децили по аналогичным формулам:

Перцентили – варианты, которые делят ранжированную совокупность на 100 частей.

Источник

Что показывает коэффициент осцилляции

Тема 1.8 Показатели вариации в статистике

1. Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Значения количественных признаков у отдельных единиц совокупности не постоянны, более или менее различаются между собой. Такое различие в величине признака носит название вариации. Таким образом, вариация имеет объективный характер и помогает познать сущность изучаемого явления.

2. Вариация – различия индивидуальных значений признака у отдельных единиц совокупности по состоянию за один и тот же интервал времени или же на один и тот же момент времени. Отдельные числовые значения признака, встречающиеся в изучаемой совокупности, называют вариантами значений. Наличие вариац ии у о тдельных единиц совокупности обусловлено влиянием большого числа факторов на формирование уровня признака. Изучение характера и степени вариации признаков у отдельных единиц совокупности является важнейшим вопросом всякого статистического исследования. Для описания меры изменчивости признаков используют показатели вариации.

3. Для измерения вариации признака применяются различные абсолютные и относительные показатели К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия и среднее квадратическое отклонение.

6. В экономико-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадратического отклонения. Среднее квадратическое отклонение рассчитывается как корень квадратный из дисперсии. Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражаются в тех же единицах измерения, что и варианты.

9. Для оценки точности расчетов по вариационному ряду можно применить правило сложения дисперсий. Общая дисперсия равна сумме межгрупповой и внутри групповой дисперсий. Чем меньше величина внутригрупповой дисперсии, чем ближе середины интервалов переменной Х к величинам групповых средних, тем точнее расчеты по вариационному ряду, тем они ближе к результатам расчетов по несгруппированным данным. Особенно это следует принимать во внимание при расчете дисперсии. Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Межгрупповая дисперсия характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под действием признака-фактора, положенного в основание группировки. Внутри групповая дисперсия отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора.

Источник

Показатели вариации

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ

2. Вариация альтернативного признака

3. Виды дисперсий. Правило сложения дисперсий

4. Правило сложения дисперсий для альтернативного признака

Зарегистрированные в процессе статистического наблюдения различия величины признака уотдельных единиц совокупности называются вариацией признака. По степенивариации признака можно судить о процессах развития изучаемых явлений, о типичности средних величин. Дело в том, что средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывая строения совокупности.

Для определения меры вариации признака в статистике исполь­зуются абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадрата чес кое отклонение.

Размах вариации (R) является самым простым из абсолютных показателей вариации и представляет собой разность между максимальным и минимальным значениями признака:

Величина размаха вариации зависит только от крайних значений учитывает всех изменений варьирующего признака в пределах изучаемой совокупности. Поэтому при изучении вариации нельзя ограничиваться расчетом только этого показателя. Для анализа вариации необходимы показатели, дающие обобщенную характер всех колебаний варьирующего признака.

Среднее линейное отклонение является простейшим показате­лем такого типа и представляет собой среднюю величину абсолютных отклонений индивидуальных значений признака от их средней ариф­метической величины.

Среднее линейное отклонение для несгруппированных дан­ных определяется по формуле (5.2):

Среднее линейное отклонение для сгруппированных данных рассчитывается так (5.3):

Дисперсия для несгруппированных данных вычисляется по формуле (5.4):

Дисперсия для сгруппированных данных рассчитывается так (5.5):

Для расчета дисперсии применяется также следующая формула (5.6):

Среднее квадратическое отклонение представляет собой ко­рень квадратный из дисперсии (5.7) или (5.8):

Среднее квадратическое отклонение также как и среднее линейное отклонение показывает, на сколько в среднем отличаются индивидуальные значения признака от их среднего значения. Однако величине среднеквадратическое отклонение во всех случаях превыша­ет среднее линейное, так как более чутко реагирует на вариацию. Для симметричных и умеренно асимметричных распределений имеет ме­сто следующее соотношение (5.9):

Размах вариации, среднее линейное отклонение и среднееквад­ратическое отклонение выражаются в именованных числах, т. е. име­ют единицу измерения (такую же, как и значения признака). Поэтому их нельзя непосредственно использовать для сравнения степени ва­риации по одному и тому же признаку в двух группах с разным уров­нем средних, а также для сравнения вариации двух различных призна­ков в одной группе. В этих случаях применяются следующие относи­тельные показатели вариации.

Коэффициент осцилляции (5.10)

Относительное линейное отклонение (линейный коэффициент вариации) (5.11):

Коэффициент вариация (5.12):

Коэффициент вариации позволяет не только получить обоб­щающую характеристику вариации признака в совокупности, но и дает возможность сделать выводы об однородности совокупности.Со­вокупность считается однородной, если коэффициент вариации не превышает 33%.Средние величины, рассчитанные по однородной совокупности, являются ее достаточно надежными характеристиками.

Вариация альтернативного признака

В статистике помимо показателей вариации количественных признаков широко используются показатели вариации качественных признаков (в частности, при проектировании выборочного наблюдения). Вариация альтернативного признака количественно проявляется в значении 0 (нуля) у единиц, которые этим признаком не обладают, или 1 (единицы) у тех, которые данный признак имеют. Пусть р — до­ля единиц в совокупности, обладающих данным признаком, q — доля единиц, не обладающих данным признаком, причем p + q = 1.

Среднее значение альтернативного признака определим по формуле средней арифметической (5.13):

Дисперсия альтернативного признака определяется по формуле (5.14):

Таким образом, средняя величина альтернативного признака равна его доле в данной совокупности, а дисперсия — произведению доли его наличия и доли его отсутствия. Максимальное значение дис­персии альтернативного признака, означающее максимальную неод­нородность совокупности, равно 0,25 при p = q = 0,5.

Источник

Абсолютные и относительные показатели вариации

Вариация – различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

К показателям вариации относятся:

I группа — абсолютные показатели вариации

· среднее линейное отклонение

· среднее квадратическое отклонение

II группа — относительные показатели вариации

· относительное линейное отклонение

Среднее линейное отклонение — средняя арифметическая абсолютных значений отклонений (модуль отклонений) отдельных вариантов от их средней арифметической:

1. для несгруппированных данных (простое)

2. для сгруппированных данных (взвешенное)

Дисперсияпризнака — средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия для несгруппированных данных

2. Взвешенная дисперсия для вариационного ряда

Cвойства дисперсии:

1. если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится;

2. если все значения признака уменьшить или увеличить в одно и то же число раз (kраз), то дисперсия уменьшится или увеличится в k 2 раз.

Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

где i – величина интервала, X₁ — новые (преобразованные) значения вариантов (А – условное начало, в качестве которого удобно использовать середину интервала или величину признака, обладающего наибольшей частотой.

1. Момент второго порядка

2. Квадрат момента первого порядка

Среднее квадратическое отклонениеравно корню квадратному из дисперсии:

1. для несгруппированных данных (простое)

2. для вариационного ряда по сгруппированным данным (взвешенное)

Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются отдельные варианты от ихсреднего значения.

Среднее значение альтернативного признака и его дисперсия:

1. Среднее значение альтернативного признака

2. Дисперсия альтернативного признака

3. 1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг общей средней.

4.

5. 2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.

6.

8.

Источник