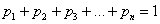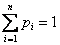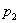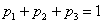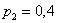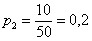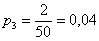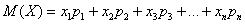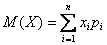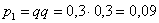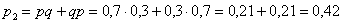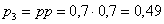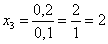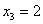Что показывает математическое ожидание случайной величины и как найти математическое ожидание дсв

Математическое ожидание

Математическое ожидание — это ожидаемый результат от какого-то действия.

Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.

Случайная величина может быть двух типов:

Математическое ожидание дискретной случайной величины рассчитывается этой формулой:

Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет «1» — 1/6, «2» — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).

Для непрерывной случайной величины используется эта формула:

В этом случае рассчитывается интеграл в заданном интервале.

Примеры вычисления математического ожидания

Пример 1

Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:

Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2

Пример 2

Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.

Используется формула для непрерывной случайной величины:

Пример 3

Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:

Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6

Пример 4

Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.

Используется формула для непрерывной случайной величины:

Источник

Дискретные случайные величины

Дискретная случайная величина — это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать.

Пример 1. Приведем примеры дискретных случайных величин:

в) число прибывших кораблей на борт (счетное множество значений).

г) число вызовов, поступающих на АТС (счетное множество значений).

1. Закон распределения вероятностей дискретной случайной величины.

$\begin<|c|c|>
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end$

$\begin<|c|c|>
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end$

2. Математическое ожидание дискретной случайной величины.

3. Дисперсия дискретной случайной величины.

Возможные значения случайных величин с равными математическими ожиданиями могут по-разному рассеиваться вокруг своих средних значений. Например, в двух студенческих группах средний балл за экзамен по теории вероятностей оказался равным 4, но в одной группе все оказались хорошистами, а в другой группе — только троечники и отличники. Поэтому возникает необходимость в такой числовой характеристике случайной величины, которая бы показывала разброс значений случайной величины вокруг своего математического ожидания. Такой характеристикой является дисперсия.

4. Функция распределения дискретной случайной величины.

Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.

Источник

Математическое ожидание ДСВ и его свойства

Пусть дана случайная величина Х:

Опр. Математическое ожидание дискретной случайной величины X равно сумме произведений значений случайной величины на соответствующие им вероятности:

(1)

Предположим, что подбрасывают монету. Если выпадет герб, выигрывают одно очко, если цифра, — проигрывают одно очко. Чему равен ожидаемый выигрыш? Интуитивно понятно, что шансы выиграть и проиграть одну и ту же сумму очков равны, и, следовательно, в среднем ожидаемый выигрыш будет равен нулю, Выигрыш в этой игре — случайная величина; можно вычислить ожидаемое значение, используя формулу (1):

М(Х)= 1 • 1/2 + (-1) • 1/2 = 0.

Поэтому математическое ожидание называют средним значением. Причина такого названия состоит в том, что среднее значение случайной величины есть оценка, которую ожидают получить.

Свойства математического ожидания ДСВ

1. Математическое ожидание постоянной величины равно этой постоянной:

2. Постоянный множитель можно выносить за знак математического ожидания:

гдеС — постоянная.

3. Математическое ожидание алгебраической суммы конечного числа п случайных величин равно алгебраической сумме их математических ожиданий:

4. Математическое ожидание произведения конечного числа п независимых случайных величин равно произведении 1 их математических ожиданий:

5. Если все значения случайной величины X уменьшить (увеличить) на одно и то же число с, то ее математическое ожидание уменьшится (увеличится) на то же число с:

Следствие. Математическое ожидание отклонения значе­ний случайной величины X от ее математического ожида­ния равно нулю:

Дисперсия ДСВ и ее свойства

Для практических нужд бывает очень важно знать, как группируются значения случайных величины около ее математического ожидания.

1) при стрельбе из орудия важно, чтобы снаряды ложились кучнее;

2) при измерении какой-то величины важно, чтобы ошибки измерения как можно меньше отличались от их среднего значения.

Задача: Найти мат. ожидание случайной величины Х и У, которые заданы следующими распределениями:

Математическое ожидание ничего не говорит о том, как рассеяны значения случайной величины вокруг его среднего значения (0). Рассеяние случайной величины характеризуетсядисперсией.

Опр. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

Теорема: Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания данной случайной величины

Задача. Число очков, выбиваемых при одном выстреле любого из двух стрелков, подчиняется следующим законам распределения

Кто стреляет лучше?

Так как речь идет о рассеянности, то нужно найти дисперсию

М(Х1) = 1 0,3 + 2 0,2 + 3 0,5 = 2,2

М(Х2) = 1 0,1 + 2 0,6 + 3 0,3 = 2,2

М(Х1 2 ) = 1 0,3 + 4 0,2 + 9 0,5 = 5,6

М(Х2 2 ) = 1 0,1 + 4 0,6 + 9 0,3 = 5,2

Ответ: лучше стреляет второй стрелок.

Свойства дисперсий

Д(СХ) = М(СХ – М(СХ)) 2 = М(СХ – СМ(Х)) 2 = М(С(Х – М(Х))) 2 =

С 2 М(Х – М(Х)) 2 = С 2 Д(Х)

где Х₁, Х₂, … Х_n – взаимно-незасвисимые величины.

Постоянная не дает рассеяние ее прибавление к случайной величине Х ведет лишь к смещению всех ее значений на одну и ту же постоянную величину, а рассеяние остается прежним.

Источник

Случайные величины. Дискретная случайная величина.
Математическое ожидание

Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:

Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.

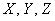
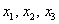
Случайные величины, как правило, обозначают через *, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .

* Иногда используют 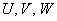, а также греческие буквы

Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:

– количество очков, которое выпадет после броска игрального кубика.

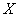
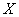
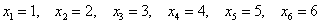
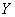
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина может принять одно из следующий значений:

.

– количество мальчиков среди 10 новорождённых.

Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:

, либо мальчиков – один и только один из перечисленных вариантов.

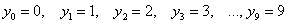
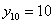
И, дабы соблюсти форму, немного физкультуры:

– дальность прыжка в длину (в некоторых единицах).

Её не в состоянии предугадать даже мастер спорта 🙂

Тем не менее, ваши гипотезы?

Коль скоро речь идёт о множестве действительных чисел, то случайная величина 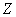может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.

Таким образом, случайные величины целесообразно разделить на 2 большие группы:

1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.

…нарисовались непонятные термины? Срочно повторяем основы алгебры!

2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.

Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ

Сначала разберём дискретную случайную величину, затем – непрерывную.

Закон распределения дискретной случайной величины

– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:

Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».

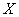
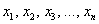
А теперь очень важный момент: поскольку случайная величина обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

или, если записать свёрнуто:

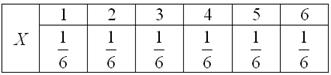
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:

Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:

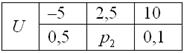
Некоторая игра имеет следующий закон распределения выигрыша:

Найти

…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.

Решение: так как случайная величина 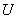может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

Разоблачаем «партизана»: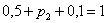

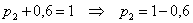
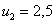
– таким образом, вероятность выигрыша условных единиц составляет 0,4.

Контроль: 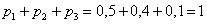, в чём и требовалось убедиться.

Ответ:

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:

В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 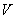– размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 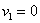рублей.

Всего таковых билетов 50 – 12 = 38, и по классическому определению:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

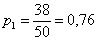
С остальными случаями всё просто. Вероятность выигрыша 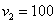рублей составляет:

И для :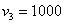

Проверка: 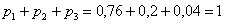– и это особенно приятный момент таких заданий!

Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

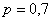
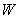
Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.

…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.

Математическое ожидание дискретной случайной величины

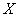
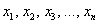
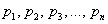
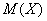
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

или в свёрнутом виде:

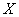
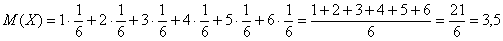
Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:

очка

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

Теперь вспомним нашу гипотетическую игру:

Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:

, таким образом, математическое ожидание данной игры проигрышно.

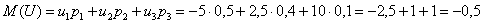
Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 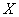– его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?

Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

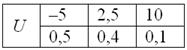
Случайная величина 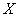задана своим законом распределения вероятностей:

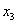
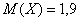
Найти , если известно, что . Выполнить проверку.

Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.

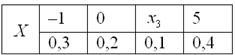
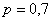
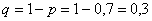
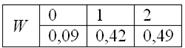
Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда:
– вероятность промаха.

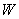
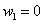
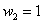
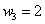
Составим – закон распределения попаданий при двух выстрелах:

– ни одного попадания. По теореме умножения вероятностей независимых событий:

– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:

– два попадания. По теореме умножения вероятностей независимых событий:

Проверка: 0,09 + 0,42 + 0,49 = 1

Ответ:

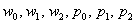
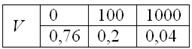
Примечание: можно было использовать обозначения – это не принципиально.

Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: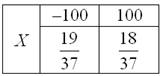

Вычислим математическое ожидание: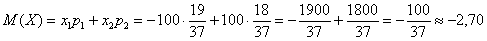

Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания: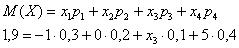

поменяем части местами и проведём упрощения: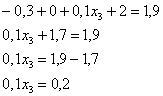

таким образом:

Выполним проверку: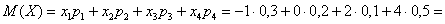

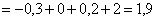
, что и требовалось проверить.

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник