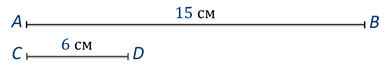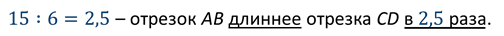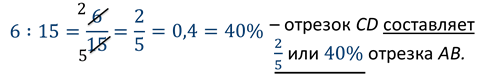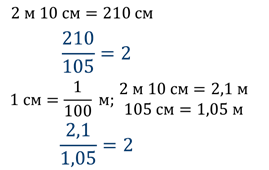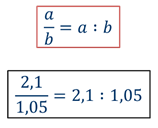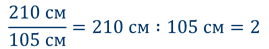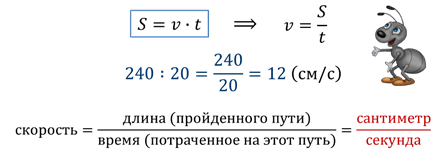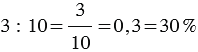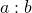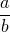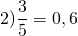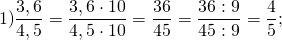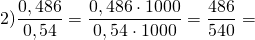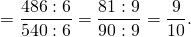Что показывает отношение двух чисел 6 класс

Отношения

Урок 20. Математика 6 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Отношения»

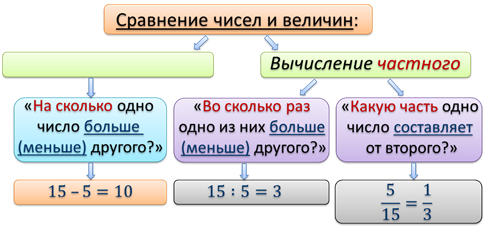
Для решения практических задач человеку часто приходится сравнивать разные значения одной и той же величины – массы, расстояния, времени, скорости, стоимости, объёма, площади и т.д.

Для сравнения чисел и величин существуют, как вы знаете, два способа:

1-ый: вычисление разности и 2-ой: вычисление частного.

Оба этих способа используют часто при решении практических задач, но служат они для разных целей. К делению прибегают в тех случаях, когда хотят получить качественную оценку или относительную оценку той или иной ситуации.

На экране изображены два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?

Вторая задача: на экране изображены эти же два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Но поставим вопрос по-другому: какую часть отрезок CD составляет от отрезка АВ?

Обе рассмотренные задачи решаются делением, и ответ даётся в виде частного. В таких случаях частное двух чисел называют их отношением.

Частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

Иными словами, отношение двух чисел – это другое название их частного. Отношение чисел записывают с помощью знака деления, а также с помощью черты обыкновенной дроби.

Частные чисел читают так:

Напомним, что отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого.

Черта дроби используется для записи отношения и тогда, когда его члены не являются натуральными числами.

Рост дяди Степы 2 м 10 см, а рост мальчика Васи – 105 см. Во сколько раз дядя степа выше мальчика Васи?

Но ведь дробную черту мы использовали для записи дробей! А сейчас записана не дробь. Верно. Но вы давно знаете, что при записи деления натуральных чисел вместо знака деления можно использовать дробную черту. Так вот, договариваются о том же и при записи деления любых чисел.

Итак, если а и b – любые числа, то

Сделаем важное замечание:

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.

Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина.

Вот, например, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи.

Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом.

А теперь давайте разберёмся, почему отношение разноимённых величин – это новая величина.

Муравей за 20 секунд пробегает 240 сантиметров. Определите скорость движения муравья.

Отметим, что обозначения км/ч, м/с и т.п. приняты именно потому, что расстояние делят на время. Их обычно записывают с наклонной чертой.

В виде отношений определяются и другие величины:

Из основного свойства частного следует свойство отношения.

Давайте вспомним основное свойство частного:

если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Следовательно, получаем свойство отношения:

отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Мы с вами убедились, что свойство отношения действует. Мы умножили числитель и знаменатель дроби на одно и то же число, само же отношение не изменилось.

Итак, сегодня на уроке мы узнали, что частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

И свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Источник

Что такое отношение двух чисел: определение, запись, примеры

В данной публикации мы рассмотрим, что такое отношение двух чисел, как записывается, а также, какие действия с ним можно выполнять, чтобы оно осталось неизменным. Представленная информация сопровождается практическими примерами.

Определение отношения чисел

Отношением двух чисел называется их частное, т.е. деление одного на другое.

Например, отношение 24 к 6 можно записать как или представить в виде обыкновенной дроби. В этом случае в знаменателе пишется число, с которым выполняется сравнение, а в числителе – то, которое сравнивается:

Примечание: вместо предлога “к” иногда используется “по сравнению с”.

С помощью отношения чисел показывается:

1. Во сколько раз одно из них больше другого (когда делимое больше делителя).

То есть 14 в два раза больше 7.

2. Какую часть одно число занимает в другом (делитель больше делимого).

То есть 5 составляет одну четвертую часть от числа 20 (или 25%).

Умножение/деление отношения на число

Если умножить или разделить оба элемента отношения на одно и то же число, отличное от нуля, в результате получится новое отношение, которое равно исходному.

Примечание: Это есть не что иное как основное свойство дроби.

Источник

Отношения

Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.

Частное двух чисел и , отличных от нуля, называют отношением чисел и , или отношением числа к числу .

Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.

— отношение числа к числу ;

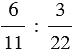
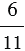
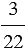
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .

Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .

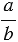
Основное свойство отношения:

Запишем отношение числа 3 к числу 10 и найдем его значение:

То есть отношение двух чисел можно выразить в процентах.

Процентное отношение показывает, сколько процентов одно число составляет от другого.

Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Пример:

Сколько процентов составляет число 5 от числа 10?

Ответ: 50% составляет число 5 от числа 10.

Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.

Например:

Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.

Отношение длины прямоугольника к его ширине равно 12 : 100 = .

Отношение ширины прямоугольника к его длине равно 100 : 12 = .

Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.

Пусть на карте задан масштаб 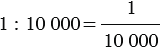, то есть карта сделана в масштабе одна десятитысячная.

Найдем, какой длине на местности соответствует отрезок 5 см на карте.

Для решения обозначим через длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:

5 : = 1 : 10 000;

Решаем данное уравнение:

= 510 000;

= 50 000;

50 000 см = 500 м = 0,5 км.

Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.

Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.

Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:

: 9,5 = 1 : 10 000;

Решаем данное уравнение:

= 9,5 : 10 000;

= 0,00095;

0,00095 км = 0,95 м = 95 см.

Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.

Поделись с друзьями в социальных сетях:

Источник

20. Отношения

Задача 1. От куска материи длиной 5 м отрезали 2 м. Какую часть куска материи отрезали?

Если значения двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин (отношением длин, отношением масс, отношением площадей и т. д.).

Задача 2. Длина железной дороги 360 км. Электрифицировано 240 км этой дороги. Какая часть дороги электрифицирована? Во сколько раз вся дорога длиннее её электрифицированной части?

Р е ш е н и е. Чтобы найти, какая часть дороги электрифицирована, берём отношение 240 : 360. Записываем это отношение в виде дроби и сокращаем её на 120. Получим Значит, электрифицировано всей дороги.

Чтобы узнать, во сколько раз вся дорога длиннее своей электрифицированной части, берём отношение 360 : 240. Записываем его в виде дроби и сокращаем эту дробь на 120. Получим Значит, вся дорога в 1,5 раза длиннее её электрифицированной части.

Числа взаимно обратны, поэтому и отношения 2 к 3 и 3 к 2 также называют взаимно обратными.

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

Задача 3. Масса станка 9,6 ц, а масса электромотора 36 кг. Найдите отношение массы электромотора к массе станка.

Р е ш е н и е. Выразим массу станка в килограммах. Получим 9,6 ц = 960 кг. Значит, отношение массы электромотора к массе станка равно

Итак, масса электромотора составляет 0,0375 массы станка.

Этот ответ можно выразить в процентах: 0,0375 = 3,75 %. Значит, масса электромотора составляет 3,75% массы станка.

Что называют отношением двух чисел?
Что показывает отношение двух чисел?
Как узнать, какую часть число а составляет от числа b?
Как узнать, сколько процентов одно число составляет от другого?

722. Найдите отношение:

723. Проволока разрезана на два куска. Первый кусок имеет длину 9 м, а второй — 14,4 м. Найдите, какую часть всей проволоки составляет первый кусок; второй кусок. Какую часть длина первого куска составляет от длины второго куска?

724. Внутри угла АОС проведён луч ОВ так, что ∠AOB = 56° и ∠BOC = 40°. Какую часть угла АОС составляет угол ЛОВ; угол ВОС? Выполните построение этих углов с помощью транспортира.

Источник

Что такое отношение чисел

Здесь мы обсудим, что такое отношение чисел и что показывает отношение двух чисел.

Отношение чисел можно записать двумя способами: с помощью знака деления либо с помощью дроби:

Читают: «отношение a к b».

Числа a и b называют членами отношения.

a — предыдущий член отношения, b — последующий член отношения. a и b должны быть отличны от нуля.

2. Отношения используют для сравнения двух величин.

Примеры отношения чисел:

Отношение 120:3 показывает, что 120 в сорок раз больше 3.

Отношение 3/5 показывает, что 3 составляет 0,6 от 5.

3. Основное свойство отношения:

Отношение не изменится, если его члены умножить или разделить на одно и то же число, отличное от нуля.

(основное свойство отношения вытекает из основного свойства дроби ).

Таким образом, отношение дробных чисел можно заменить отношением целых чисел.

4. Примеры отношения величин.

— скорость (отношение пройденного пути ко времени, за которое путь был пройден);

— производительность труда (отношение объема работы ко времени, за которое выполняется работа);

— цена ( отношение стоимости товара к количеству единиц);

— масштаб (отношение длины отрезка на карте к расстоянию между соответствующими точками на местности);

— урожайность (отношение массы собранного урожая к общей площади полей, с которой был собран урожай).

Далее мы рассмотрим равенство двух отношений и его практическое применение.

11 Comments

Ужс…по таким темам у меня 6 классе колы по кд-шкам.

Видимо, я слишком тупа для этой темы >. Светлана Иванова 23.08.2017 06:21 Ответить

Не так много людей, которые понимают тему с первого раза. Попробуйте вернуться к ней еще пару раз, и прояснится.

Добрый вечер,
У вас там описка в первом примере : 4/5
Нет?
С уважением

Да, была опечатка. Спасибо, Марк!

Я это понял сразу (после пары подзатыльников от отца)!! Подача отличная, в 6 кл просто изи учиться!!

мне не суждено понимать

Не святые горшки обжигают. Понять математику не так уж и сложно, было бы желание и трудолюбие.

А как из отношения число сделать?

Разделить первое число на другое. Например, 6:5=1,2.

Источник