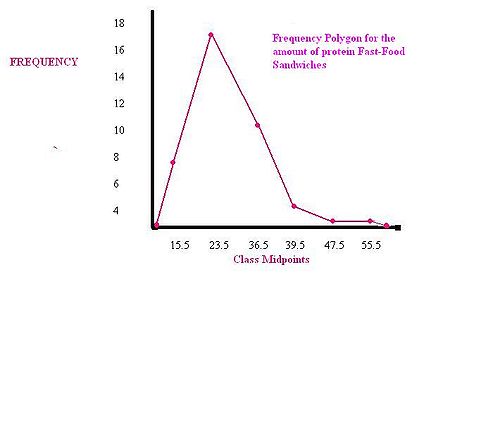
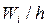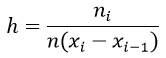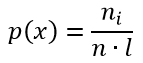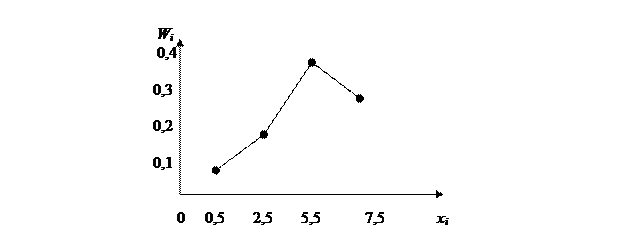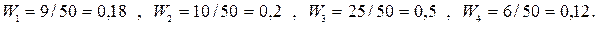Что показывает полигон частот
Постройка полигона и гистограммы частот
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
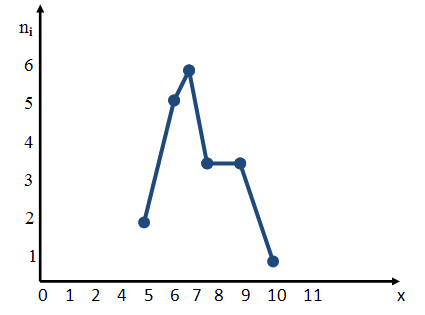
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2). (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
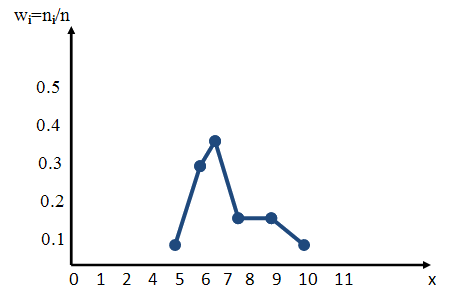
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2). (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
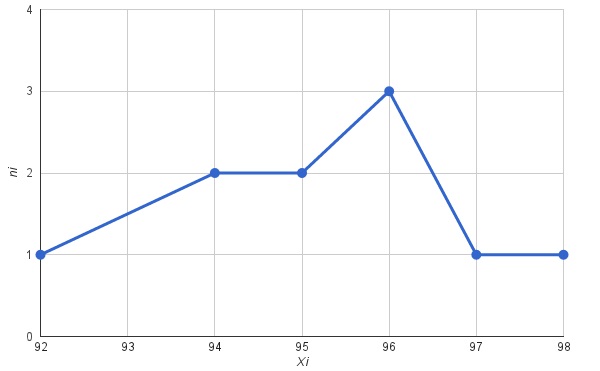
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
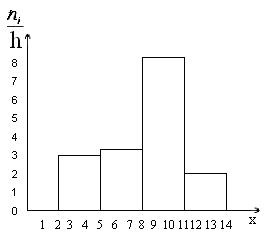
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Полигон частот
Полиго́н часто́т (в математической статистике) — один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.
Ссылки
См. также
Полезное
Смотреть что такое «Полигон частот» в других словарях:
Полигон (значения) — Полигон: Полигон участок суши или моря, который предназначен для испытаний различных видов техники. Военный полигон объект для проведения войсковых учений или испытаний вооружений и военной техники. Полигон оборудованная территория,… … Википедия
полигон — 3.30 полигон: Испытательное средство и средство обучения персонала заказчика. Обеспечивает создание готовой к внедрению и предварительно проверенной (в условиях полигона) АСУТП или ее компонентов. Полигон АСУТП, оснащенный специальными средствами … Словарь-справочник терминов нормативно-технической документации
полигон кумулятивных частот — 2.19. полигон кумулятивных частот Ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам классов, а ординаты либо кумулятивным абсолютным частотам, либо кумулятивным относительным частотам Источник: ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации
ПОЛИГОН — – ломаная линия, соединяющая точки, соответствующие величинам частот, откладываемых по осям ординат [2, c. 67; 16, c.46; 89, c. 175] … Современный образовательный процесс: основные понятия и термины
ЧАСТОТ ПОЛИГОН — Способ рисуночного представления плотности распределения. Частота каждого интервала класса (см. групповая плотность распределения) откладывается на графике, и проводится линия, соединяющая эти точки. Эта линия называется гистограммой … Толковый словарь по психологии
РАСПРЕДЕЛЕНИЯ ПОЛИГОН — график распределения частот для порядковых и количественных переменных ( также Шкала измерительная). Представляет собой ломаную линию, наглядно демонстрирующую распределение частот. Линия Р.П. соединяет точки, координаты которых для дискретных и… … Социология: Энциклопедия
РАСПРЕДЕЛЕНИЕ ЧАСТОТЫ — Любое распределение, основанное на перечислении частоты встречаемости значений, согласно классам или категориям. Таким образом, каждому набору классов присваивается номер, который представляет наблюдаемую частоту. Независимо от метода… … Толковый словарь по психологии
НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ СТАТИСТИКИ — методы математич. статистики, не предполагающие знания функционального вида генеральных распределений. Название непараметрические методы подчеркивает их отличие от классических параметрических методов, в к рых предполагается, что генеральное… … Математическая энциклопедия
Гистограмма — Пример гистограммы У этого термина существуют и другие значения, см. Гистограмма (значения). Гистограмма (от др. греч … Википедия
КРИВАЯ РАСПРЕДЕЛЕНИЯ — – это предел, к которому стремится полигон частот при неограниченном увеличении объема статистической совокупности и уменьшения интервалов (увеличение точности измерения, переход от дискретной величины к непрерывной) [73, c. 16; 89, c. 178] … Современный образовательный процесс: основные понятия и термины
Гистограмма относительных частот
Что такое полигон относительных частот
Схематическое изображение статистического ряда распределения может быть представлено полигоном и гистограммой частот. Также выделяют понятия полигон относительных частот и гистограмма относительных частот
Полигон относительных частот – это ломаная, состоящая из отрезков, соединяющих точки с координатами (xi, ωi).
Построение полигона частот
Алгоритм составления полигона относительных частот: на оси OX отмечают варианты xi, на оси OY откладывают значения ωi. Затем точки с координатами (xi, ωi) соединяют прямыми отрезками. Ломаная, образованная в результате, является полигоном относительных частот.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пример
Полигон частот для ряда распределения:
Гистограмма относительных частот, описание
Гистограмма относительных частот – это фигура ступенчатого вида, в составе которой имеются прямоугольники. Основанием этих прямоугольников являются частичные интервалы длиною h, а высотами служит плотность относительной частоты – величина, определяемая с помощью отношения ωi/h.
Строить гистограмму следует, соблюдая следующий порядок. На оси абсцисс указывают частичные интервалы. Над ними на расстоянии, равном плотности относительной частоты (ωi/h), отмечают отрезки, параллельные оси OX.
Пример
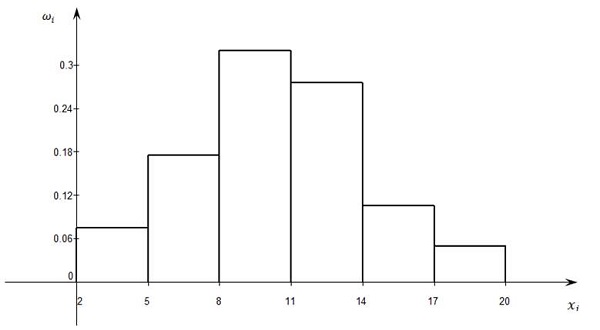
Интервалы, xi: 2–5, 5–8, 8–11, 11–14, 14–17, 17–20.
Частота вариант, ni: 15, 35, 64, 55, 21, 10 (всего 200).
Относительные частоты, ωi: 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (всего 1,000).
Гистограмма данного ряда распределения имеет вид:
Площадь прямоугольников гистограммы
Площадь одного прямоугольника, входящего в состав гистограммы относительных частот, равна относительной частоте вариант и вычисляется по формуле:
Для вычисления площади всей гистограммы необходимо сложить площади всех прямоугольников, составляющих ступенчатую фигуру. Следовательно, искомая величина будет равна единице.
Примеры решения задач
Задача 1
Постройте полигон относительных частот для следующего вариационного ряда:
ni: 15, 35, 64, 55, 21, 10.
Решение
Для начала необходимо вычислить относительные частоты:
ni: 15, 35, 64, 55, 21, 10 (итого 200).
ωi: 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (итого 1,000).
Построим искомую ломаную:
Задача 2
Построить гистограмму относительных частот распределения, имея следующие данные:
Частичный интервал при длине h, равной 3: 2–5, 5–8, 8–11, 11–14.
Решение
Сначала определим относительные частоты. Для этого установим объем выборочной совокупности n:
Далее вычислим ωi/h, то есть плотность частоты:
Образуются следующие данные:
Частичный интервал: 2–5, 5–8, 8–11, 11–14.
Сумма относительных частот: 0,18; 0,2; 0,5; 0,12.
Полигон и гистограмма
ni — частоты;
wi — относительные частоты;
n — объём выборки;
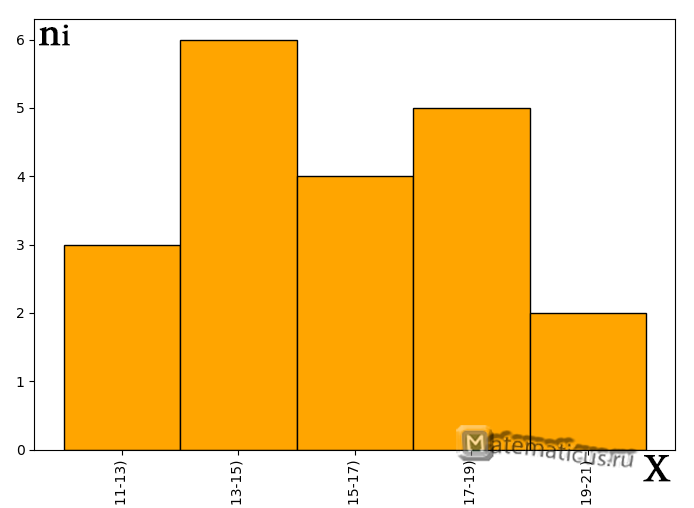
| Номер интервала | Абсолютная частота, ni | Частотный интервал |
| 1. | 3 | [11;13) |
| 2. | 6 | [13;15) |
| 3. | 4 | [15;17) |
| 4. | 5 | [17;19) |
| 5. | 2 | [19;21) |
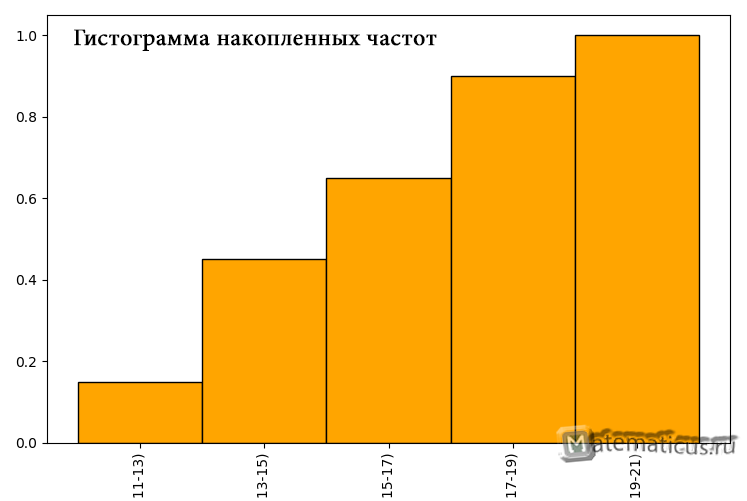
Таблица относительных частот и эмпирическая плотность распределения частоты
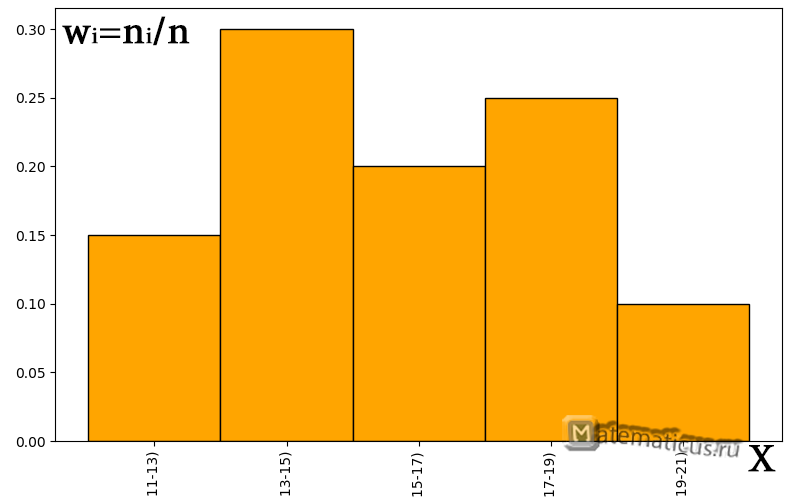
| Частотный интервал | Относительная частота, wi=ni/n | Эмпирическая плотность распределения частоты ni/ Δ |
| [11;13) | 0.15 | 1.5 |
| [13;15) | 0.3 | 3 |
| [15;17) | 0.2 | 2 |
| [17;19) | 0.25 | 0.25 |
| [19;21) | 0.1 | 0.1 |
График гистограммы абсолютных частот
График гистограммы относительных частот
Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им частоты ni и соединяют точки.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.7 / 5. Количество оценок: 11
Полигон и гистограмма



Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат wi. Точки (xi, wi) соединяют отрезками прямых и получают полигон относительных частот.
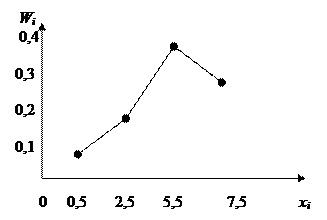
На рисунке изображен полигон относительных частот следующего распределения:
| x | 1,5 | 3,5 | 5,5 | 7,5 |
| w | 0,1 | 0,2 | 0,4 | 0,3 |
Рис. 6. Полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-ый интервал.
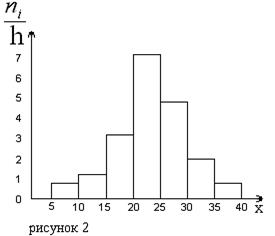
Рис. 7. Гистограмма частот.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии 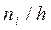
Площадь i-го частичного прямоугольника равна 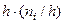
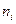
На рисунке 2 изображена гистограмма частот распределения объема n =100, приведенного в таблице 1.
| Частичный интервал, длиною h=5 | Сумма частот вариант частичного интервала 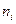 | Плотность частоты 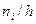 |
| 5 – 10 | 0,8 | |
| 10 – 15 | 1,2 | |
| 15 – 20 | 3,2 | |
| 20 – 25 | 7,2 | |
| 25 – 30 | 4,8 | |
| 30 – 35 | 2,0 | |
| 34 – 40 | 0,8 |
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии 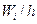
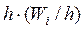
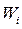
1. В результате выборки получена следующая таблица распределения частот.
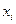 |
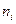 |
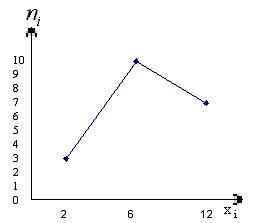
Построить полигоны частот и относительных частот распределения.
Для начала построим полигон частот.
Рис. 8. Полигон частот.
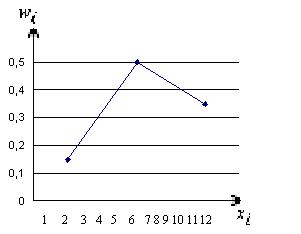
Чтобы построить полигон относительных частот найдем относительные частоты, для чего разделим частоты на объем выборки n.
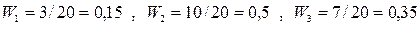
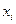 | |||
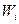 | 0,15 | 0,50 | 0,35 |
Построим полигон относительных частот.
Рис. 9. Полигон относительных частот.
2. Построить гистограммы частот и относительных частот распределения.
Найдем плотность частоты 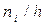
| Частичный интервал, длиною h = 3 | Сумма частот вариант частичного интервала 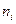 | Плотность частоты 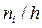 |
| 2 – 5 | ||
| 5 – 8 | 3,3 | |
| 8 – 11 | 8,3 | |
| 11 – 14 |
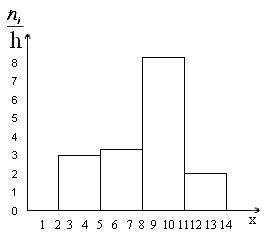
Построим гистограмму частот.
Рис. 10. Гистограмма частот.
Чтобы построить гистограмму относительных частот, нужно найти относительные частоты. Для этого найдем объем выборки n.
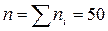
Теперь найдем относительные частоты 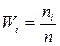
| Частичный интервал | Сумма относительных частот 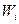 | Плотность частоты 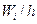 |
| 2 – 5 | 0,18 | 0,06 |
| 5 – 8 | 0,2 | 0,07 |
| 8 – 11 | 0,5 | 0,16 |
| 11 – 14 | 0,12 | 0,04 |
Плотности частот