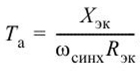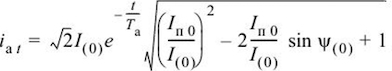Что показывает постоянная времени процесса затухания
Что показывает постоянная времени процесса затухания
При перебросе ключа К из положения 1 в положение 2 имеем
а при перебросе ключа К из положения 2 в положение 1
Анализируя полученные зависимости, можно установить, что
б) в моменты коммутации (скачкообразного подключения или отключения источника) имеют место всплески (броски) тока в цепи емкости, величина которых зависит от суммарного сопротивления, включенного последовательно с емкостью. Следовательно, токи в ветвях с емкостями в переходном режиме во много раз могут превышать установившиеся значения;
2. Анализ переходных процессов в цепи первого порядка с индуктивным элементом (схема рис.11.1,б)
Процессы изменения тока в индуктивности и напряжения на индуктивности при подключении ее через сопротивление R 2 к источнику напряжения протекает в соответствии с уравнениями
Для той же цепи) при перебросе ключа К из положения 2 в положение 1 уравнения, определяющие ток и напряжение на индуктивности, принимают вид
Графики полученных зависимостей приведены на рис. 12.2,а, б.
Анализ их показывает, что
а) при подключении индуктивности к источнику напряжения через сопротивление R 2 и замыкании ее на сопротивления R 1 и R 2 при отключенном источнике имеет место монотонный (экспоненциальный) процесс изменения тока через индуктивность;
Графики зависимостей представлены на рис.12.3,а.
Случай d = w 0 соответствует предельному случаю апериодического процесса в рассматриваемой цепи и носит название «критического случая». Малейшее уменьшение сопротивления R или увеличение индуктивности L приводит к изменению характера свободной составляющей процесса (она становится колебательной). В «критическом случае» переходный процесс по характеру не отличается от рассмотренного выше и кривые напряжения на емкости и тока в цепи, определяемые соотношениями
аналогичны соответствующим кривым, представленным на рис. 12.3,а.
Величину часто называют постоянной времени колебательного контура, поскольку за время ордината огибающей уменьшается (изменяется) в «e» раз.
Чем меньше δ по сравнению с ω 0 (чем меньше сопротивление R ), тем медленнее затухают колебания и тем ближе частота свободных колебаний ω св к резонансной частоте контура, определяемой соотношением
Относительное затухание колебаний характеризуется так называемым декрементом колебаний, представляющим отношение мгновенных значений тока через один период
Декремент (затухание) колебаний не зависит от времени, так как отношение амплитуд в любом месте кривой тока имеет одно и тоже значение.
Натуральный логарифм декремента (затухания) колебаний называется логарифмическим декрементом колебания
Оценка качества процессов регулирования
Оценка качества процессов регулирования
Система может быть устойчивой, т. е. ее переходный процесс носит затухающий характер, но время затухания настолько велико или ошибка в установившемся режиме настолько большая, что практически данная система не может быть использована. Поэтому система должна быть не только устойчивой, но и иметь определенный переходный процесс, а ее ошибки в установившихся режимах не должны превышать допустимых.
Для сравнительного анализа различных автоматических систем необходимо иметь некоторые числовые характеристики этих систем, позволяющие оценивать, какая из них будет более эффективной. Эти числовые характеристики и называются критериями качества.
Критерии качества позволяют дать количественную оценку различным автоматическим системам и тем самым обоснованно подойти к выбору системы и ее закона управления, удовлетворяющему выбранному критерию качества.
Комплекс требований, определяющих поведение автоматической системы в установившихся и переходных процессах отработки заданного воздействия, определяется понятием «качество процесса регулирования» или «качество автоматической системы».
Автоматическая система называется качественной, если она удовлетворяет определенным технологическим требованиям: например, как будет меняться реакция автоматической системы, если на ее вход действуют различного рода возмущения как по каналу управления, так по каналу возмущения, т. е. обеспечивается ли принципиальная возможность прихода автоматической системы в некоторое установившееся состояние. Такое понятие качества автоматической системы охватывает ее статические и динамические свойства, выраженные в количественной форме и получившие название показателей качества автоматического регулирования.
Мы уже знаем, что автоматическая система прежде всего должна быть устойчивой, однако это необходимое, но недостаточное условие для эффективной работы автоматической системы. В устойчивой системе переходный процесс затухает. Однако для практики вовсе не безразличен характер затухания переходного процесса. Так, например, если переходный процесс затухает медленно, и система долго входит в новый установившийся режим, то она обладает недостаточным быстродействием, и, следовательно, ее применение будет ограничено. Поэтому устойчивость является необходимым, но недостаточным условием работоспособности автоматических систем. Достаточным условием является качество процессов регулирования, которое оценивается качеством переходных процессов и ошибками в установившихся режимах.
Оценки качества работы автоматических систем, полученные непосредственно по кривым переходного процесса, называют прямыми. Вычисление всех этих критериев основывается на использовании математического аппарата управления, причем наиболее часто при вычислении критериев качества используются временные и частотные характеристики автоматических систем. Анализ переходных процессов сводится к отысканию общего решения неоднородного дифференциального уравнения, описывающего физические процессы в автоматической системе при заданных начальных условиях и известных внешних воздействиях, а также к анализу влияния изменения параметров автоматической системы на вид этого решения. Следует отметить, что аналитическое решение уравнений требует вычисления корней характеристического уравнения и вычисления постоянных интегрирования, что для уравнений выше третьего порядка невозможно.
Поэтому применяют приближенные методы анализа переходных процессов, не требующие, так же как и при исследовании устойчивости автоматических систем, непосредственного решения дифференциальных уравнений. Чаще всего при анализе качества работы автоматических систем требуется лишь установить, находится ли переходный процесс внутри области допустимых значений регулируемой величины или выходит за ее пределы. Оценки, получаемые этим методом, называют косвенными.
Прямые показатели качества переходных процессов. Качество переходных процессов обычно оценивают по переходной функции, которая представляет собой реакцию автоматической системы на внешнее воздействие типа единичного скачка. На примере переходной функции познакомимся с основными показателями качества переходного процесса:
1. Ошибка регулирования;
2. Время регулирования;
3. Перерегулирование;
4. Степень колебательности;
5. Количество колебаний.
Использование того или иного показателя работы автоматической системы или их комбинации в виде критериев качества определяется удобством его применения в системах автоматического регулирования, а также, в известной мере, сложившимися традициями.
Для статических автоматических систем определяется абсолютное e и относительное d значения ошибки регулирования. Относительное значение ошибки регулирования можно вычислить по выражению
Для астатических автоматических систем пользуются правилом, которое позволяет установить, устраняет ли астатический регулятор статическую ошибку от какого-либо либо возмущения. Для выполнения этого необходимо, чтобы интегрирующее звено было включено в цепь регулирования до места приложения данного возмущения. Это объясняет тот факт, что включение интегрирующих элементов и повышение степени астатизма не дает возможности устранить ошибку чувствительного элемента, которую можно рассматривать как возмущение.
В качестве второго типового режима используется режим движения с постоянной скоростью v = const, который будет наблюдаться в установившемся состоянии при задающем воздействии, изменяющимся по закону x (t) = v t и при постоянных значениях возмущающих воздействий. Этот режим преимущественно применяется в следящих системах и системах программного регулирования.
Третьим типовым режимом является установившееся движение с постоянным ускорением a = const. В этом случае задающее воздействие меняется по закону
Возмущающее воздействие принимается постоянным. Этот режим практически используется только в следящих системах и системах программного регулирования.
Четвертым типовым режимом является движение по гармоническому закону. Такой режим используется весьма часто, так как он позволяет наиболее полно оценить динамические свойства автоматической системы. Задающее воздействие изменяется по закону
В зависимости от конкретного вида автоматической системы возмущающие воздействия в рассматриваемом режиме могут оставаться постоянными или изменяться во времени.
Во всех режимах в зависимости от постоянства или изменения возмущающих воздействий появляется некоторая абсолютная e (t) или относительная d (t) постоянная ошибка. Более вероятным является случай, когда возмущающие воздействия при движении автоматической системы в этом режиме меняются во времени. то объясняется тем, что при движении по гармоническому закону непрерывно будет меняться направление движения автоматической системы, а следовательно, одновременно будет меняться напрявление действующих в автоматической системе сил сухого трения. Этот случай является довольно сложным, и он может рассматриваться только в приложении к конкретным автоматическим системам.
Апериодическая составляющая тока короткого замыкания
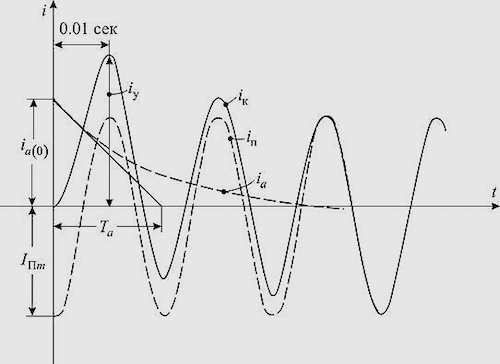
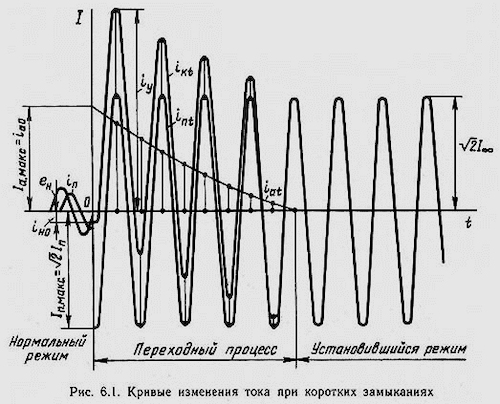
При наступлении режима КЗ постоянные токовые величины подвергаются существенным изменениям. В самое первое мгновение появляется так называемая апериодическая составляющая тока короткого замыкания, которая достаточно быстро угасает и принимает нулевое значение. Данный временной интервал, когда наблюдаются эти перемены, представляет собой переходный период, определяемый в числовом выражении. Пока аварийное состояние тока не будет отключено, работа электрической сети производится в установившемся режиме короткого замыкания.
Физические свойства апериодической составляющей
Подобное состояние тока возникает в момент короткого замыкания. Его продолжительность и характеристики могут быть разными, в зависимости от многих факторов. Например, при наличии у двигателя демпферной обмотки, апериодическая составляющая тока короткого замыкания будет ниже, чем при ее отсутствии. Вначале возникает сверхпереходный ток, который вначале становится просто переходным, и лишь потом он начинает затухать.
Во время двухфазного замыкания, в статоре не появляются скачкообразные изменения тока. В подобных ситуациях, на холостом ходе возникает апериодическая составляющая, параметры которой совпадают с начальной величиной переменной компоненты. Поскольку ток КЗ внутри статора является однофазным, в отдельных случаях появление апериодической компоненты полностью исключается. В двигателях асинхронного типа этот показатель не учитывается, поскольку данные процессы очень быстро затухают. Он не принимается во внимание даже при расчетных вычислениях ударных токов КЗ.
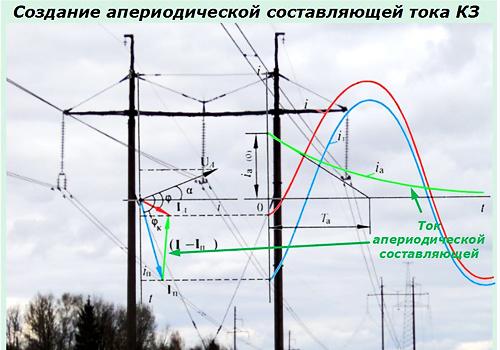
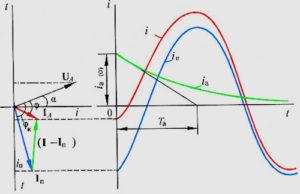
В общем и целом, величина данных компонентов будет отличаться для каждой фазы. Ее начальные параметры будут зависеть от момента появления КЗ. На графиках она представляет собой сплошную кривую линию, поскольку все начальные амплитуды других составляющих будут ей равны, но направлены в обратную сторону.
Наличие апериодической составляющей устанавливается при расхождении контактов. Для ее оценки существует специальный параметр, представляющий собой соотношение между ней и периодической амплитудой в момент размыкания контактов. Время затухания составляет примерно 0,1-0,2 с и сопровождается значительным выделением тепла. Под действием высокой температуры заметно нагреваются токоведущие части и вся аппаратура в целом, несмотря на столь короткий промежуток времени.
Полный ток при наступлении КЗ
Сама по себе апериодическая компонента не может быть рассмотрена, поскольку она является одной из составных частей тока короткого замыкания. В электрической сети присутствуют сопротивления индуктивного характера, не дающие току мгновенно изменяться в момент появления КЗ. Рост нагрузочного тока проистекает не скачкообразно, а согласно определенных законов, предполагающих переходный период от нормального к аварийному значению. Расчетно-аналитическая работа значительно упрощается, когда ток КЗ во время перехода рассматривается как две составные части – апериодическая и периодическая.
Апериодическая часть представляет собой составную часть тока ia с неизменной величиной. Она появляется непосредственно в момент КЗ и в кратчайший срок падает до нулевой отметки.
Периодическая часть тока КЗ Iпm получила название начальной, поскольку по времени она появляется в самом начале процесса. Данный показатель используется для того чтобы выбрать наиболее подходящую уставку или проверить чувствительность релейной защиты. Этот ток известен еще и как сверхпереходный, поскольку его определение осуществляется с помощью сверхпереходных сопротивлений, вводимых в схему замещения. Периодический ток считается установившимся, когда затухает апериодическая часть и заканчивается сам переходный процесс.
Следовательно, полный ток короткого замыкания будет составлять сумму обоих частей – апериодической и периодической во весь период перехода состояний. В определенный момент полный ток за кратчайшее время принимает максимальное значение. Подобное состояние известно под названием ударного тока КЗ, определяемого при проверках электродинамической устойчивости установок и оборудования.
Выбор начального или сверхпереходного тока для проведения расчетов определяет скорое угасание апериодической части, которое происходит раньше, чем срабатывает защита. При этом периодическая составляющая остается неизменной.
Электрические сети, подключенные к генераторным установкам или энергетической системе с ограниченной мощностью, отличаются значительным изменением напряжения при появлении КЗ. В связи с этим, токи, начальный и установившийся, не будут равны между собой. Для того чтобы сделать расчет релейной защиты, можно воспользоваться показателями изначального тока. В этом случае погрешность будет незначительной в сравнении с установившимся током, подверженным воздействию различных факторов. Прежде всего, это увеличенное сопротивление в поврежденной точке, нагрузочные токи и прочие параметры, которые чаще всего не учитываются при выполнении расчетов.
Как вычислить апериодическую компоненту
Первоначальная величина апериодической части в модульном выражении определяется как разница между мгновенным показателем периодической части в начале КЗ и величиной тока непосредственно перед замыканием. То есть, апериодическая составляющая с максимальным первоначальным значением, сравняется с амплитудными параметрами периодической части тока при появлении КЗ. Это утверждение определяет формула: ia0 = √2Iп0, действующая при условии сниженной активной доли сопротивления в точке КЗ относительно индуктивной составляющей.
1. 
2. 
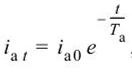
Кроме того, перед началом замыкания в расчетной точке не должно быть нагрузки, а напряжение какой-либо фазы к этому времени проходит по нулевому проводнику. Если же перечисленные требования не будут выполнены, то апериодическая часть в первоначальной стадии снизит свои показатели по отношению к амплитуде периодической составляющей.
Для того чтобы выполнить расчет апериодической составляющей тока короткого замыкания в любое произвольное время, заранее прорабатывается вариант замещения. Согласно первоначальной расчетной схеме, все составные элементы учитываются в качестве активных и индуктивных сопротивлений. Учет синхронных генераторов и компенсаторов, асинхронных и синхронных электродвигателей проводится путем перевода их в категорию индуктивных сопротивлений с обратной последовательностью. Обязательно учитываются сопротивления обмоток статора постоянному току с рабочей температурой установленной нормы.
3. 
Когда в изначальной схеме расчетов присутствуют лишь компоненты, соединенные последовательно, в этом случае величина апериодической доли в любой момент времени определяется формулой 1, в которой Та является постоянной величиной, определяющей время затухания данной части. В свою очередь, Та можно вычислить по формуле 2, в которой Xэк и Rэк будут индуктивной и активной составляющими, а ωсинх является синхронной угловой частотой сетевого напряжения. Если же при расчетах необходимо учесть величину генераторного тока непосредственно перед коротким замыканием, тогда уже используется формула 3.
Особенности вычислений в многоконтурных схемах
Если в расчетах используются многоконтурные схемы, тогда на апериодическую составляющую не действует экспоненциальный закон временного изменения. Фактически, она выглядит в виде суммы токов, каждый из которых является экспоненциальной временной функцией и угасает в различные интервалы времени. Количество таких компонентов в цепях с активными и индуктивными ветвями, совпадает с численностью независимых контуров.
В этом случае апериодические составляющие могут быть вычислены с использованием специальных систем дифференциальных уравнений, учитывающих все активные и индуктивные сопротивления. Методика расчетов во многом зависит от того, как выглядит изначальная схема расчетов, и где расположена рассчитываемое место КЗ.
В некоторых вариантах источники энергии многоконтурной схемы замыкаются на расчетное место КЗ с помощью общего сопротивления. Приближенные расчеты позволяют установить затухание апериодической составляющей в течение какого-то постоянного промежутка времени. Существуют два метода решений, которые, относительно точного результате выдают погрешность с положительной или отрицательной направленностью. То есть, постоянная времени будет завышаться или занижаться.
Расчетная схема, разделенная точкой короткого замыкания на части, независимые между собой, в произвольный момент времени определяется в виде суммы апериодических составляющих, предусмотренных для каждого участка схемы. Их изменение по времени происходит относительно постоянного показателя, а полученные данные учитываются в расчетах.
Ударный ток короткого замыкания
Ток короткого замыкания однофазных и трехфазных сетей
Что показывает постоянная времени процесса затухания
Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и 
(рис. 3.1):
,
где β – коэффициент затухания.
Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
;
.
Выясним физический смысл χ и β.
Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
отсюда 
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
; 
;
.
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Если χ = 0,01, то N = 100.
При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому 
, а 
то круговая частота обращается в нуль ( 
), а ( 
), колебания прекращаются. Такой процесс называется апериодическим (рис. 3.2).
Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.