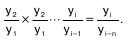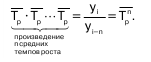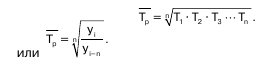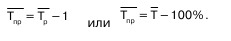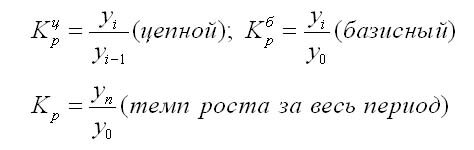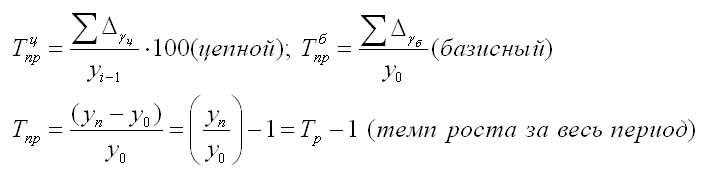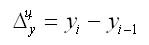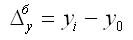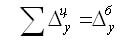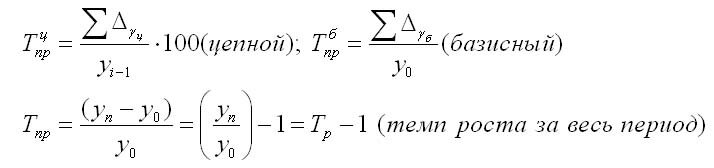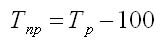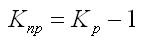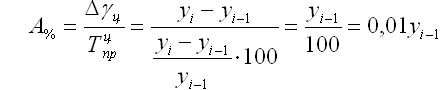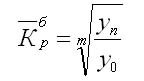Что показывает средний темп прироста в статистике
Формула темпа прироста
Понятие и значение темпа прироста
Темп прироста используется при анализе какого-либо ряда динамики. Формула темпа прироста часто применяется в статистике и экономике в паре с таким показателем, как темп роста (в процентном соотношении).
Если в результате расчета получается положительная величина, то можно говорить об увеличивающемся темпе прироста, при отрицательном же значении происходит снижение темпа исследуемого значения, если сравнивать его с предыдущим (базисным) периодом.
Формула темпа прироста часто применяется в анализе инвестиционных проектов. Также этот показатель часто используется муниципальными организациями при расчетах:
Формула темпа прироста
Для расчета темпа прироста нужно найти отношение исследуемого показателя к предыдущему (базисному), далее из получаемого результата вычесть единицу. Окончательный результат умножается на 100, для того, что бы выразить итог в процентах. Формула темпа прироста по первому способу выглядит так:
Тп=((Пип/Пбп)-1)*100%
Здесь Тп – темп прироста,
Пбп – показатель базисного периода,
Пип – показатель исследуемого периода.
В случае, когда вместо фактического значения анализируемых показателей известно только значение абсолютного прироста, применяют альтернативную формулу. При этом находят процентное отношение абсолютного прироста к тому уровню, в сравнении с которым он и рассчитывался.
Тп=((Пип-Пбп)/Пбп)*100%
Здесь Тп – темп прироста,
Пбп – показатель базисного периода,
Пип – показатель исследуемого периода.
Отличие темпа роста и темпа прироста
Большую сложность для учащихся представляет отличие темпа роста от темпа прироста. Выделим несколько положений, в которых заключается разница между этими величинами:
Примеры решения задач
| Задание | Для предприятия ООО «Севермет» даны следующие показатели, представленные за 2015 и 2016 год: |
2015 год – 120млн. рублей,
2016 год – 110,4млн. рублей.
Известно, что в 2017 году величина дохода увеличилась в сравнении с 2016 годом на 25 млн. рублей.
На основе имеющихся данных рассчитать темп роста и прироста, сделав при этом выводы.
Здесь Тр – темп роста,
П2015 – показатель за 2015 год,
П2016 – показатель за 2016 год.
Тр=110,4млн. руб./120млн. руб. * 100% = 92 %
Темп прироста обозначает процентное соотношение изменения величины в текущем периоде в сравнении с предыдущим. Для расчета нужна формула темпа прироста:
Рассчитаем показатели за 2017 год
Тр=(120 млн. руб. + 25 млн. руб.)/120 млн. руб.= 1,21 (или 121 %)
Тп=(145 млн. руб./120 млн. руб)-1=0,208 (или 20,8%)
Вывод. Мы видим, что темп роста при сравнении 2015 и 2016 года составил 92%. Это означает, что прибыль предприятия в 2016 году уменьшилась на 92%в сравнении с 2015 годом. При расчете темпа прироста получилась отрицательная величина (-8%), что говорит о том, что прибыль компании в 2016 году (при сравнении с 2015 годом) уменьшилась на 8%. В 2017 году прибыль составила 121% в сравнении с 2016 годом. При расчете темпа прироста мы видим, что он составил 20,8%. Положительная величина говорит об увеличении прибыли именно на это количество процентов.
| Задание | Рассчитать прирост заработной платы на предприятии ООО «Севермет» за 2015 и 2016 год. Даны следующие показатели: |
Заработная плата 2015 год – 31,5 тыс. руб.,
заработная плата 2016 год – 33 тыс. руб.,
Вывод: Таким образом, мы видим, что темп прироста составил 4,8 %, что означает, что заработная плата в 2016 году по сравнению с 2015 годом увеличилась на 4,8%.
Средний абсолютный прирост
Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим в среднем за единицу времени. Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем. Он вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени:
В качестве основы и критерия правильности исчисления среднего темпа роста (как и среднего абсолютного прироста) можно использовать в роли определяющего показателя произведение цепных темпов роста, которое равно темпу роста за весь рассматриваемый период. Таким образом, перемножив n цепных темпов роста, получается темп роста за весь пе риод:
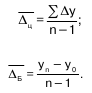
Должно соблюдаться равенство:
Данное равенство представляет формулу простой средней геометрической Из этого равенства следует:
Средний темп роста, выраженный в форме коэффициента, показывает, во сколько раз увеличивался уровень по сравнению с предыдущим в среднем за единицу времени.
Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, которая имеет место между обычными темпами роста и прироста:
Средний темп прироста (или снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или снижался) уровень по сравнению с предыдущим в среднем за единицу времени. Средний темп прироста характеризует среднюю интенсивность роста.
Из двух видов формулы среднего темпа роста чаще используется вторая, так как она не требует вычисления всех цепных темпов роста. По первой формуле расчет целесообразно производить лишь в тех случаях, когда не известны ни уровни ряда динамики, ни темп роста за весь период, а известны только цепные темпы роста (или прироста).
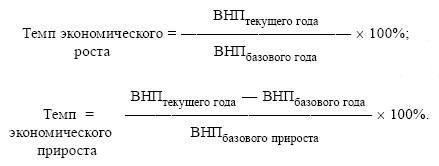
Показатели динамики: темп роста и темп прироста
Темп роста
Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.
Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста
Коэффициент роста может быть рассчитан по формулам:
Также темп роста может определяться так:
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.
Абсолютный прирост
Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:
1. Абсолютный прирост (цепной):
2. Абсолютный прирост (базисный):
где уi — уровень сравниваемого периода;
Уi-1 — Уровень предшествующего периода;
У0 — уровень базисного периода.
Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.
Темп прироста
Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:
Темп прироста можно получить из темпа роста:
Коэффициент прироста может быть получен таким образом:
Абсолютное значение 1%-го прироста
Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.
Примеры расчетов показателей динамики
Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики
О показателях динамики
При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.
Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.
Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.
Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста
Средний уровень ряда в статистике
Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.
Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:
1. При равных интервалах используют среднюю арифметическую простую:
где у — абсолютные уровни ряда;
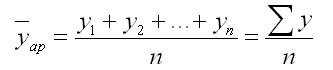
n — число уровней ряда.
2. При неравных интервалах используют среднюю арифметическую взвешенную:
где у1,…,уn — уровни ряда динамики;
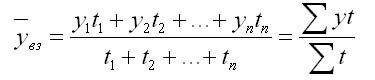
t1,… tn — веса, длительность интервалов времени.
Средний уровень моментного ряда динамики рассчитывается по формуле:
1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:
где у1,…,уn — уровни периода, за который делается расчет;
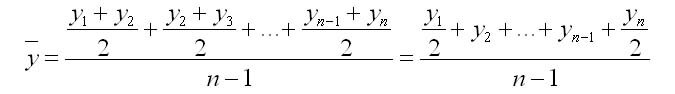
n — число уровней;
n-1 — длительность периода времени.
2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:
где у1,…,уn — уровни рядов динамики;
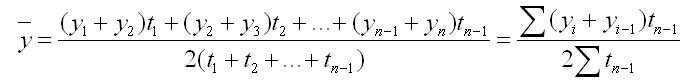
t — интервал времени между смежными уровнями
Средний абсолютный прирост в задачах статистики
Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:
1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
где n — число степенных абсолютных приростов в исследуемом периоде.
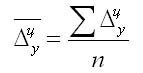
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов
где m — число уровней ряда динамики в исследуемом периоде, включая базисный.
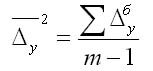
Средний темп роста
Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:
где n — число цепных коэффициентов роста;
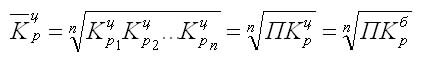
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:
Средний темп прироста
Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:
Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
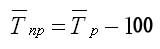
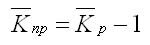
13 Ряды динамики
Статистическое изучение динамики социально-экономических явлений
Процессы и явления социально-экономической жизни общества, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении. Для того, чтобы выявить тенденции и закономерности социально-экономического развития явлений, статистика строит особые ряды статистических показателей, которые называются рядами динамики (иногда их называют временными рядами), то есть ‑ это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В англоязычной литературе для временных рядов используется термин «time series». Ряды динамики получаются в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. Значения показателя, составляющие ряд динамики, называются уровнями ряда.
Каждый ряд динамики характеризуется двумя параметрами: значениями времени и соответствующими им значениями уровней ряда. Уровни ряда обычно обозначаются «yt»: y1, y2 и т.д. В качестве показателя времени в рядах динамики могут указываться отдельные периоды (сутки, месяцы, кварталы, годы и т.д.) времени или определенные моменты (даты). Время в рядах динамики обозначается через «t».
Ряд динамики состоит из двух элементов:
1) уровня ряда (значения изучаемого показателя);
2) моментов (периодов) времени, когда фиксируется этот показатель.
Основные способы обработки рядов динамики:
1) укрупнение интервалов и расчет для них средних показателей;
2) сглаживание уровней способом скользящей средней;
3) выравнивание по аналитическим формулам.
Суть последнего способа заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени.
Ряды динамики, как правило, представляют в виде таблицы или графически.
Ряды динамики могут быть классифицированы по следующим признакам:
В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин ‑ как производные.
Ряды динамики абсолютных величин наиболее полно характеризуют развитие процесса или явления, например, грузооборота транспорта, инвестиций в основной капитал, добычи топлива, уставного капитала коммерческих банков и т.д.
Ряды относительных величин могут характеризовать во времени темпы роста (или снижения) определенного показателя; изменение удельного веса того или иного показателя в совокупности или изменение показателей интенсивности отдельных явлений, например, удельного веса приватизированных предприятий в той или иной отрасли; производства продукции на душу населения; структуры инвестиций в основной капитал по отраслям экономики, индекса потребительских цен и т.д.
Ряды динамики средних величин служат для характеристики изменения уровня явления, отнесенного к единице совокупности, например: данные о среднегодовой численности занятых в экономике; о средней урожайности отдельных сельскохозяйственных культур, о средней заработной плате в отдельных отраслях и т.д.
В зависимости от характера временного параметра ряды динамики делятся на моментные и интервальные.
Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени.
Пример. Моментный ряд динамики, характеризующий численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г., представлен в таблице 13.1.
Таблица 13.1 ‑ Численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г
| Дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 |
| Численность персонала, чел. | 780 | 810 | 880 | 930 | 940 | 970 |
Следует помнить, что моментные ряды абсолютных величин нельзя суммировать. Бессмысленно, например, складывать численность персонала по состоянию на 1 января, 1 февраля и т.д. Полученная сумма ничего не выражает, так как в ней многократно повторяются одни и те же единицы совокупности.
Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным.
Пример. Интервальный ряд динамики, представлен в таблице 13.2.
Таблица 13.2. ‑ Характеристика динамики объема розничного товарооборота
| Дата | 2004 | 2005 | 2006 | 2007 | 2008 |
| Товарооборот, млн. руб. | 28,3 | 31,9 | 38,3 | 42,3 | 45,2 |
Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда вполне реальный показатель, например, общий объем розничного товарооборота за 2004-2008 г.г.
В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и не равноотстоящими уровнями во времени.
Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими, пример (табл. 13.1 и табл. 13.2).
Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются не равноотстоящими, пример(табл. 13.3).
Пример. Рядом динамики с не равноотстоящими уровнями во времени может служить объем экспорта продукции предприятия, представленный в таблице 13.3.
Таблица 13.3. – Динамика объема экспорта продукции предприятия
| Годы | 1993 | 1996 | 1998 | 2000 | 2004 |
| Объем экспорта, млн. долл. | 1110 | 1220 | 1320 | 1450 | 1640 |
По числу показателей можно выделить изолированные (одномерные) и комплексные (многомерные) ряды динамики.
Если ведется анализ во времени одного показателя ряда, то ряд динамики изолированный (например, данные о производстве газа по годам). В многомерном ряду представлена динамика нескольких показателей, характеризующих одно явление.
Сопоставимость уровней и смыкание рядов динамики
Важнейшим условием правильного построения рядов динамики является сопоставимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
Рассмотрим основные причины несопоставимости уровней ряда динамики.
Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения и единиц счета.
Пример. Нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы оно дано в погонных метрах, а за другие ‑ в квадратных метрах.
На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.
Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие ‑ с убранной, то такие уровни будут несопоставимы.
В процессе развития во времени, прежде всего, происходят количественные измерения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерностей явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, разделять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития.
Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл.
Например, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с данными 1 января, так как первая цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставленный на зимовку. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.
Несопоставимость уровней ряда может возникнуть вследствие изменений территориальных границ областей, районов и так далее.
Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых являются несопоставимыми. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).
Пример. Предположим, что в N-ом регионе имеются данные об общем объеме оборота розничной торговли за 2013-2015 гг. в фактически действующих ценах, и за 2015-2018 гг. ‑ в сопоставимых ценах (табл. 13.4.).
Таблица 13.4 ‑ Динамика общего объема оборота розничной торговли (млрд. руб.) цифры условные