Что показывает стандартная ошибка

Понятие об ошибке выборки.

Поможем написать любую работу на аналогичную тему

Стандартная ошибка статистики, т.е. оценка стандартного отклонения ее выборочного распределения, приближенно показывает, насколько значение статистики может отличаться от своего среднего значения (параметра генеральной совокупности).

Стандартная ошибка среднего (или просто стандартная ошибка) приближенно показывает, насколько ее выборочная средняя (случайная наблюдаемая величина) отличается от среднего генеральной совокупности μ (фиксированная неизвестная величина):

(7.1)

Стандартная ошибка уменьшается с увеличением размера выборки n (при прочих равных условиях), отражая тот факт, что большая по размеру выборка содержит больше информации и таким образом достигается большая точность.

Когда объем генеральной совокупности настолько мал, что выборка составляет достаточно большую часть генеральной совокупности, стандартную ошибку можно уменьшить, введя в формулу корректирующий (поправочный) коэффициент для конечной совокупности, чтобы получить уточненную (откорректированную) стандартную ошибку:

(7.2)

Кроме того, формулу (7.1) используют повторной выборке, а формулу (7.2) – для бесповторной, однако, если объем выборочной совокупности достаточно большой, то поправочный коэффициент не играет большой роли и стандартная ошибка для бесповторной выборки определяется по формуле (7.1).

Для измерения стандартной ошибки доли альтернативного признака применяют другие формулы. При повторной выборке:

(7.3)

При бесповторной выборке:

(7.4)

Теоретическую (идеальную) генеральную совокупность можно определить; как очень большую, иногда предполагаемую (воображаемую) генеральную совокупность, которую представляет ваша выборка. Если вас интересует теоретическая генеральная совокупность, не используйте поправку на конечность генеральной совокупности. С другой стороны, если необходимо сделать вывод об основе выборки, не выходя за ее пределы, то поправка может быть полезной, так как ее использование уменьшает вариацию системы. Если есть сомнения, лучше не использовать поправку.

Стандартная ошибка доли показывает неопределенность, или изменчивость, в наблюдаемой доле , а стандартная ошибка среднего–неопределенность в наблюдаемой частоте х.

Доверительным интервалом называют интервал, рассчитанный из данных таким образом, что существует известная вероятность включения интересующего вас (неизвестного) параметра генеральной совокупности в интервал, и эта вероятность интерпретируется с точки зрения случайного эксперимента начинающегося с извлечения случайной выборки. Границы доверительного интервала определяются на основе точечной оценки и предельной ошибки выборки, которая равна произведению стандартной ошибки и — критерия Стьюдента. Предельная ошибка выборки показывает максимально возможную ошибку для принятой вероятности, а доверительное число – как соотносятся предельная и стандартная ошибки.

(7.3)

Вероятность того, что параметр совокупности будет принадлежать доверительному интервалу называют уровнем доверительности, который обычно устанавливают равным 95%, хотя часто используют и другие уровни – 90; 99; 99,9%. Чем выше уровень доверительности, тем шире (а значит, и менее полезен) доверительный интервал. Приблизительная обобщенная формулировка утверждения о доверительном интервале имеет следующий вид: мы уверены на 95%, что значение параметра генеральной совокупности находится между значением оценки минус две стандартные ошибки оценки и значением оценки плюс две стандартные ошибки оценки.

Это утверждение основано на том факте, что при нормальном распределении с вероятностью 0,95 следует ожидать значения на расстоянии , т.е. приблизительно два стандартных отклонения от среднего.

Формулировка утверждения о двустороннем 95% доверительном интервале для среднего генеральной совокупности имеет следующий вид:

мы уверены, на 95%, что среднее генеральной совокупности m находится между и , где значение t берется из t-таблицы.

(7.4)

Формулировка утверждения о двустороннем 95% доверительном интервале для генеральной доли имеет следующий вид:

мы уверены на 95%, что доля интересующего нас свойства в генеральной совокупности р находится между и , где значение t берется из t-таблицы.

(7.5)

Чтобы получить доверительный уровень, отличный от 95%, следует просто при построении доверительного интервала использовать соответствующее значение. t-таблицу используют для коррекции дополнительной неопределенности, обусловленной тем, что вместо неизвестного точного значения изменчивости генеральной совокупности используют оценку (стандартную ошибку). Когда вы работаете с бесповторной выборкой размера п, число степеней свободы, равное , представляет собой количество независимых элементов информации, использованных при вычислении стандартной ошибки (поскольку при вычислении стандартного отклонения из наблюдаемых значений вычитают среднее). Если известно точное значение стандартной ошибки, используют t-значение для бесконечного числа степеней свободы.

Для того чтобы использование доверительного интервала было корректным, необходимо выполнение двух следующих условий:

(1) данные должны представлять собой случайную выборку из рассматриваемой генеральной совокупности;

(2) измеренные значения должны подчиняться нормальному распределению.

Первое условие гарантирует, что данные правильно представляют неизвестный параметр, а второе дает основание использовать t-таблицу для вычисления вероятности.

Односторонний доверительный интервал с известной доверительностью указывает, что среднее генеральной совокупности либо не меньше, либо не больше некоторого вычисленного значения. Граничное значение для одностороннего доверительного интервала вычисляется таким же образом, как и для двустороннего интервала, только t-значение для двустороннего интервала заменяется на t-значение для одностороннего интервала и выбирается граничная точка интервала так, чтобы построенный односторонний интервал включал выборочное среднее .

При использовании одностороннего интервала вы должны быть уверены, что независимо от поведения данных вы будете использовать односторонний интервал с той же стороны (т.е. открытый в сторону больших значений или открытый в сторону меньших значений). В противном случае использование одностороннего доверительного интервала некорректно. При наличии сомнений лучше использовать двусторонний интервал. Утверждение об одностороннем доверительном интервале формулируется следующим образом:

мы уверены на 95%, что среднее генеральной совокупности не меньше, чем ; или мы уверены на 95%, что среднее генеральной совокупности не больше, чем .

Интервал предсказания позволяет использовать данные выборки для предсказания с известной вероятностью значения нового наблюдения при условии, что это новое наблюдение получено тем же способом, что и предшествующие. В качестве меры неопределенности здесь используется стандартная ошибка предсказания , мера изменчивости расстояния между средним значением выборки и новым наблюдением. Интервал предсказания строят тем же способом, что и доверительный интервал; просто заменяют стандартную ошибку среднего на, стандартную ошибку предсказания. Формулировка утверждения об интервале предсказания (двустороннем) для значения нового наблюдения будет следующей:

Мы уверены на 95%, что новое наблюдение будет находиться между и .

Формулировка утверждения об интервале предсказания (одностороннем) для значения нового наблюдения будет такой:

Мы уверены на 95%, что новое наблюдение будет не меньше, чем ; или мы уверены на 95%, что новое наблюдение будет не больше, чем .

Выбирая соответствующие t-значение из таблицы, интервалы предсказания для уровней доверительности, отличных от 95%, необходимо помнить, что доверительный интервал дает информацию о среднем генеральной совокупности, в то время как интервал предсказания дает информацию о единственном наблюдении, случайно выбранном из той же генеральной совокупности.

Источник

Стандартная ошибка

Что такое Стандартная ошибка?

Стандартная ошибка (SE) статистики – это приблизительное стандартное отклонение статистической выборки. Стандартная ошибка – это статистический термин, который измеряет точность, с которой выборочное распределение представляет генеральную совокупность с помощью стандартного отклонения. В статистике выборочное среднее отклоняется от фактического среднего для генеральной совокупности; это отклонение представляет собой стандартную ошибку среднего.

Ключевые моменты

Понимание стандартной ошибки

Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных статистических данных выборки, таких как среднее или медианное значение. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из генеральной совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности.

Связь между стандартной ошибкой и стандартным отклонением такова, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень из размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; Чем больше размер выборки, тем меньше стандартная ошибка, поскольку статистика приближается к фактическому значению.

Стандартная ошибка считается частью выводимой статистики. Он представляет собой стандартное отклонение среднего значения в наборе данных. Это служит мерой вариации случайных величин, обеспечивая измерение спреда. Чем меньше разброс, тем точнее набор данных.

Краткая справка

Стандартная ошибка и стандартное отклонение – это меры изменчивости, в то время как меры центральной тенденции включают среднее значение, медианное значение и т. Д.

Требования к стандартной ошибке

В случаях, когда собирается несколько образцов, среднее значение каждой выборки может незначительно отличаться от других, создавая разброс между переменными. Этот разброс чаще всего измеряется как стандартная ошибка, учитывающая различия между средними значениями в наборах данных.

Чем больше точек данных участвует в расчетах среднего, тем меньше стандартная ошибка. Когда стандартная ошибка мала, данные считаются более репрезентативными для истинного среднего значения. В случаях, когда стандартная ошибка велика, данные могут иметь некоторые заметные отклонения.

Стандартное отклонение – это представление разброса каждой точки данных. Стандартное отклонение используется для определения достоверности данных на основе количества точек данных, отображаемых на каждом уровне стандартного отклонения. Стандартные ошибки больше служат способом определения точности образца или точности нескольких образцов путем анализа отклонения в пределах средних.

Источник

Стандартная ошибка среднего и стандартного отклонения: разница

Опубликовано 30.06.2021 · Обновлено 30.06.2021

Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.

Ключевые выводы

SEM против SD

Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD – это разброс отдельных значений данных.

Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM – это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).

Расчет стандартного отклонения

Формула SD требует нескольких шагов:

Стандартная ошибка среднего

SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.

Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.

Стандартная ошибка и стандартное отклонение в финансах

В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.

С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.

Источник

Стандартная ошибка

В случае несмещенного оценщика стандартная ошибка, следовательно, является мерой среднего отклонения оцененного значения параметра от истинного значения параметра. Чем меньше стандартная ошибка, тем точнее неизвестный параметр можно оценить с помощью оценщика. Стандартная ошибка зависит, помимо прочего, от

Как правило, чем больше размер выборки, тем меньше стандартная ошибка; чем меньше дисперсия, тем меньше стандартная ошибка.

оглавление

интерпретация

Стандартная ошибка дает представление о качестве оцениваемого параметра. Чем больше имеется индивидуальных значений, тем меньше стандартная ошибка и тем точнее можно оценить неизвестный параметр. Стандартная ошибка делает измеренный разброс (стандартное отклонение) двух наборов данных с разными размерами выборки сопоставимым путем нормализации стандартного отклонения к размеру выборки.

пример

обозначение

оценивать

Доверительные интервалы и тесты

или сформулировать тесты, например Б. принимает ли параметр определенное значение : ϑ 0 <\ displaystyle \ vartheta _ <0>>

ЧАС 0 : ϑ знак равно ϑ 0 <\ displaystyle H_ <0>: \ vartheta = \ vartheta _ <0>> против. ЧАС 1 : ϑ ≠ ϑ 0 <\ displaystyle H_ <1>: \ vartheta \ neq \ vartheta _ <0>>

а результаты статистики теста:

Стандартная ошибка среднего арифметического

Стандартная ошибка среднего арифметического такая же

σ ( Икс ¯ ) знак равно σ п <\ Displaystyle \ sigma (<\ overline >) = <\ гидроразрыва <\ sigma><\ sqrt >>> ,

Вывод

Икс ¯ знак равно 1 п ∑ я знак равно 1 п Икс я <\ displaystyle <\ overline > = <\ frac <1>> \ sum _ ^ X_ >

σ ( Икс ¯ ) 2 знак равно Вар ⁡ ( Икс ¯ ) знак равно Вар ⁡ ( 1 п ∑ я знак равно 1 п Икс я ) знак равно 1 п 2 Вар ⁡ ( ∑ я знак равно 1 п Икс я ) знак равно 1 п 2 ∑ я знак равно 1 п Вар ⁡ ( Икс я ) знак равно 1 п 2 п σ 2 знак равно σ 2 п <\ displaystyle \ sigma (<\ overline >) ^ <2>= \ operatorname \ left (<\ overline > \ right) = \ operatorname \ left ( <\ frac < 1>> \ sum _ ^ X_ \ right) = <\ frac <1>>> \ operatorname \ left (\ sum _ ^ X_ \ right) = <\ frac <1>>> \ sum _ ^ \ operatorname \ left (X_ \ right) = <\ frac <1>>> n \ sigma ^ <2>= <\ frac <\ sigma ^ <2>> >>

σ ( Икс ¯ ) 2 знак равно 1 п 2 ∑ я знак равно 1 п σ я 2 <\ displaystyle \ sigma (<\ overline >) ^ <2>= <\ frac <1>>> \ sum _ ^ \ sigma _ ^ <2>> .

Предполагая выборочное распределение, стандартная ошибка может быть рассчитана с использованием дисперсии выборочного распределения:

пример

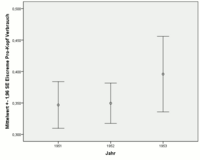
Для данных по мороженому рассчитывались среднее арифметическое, стандартная ошибка и стандартное отклонение за 1951, 1952 и 1953 годы для потребления мороженого на душу населения (измеряемого в пинтах ).

Для 1951 и 1952 годов расчетные средние значения и стандартные отклонения, а также числа наблюдений примерно одинаковы. Следовательно, оцененные стандартные ошибки также дают примерно такое же значение. В 1953 г., с одной стороны, количество наблюдений меньше, а стандартное отклонение больше. Таким образом, стандартная ошибка почти вдвое превышает стандартные ошибки 1951 и 1952 годов.

Здесь также ясно видно, что среднее значение для 1953 г. может быть оценено более неточно, чем средние значения для 1951 и 1952 гг. (Более длинная полоса для 1953 г.).

Стандартная ошибка коэффициентов регрессии в модели простой регрессии

Пример : Для данных по мороженому была проведена простая линейная регрессия для потребления мороженого на душу населения (измеренного в поллитрах) со средней недельной температурой (в градусах Фаренгейта) в качестве независимой переменной. Оценка регрессионной модели привела к:

Потребление на душу населения знак равно 0,206 86 + 0,003 11 ⋅ температура <\ displaystyle <\ text <Потребление на душу населения>> = 0 <,>20686 + 0 <,>00311 \ cdot <\ text <Температура>>> .

Хотя расчетный коэффициент регрессии для средней недельной температуры очень мал, расчетная стандартная ошибка дала еще меньшее значение. Точность оценки коэффициента регрессии в 6,5 раз меньше, чем самого коэффициента.

Отношение к логарифмической вероятности

Источник