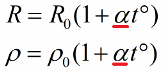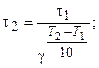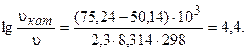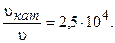Температурный коэффициент электрического сопротивления

Из Википедии — свободной энциклопедии

Температу́рный коэффицие́нт электри́ческого сопротивле́ния — величина, равная относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу.

Температурный коэффициент сопротивления характеризует зависимость электрического сопротивления от температуры и измеряется в кельвинах в минус первой степени (K −1 ).

Также часто применяется термин «температурный коэффициент проводимости». Он равен значению коэффициента сопротивления с обратным знаком.

Для большинства металлов температурный коэффициент сопротивления положителен: их сопротивление растёт с ростом температуры вследствие рассеяния электронов на фононах (тепловых колебаниях кристаллической решётки).

Для полупроводников без примесей он отрицателен (сопротивление с ростом температуры падает), поскольку при повышении температуры всё большее число электронов переходит в зону проводимости, соответственно увеличивается и концентрация дырок. Качественно такой же характер (и по тем же причинам) имеет температурная зависимость сопротивления твёрдых и неполярных жидких диэлектриков. Полярные жидкости уменьшают своё удельное сопротивление с ростом температуры более резко вследствие роста степени диссоциации и уменьшения вязкости. На практике этот эффект применялся для защиты электронных ламп от пусковых токов (см. Урдокс).

Температурная зависимость сопротивления металлических сплавов, газов, легированных полупроводников и электролитов носит более сложный характер.

Существуют сплавы (константан, манганин), имеющие очень малый температурный коэффициент сопротивления, то есть их сопротивление очень слабо зависит от температуры. Эти сплавы применяются в электроизмерительной аппаратуре.

Источник

Температурный коэффициент сопротивления

Электрическое сопротивление проводника в общем случае зависит от материала проводника, от его длины и от поперечного сечения, или более кратко — от удельного сопротивления и от геометрических размеров проводника. Данная зависимость общеизвестна и выражается формулой:

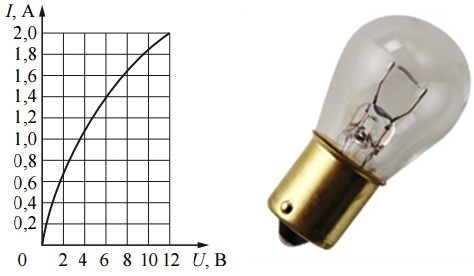
Известен каждому и закон Ома для однородного участка электрической цепи, из которого видно, что ток тем меньше, чем сопротивление выше. Таким образом, если сопротивление проводника постоянно, то с ростом приложенного напряжения ток должен бы линейно расти. Но в реальности это не так. Сопротивление проводников не постоянно.

За примерами далеко ходить не надо. Если к регулируемому блоку питания (с вольтметром и амперметром) подключить лампочку, и постепенно повышать напряжение на ней, доводя до номинала, то легко заметить, что ток растет не линейно: с приближением напряжения к номиналу лампы, ток через ее спираль растет все медленнее, причем лампочка светится все ярче.

Нет такого, что с увеличением вдвое приложенного к спирали напряжения, вдвое возрос и ток. Закон Ома как-будто не выполняется. На самом деле закон Ома выполняется, и точно, просто сопротивление нити накала лампы непостоянно, оно зависит температуры.

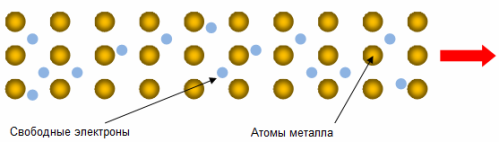
Вспомним, с чем связана высокая электрическая проводимость металлов. Она связана с наличием в металлах большого количества носителей заряда — составных частей тока — электронов проводимости. Это электроны, образующиеся из валентных электронов атомов металла, которые для всего проводника являются общими, они не принадлежат каждый отдельному атому.

Под действием приложенного к проводнику электрического поля, свободные электроны проводимости переходят из хаотичного в более-менее упорядоченное движение — образуется электрический ток. Но электроны на своем пути встречают препятствия, неоднородности ионной решетки, такие как дефекты решетки, неоднородная структура, вызванные ее тепловыми колебаниями.

Электроны взаимодействуют с ионами, теряют импульс, их энергия передается ионам решетки, переходит в колебания ионов решетки, и хаос теплового движения самих электронов усиливается, от того проводник и нагревается при прохождении по нему тока.

В диэлектриках, полупроводниках, электролитах, газах, неполярных жидкостях — причина сопротивления может быть иной, однако закон Ома, очевидно, не остается постоянно линейным.

Таким образом, для металлов, рост температуры приводит к еще большему возрастанию тепловых колебаний кристаллической решетки, и сопротивление движению электронов проводимости возрастает. Это видно по эксперименту с лампой: яркость свечения увеличилась, но ток возрос слабее. То есть изменение температуры повлияло на сопротивление нити накаливания лампы.

В итоге становится ясно, что сопротивление металлических проводников зависит почти линейно от температуры. А если принять во внимание, что при нагревании геометрические размеры проводника меняются слабо, то и удельное электрическое сопротивление почти линейно зависит от температуры. Зависимости эти можно выразить формулами:

Данный коэффициент численно равен относительному изменению электрического сопротивления проводника при изменении его температуры на 1К (на один градус Кельвина, что равноценно изменению температуры на один градус Цельсия).

Для металлов ТКС (температурный коэффициент сопротивления α) хоть и относительно мал, но всегда больше нуля, ведь при прохождении тока электроны тем чаще сталкиваются с ионами кристаллической решетки, чем выше температура, то есть чем выше тепловое хаотичное их движение и чем выше их скорость. Сталкиваясь в хаотичном движении с ионами решетки, электроны металла теряют энергию, что мы и видим в результате — сопротивление при нагревании проводника возрастает. Данное явление используется технически в термометрах сопротивления.

Что касается чистых полупроводников, то для них ТКС отрицателен, то есть сопротивление снижается с ростом температуры, это связано с тем, что с ростом температуры все больше электронов переходят в зону проводимости, растет при этом и концентрация дырок. Этот же механизм свойственен для жидких неполярных и твердых диэлектриков.

Полярные жидкости свое сопротивление резко уменьшают с ростом температуры из-за снижения вязкости и роста диссоциации. Это свойство применяется для защиты электронных ламп от разрушительного действия больших пусковых токов.

У сплавов, легированных полупроводников, газов и электролитов тепловая зависимость сопротивления более сложна чем у чистых металлов. Сплавы с очень малым ТКС, такие как манганин и константан, применяют в электроизмерительных приборах.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Правило Вант-Гоффа. Температурный коэффициент ско­рости реакции

Зависимость скорости реакции от температуры приближенно определяется эмпирическим правилом Вант-Гоффа: при изменении температуры на каждые 10 градусов скорость большинства реакций изменяется в 2-4 раза.

Математически правило Вант-Гоффа выражается так:

(3.6)

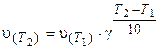
где v(T2) и v(T1) — скорости реакций, соответственно при температурах Т2 и T1 (T2> T1);

γ-температурный коэффициент скорости реакции.

Значение γ для эндотермической реакции выше, чем для экзотермической. Для многих реакций γ лежит в пределах 2-4.

Физический смысл величины γ заключается в том, что он показывает, во сколько раз изменяется скорость реакции при изменении температуры на каждые 10 градусов.

Поскольку скорость реакции и константа скорости химической реакции прямопропорциональны, то выражение (3.6) часто записывают в следующем виде:

(3.7)

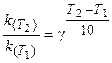
где k(T2), k(T1)- константы скорости реакции соответственно

при температурах T2 и T1;

Пример 8. На сколько градусов надо повысить температуру, что бы скорость реакции возросла в 27 раз? Температурный коэффициент реакции равен 3.

Решение. Используем выражение (3.6):

.

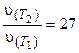
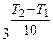
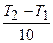
Получаем: 27 = , = 3, DТ = 30.

Ответ: на 30 градусов.

Скорость реакции и время, за которое она протекает, связаны обратно пропорциональной зависимостью: чем больше v, тем

меньше t. Математически это выражается соотношением

(3.8)

Пример 9. При температуре 293 К реакция протекает за 2 мин. За какое время будет протекать эта реакция при температуре 273 К, если γ = 2.

Решение. Из уравнения (3.8) следует:

.

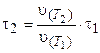
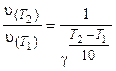
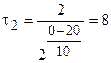
Используем уравнение (3.6), поскольку Получим:

мин.

Правило Вант-Гоффа применимо для ограниченного числа химических реакций. Влияние температуры на скорость процес-сов чаще определяют по уравнению Аррениуса.

Уравнение Аррениуса. В 1889 г. шведский ученый С. Арре-1иус на основании экспериментов вывел уравнение, которое на-звано его именем

, (3.9)

где k — константа скорости реакции;

k0 — предэксноненциальный множитель;

е — основание натурального логарифма;

Ea — постоянная, называемая энергией активации, определяемая природой реагентов:

R-универсальная газовая постоянная, равная 8,314 Дж/моль×К.

Значения Еa для химических реакций лежат в пределах 4 — 400 кДж/моль.

Многие реакции характеризуются определенным энергети-ческим барьером. Для его преодоления необходима энергия актации — некоторая избыточная энергия (по сравнению со вредней энергией молекул при данной температуре), которой должны обладать молекулы для того, чтобы их столкновение было эффективным, т. е. привело бы к образованию нового ве-щества. С ростом температуры число активных молекул быстро увеличивается, что и приводит к резкому возрастанию скорости реакции.

В общем случае, если температура реакции изменяется от Т1 до Т2, уравнение (3.9) после логарифмирования примет вид:

. (3.10)

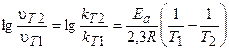
Это уравнение позволяет рассчитывать энергию активации реакции при изменении температуры от Т1 до Т2.

Скорость химических реакций возрастает в присутствии катализатора. Действие катализатора заключается в том, что он образует с реагентами неустойчивые промежуточные соединения (активированные комплексы), распад которых приводит к. образованию продуктов реакции. При этом энергия активации, понижается, и активными становятся молекулы, энергия которых была недостаточна для осуществления реакции в отсутствие, катализатора. В результате возрастает общее число активных£ молекул и увеличивается скорость реакции.

Изменение скорости реакции в присутствии катализатора выражается следующим уравнением:

, (3.11)

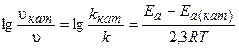
где vкат, и Ea(кат) — скорость и энергия активации химической реакции в присутствии катализатора;

v и Еа — скорость и энергия активации химической реакции без катализатора.

Пример 10. Энергия активации некоторой реакции в отсутствие катализатора равна 75,24 кДж/моль, с катализатором — 50,14 кДж/моль. Во сколько раз возрастает скорость реакции в присутствии катализатора, если реакция протекает при температуре 298 К? Решение. Воспользуемся уравнением (3.11). Подставляя в уравнение данные

Еа = 75,24 кДж / моль = 75,24 ×103 Дж / моль и

Еа(кат)=- 50,14 кД/моль= 50,14 ×103 Дж /моль, получим

Окончательно находим:

Таким образом, снижение энергии активации на 25,1 кДж/моль привело к увеличению скорости реакции в 25 000 раз.

Источник

Температурный коэффициент сопротивления

Температурный коэффициент сопротивления (ТКС) — величина, равная относительному изменению удельного сопротивления вещества при изменении температуры на единицу.

ТКС характеризует зависимость сопротивления проводника от изменении его температуры.Как правило применяют температурный коэффициент сопротивления металлов.

Формула температурного коэффициента сопротивления

Через относительное изменение сопротивления:

Через удельное сопротивление:

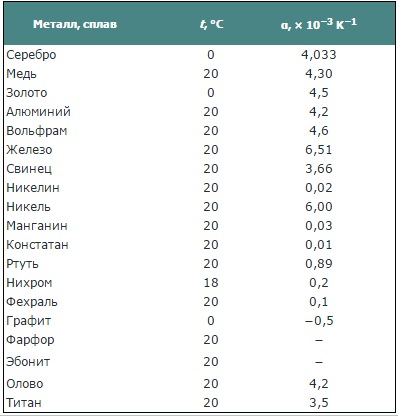
Таблица «Температурный коэффициент сопротивления»

Алюминий

температурный коэффициент сопротивления алюминия4,2

Вольфрам

температурный коэффициент сопротивления вольфрама5

Железо

температурный коэффициент сопротивления железа6

Золото

температурный коэффициент сопротивления золота4

Константан (сплав Ni-Cu + Mn)

температурный коэффициент сопротивления константина0,05

Латунь

температурный коэффициент сопротивления латуни0,1-0,4

Магний

температурный коэффициент сопротивления магния3,9

Манганин (сплав меди марганца и никеля — приборный)

температурный коэффициент сопротивления манганин0,01

Марганец

температурный коэффициент сопротивления марганца0,02

Медь

температурный коэффициент сопротивления меди4,3

Нейзильбер

температурный коэффициент сопротивления нейзильбера0,25

Никелин (сплав меди и никеля)

температурный коэффициент сопротивления никелина0,1

Никель

температурный коэффициент сопротивления никеля6,5

Нихром (сплав никеля хрома железы и марганца)

температурный коэффициент сопротивления нихрома0,1

Олово

температурный коэффициент сопротивления олова4,4

Платина

температурный коэффициент сопротивления платины3,9

Ртуть

температурный коэффициент сопротивления ртути1

Свинец

температурный коэффициент сопротивления свинца3,7

Серебро

температурный коэффициент сопротивления серебра4,1

Сталь

температурный коэффициент сопротивления стали1-4

Фехраль (Cr (12—15 %); Al (3,5—5,5 %); Si (1 %); Mn (0,7 %); + Fe)

Источник

Температурный коэффициент

СОДЕРЖАНИЕ

Отрицательный температурный коэффициент [ править ]

Большинство керамических материалов демонстрируют отрицательную температурную зависимость сопротивления. Этот эффект регулируется уравнением Аррениуса в широком диапазоне температур:

Следовательно, многие материалы, которые обеспечивают приемлемые значения, включают материалы, которые были легированы или обладают переменным отрицательным температурным коэффициентом (NTC), который возникает, когда физические свойства (такие как теплопроводность или удельное электрическое сопротивление ) материала снижаются с повышением температуры, обычно в определенный температурный диапазон. Для большинства материалов удельное электрическое сопротивление будет уменьшаться с повышением температуры. р 0 <\ displaystyle R_ <0>>

Обратимый температурный коэффициент [ править ]

Остаточная плотность магнитного потока или B _r изменяется в зависимости от температуры, и это одна из важных характеристик характеристик магнита. Для некоторых приложений, таких как инерционные гироскопы и лампы бегущей волны (ЛБВ), требуется постоянное поле в широком диапазоне температур. Коэффициент обратимой температуры (РКИ) из B _R определяются следующим образом:

RTC знак равно | Δ B р | | B р | Δ Т × 100 % <\ displaystyle <\ text > = <\ frac <| \ Delta \ mathbf _ |> <| \ mathbf _ | \ Delta T>> \ times 100 \ %>

Электрическое сопротивление [ править ]

α 0 = 1 ρ 0 [ δ ρ δ T ] T = T 0 <\displaystyle \alpha _<0>=<\frac <1><\rho _<0>>>\left[<\frac <\delta \rho ><\delta T>>\right]_>>

Однако в полупроводнике экспоненциально:

Это свойство используется в таких устройствах, как термисторы.

Положительный температурный коэффициент сопротивления [ править ]

Отрицательный температурный коэффициент сопротивления [ править ]

Отрицательный температурный коэффициент сопротивления полупроводника [ править ]

Повышение температуры полупроводникового материала приводит к увеличению концентрации носителей заряда. Это приводит к большему количеству носителей заряда, доступных для рекомбинации, что увеличивает проводимость полупроводника. Увеличение проводимости вызывает уменьшение удельного сопротивления полупроводникового материала с повышением температуры, что приводит к отрицательному температурному коэффициенту сопротивления.

Температурный коэффициент упругости [ править ]

Модуль упругости эластичных материалов изменяется с температурой, обычно снижаясь с повышением температуры.

Температурный коэффициент реактивности [ править ]

В ядерной технике температурный коэффициент реактивности является мерой изменения реактивности (приводящего к изменению мощности), вызванного изменением температуры компонентов реактора или теплоносителя реактора. Это можно определить как

Математический вывод аппроксимации температурного коэффициента [ править ]

В более общем виде дифференциальный закон температурных коэффициентов имеет вид:

Интегрируя дифференциальный закон температурных коэффициентов:

∫ R 0 R ( T ) d R R = ∫ T 0 T α d T ⇒ ln ⁡ ( R ) | R 0 R ( T ) = α ( T − T 0 ) ⇒ ln ⁡ ( R ( T ) R 0 ) = α ( T − T 0 ) ⇒ R ( T ) = R 0 e α ( T − T 0 ) <\displaystyle \int _>^<\frac >=\int _>^\alpha \,dT

R(T)=R_<0>e^<\alpha (T-T_<0>)>>

Применение приближения ряда Тейлора в первом порядке вблизи от приводит к: T 0 <\displaystyle T_<0>>

R ( T ) = R 0 ( 1 + α ( T − T 0 ) ) <\displaystyle R(T)=R_<0>(1+\alpha (T-T_<0>))>

Единицы [ править ]

Источник