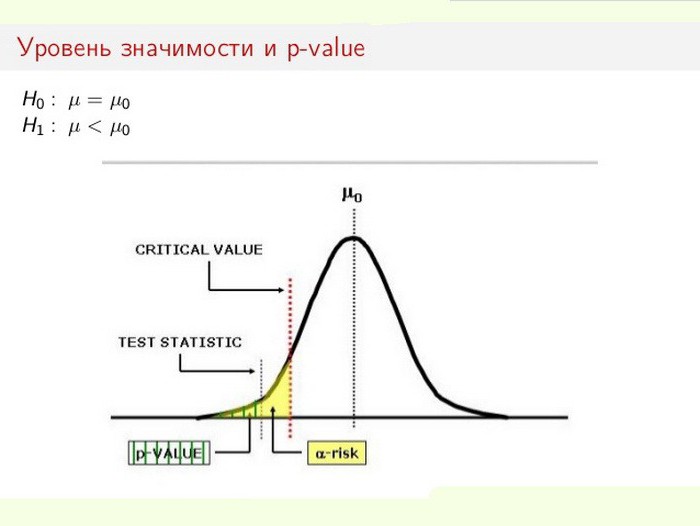
Что показывает уровень значимости альфа

Уровень значимости в статистике

Уровень значимости в статистике является важным показателем, отражающим степень уверенности в точности, истинности полученных (прогнозируемых) данных. Понятие широко применяется в различных сферах: от проведения социологических исследований, до статистического тестирования научных гипотез.

Определение

Уровень статистической значимости (или статистически значимый результат) показывает, какова вероятность случайного возникновения исследуемых показателей. Общая статистическая значимость явления выражается коэффициентом р-value (p-уровень). В любом эксперименте или наблюдении существует вероятность, что полученные данные возникли из-за ошибок выборки. Особенно это актуально для социологии.

То есть статистически значимой является величина, чья вероятность случайного возникновения крайне мала либо стремится к крайности. Крайностью в этом контексте считают степень отклонения статистики от нуль-гипотезы (гипотезы, которую проверяют на согласованность с полученными выборочными данными). В научной практике уровень значимости выбирается перед сбором данных и, как правило, его коэффициент составляет 0,05 (5 %). Для систем, где крайне важны точные значения, этот показатель может составлять 0,01 (1 %) и менее.

История вопроса

Понятие уровня значимости было введено британским статистиком и генетиком Рональдом Фишером в 1925 году, когда он разрабатывал методику проверки статистических гипотез. При анализе какого-либо процесса существует определенная вероятность тех либо иных явлений. Трудности возникают при работе с небольшими (либо не очевидными) процентами вероятностей, подпадающими под понятие «погрешность измерений».

При работе со статистическими данными, недостаточно конкретными, чтобы их проверить, ученые сталкивались с проблемой нулевой гипотезы, которая «мешает» оперировать малыми величинами. Фишер предложил для таких систем определить вероятность событий в 5 % (0,05) в качестве удобного выборочного среза, позволяющего отклонить нуль-гипотезу при расчетах.

Введение фиксированного коэффициента

В 1933 году ученые Ежи Нейман и Эгон Пирсон в своих работах рекомендовали заранее (до сбора данных) устанавливать определенный уровень значимости. Примеры использования этих правил хорошо видны во время проведения выборов. Предположим, есть два кандидата, один из которых очень популярен, а второй – малоизвестен. Очевидно, что первый кандидат выборы выиграет, а шансы второго стремятся к нулю. Стремятся – но не равны: всегда есть вероятность форс-мажорных обстоятельств, сенсационной информации, неожиданных решений, которые могут изменить прогнозируемые результаты выборов.

Нейман и Пирсон согласились, что предложенный Фишером уровень значимости 0,05 (обозначаемый символом α) наиболее удобен. Однако сам Фишер в 1956 году выступил против фиксации этого значения. Он считал, что уровень α должен устанавливаться в соответствии с конкретными обстоятельствами. Например, в физике частиц он составляет 0,01.

Значение p-уровня

Термин р-value впервые использован в работах Браунли в 1960 году. P-уровень (p-значение) является показателем, находящимся в обратной зависимости от истинности результатов. Наивысший коэффициент р-value соответствует наименьшему уровню доверия к произведенной выборке зависимости между переменными.

Данное значение отражает вероятность ошибок, связанных с интерпретацией результатов. Предположим, p-уровень = 0,05 (1/20). Он показывает пятипроцентную вероятность того, что найденная в выборке связь между переменными – всего лишь случайная особенность проведенной выборки. То есть, если эта зависимость отсутствует, то при многократных подобных экспериментах в среднем в каждом двадцатом исследовании можно ожидать такую ​​же либо большую зависимость между переменными. Часто p-уровень рассматривается в качестве «допустимой границы» уровня ошибок.

Кстати, р-value может не отражать реальную зависимость между переменными, а лишь показывает некое среднее значение в пределах допущений. В частности, окончательный анализ данных будет также зависеть от выбранных значений данного коэффициента. При p-уровне = 0,05 будут одни результаты, а при коэффициенте, равном 0,01, другие.

Проверка статистических гипотез

Уровень статистической значимости особенно важен при проверке выдвигаемых гипотез. Например, при расчетах двустороннего теста область отторжения разделяют поровну на обоих концах выборочного распределения (относительно нулевой координаты) и высчитывают истинность полученных данных.

Предположим, при мониторинге некоего процесса (явления) выяснилось, что новая статистическая информация свидетельствует о небольших изменениях относительно предыдущих значений. При этом расхождения в результатах малы, не очевидны, но важны для исследования. Перед специалистом встает дилемма: изменения реально происходят или это ошибки выборки (неточность измерений)?

Эффективность

Необходимо учитывать, что коэффициенты α и р-value не являются точными характеристиками. Каким бы ни был уровень значимости в статистике исследуемого явления, он не является безусловным основанием для принятия гипотезы. Например, чем меньше значение α, тем больше шанс, что устанавливаемая гипотеза значима. Однако существует риск ошибиться, что уменьшает статистическую мощность (значимость) исследования.

Исследователи, которые зацикливаются исключительно на статистически значимых результатах, могут получить ошибочные выводы. При этом перепроверить их работу затруднительно, так как ими применяются допущения (коими фактически и являются значения α и р-value). Поэтому рекомендуется всегда, наряду с вычислением статистической значимости, определять другой показатель – величину статистического эффекта. Величина эффекта – это количественная мера силы эффекта.

Источник

Уровень значимости и уровень надежности в EXCEL

history 23 ноября 2016 г.

Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в MS EXCEL .

СОВЕТ : Для понимания терминов Уровень значимости и Уровень надежности потребуется знание следующих понятий:

Уровень значимости обычно обозначают греческой буквой α ( альфа ). Чаще всего для уровня значимости используют значения 0,001; 0,01; 0,05; 0,10.

Уровень надежности

Термин Уровень надежности имеет синонимы: уровень доверия, коэффициент доверия, доверительный уровень и доверительная вероятность (англ. Confidence Level , Confidence Coefficient ).

В математической статистике обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д.

Например, Уровень доверия 95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор уровня доверия полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.

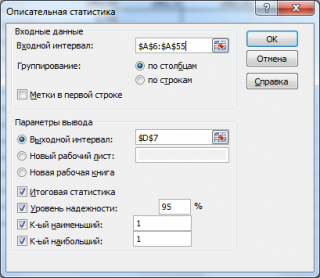
Уровень надежности в MS EXCEL

После нажатия кнопки ОК будет выведено другое диалоговое окно.

Если Уровень надежности задан 95%, то надстройка Пакет анализа использует следующую формулу (выводится не сама формула, а лишь ее результат):

или эквивалентную ей

где =СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) – является стандартной ошибкой среднего (формулы приведены в файле примера ).

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))

Источник

Выбор уровня значимости при проверке статистических гипотез

Проверка статистических гипотез основана на сравнении рассчитанного значения критерия с теоретическим значением, выбранного с заданным критическим уровнем значимости. От выбранного уровня значимости зависит результат проверки гипотез и сделанные исследователем выводы. Во многих учебниках и руководствах по использованию пакетов для статистического анализа приводится «магическое» значение 0,05, которое нужно выбирать в качестве критического уровня значимости. Можно ли всегда брать уровень значимости 0,05 или нет, попытаемся разобраться в этой статье.

Для начала кратко разберем основы проверки статистических гипотез. Статистической гипотезой будем называть любое предположение о законе распределения случайной величины или о параметрах этого закона. Это может быть предположение об отсутствии различий, об отсутствии взаимосвязи, о соответствии параметра заданному значению и т.д. Выделяют две виды гипотез: формулируемая гипотеза называется нулевой (основной) или гипотезой Н₀. Также обязательно формулируют альтернативную (конкурирующую) гипотезу Н₁. Предполагают, что либо верна гипотеза Н₀ при ложной гипотезе Н₁, либо вернаН₁ при ложной гипотезеН_0. Обе гипотезы одновременно быть ложными или истинными быть не могут.

Формулируют гипотезы таким образом, чтобы альтернативная гипотеза была «рабочей». Например, цель исследования доказать, что объем продаж увеличился на 10%. Тогда нулевая гипотеза будет сформулирована: объем продаж не увеличился. Цель проверки нулевой гипотезы будет заключаться в том, чтобы ее отвергнуть и доказать альтернативную гипотезу.

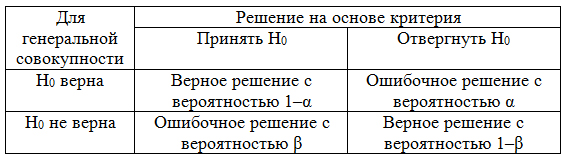
В зависимости от вида формулируемой нулевой гипотезы она может проверяться с помощью различных методов – статистических критериев. Статистический критерий – это некое правило, согласно которому нулевую гипотезу нужно принять или отвергнуть. Важно понимать, что при проверке гипотез мы работаем не с самой случайной величиной, а с данными выборки. Поэтому наши суждения на основе результатов проверки гипотез всегда имеют вероятностный характер. Какое бы решение мы не приняли, всегда существует ошибка принятия этого решения. Рассмотрим все возможные ошибки при принятии решений (см. таблицу).

Мы можем принять верную гипотезу Н₀ или отвергнуть не верную гипотезу Н₀ на основе критерия. В этом случае мы не совершаем никакой ошибки. А еще мы можем отвергнуть верную нулевую гипотезу – это называется ошибкой первого рода. Для оценки возможности совершения такой ошибки используют вероятность, обозначаемую α и называемую уровнем значимости критерия. Также возможна и ошибка второго рода β – когда мы принимаем неверную нулевую гипотезу. На практике может использоваться величина 1– β или мощность критерия – вероятность не совершить ошибку второго рода или принять неверную гипотезу.

Уровень значимости должен стремиться к нулю, а мощность критерия к 1. Эти два требования вступают в противоречие. Сделать равными нулю обе ошибки при проверке гипотез невозможно. С практической точки зрения обычно наиболее критической является ошибка первого рода, а не второго. И гипотеза Н₀ формулируется так, чтобы задача была ее отвергнуть и доказать истинность Н₁. В случае отвержения гипотезы нас интересует только ошибка первого рода. Поэтому критический уровень значимости задается исследователем, а уже мощность критерия можно посчитать по заданной вероятности ошибки первого рода. Исходя из заданного значения уровня значимости, берут теоретическое значение критерия по одной из таблиц распределения и сравнивают его с рассчитанным значением критерия. Именно в качестве такого критического значения предлагают брать уровень значимости 0,05.

В статистических пакетах обычно выдается не заданный нами уровень значимости, а накопленная вероятность наблюдения уровня статистического критерия (p-значение) при принятии нулевой гипотезы. Если p-величина меньше выбранного аналитиком критического уровня накопленной вероятности, то нулевая гипотеза отвергается. Чем меньше p-величина, тем меньше вероятность истинности нулевой гипотезы, тем сильнее основания отвергнуть нулевую гипотезу. Итак, выбор критического уровня имеет ключевое значение. Как же его выбрать?

При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости a. Однако при этом увеличивается вероятность ошибки второго рода b, т.е. снижается мощность критерия. Выбор уровня значимости требует компромисса между заданной значимостью и мощностью. Увеличивая уровень значимости, мы увеличиваем шансы отвергнуть нулевую гипотезу, что является нашей конечной целью, а с другой стороны мы также увеличиваем и вероятность ошибки первого рода.

При выборе критического уровня значимости необходимо обращать внимание на объем выборки. Общая идея тут следующая. При малом объеме выборки более вероятно получить случайный результат, например, получить различие в двух в выборках при их однородности. Следовательно, можно взять большую вероятность ошибки первого рода. При увеличении объема выборки случайные отклонения компенсируют друг друга, и получить значимое различие в выборках при их однородности менее вероятно. Следовательно, надо брать меньший уровень значимости. Стандартными уровнями значимости являются 0,1; 0,05; 0,01; 0,001. Поэтому нельзя всегда брать уровень значимость 0,05. Можно придерживаться следующих условных границ зависимости объема выборки от уровня значимости. Если объем выборки небольшой до 100 единиц, то можно вполне отвергнуть нулевую гипотезу при уровне значимости 0,05 или даже 0,1. При объеме выборки, измеряемой сотнями – от 100 до 1000, следует понизить уровень значимости хотя бы до 0,01. А при больших выборках, измеряемых тысячами наблюдений, уверенно отвергать нулевую гипотезу можно только при значимости меньшей 0,001.

Также при выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается важнее малого уровня значимости, и его значение выбирают относительно большим, например 0,1 или даже 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем последствия ошибок первого рода.

Кроме того, следует различать понятие статистической значимости и практической значимости. Заключение о практической значимости всегда делается исследователем, проверяющим гипотезу. И здесь истинными критерием является экспертное мнение исследователя, его опыт и интуиция, умение «чувствовать» истинный уровень значимости, а не применение стандартного значения 0,05. Окончательный выбор уровня значимости связан с риском, который наступает с выбором решения принимать или отвергать проверяемую гипотезу.

Источник

Объясняем p-значения для начинающих Data Scientist’ов

Я помню, когда я проходил свою первую зарубежную стажировку в CERN в качестве практиканта, большинство людей все еще говорили об открытии бозона Хиггса после подтверждения того, что он соответствует порогу «пять сигм» (что означает наличие p-значения 0,0000003).

Тогда я ничего не знал о p-значении, проверке гипотез или даже статистической значимости.

Я решил загуглить слово — «p-значение», и то, что я нашел в Википедии, заставило меня еще больше запутаться…

При проверке статистических гипотез p-значение или значение вероятности для данной статистической модели — это вероятность того, что при истинности нулевой гипотезы статистическая сводка (например, абсолютное значение выборочной средней разницы между двумя сравниваемыми группами) будет больше или равна фактическим наблюдаемым результатам.
— Wikipedia

Хорошая работа, Википедия.

Ладно. Я не понял, что на самом деле означает р-значение.

Углубившись в область науки о данных, я наконец начал понимать смысл p-значения и то, где его можно использовать как часть инструментов принятия решений в определенных экспериментах.

Поэтому я решил объяснить р-значение в этой статье, а также то, как его можно использовать при проверке гипотез, чтобы дать вам лучшее и интуитивное понимание р-значений.

Также мы не можем пропустить фундаментальное понимание других концепций и определение p-значения, я обещаю, что сделаю это объяснение интуитивно понятным, не подвергая вас всеми техническими терминами, с которыми я столкнулся.

Всего в этой статье четыре раздела, чтобы дать вам полную картину от построения проверки гипотезы до понимания р-значения и использования его в процессе принятия решений. Я настоятельно рекомендую вам пройтись по всем из них, чтобы получить подробное понимание р-значений:

1. Проверка гипотез

Прежде чем мы поговорим о том, что означает р-значение, давайте начнем с разбора проверки гипотез, где р-значение используется для определения статистической значимости наших результатов.

Наша конечная цель — определить статистическую значимость наших результатов.

И статистическая значимость построена на этих 3 простых идеях:

Другими словами, мы создадим утверждение (нулевая гипотеза) и используем пример данных, чтобы проверить, является ли утверждение действительным. Если утверждение не соответствует действительности, мы выберем альтернативную гипотезу. Все очень просто.

Чтобы узнать, является ли утверждение обоснованным или нет, мы будем использовать p-значение для взвешивания силы доказательств, чтобы увидеть, является ли оно статистически значимым. Если доказательства подтверждают альтернативную гипотезу, то мы отвергнем нулевую гипотезу и примем альтернативную гипотезу. Это будет объяснено в следующем разделе.

Давайте воспользуемся примером, чтобы сделать эту концепцию более ясной, и этот пример будет использоваться на протяжении всей этой статьи для других концепций.

Пример. Предположим, что в пиццерии заявлено, что время их доставки составляет в среднем 30 минут или меньше, но вы думаете, что оно больше чем заявленное. Таким образом, вы проводите проверку гипотезы и случайным образом выбираете время доставки для проверки утверждения:

Одним из распространенных способов проверки гипотез является использование Z-критерия. Здесь мы не будем вдаваться в подробности, так как хотим лучше понять, что происходит на поверхности, прежде чем погрузиться глубже.

2. Нормальное распределение

Нормальное распределение — это функция плотности вероятности, используемая для просмотра распределения данных.

Нормальное распределение имеет два параметра — среднее (μ) и стандартное отклонение, также называемое сигма (σ).

Среднее — это центральная тенденция распределения. Оно определяет местоположение пика для нормальных распределений. Стандартное отклонение — это мера изменчивости. Оно определяет, насколько далеко от среднего значения склонны падать значения.

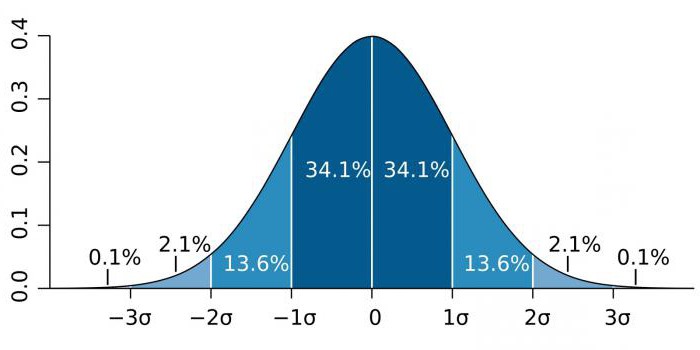
Нормальное распределение обычно связано с правилом 68-95-99.7 (изображение выше).

Классно. Теперь вы можете задаться вопросом: «Как нормальное распределение относится к нашей предыдущей проверке гипотез?»

Поскольку мы использовали Z-тест для проверки нашей гипотезы, нам нужно вычислить Z-баллы (которые будут использоваться в нашей тестовой статистике), которые представляют собой число стандартных отклонений от среднего значения точки данных. В нашем случае каждая точка данных — это время доставки пиццы, которое мы получили.

Обратите внимание, что когда мы рассчитали все Z-баллы для каждого времени доставки пиццы и построили стандартную кривую нормального распределения, как показано ниже, единица измерения на оси X изменится с минут на единицу стандартного отклонения, так как мы стандартизировали переменную, вычитая среднее и деля его на стандартное отклонение (см. формулу выше).

Изучение стандартной кривой нормального распределения полезно, потому что мы можем сравнить результаты теста с ”нормальной» популяцией со стандартизированной единицей в стандартном отклонении, особенно когда у нас есть переменная, которая поставляется с различными единицами.

Z-оценка может сказать нам, где лежат общие данные по сравнению со средней популяцией.

Мне нравится, как Уилл Кёрсен выразился: чем выше или ниже Z-показатель, тем менее вероятным будет случайный результат и тем более вероятным будет значимый результат.

Но насколько высокий (или низкий) показатель считается достаточно убедительным, чтобы количественно оценить, насколько значимы наши результаты?

Кульминация

Здесь нам нужен последний элемент для решения головоломки — p-значение, и проверить, являются ли наши результаты статистически значимыми на основе уровня значимости (также известного как альфа), который мы установили перед началом нашего эксперимента.

3. Что такое P-значение?

Наконец… Здесь мы говорим о р-значении!

Все предыдущие объяснения предназначены для того, чтобы подготовить почву и привести нас к этому P-значению. Нам нужен предыдущий контекст и шаги, чтобы понять это таинственное (на самом деле не столь таинственное) р-значение и то, как оно может привести к нашим решениям для проверки гипотезы.

Если вы зашли так далеко, продолжайте читать. Потому что этот раздел — самая захватывающая часть из всех!

Вместо того чтобы объяснять p-значения, используя определение, данное Википедией (извини Википедия), давайте объясним это в нашем контексте — время доставки пиццы!

Напомним, что мы произвольно отобрали некоторые сроки доставки пиццы, и цель состоит в том, чтобы проверить, превышает ли время доставки 30 минут. Если окончательные доказательства подтверждают утверждение пиццерии (среднее время доставки составляет 30 минут или меньше), то мы не будем отвергать нулевую гипотезу. В противном случае мы опровергаем нулевую гипотезу.

Поэтому задача p-значения — ответить на этот вопрос:

Если я живу в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), насколько неожиданными являются мои доказательства в реальной жизни?

Р-значение отвечает на этот вопрос числом — вероятностью.

Чем ниже значение p, тем более неожиданными являются доказательства, тем более нелепой выглядит наша нулевая гипотеза.

И что мы делаем, когда чувствуем себя нелепо с нашей нулевой гипотезой? Мы отвергаем ее и выбираем нашу альтернативную гипотезу.

Если р-значение ниже заданного уровня значимости (люди называют его альфа, я называю это порогом нелепости — не спрашивайте, почему, мне просто легче понять), тогда мы отвергаем нулевую гипотезу.

Теперь мы понимаем, что означает p-значение. Давайте применим это в нашем случае.

P-значение в расчете времени доставки пиццы

Теперь, когда мы собрали несколько выборочных данных о времени доставки, мы выполнили расчет и обнаружили, что среднее время доставки больше на 10 минут с p-значением 0,03.

Это означает, что в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), есть 3% шанс, что мы увидим, что среднее время доставки, по крайней мере, на 10 минут больше, из-за случайного шума.

Чем меньше p-значение, тем более значимым будет результат, потому что он с меньшей вероятностью будет вызван шумом.

В нашем случае большинство людей неправильно понимают р-значение:

Р-значение 0,03 означает, что есть 3% (вероятность в процентах), что результат обусловлен случайностью — что не соответствует действительности.

Р-значение ничего не *доказывает*. Это просто способ использовать неожиданность в качестве основы для принятия разумного решения.
— Кэсси Козырков

Вот как мы можем использовать p-значение 0,03, чтобы помочь нам принять разумное решение (ВАЖНО):

По моему мнению, p-значения используются в качестве инструмента для оспаривания нашего первоначального убеждения (нулевая гипотеза), когда результат является статистически значимым. В тот момент, когда мы чувствуем себя нелепо с нашим собственным убеждением (при условии, что р-значение показывает, что результат статистически значим), мы отбрасываем наше первоначальное убеждение (отвергаем нулевую гипотезу) и принимаем разумное решение.

4. Статистическая значимость

Наконец, это последний этап, когда мы собираем все вместе и проверяем, является ли результат статистически значимым.

Недостаточно иметь только р-значение, нам нужно установить порог (уровень значимости — альфа). Альфа всегда должна быть установлена ​​перед экспериментом, чтобы избежать смещения. Если наблюдаемое р-значение ниже, чем альфа, то мы заключаем, что результат является статистически значимым.

Основное правило — установить альфа равным 0,05 или 0,01 (опять же, значение зависит от вашей задачи).

Как упоминалось ранее, предположим, что мы установили альфа равным 0,05, прежде чем мы начали эксперимент, полученный результат является статистически значимым, поскольку р-значение 0,03 ниже, чем альфа.

Для справки ниже приведены основные этапы всего эксперимента:

Если вы хотите узнать больше о статистической значимости, не стесняйтесь посмотреть эту статью — Объяснение статистической значимости, написанная Уиллом Керсеном.

Последующие размышления

Здесь много чего нужно переваривать, не так ли?

Я не могу отрицать, что p-значения по своей сути сбивают с толку многих людей, и мне потребовалось довольно много времени, чтобы по-настоящему понять и оценить значение p-значений и то, как они могут быть применены в рамках нашего процесса принятия решений в качестве специалистов по данным.

Но не слишком полагайтесь на p-значения, поскольку они помогают только в небольшой части всего процесса принятия решений.

Я надеюсь, что мое объяснение p-значений стало интуитивно понятным и полезным в вашем понимании того, что в действительности означают p-значения и как их можно использовать при проверке ваших гипотез.

Сам по себе расчет р-значений прост. Трудная часть возникает, когда мы хотим интерпретировать p-значения в проверке гипотез. Надеюсь, что теперь трудная часть станет для вас немного легче.

Если вы хотите узнать больше о статистике, я настоятельно рекомендую вам прочитать эту книгу (которую я сейчас читаю!) — Практическая статистика для специалистов по данным, специально написанная для data scientists, чтобы разобраться с фундаментальными концепциями статистики.

Узнайте подробности, как получить востребованную профессию с нуля или Level Up по навыкам и зарплате, пройдя платные онлайн-курсы SkillFactory:

Источник