Что показывает ускорение при прямолинейном неравномерном движении
Содержание:
Прямолинейное неравномерное движение, ускорение:
На практике прямолинейное равномерное движение наблюдается очень редко. Скорость движущегося автомобиля, поезда, самолета, частей механизма и т.д. может изменяться и по величине, и по направлению.
Прямолинейное движение, при котором за равные промежутки времени материальная точка совершает разные перемещения, называют прямолинейным неравномерным движением.
При таком движении числовое значение скорости не остается неизменным, поэтому для описания неравномерного движения пользуются понятиями средней и мгновенной скорости.
Средняя скорость
Средняя скорость неравномерно движущейся материальной точки на данном участке траектории равна отношению ее перемещения на этом участке ко времени совершения этого перемещения:
Средняя путевая скорость материальной точки при неравномерном движении равна отношению всего пройденного пути ко времени, затраченному на прохождение этого пути:
Средняя скорость материальной точки, движущейся со скоростями 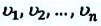
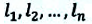
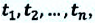
Если 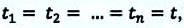
Мгновенная скорость.
Скорость материальной точки в данный момент времени или в данной точке траектории называют мгновенной скоростью.
Мгновенная скорость в некоторой точке является векторной величиной и определяется как предел отношения достаточно малого перемещения 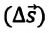
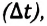
Где 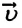
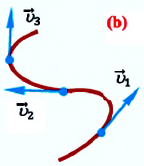
С течением времени мгновенная скорость может увеличиваться, уменьшаться и изменять направление. Направление мгновенной скорости в данной точке траектории совпадает с направлением касательной к траектории в этой точке (b). Проекция вектора мгновенной скорости в прямоугольной системе координат равна первой производной координаты по времени:
Ускорение
Быстрота изменения мгновенной скорости при неравномерном движении по величине и направлению характеризуется векторной физической величиной, называемой ускорением:
Если измерение времени начинается с нуля 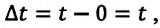
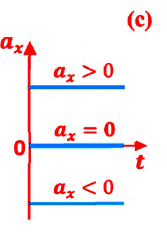
Направление ускорения совпадает с направлением вектора
Для простоты здесь и в последующем будет рассматриваться такое неравномерное прямолинейное движение материальной точки, при котором за любые равные промежутки времени происходит одинаковое изменение скорости. Такое движение называется равнопеременным движением.
Равнопеременное движение
При равнопеременном движении проекция ускорения на любую ось, например ось 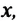
В СИ за единицу ускорения принят 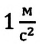
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Прямолинейное неравномерное движение. Движение по окружности



Основные положения:
Неравномерное движение– это движение с переменной скоростью.
Мгновенная скорость – это векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, стремящимся к нулю.
Если за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее скорости с течением времени изменяется. Такое движение называется неравномерным. В этом случае пользуются скалярной величиной, называемой средней путевой скоростью неравномерного движения на данном участке траектории. Она равна отношению пройденного пути к промежутку времени, за который этот путь пройден:
Средняя скорость при неравномерном движении – отношение вектора перемещения тела к промежутку времени, за который это перемещение произошло.
Для характеристики изменения скорости движения вводится понятие ускорения.
Средним ускорением неравномерного движения в интервале времени от t до 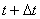
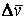
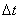
Мгновенным ускорением, или ускорением материальной точки в момент времени t, будет предел среднего ускорения:
Движение, происходящее с постоянным ускорением, называется равнопеременным.
Уравнение равнопеременного движения: 
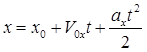
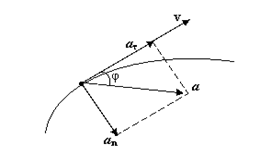
Вектор ускорения принято раскладывать на две составляющие: тангенциальное и центростремительное ускорение.
Тангенциальное ускорение показывает быстроту изменения модуля скорости, а нормальное ускорение характеризует быстроту изменения направления скорости при криволинейном движении.
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:
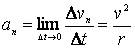
Контрольные вопросы:
1. Дать определение неравномерного движения.
2. Что называют равнопеременным движением?
3. Дайте определение мгновенной скорости.
4. Как направлен вектор мгновенной скорости?
5. Дайте определение мгновенного ускорения. В каких единицах измеряется?
6. Как направлены тангенциальное и центростремительное ускорение относительно кривизны траектории?
7. Дайте определение угловой скорости. Ее единицы измерения.
Выполните задания:
1. Напишите формулы зависимости:
а) частоты вращения от периода;
б) угловой скорости от периода;
в) угловой и линейной скорости;
г) угловой скорости от частоты;
д) центростремительного ускорения от скорости;
е) линейной скорости от частоты вращения;
ж) линейной скорости от периода.
2. Заполните таблицу:
| Характеристика движения | Тип величины | Формулы для прямолинейного равнопеременного движения |
| Перемещение | ||
| Скорость | ||
| Ускорение | ||
| Координата |
1. Тело, двигаясь из состояния покоя, прошло путь S1 = 150 м за время t1 = 3 c. На каком расстоянии S2 оно находилось через t2 = 4 с после начала пути?
2. При равноускоренном движении из состояния покоя тело проходит за пятую секунду 40 см. Определить перемещение тела за седьмую секунду.
3. Колесо велосипедиста имеет радиус 0,38 м. С какой скоростью движется велосипед, если колесо делает 90 оборотов в минуту? Какова угловая скорость вращения колеса при этом движении?
Задания для самостоятельной работы:
1. С крыши капают капли. На сколько перемещение капли в секунду t1меньше ее перемещения в секунду t2?
| Вариант |
| t1, c |
| t2, c |
2. Дискобол раскручивает диск, делая n оборотов в минуту. Оцените угловую скорость раскрутки и линейную скорость полета, считая расстояние от края диска до центра вращения равным R.
Неравномерное движение: ускорение
Если за равные промежутки времени перемещение тела различно, то движение будет неравномерным.
Движение может быть равноускоренным – это такое движение, при котором скорость меняется на одинаковое значение за единицу времени.
Равноускоренное движение можно наблюдать у разгоняющегося самолёта, у падающего камня, у машины с зажатыми тормозами (т.к. равнозамедленное движение тоже формально называется равноускоренным).
Ускорение – это физическая величина, обозначающая, на сколько меняется скорость тела за единицу времени. Ускорение – это векторная величина, не скалярная. Ускорение обозначается латинской буквой «a» и рассчитывается по формуле:
Для решения задач находим проекцию вектора ускорения на координатную ось:
Измеряется как м/с 2 (метр деленный на секунду в квадрате).
Так как ускорение величина векторная, то нужно знать, куда оно направлено:
— если тело разгоняется, то ускорение направлено туда же, куда и скорость;
— если тело тормозит, то ускорение направлено противоположно вектору скорости.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
При правильном ответе Вы получите 1 балл
Новая машина агента 007 разгоняется до 108 км/ч за 3 секунды. С каким ускорением происходит разгон? (в ответах м/с2 = м/с 2 )
Выберите всего один правильный ответ.
При правильном ответе Вы получите 1 балл
Новая машина агента 007 едва не врезалась в препятствие. Агент 007 заметил, что до торможения скорость была 108 км/ч, а после – 0 км/ч. Кроме того, он отчётливо помнит, что испытывал перегрузку в 1.5g (15 м/с 2 ).
За какое время машина остановилась?
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Что показывает ускорение при прямолинейном неравномерном движении
При неравномерном движении тело может за равные промежутки времени проходить как равные, так и разные пути.
|
Средняя скорость, по данному определению, величина скалярная потому, что путь и время величины скалярные.
Однако среднюю скорость можно определять и через перемещение согласно уравнению
В этом случае среднюю скорость следует считать величиной векторной потому, что она определяется через отношение векторной величины к скалярной.
Средняя скорость прохождения пути и средняя скорость перемещения – это две разные величины, которые могут характеризовать одно и то же движение.
При расчете средней скорости очень часто допускается ошибка, состоящая в том, что понятие средней скорости подменяется понятием среднего арифметического скоростей тела на разных участках движения. Чтобы показать неправомерность такой подмены рассмотрим задачу и проанализируем ее решение.
Из пункта в пункт выходит поезд. Половину всего пути поезд движется со скоростью 30 км/ч, а вторую половину пути – со скоростью 50 км/ч.
Движение поезда на участке и на участке равномерное. Взглянув на текст задачи, нередко сразу хочется дать ответ: υср = 40 км/ч.
Да потому, что нам кажется, что для вычисления средней скорости вполне подходит формула, используемая для расчета среднего арифметического.
Давайте разберемся: можно ли использовать эту формулу и рассчитывать среднюю скорость путем нахождения полусуммы заданных скоростей.
Для этого рассмотрим несколько иную ситуацию.
Допустим, мы правы и средняя скорость действительно равна 40 км/ч.
Тогда решим другую задачу.
Из пункта в пункт выходит поезд. Половину всего времени (до точки ) он движется со скоростью 30 км/ч, а вторую половину времени – со скоростью 50 км/ч.
Как видно, тексты задач очень похожи, есть только «очень маленькая» разница.
Если в первом случае речь идет о половине пути, то во втором случае речь идет о половине времени.
Если мы, решая вторую задачу, так же дадим ответ, что средняя скорость равна полусумме скоростей на первом и втором участке, мы не можем быть уверены, что мы решили задачу правильно. Как быть?
Начинать решение задачи нужно именно с формулы, определяющей среднюю скорость, даже если нам кажется, что мы в каком-то случае можем использовать более простую формулу.
Будем двигаться от вопроса к известным величинам.
Неизвестную величину υср выражаем через другие величины – 0 и Δ0.
Подставим эти величины, соответственно, в числитель и знаменатель исходного уравнения.
Во втором случае мы поступаем точно так же. Нам не известен весь путь и все время. Выражаем их: 
Очевидно, что время движения на участке во втором случае и время движения на участке в первом случае различны.
В первом случае, поскольку нам неизвестны времена 





Подставляем выраженные величины в исходные уравнения.
Таким образом, в первой задаче имеем:
После преобразования получаем:
Во втором случае получаем 
Ответы, как и было предсказано, различны, но во втором случае мы получили, что средняя скорость действительно равняется полусумме скоростей.
Может возникнуть вопрос, а почему сразу нельзя воспользоваться этим уравнением и дать такой ответ?
При неравномерном движении скорость тела может непрерывно меняться. При таком движении скорость в любой последующей точке траектории будет отличаться от скорости в предыдущей точке.
Чем больше промежуток времени Δ, тем средняя скорость больше отличается от мгновенной. И, наоборот, чем меньше промежуток времени, тем меньше средняя скорость отличается от интересующей нас мгновенной скорости.
Определим мгновенную скорость как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени :
Если речь идет о средней скорости перемещения, то мгновенная скорость является величиной векторной:
Если речь идет о средней скорости прохождения пути, то мгновенная скорость является величиной скалярной:
Часто встречаются случаи, когда при неравномерном движении скорость тела меняется за равные промежутки времени на одну и ту же величину.
При равнопеременном движении скорость тела может, как уменьшаться, так и увеличиваться.
Если скорость тела увеличивается, то движение называется равноускоренным, а если уменьшается – равнозамедленным.
Ускорение – это векторная физическая величина, равная отношению изменения скорости тела ко времени, в течение которого это изменение произошло:
Ускорение при равнопеременном движении не зависит ни от изменения скорости, ни от времени изменения скорости.
Ускорение показывает, на сколько изменяется скорость тела за единицу времени.
Зная ускорение тела и его начальную скорость, можно найти скорость в любой наперед заданный момент времени:
В проекции на координатную ось уравнение примет вид: υ = υ0 + ∙ Δ.
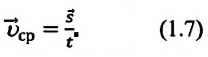
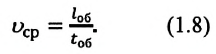
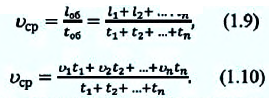
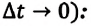
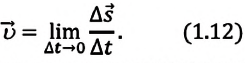
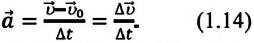
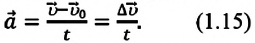
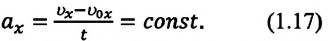
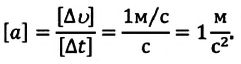



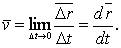
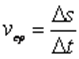
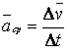
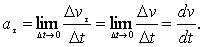
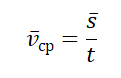
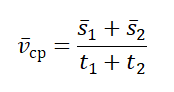
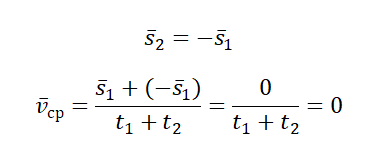
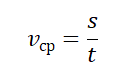
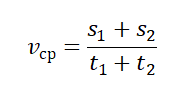
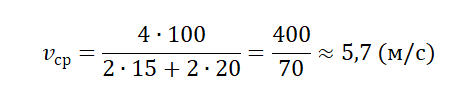
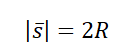
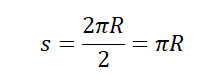
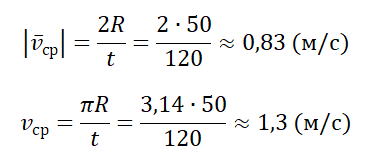
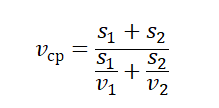
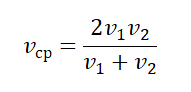
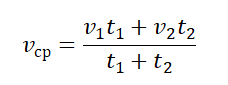
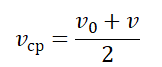
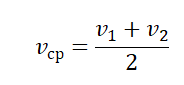
 где – весь путь, а – все время движения на рассматриваемом участке.
где – весь путь, а – все время движения на рассматриваемом участке.










