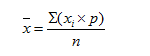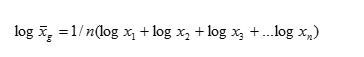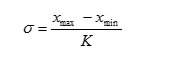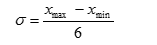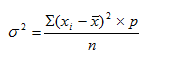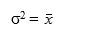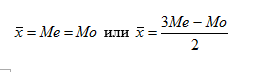Что показывает вариационный ряд
Вариационный ряд и методика его составления



Средние величины рассчитываются на основе вариационных рядов.
Вариационный ряд — это однородная в качественном отношении статистическая совокупность, отдельные единицы которой характеризуют количественные различия изучаемого признака или явления.
Цифровое значение, каждого отдельного признака или явления, входящего в вариационный ряд, называется вариантой и обозначается буквой V. Числа, показывающие, как часто встречается та или иная варианта в составе данного ряда, носят названия частот и обозначаются буквой — р. Общее число случаев наблюдений, из которых вариационный ряд состоит, обозначают буквой n.
Варианты, расположенные в порядке возрастания или убывания количественной характеристики признака, составляют ранжированный вариационный ряд.
| Вариационный ряд | |||||
| I Виды вариационных рядов | Простой | Сгруппированный | |||
| II Характеристика вариационного ряда | Варианта V | Частота p | Общее число наблюдений n | ||
| III Этапы составления сгруппированного ряда | Определение числа групп | Определение интервала | Определение границ и середины группы | Распределение наблюдений по группам | Графическое изображение |
| IV Практическое применение | Для характеристики типа распределения признака в совокупности | Для вычисления среднего уровня (средней величины) |
Различают два вида вариационных рядов:
— простой вариационный ряд;
— сгруппированный вариационный ряд,
Простым вариационным рядом называется такой ряд, где каждая варианта встречается лишь один раз. Вариационный ряд, где указано сколько раз встречается каждая варианта называется сгруппированным вариационным рядом.
Если исследователь имеет не более 30 наблюдений, то достаточно все значения признака расположить в нарастающем или в убывающем порядке (от минимальной варианты до максимальной или наоборот) и указать частоту каждой варианты. При большом числе наблюдений (более 30) рекомендуется варианты объединить в группы с указанием частоты встречаемости всех вариант, входящих в данную группу.
Основные требования к составлению вариационного ряда:
1. Расположить все варианты по порядку
2. Суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой единицы
3. Определить количество групп
4. Определить интервал между группами
5. Определить начало, середину и конец группы
6. Распределить данные наблюдений по группам
7. Графические изобразить вариационный ряд
Методику построения сгруппированного вариационного ряда рассмотрим на следующем примере:
Даны данные о частоте пульса (число ударов в минуту) у 54 студентов перед экзаменом: 60, 70, 70, 68, 70, 72, 64, 66, 66, 70, 76, 76, 80, 64, 6.2, 78, 78, 76, 70, 68, 64, 62, 70, 68, 72, 70, 72, 72, 70, 70, 76, 76, 76 74, 74, 74, 80, 80, 66, 72, 76, 76, 74, 74, 74, 72, 78, 78, 76, 74, 76, 76, 80, 78.
1. Строим вариационный ряд, последовательно располагая варианты в порядке возрастания: 60, 62, 62, 64, 64, 64, 66, 66, 66, 68, 68, 68, 70, 70, 70, 70, 70, 70, 70, 70, 70, 72, 72, 72, 72, 72, 72,74, 74, 74, 74, 74, 74, 74,76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 78, 78, 78, 78, 78, 80, 80, 80, 80.
2. Распределение студентов в зависимости от частоты пульса перед экзаменом
| частота пульса (V) |
| число студентов (p) |
Всего студентов n =54
3. Определение количества групп.
Количество групп в вариационном ряду находим в специально разработанной таблице.
| Число вариант (n) | 31–45 | 46–101 | 101–200 | 201–500 |
| Число групп (р) | 6–7 | 8–10 | 11–12 | 13–17 |
В нашем примере число наблюдений — 54, поэтому в вариационном ряду следует иметь 8 групп.
3. Определение величины интервала (i) между группами. Интервал между группами определяют по формуле:
| i= | Vmax–Vmin | = | 80–60 | = | =2,5 |
| r (число групп) |
Полученный интервал 2,5 рекомендуется округлять до целого числа — 3.
6. Разбиваем весь ряд на группы используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда
| частота пульса (V) | середина группы вариант | число студентов |
| 60–62 | ||
| 63–65 | ||
| 66–68 | ||
| 69–71 | ||
| 72–74 | ||
| 75–77 | ||
| 78–80 | ||
| n = 54 |
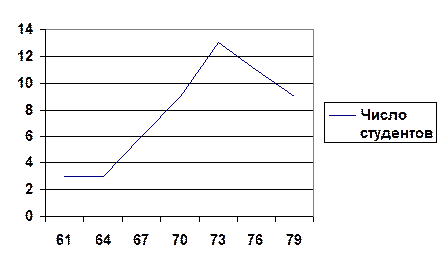
7. Строим графическое изображение вариационного ряда (по серединам групп)
Распределение студентов по частоте пульса перед экзаменом
Полученный ряд распределения (вариационный ряд) и графическое его изображение делают статистические данные обозримыми, доступными для анализа и дальнейшего изучения.
Вариационные ряды — помощь в оценке распределения явлений по величине признаков
Вариационный ряд (frequency table)- ранжированный ряд распределения по величине какого-либо признака. Этот признак носит название варьирующего, а его отдельные числовые значения называются вариантами и обозначаются через «х». Число, показывающее, сколько раз данная варианта встречается в вариационном ряду, называется частотой и обозначается через «р».
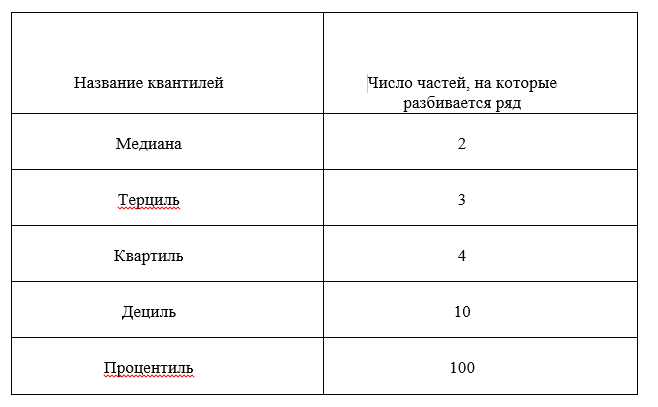
Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями (quantile). Наиболее часто употребляемые квантили представлены в таблице:
Рис. 1 Этапы описания (обобщения) количественного признака
Виды вариационных рядов
Вариационные ряды могут быть следующих видов:
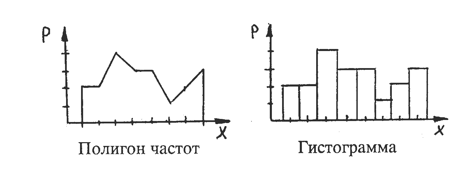
Графическое изображение вариационных рядов
где х — варианты, р — частоты.
Основные характеристики вариационного ряда
Такие характеристики зависят от оцениваемых показателей:
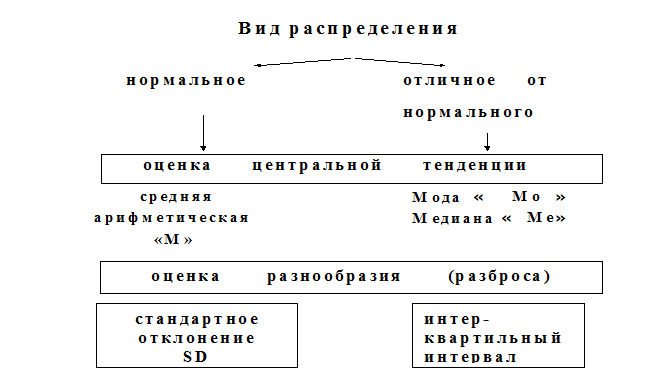
1). Показатели, характеризующие центральную тенденцию (central tendency) или уровень ряда: средние величины или меры расположения (собственно средние и структурные средние).
2). Показатели, характеризующие разнообразие (рассеяние, вариацию, разброс) (spread) признака: стандартное отклонение, дисперсия, размах, интерквартильный интервал.
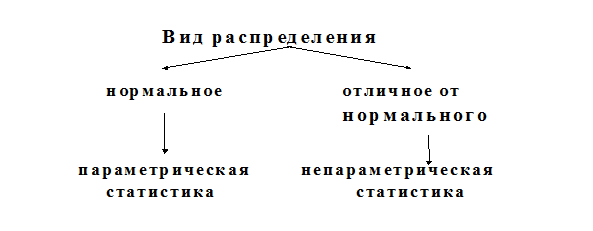
Выбор характеристик центральной тенденции и разнообразия признака прежде всего зависит от вида распределения. В случае нормального распределения используют показатели параметрической статистики, в случае распределения, отличного от нормального и при неизвестном виде распределения применяют показатели непараметрической статистики.
Средние величины
Средняя величина — обобщающий коэффициент, который характеризует наиболее типичный размер определенного признака в целом для совокупности или для отдельных ее частей. Расчет средних величин имеет смысл только для качественно однородной совокупности, в связи с этим в одной совокупности может быть столько средних, на сколько однородных групп она может быть разбита.
Виды средних величин
Средняя арифметическая(mean) — применяется, если варианты возрастают (убывают) в арифметической прогрессии.
х — средняя арифметическая;
р — частота встречаемости варианты;
n — число наблюдений
Свойства средней арифметической:
— носит обобщающий характер;
— имеет абстрактное значение;
— алгебраическая сумма отклонений отдельных вариант от средней равна 0 (сущность средней и способ проверки правильности расчета средней);
— сумма квадратов отклонений отдельных вариант от средней меньше суммы квадратов отклонений вариант от любой другой величины, неравной средней;
— сумма произведений отдельных вариант на свои частоты равна произведению средней на число наблюдений (единство суммарного действия и способ проверки правильности расчета средней);
— если частоту всех вариант пропорционально изменить, то средняя арифметическая от этого не изменится.
Средняя геометрическая — вычисляется, если варианты возрастают (убывают) в геометрической прогрессии.
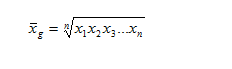
Структурные средние
Мода (Мо) (mode)- наиболее часто встречающаяся в вариационном ряду варианта.
Медиана (Me)(median) — варианта, которая делит вариационный ряд на две равные
части. Медиана используется:
Характеристики разнообразия вариационного ряда
— приблизительный расчет стандартного отклонения по амплитуде:
где К — коэффициент Ермолаева, рассчитывается по специальной таблице с учетом числа наблюдений (см. приложение).
При числе наблюдений больше 30:
Стандартное отклонение наиболее часто используется при определении нормы и патологии, в основе которого лежит «правило трех сигм», справедливое только для нормального распределения.
Сводная таблица формул
для нахождения средних значений и мер рассеяния
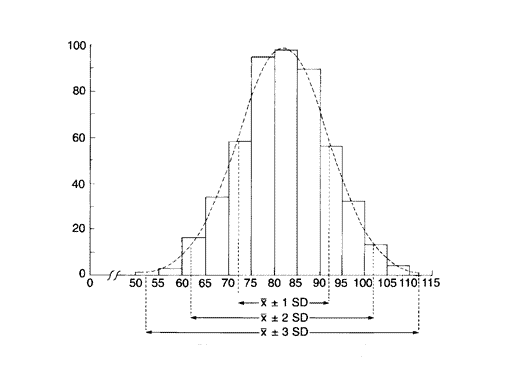
«Правило трех сигм»
68.3 % всех вариант отклоняются от своей средней не более, чем на s
95.4% вариант находятся в пределах X ± 2s
99.7% вариант находятся в пределах X ± 3s
Отклонение параметра от его средней арифметической в пределах s расценивается как норма, субнормальным считается отклонение в пределах ± 2s и патологическим — сверх этого предела, т.е. > ± 2s» (рис. )
Рис.3 Правило «трех сигм» ( SD – стандартное отклонение).
При распределении Пуассона дисперсия равна средней:
Коэффициент вариации используется при сравнении вариационных рядов, имеющих различную размерность, или одной размерности, но обладающими резкими различиями в своих значениях, затрудняющими их сопоставление.
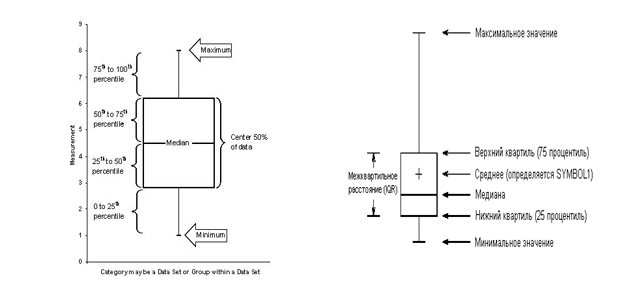
Вариационный ряд разбивают на четыре интервала, получая, соответственно, 25%, 50% и 75% квантили; 25% и 75% квантили называют также нижним (low quartile) и верхним квартилями(high quartile). 50% квантиль – это медиана. Внутри интерквартильного интервала (между 25% и 75% квантилями) лежат 50% наиболее типичных (близких к центральному) значений.
Таким образом, в случае нормального распределения вариационный ряд описывается средней величиной и стандартным отклонением, если распределение неизвестно или оно отлично от нормального, центральную тенденцию и разброс можно описать с помощью медианы, нижнего и верхнего квартиля (интерквартильным интервалом).
Рис.4 Графическое представление описательной статистики (коробчатый график, «коробка с усами», box-plot)
Проверка нормальности распределения
Соответствие экспериментального распределения нормальному проверяется следующими способами:
х ± 0.3 s находится 25 % всех единиц наблюдения;
х ± 0.7 s находится 50 % всех единиц наблюдения;
х ± l,l s находится 75 % всех единиц наблюдения;
х ± 3,0 s находится 99 % всех единиц наблюдения.
— при нормальном распределении, которое обладает симметричностью:
— правило «двух третей» Юла:
а). если распределение симметрично: Me = Mo;
б). если распределение обладает правосторонней асимметрией: Me > Mo;
в). если распределение имеет левостороннюю асимметрией Me 0
в) при левосторонней асимметрии: A s s × f, то «выскакивающая» варианта исключается из исследования;
Вариационные ряды
| Главная > Учебные материалы > Математика: Вариационные ряды | ||
 | ||
 | ||
| 1.Вариационный ряд. 2.Числовые характеристики вариационного ряда. |
1.Вариационный ряд.
Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.

Таб.1
По данным таблицы построим полигон распределения частот (рис.1)
В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.

Таб. 2
По данным таблицы построим гистограмму распределения частот (рис.2)
Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.
2.Числовые характеристики вариационного ряда.
Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости.
Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической.
Дисперсией s 2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической.
Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии.
Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака.
Пример.
В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины.
Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен.
Как видно из таблицы сумма произведений x i n i = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда.

По данным таблицы построим гистограмму распределения частот.

Построим и эмпирическую функцию распределения случайной величины (кумуляту).


Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:
Что показывает вариационный ряд
В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.
Это обстоятельство приводит к мысли построить статистические характеристики:
Пример 156. Имеются данные о количестве студентов в 30 группах физико-математического факультета:
| 26 | 25 | 25 | 26 | 25 | 23 |
| 23 | 24 | 19 | 23 | 20 | 19 |
| 22 | 24 | 24 | 23 | 20 | 23 |
| 24 | 19 | 21 | 18 | 21 | 18 |
| 20 | 18 | 18 | 21 | 15 | 15 |
Найти вариационный ряд количества студентов в группах и размах варьирования. Построить полигон частот.
Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:
| 15 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 2 | 4 | 2 | 4 | 3 | 1 | 5 | 4 | 3 | 2 |
Для построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты и полученные точки соединим отрезками.
Пример 157. Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающие числа. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
| Кол-во баллов | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Кол-во школьников | 2 | 3 | 2 | 4 | 12 | 10 | 8 | 9 |
Составить статистическое распределение количества школьников по количеству набранных баллов и построить полигон относительных частот.
Решение. Пусть = <количество набранных баллов>, a = <относительные частоты>. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
| X | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 0,04 | 0,06 | 0,04 | 0,08 | 0,24 | 0,2 | 0,16 | 0,18 |
Пример 158. В 2002 году количество служб, представляющих гражданам жилищные субсидии, по сельским районам области распределено следующим образом:
Построить эмпирическую функцию распределения.
Решение. Найдем сначала статистический ряд распределения числа служб в районах области.
Эмпирическую функцию распределения находим аналогично интегральной функции (см. §13 ) [перейти].
Пример 159. Построить гистограмму следующей выборки объема 50
Решение. Найдем плотность относительной частоты для каждого интервала и заполним последний столбец таблицы:
Из способа построения гистограммы следует, что полная ее площадь равна единице.
Построить гистограмму распределения числа школ по районам области.
Решение. Выберем границы интервалов и составим по данной выборке следующую таблицу
Аналогично предыдущему примеру строим гистограмму числа школ, распределенных по малым городам и районам области.
«Сглаживая» полученную гистограмму, получаем «похожесть» данного дискретного закона распределения на классический показательный (непрерывный) закон. В этом и заключается основное предназначение гистограмм выборок.
Вопросы для самоконтроля
На каких методах основано изучение статистических данных?
Основные задачи математической статистики.
Какие способы отбора из генеральной совокупности вы знаете?
Какая выборка называется представительной?
В чем отличие вариационного от статистического ряда?
Для чего используется полигон частот?
Свойства эмпирической функции распределения.
В каком случае и для чего строятся гистограммы?
I. 311. Записать выборку 2, 7, 3, 5, 4, 10, 5, 5, 2, 8, 10, 2, 7, 7, 7, 5, 4, 2, 4, 7, 8 в виде: а) вариационного ряда; б) статистического ряда.
312. Найдите эмпирическую функцию распределения для выборки, представленной вариационным рядом:
| 1 | 2 | 4 | 7 |
| 10 | 20 | 30 | 40 |
313. Имеются данные о количестве сельских населенных пунктов районов Ярославской области с численностью населения более 500 человек:
Найдите вариационный ряд количества населенных пунктов Ярославской области с численностью населения более 500 человек. Постройте полигон частот.
314. В 2002 году количество крупных и средних промышленных предприятий по районам ( в том же порядке, что и в предыдущей задаче) области распределено следующим образом:
Постройте полигон частот и эмпирическую функцию распределения.
315. Количество учащихся, получивших аттестат с медалью, в 2001 году по городам и районам Ярославской области:
Найдите вариационный ряд распределения медалистов, размах варьирования и среднее число медалистов по городам и районам области.
316. Посевные площади картофеля (тыс. гектаров) в сельских хозяйствах Ярославской области по районам:
1,5; 1,5; 0,6; 1,3; 0,9; 0,9; 0,6; 1,3; 1,1; 0,6; 1,1; 0,9; 1,6; 1,3; 0,8; 0,4; 1,1.
Найдите статистический ряд распределения посевных площадей и постройте полигон относительных частот.
—
- Что показывает валюта баланса предприятия
- Что показывает ваттметр включенный в первичную цепь трансформатора если вторичная цепь разомкнута