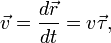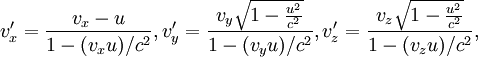Что показывает вектор скорости

Вектор скорости

Ско́рость (часто обозначается 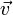, от англ. velocity или фр. vitesse ) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Содержание

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора 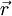этой точки:

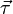
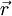
Здесь v — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Преобразование скорости

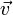
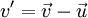
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношение между единицами скорости

См. также

Полезное

Смотреть что такое «Вектор скорости» в других словарях:

вектор скорости — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN velocity vector … Справочник технического переводчика

вектор скорости — greičio vektorius statusas T sritis fizika atitikmenys: angl. velocity vector vok. Geschwindigkeitsvektor, m rus. вектор скорости, m pranc. vecteur de vitesse, m; vecteur vitesse, m … Fizikos terminų žodynas

вектор скорости — greičio vektorius statusas T sritis Kūno kultūra ir sportas apibrėžtis Dydis, rodantis greičio statinę vertę (reikšmę) ir taško judėjimo kryptį. atitikmenys: angl. vector of velocity vok. Vektor der Geschwindigkeit, m rus. вектор скорости … Sporto terminų žodynas

вектор скорости ветра — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN wind vectorU … Справочник технического переводчика

вектор скорости вибрации — 3.4 вектор скорости вибрации : Вектор, содержащий шесть составляющих скорости вибрации (три линейные и три поворотные), направленных вдоль координатных осей x, y и z. Источник … Словарь-справочник терминов нормативно-технической документации

вектор скорости вибрации n-го виброизолятора — 3.13 вектор скорости вибрации n го виброизолятора : Вектор скорости вибрации n го виброизолятора (матрица столбец), содержащий шесть составляющих (три линейные и три поворотные), направленных вдоль координатных осей x, y и z. Источник … Словарь-справочник терминов нормативно-технической документации

вектор скорости вибрации в n-й точке — 3.6 вектор скорости вибрации в n й точке : Вектор в n й точке (матрица столбец), содержащий три линейные составляющие скорости вибрации, направленные вдоль координатных осей х, у и z соответственно. Источник … Словарь-справочник терминов нормативно-технической документации

вектор — 01.03.02 вектор [ vector] (1)1): Величина, представляемая значением, направлением, смысловым содержанием и началом. 1)Терминологические статьи 01.03.02 и 01.03.03 относятся к одному понятию. Источник … Словарь-справочник терминов нормативно-технической документации

ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера

Источник

Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений

Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.

Что такое скорость и ускорение?

Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Вам будет интересно: Дистанционное образование в России: история, статистика и преимущества

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:

Здесь вектор l¯ направлен от начальной точки пути к конечной.

В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:

Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.

Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.

Куда направлены векторы ускорения и скорости?

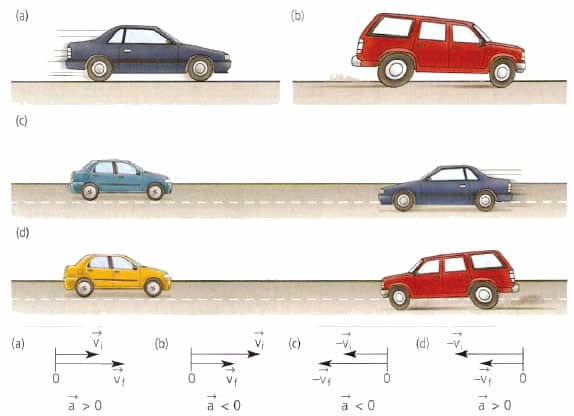
Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.

Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.

Действующая на тело сила и ускорение

Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.

Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:

Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.

Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.

Движение по окружности и ускорение

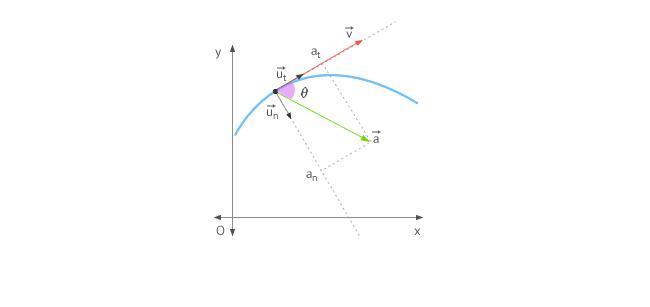
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.

Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.

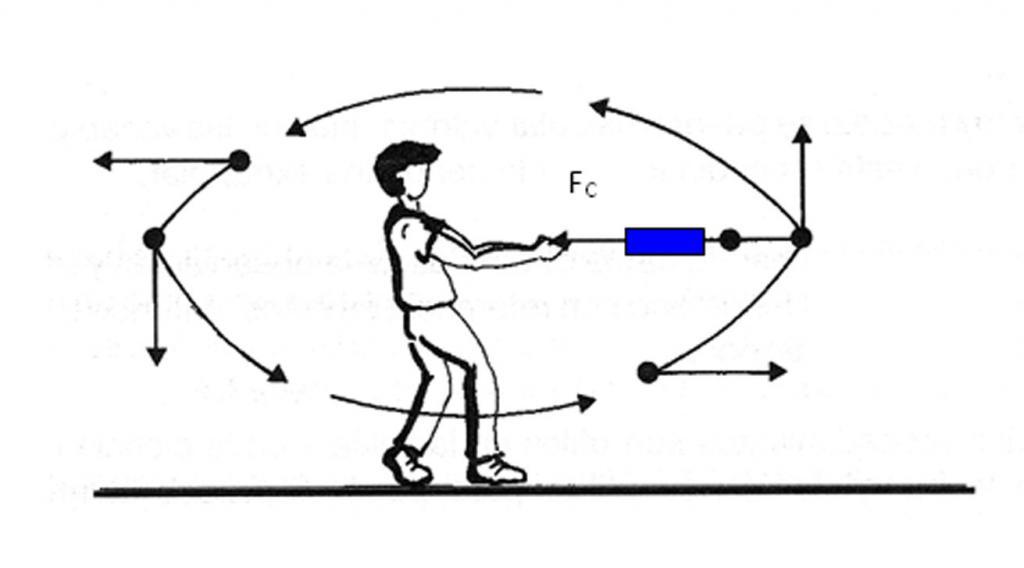
Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.

Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.

Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.

Источник

Основы механики для чайников. Часть 1: Кинематика

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Источник

Вульгаризмы в механике: о вредности термина «замедление»

Довольно часто, особенно в обиходе инженерных дисциплин, употребляется понятие «замедление» то есть ускорение, действие которого приводит к уменьшению модуля скорости. При этом такому ускорению приписывается некий отрицательный знак, подчеркивающий этот самый замедляющий эффект.

По моему скромному мнению данное понятие является не только избыточным, но и вредным с методической точки зрения. Оно бросает своего рода мутную вуаль на суть величин, описывающих механическое движение.

На самом деле, чтобы описать то же торможение автомобиля или парашютиста совершенно необязательно приписывать ускорению знак, достаточно понимания, что ускорение есть величина векторная и умения грамотно переходить от операций с векторами к операциям с их проекциями на оси выбранной системы координат.

Статья имеет своей целью развенчать необходимость использования термина «замедление» при решении практических задач механики, и, если читателя не смущает очередная лекция по теормеху, добро пожаловать под кат.

1. Понятие производной от вектора по времени

Рассмотрим вектор , такой, что

то есть модуль и направление этого вектора зависят от времени. Вычислим изменение изменение этого вектора, произошедшее за промежуток времени

Теперь, используя тот факт, что для векторов определена операция умножения на число, умножим (1) на величину, обратную приращению времени . В силу того, что 0″/> мы получим вектор , направленный в ту же сторону что и вектор (1) (см. рисунок 1)

Рис. 1. Геометрический смысл производной вектора по времени

Теперь перейдем к пределу при

Соотношение (2) есть предел отношения приращения вектор-функции к приращению её аргумента и называется производной вектора по времени. Как видно из наших выкладок производная от вектора по времени также является вектором. Как направлен этот вектор?

Будем рассуждать, глядя на геометрическую интерпретацию на рисунке 1. Вектор занимает положение секущей по отношению к траектории, которую описывает конец вектора за промежуток времени . Эта траектория называется годографом вектор-функции . Секущая пересекает годограф в точках A и B. При стремлении к нулю точка A остается неподвижной, а точка B смещается в сторону точки A. В пределе секущая займет положение касательной к годографу в точке A.

То есть, можно ввести следующее определение

Производная от вектора по времени есть вектор , направленный по касательной к годографу вектора

Таким образом, производная от вектора показывает, каким образом меняется как модуль, так и направление вектора. Ни о каком «знаке» производной тут речи не идет в принципе. И не может идти — производная от вектора по времени это так же вектор, а для вектора нет понятия знака.

2. Производная от вектора, постоянного по модулю

Допусти теперь что наш вектор обладает неизменной длиной, то есть

а меняется лишь его направление в пространстве. Будет ли у этого вектора отличная от нуля производная? Конечно будет! Умножим вектор скалярно сам на себя

Продифференцируем (3) по времени

Производная от модуля вектора равна нулю, ведь модуль не меняется во времени. Тогда, используя правило дифференцирования произведения раскрываем левую часть (4)

используя свойство коммутативности скалярного произведения, получаем

То есть, скалярное произведение вектора на собственную производную равно нулю а значит

Таким образом, производная вектора с постоянной длиной не только не равна нулю, а она есть вектор, перпендикулярный исходному. Годографом такого вектора будет окружность с радиусом, равным длине вектора (рисунок 2).

Мы сталкиваемся с такой ситуацией, когда вычисляем ускорение точки, движущейся равномерно по окружности. У неё есть центростремительное ускорение, перпендикулярное вектору скорости.

Производная от вектора будет равна нулю лишь в том случае, если вектор не меняет ни модуль, ни направление.

Рис 2. Вектор с постоянной длиной, его годограф и производная

3. Скорость и ускорение

Вектором скорости точки называется первая производная от радиус-вектора точки по времени

Вектор скорости точки направлен по касательной к её траектории.

Все верно — траектория и есть годограф радиус-вектора, причем выбор начала отсчета O из которого мы выпускаем радиус-вектор роли не играет.

Рис. 3. Векторы скорости и ускорения материальной точки

Аналогичным образом вводится и понятие ускорения

Вектор ускорения точки есть первая производная от вектора скорости точки по времени

Вектор ускорения направлен по касательной к годографу вектора скорости.

Геометрическая иллюстрация этих определений показана на рисунке 3. При движении точки по окружности с постоянной по модулю скоростью ускорение направлено точно к центру этой окружности (рисунок 4)

в полном соответствии с определением производной от вектора постоянного по модулю. В этом случае вектор ускорения как раз показывает каким образом меняется направление вектора скорости.

Заключение или откуда всё-таки берется знак

Решая задачу по механике мы неизбежно переходим от векторных уравнений к уравнениям в проекциях на оси выбранной системы координат. И, если вектор ускорения направлен против вектора скорости, то знак его проекции отличается от знака проекции вектора скорости. Причем последняя может быть отрицательной, а проекция ускорения — положительной, все зависит от выбранной системы координат!. Именно в этой ситуации в инженерной практике употребляют термин «замедление».

Однако знак проекции и её именование к механике отношения не имеют, они относятся уже к формальной процедуре вычислений при решении задачи и механического смысла не несут. Так что понятие «замедление» есть результат вольной интерпретации промежуточных результатов вычислений.

Источник