Что показывает знак ковариации
Ковариация
которая может быть получена из первой формулы, используя свойства математического ожидания. Перечислим основные свойства ковариации.
1. Ковариация случайной величины с самой собой есть ее дисперсия.
2. Ковариация симметрична.
$$cov\left(X,\ Y\right)=cov\left(Y,\ X\right).$$
4. Постоянный множитель можно выносить за знак ковариации.
$$cov\left(cX,\ Y\right)=cov\left(X,\ cY\right)=c\cdot cov\left(X,\ Y\right).$$
5. Ковариация не изменится, если к одной из случайных величин (или двум сразу) прибавить постоянную величину:
$$cov\left(X+c,\ Y\right)=cov\left(X,\ Y+c\right)=cov\left(X+x,\ Y+c\right)=cov\left(X,\ Y\right).$$
9. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий плюс (минус) удвоенная ковариация этих случайных величин:
$$D\left(X\pm Y\right)=D\left(X\right)+D\left(Y\right)\pm 2cov\left(X,\ Y\right).$$
$$M\left(X\right)=\sum^n_
$$M\left(Y\right)=\sum^n_
$$M\left(XY\right)=\sum_
Корреляция
Перечислим основные свойства коэффициента корреляции.
При копировании материала с сайта, обратная ссылка обязательна!
Повторение статистики для начала путешествия по науке о данных
Введение
Предположим, у нас есть диаграмма рассеяния, на которой каждая точка — это человек. На одной оси показан его профессиональный опыт в годах, на другой — доход.
В соответствии с диаграммой справа можно заключить, что между опытом и доходом нет никакой связи, то есть определенный опыт оплачивается по-разному.
Слева, наоборот, между признаками существует четкая линейная зависимость.
Ковариация и корреляция показывают, насколько тесно между собой связаны переменные набора данных.
N.B: в приведенном примере представлен двумерный вид данных (с двумя переменными). На практике статистики используют многомерные данные (со множеством переменных).
Ковариация
Ковариация — это мера зависимости между двумя или более случайных переменных.
С английского «covariance» = «co» (совместность/соединение) + «variance» (дисперсия). То есть ковариация похожа на дисперсию, но она применяется для сравнения двух переменных, где вместо суммы квадратов, мы получаем сумму векторного произведения.
Дисперсия показывает, насколько определенная переменная отличается от среднего значения, а ковариация — насколько две переменные отличаются друг от друга. Таким образом, можно утверждать следующее:
Ковариация измеряет дисперсию между двумя переменными.
Ковариация может быть отрицательной, положительной и нулевой: положительное значение показывает, что две переменные изменяются в одном направлении (если одна переменная увеличивается, то и вторая тоже увеличивается); отрицательное значение показывает, что две переменные изменяются в разных направлениях (одна увеличивается, вторая уменьшается); нулевая ковариация означает, что они изменяются независимо друг от друга.
Формула
Формулу сложно объяснить, но важно понять, что она означает:
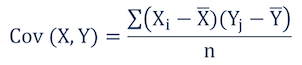
Предположим, что набор данных со случайными переменными представлен в виде вектора. Тогда в прошлом примере у нас есть два вектора для опыта и дохода. Ниже приведен порядок действий:
На втором этапе измеряется угол между двумя векторами. Если угол острый, то переменные тесно связаны между собой.
Ограниченность
Следует отметить, что несмотря на то, что ковариация измеряет зависимость между направлениями двух переменных, она не показывает тесноту этой зависимости.
На практике самая большая проблема с этой мерой заключается в том, что она зависит от используемой единицы измерения. Например, необходимо перевести годы опыта в месяцы. Тогда ковариация будет в 12 раз больше.
В этом случае на помощь приходит корреляция!
Корреляция
Корреляция — одна из наиболее распространенных мер в статистике, описывающая тесноту взаимосвязи между двумя случайными переменными. Она считается нормализованной версией ковариации. Давайте рассмотрим, почему…
Формула
Корреляция (обозначаемая греческой буквой «ро» — ρ) рассчитывается по следующей формуле:
Обратите внимание, что функциональная связь редко встречается на практике, так как две случайные переменные обычно не сопоставляются друг с другом на основе постоянного значения.
Корреляция, равная 0, означает, что между двумя переменными нет линейной зависимости. Тогда может быть отношение x = y².
Ключевые свойства
Корреляция — безразмерная величина, указывающая не только на направление взаимосвязи, но и на ее тесноту (в зависимости от того, насколько большим является абсолютное значение). Единицы измерения исключены из-за того, что ковариацию разделили на среднеквадратическое отклонение.
Напоследок необходимо запомнить, что корреляция не является причинно-следственной связью. Высокая корреляция между двумя случайными переменными просто означает, что они связаны друг с другом, но их взаимоотношение не обязательно должен иметь причинно-следственный характер. Доказать причинно-следственную связь можно только с помощью контролируемых экспериментов, при которых внешние переменные исключаются и эффекты двух данных переменных изолируются.
Ковариация и коэффициент корреляции
Ранее была рассмотрена диаграмма разброса, иллюстрирующая распределение двумерных числовых данные (см. последний раздел Изображение двумерных числовых данных заметки Представление числовых данных в виде таблиц и диаграмм). В настоящей заметке мы изучим два количественных показателя, характеризующих силу зависимости между двумя переменными — ковариацию и коэффициент корреляции. [1] Ковариация оценивает силу линейной зависимости между двумя числовыми переменными X и Y. Выборочная ковариация:
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Рассмотрим пятилетнюю среднегодовую доходность и долю затрат в фондах с очень низким уровнем риска (рис. 1). Для расчета ковариации двух выборок в Excel до 2007 года используется функция =КОВАР(), начиная с версии 2010 – функция КОВАРИВЦИЯ.В().
Рис. 1. Пятилетняя среднегодовая доходность и доля затрат взаимных фондов с очень низким уровнем риска
Любопытно, что ковариация случайной величины с собой равна дисперсии:
Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать. Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий. Масштаб можно отнормировать, поделив значение ковариации на произведение среднеквадратических отклонений (квадратных корней из дисперсий). При этом получается так называемый коэффициент корреляции Пирсона.
Относительная сила зависимости, или связи, между двумя переменными, образующими двумерную выборку, измеряется коэффициентом корреляции, изменяющимся от –1 для идеальной обратной зависимости до +1 для идеальной прямой зависимости. Коэффициент корреляции обозначается греческой буквой ρ. Линейность корреляции означает, что все точки, изображенные на диаграмме разброса, лежат на прямой (рис 2). На панели А изображена обратная линейная зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен –1, т.е., когда переменная X возрастает, переменная Y убывает. На панели Б показана ситуация, в которой между переменными X и Y нет корреляции. В этом случае коэффициент корреляции ρ равен 0, и, когда переменная X возрастает, переменная Y не проявляет никакой определенной тенденции: она ни убывает, ни возрастает. На панели В изображена линейная прямая зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен +1, и, когда переменная X возрастает, переменная Y также возрастает.
Рис. 2. Три вида зависимости между двумя переменными
Рис. 3. Шесть диаграмм разброса и соответствующие коэффициенты корреляции, полученные с помощью программы Excel
На панели А показана ситуация, в которой выборочный коэффициент корреляции r равен –0,9. Прослеживается четко выраженная тенденция: небольшим значениям переменной X соответствуют очень большие значения переменной Y, и, наоборот, большим значениям переменной X соответствуют малые значения переменной Y. Однако данные не лежат на одной прямой, поэтому зависимость между ними нельзя назвать линейной. На панели Б приведены данные, выборочный коэффициент корреляции между которыми равен –0,6. Небольшим значениям переменной X соответствуют большие значения переменной Y. Обратите внимание на то, что зависимость между переменными X и Y нельзя назвать линейной, как на панели А, и корреляция между ними уже не так велика. Коэффициент корреляции между переменными X и Y, изображенными на панели В, равен –0,3. Прослеживается слабая тенденция, согласно которой большим значениям переменной X, в основном, соответствуют малые значения переменной Y. Панели Г–Е иллюстрируют положительную корреляцию между данными — малым значениям переменной X соответствуют большие значения переменной Y.
Обсуждая рис. 3, мы употребляли термин тенденция, поскольку между переменными X и Y нет причинно-следственных связей. Наличие корреляции не означает наличия причинно-следственных связей между переменными X и Y, т.е. изменение значения одной из переменных не обязательно приводит к изменению значения другой. Сильная корреляция может быть случайной и объясняться третьей переменной, оставшейся за рамками анализа. В таких ситуациях необходимо проводить дополнительное исследование. Таким образом, можно утверждать, что причинно-следственные связи порождают корреляцию, но корреляция не означает наличия причинно-следственных связей.
Выборочный коэффициент корреляции:
В Excel для вычисления коэффициента корреляции используется функция =КОРРЕЛ() (рис. 4).
Рис. 4. Функция КОРРЕЛ в Excel
Итак, коэффициент корреляции свидетельствует о линейной зависимости, или связи, между двумя переменными. Чем ближе коэффициент корреляции к –1 или +1, тем сильнее линейная зависимость между двумя переменными. Знак коэффициента корреляции определяет характер зависимости: прямая (+) и обратная (–). Сильная корреляция не является причинно-следственной зависимостью. Она лишь свидетельствует о наличии тенденции, характерной для данной выборки.
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 221–227
Корреляция, ковариация и девиация (часть 3)
В первой части показано, как на основе матрицы расстояний между элементами получить матрицу Грина. Ее спектр образует собственную систему координат множества, центром которой является центроид набора. Во второй рассмотрены спектры простых геометрических наборов.
В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.
7. Векторизация и нормирование одномерных координат
Пусть значения некой характеристики элементов заданы рядом чисел . Для того, чтобы данный набор можно было сравнивать с другими характеристиками, необходимо его векторизовать и обезразмерить (нормировать).
Для векторизации находим центр (среднее) значений
и строим новый набор как разность между исходными числами и их центроидом (средним):
Получили вектор. Основной признак векторов состоит в том, что сумма их координат равна нулю. Далее нормируем вектор, — приведем сумму квадратов его координат к 1. Для выполнения данной операции нам нужно вычислить эту сумму (точнее среднее):
Теперь можно построить ССК исходного набора как совокупность собственного числа S и нормированных координат вектора:
Квадраты расстояний между точками исходного набора определяются как разности квадратов компонент собственного вектора, умноженные на собственное число. Обратим внимание на то, что собственное число S оказалось равно дисперсии исходного набора (7.3).
Итак, для любого набора чисел можно определить собственную систему координат, то есть выделить значение собственного числа (она же дисперсия) и рассчитать координаты собственного вектора путем векторизации и нормирования исходного набора чисел. Круто.
Упражнение для тех, кто любит «щупать руками». Построить ССК для набора <1, 2, 3, 4>.
8. Векторизация и ортонормирование многомерных координат
Что, если вместо набора чисел нам задан набор векторов — пар, троек и прочих размерностей чисел. То есть точка (узел) задается не одной координатой, а несколькими. Как в этом случае построить ССК? Стандартный путь следующий.
Введем обозначение характеристик (компонент) набора. Нам заданы точки (элементы) и каждой точке соответствует числовое значение характеристики
. Обращаем внимание, что второй индекс
— это номер характеристики (столбцы матрицы), а первый индекс
— номер точки (элемента) набора (строки матрицы).
Далее векторизуем характеристики. То есть для каждой находим центроид (среднее значение) и вычитаем его из значения характеристики:
Получили матрицу координат векторов (МКВ) .
Следующим шагом как будто бы надо вычислить дисперсию для каждой характеристики и их нормировать. Но хотя таким образом мы действительно получим нормированные векторы, нам-то нужно, чтобы эти векторы были независимыми, то есть ортонормированными. Операция нормирования не поворачивает вектора (а лишь меняет их длину), а нам нужно развернуть векторы перпендикулярно друг другу. Как это сделать?
Правильный (но пока бесполезный) ответ — рассчитать собственные вектора и числа (спектр). Бесполезный потому, что мы не построили матрицу, для которой можно считать спектр. Наша матрица координат векторов (МКВ) не является квадратной — для нее собственные числа не рассчитаешь. Соответственно, надо на основе МКВ построить некую квадратную матрицу. Это можно сделать умножением МКВ на саму себя (возвести в квадрат).
Но тут — внимание! Неквадратную матрицу можно возвести в квадрат двумя способами — умножением исходной на транспонированную. И наоборот — умножением транспонированной на исходную. Размерность и смысл двух полученных матриц — разный.
Умножая МКВ на транспонированную, мы получаем матрицу корреляции:
Из данного определения (есть и другие) следует, что элементы матрицы корреляции являются скалярными произведениями векторов (грамиан на векторах). Значения главной диагонали отражают квадрат длины данных векторов. Значения матрицы не нормированы (обычно их нормируют, но для наших целей этого не нужно). Размерность матрицы корреляции совпадает с количеством исходных точек (векторов).
Теперь переставим перемножаемые в (8.1) матрицы местами и получим матрицу ковариации (опять же опускаем множитель 1/(1-n), которым обычно нормируют значения ковариации):
Здесь результат выражен в характеристиках. Соответственно, размерность матрицы ковариации равна количеству исходных характеристик (компонент). Для двух характеристик матрица ковариации имеет размерность 2×2, для трех — 3×3 и т.д.
Почему важна размерность матриц корреляции и ковариации? Фишка в том, что поскольку матрицы корреляции и ковариации происходят из произведения одного и того же набора векторов, то они имеют один и тот же набор собственных чисел, один и тот же ранг (количество независимых размерностей) матрицы. Как правило, количество векторов (точек) намного превышает количество компонент. Поэтому о ранге матриц судят по размерности матрицы ковариации.
Диагональные элементы ковариации отражают дисперсию компонент. Как мы видели выше, дисперсия и собственные числа тесно связаны. Поэтому можно сказать, что в первом приближении собственные числа матрицы ковариации (а значит, и корреляции) равны диагональным элементам (а если межкомпонентная дисперсия отсутствует, то равны в любом приближении).
Если стоит задача найти просто спектр матриц (собственные числа), то удобнее ее решать для матрицы ковариации, поскольку, как правило, их размерность небольшая. Но если нам необходимо найти еще и собственные вектора (определить собственную систему координат) для исходного набора, то необходимо работать с матрицей корреляции, поскольку именно она отражает скалярное произведение векторов.
Отметим, что метод главных компонент как раз и состоит в расчете спектра матрицы ковариации/корреляции для заданного набора векторных данных. Найденные компоненты спектра располагаются вдоль главных осей эллипсоида данных. Из нашего рассмотрения это вытекает потому, что главные оси — это и есть те оси, дисперсия (разброс) данных по которым максимален, а значит, и максимально значение спектра.
Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.
9. Матрица Грина — это матрица корреляции векторов
Рассмотрим теперь ситуацию, когда нам известен не набор чисел, характеризующих точки (элементы), а набор расстояний между точками (причем между всеми). Достаточно ли данной информации для определения ССК (собственной системы координат) набора?
Ответ дан в первой части — да, вполне. Здесь же мы покажем, что построенная по формуле (1.3′) матрица Грина и определенная выше матрица корреляции векторов (8.1) — это одна и та же матрица.
Как такое получилось? Сами в шоке. Чтобы в этом убедиться, надо подставить выражение для элемента матрицы квадратов расстояний
в формулу преобразования девиации:
Отметим, что среднее значение матрицы квадратов расстояний отражает дисперсию исходного набора (при условии, что расстояния в наборе — это сумма квадратов компонент):
Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):
Итак, матрица Грина и матрица корреляции векторов — суть одно и то же. Ранг матрицы корреляции совпадает с рангом матрицы ковариации (количеством характеристик — размерностью пространства). Это обстоятельство позволяет строить спектр и собственную систему координат для исходных точек на основе матрицы расстояний.
Для произвольной матрицы расстояний потенциальный ранг (количество измерений) на единицу меньше количества исходных векторов. Расчет спектра (собственной системы координат) позволяет определить основные (главные) компоненты, влияющие на расстояния между точками (векторами).
Таким образом можно строить собственные координаты элементов либо на основании их характеристик, либо на основании расстояний между ними. Например, можно определить собственные координаты городов по матрице расстояний между ними.
Может ли ковариация быть больше 1?
ковариационная похожа на корреляцию между двумя переменными, однако они различаются следующим образом: Коэффициенты корреляции стандартизированы. Таким образом, идеальная линейная зависимость дает коэффициент 1. … Следовательно ковариация может варьируются от отрицательной бесконечности до положительной бесконечности.
Впоследствии, что такое ковариация P в Excel?
Функция P в Microsoft Excel. Возвращает ковариацию населения, среднее значение продуктов отклонений для каждой пары точек данных в двух наборах данных. Используйте ковариацию, чтобы определить взаимосвязь между двумя наборами данных. Например, вы можете проверить, сопровождает ли более высокий доход более высокий уровень образования.
Кроме того, всегда ли ковариация находится между 0 и 1?
«Мы сказали, что если случайные величины независимы, то их ковариация равна 0; Однако обратное не обязательно верно. То есть, если ковариация двух случайных величин равна 0, это не обязательно означает, что они независимы.
Во-вторых, почему ковариация отрицательная? При изменении обе переменные движутся вместе в одном направлении. Уменьшение одной переменной приводит к противоположному изменению другой переменной называются отрицательной ковариацией. Эти переменные обратно связаны и всегда движутся в разных направлениях.
Что означает корреляция 1?
Корреляция –1 указывает на то, что идеальная отрицательная корреляция, что означает, что по мере того, как одна переменная растет, другая уменьшается. Корреляция +1 указывает на идеальную положительную корреляцию, что означает, что обе переменные вместе движутся в одном направлении. Корреляции играют важную роль в исследованиях психологии.
Что такое корреляция и ковариация в статистике?
Проще говоря, оба термина измеряют взаимосвязь и зависимость между двумя переменными. «Ковариация »указывает направление линейной зависимости между переменными.. «Корреляция», с другой стороны, измеряет как силу, так и направление линейной связи между двумя переменными.
Что такое ковариация в статистике?
Ковариация статистический инструмент, который используется для определения взаимосвязи между движением цен двух активов. Когда две акции имеют тенденцию двигаться вместе, считается, что они имеют положительную ковариацию; когда они движутся в обратном направлении, ковариация отрицательная.
Можете ли вы сделать корреляцию в Excel?
Чтобы использовать надстройку Analysis Toolpak в Excel для быстрого создания коэффициентов корреляции между несколькими переменными, выполните следующие действия.
Как показать, что ковариация равна нулю?
Что такое положительная ковариация?
Ковариация измеряет направленную связь между доходностью двух активов. Положительная ковариация означает что доходность активов движется вместе в то время как отрицательная ковариация означает, что они движутся обратно.
В чем разница между ковариацией и корреляцией?
Различия между ковариацией и корреляцией.
Насколько хороша отрицательная ковариация?
Положительная ковариация указывает на то, что два актива движутся в тандеме. А отрицательная ковариация указывает на то, что два актива движутся в противоположных направлениях. При построении портфеля важно попытаться снизить общий риск и волатильность, одновременно стремясь к положительной норме доходности.
Как узнать, отрицательна ли ковариация?
На что указывает отрицательная ковариация?
Отрицательная ковариация указывает на то, что движение одной переменной противоположно движению другой переменной.
Может ли корреляция быть больше 1?
Каков пример нулевой корреляции?
Нулевая корреляция существует, когда нет связи между двумя переменными. Например есть нет связи между количеством выпитого чая и уровнем интеллекта.
В чем разница между корреляцией и ковариацией?
Различия между ковариацией и корреляцией.
Как вы рассчитываете ковариацию и корреляцию?
Приведенное выше уравнение показывает, что корреляция между двумя переменными ковариация между обеими переменными, деленная на произведение стандартного отклонения переменных.
В чем разница между корреляцией и регрессией?
Как найти ковариацию на калькуляторе?
Как рассчитать ковариацию по TI-84
Как рассчитать стандартное отклонение?
Чтобы вычислить стандартное отклонение этих чисел:
Что такое корреляционная функция в Excel?
CORREL формула в Excel используется для определения коэффициента корреляции между двумя переменными. Он возвращает коэффициент корреляции array1 и array2. Вы можете использовать коэффициент корреляции, чтобы определить взаимосвязь между двумя свойствами.