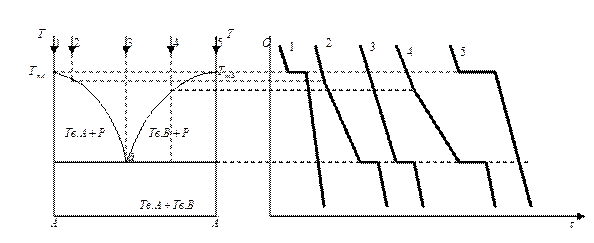Что показывают кривые охлаждения и как они строятся
Кристаллизация металлов. Построение кривых охлаждения
. Процесс образования кристаллов при затвердевании металла называется кристаллизацией. При кристаллизации металла выделяется теплота, при переходе же металла из твердого состояния в жидкое происходит поглощение теплоты.
Сначала температура понижается равномерно. В начальный период образования кристаллов вследствие выделения скрытой теплоты при формировании кристаллической решетки падение температуры прекращается, и она остается неизменной до полного затвердения металла. После того, как весь металл затвердеет, температура снова начинает понижаться. Температура, соответствующая горизонтальной площадке, называется критической.
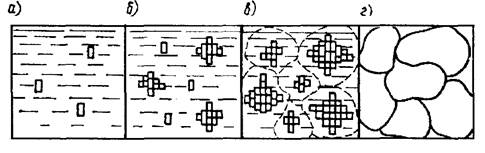
Последовательные этапы процесса кристаллизации показаны на рисунке 1.5. Первый этап — появление зародышей кристаллов. По мере остывания металла к зародышам присоединяются все новые и новые атомы жидкого металла, которые группируются в определенном порядке один возле другого, образуя элементарные ячейки кристаллической решетки (элементарная ячейка изображена в виде прямоугольников). Этот процесс продолжается до тех пор, пока не закончится кристаллизация.
Кристаллы затвердевшего металла имеют неправильную и разнообразную внешнюю форму, что объясняется условиями кристаллизации. В процессе кристаллизации увеличивается количество кристаллов (в 1 мм 3 может образоваться свыше 1000 кристаллов). При соприкосновении грани смежных кристаллов мешают друг другу принять геометрически правильную внешнюю форму.
Кристаллы, имеющие неправильную внешнюю форму, называются кристаллитами, или зернами. Размер зерен зависит от условий кристаллизации, и прежде всего, от скорости охлаждения металла.
а — появление зародышей кристаллов; б — рост кристаллов и образование новых центров; в — рост кристаллов; г — границы кристаллов (зерен) затвердевшего металла
Чем больше скорость охлаждения металла, тем быстрее он затвердевает, тем больше возникает центров кристаллизации и, следовательно, тем меньшего размера получаются зерна. В тонких быстро охлаждающихся сечениях литых деталей металл имеет более мелкое зерно, чем в толстых массивных охлаждение медленнее. Однако скорость охлаждения не всегда можно регулировать. Мелкое зерно при затвердевании металла образуется в случае создания искусственных центров кристаллизации. Для этого в расплавленный металл вводят специальные вещества, называемые модификаторами. Процесс искусственного регулирования размеров зерен называется модифицированем.
Форма растущих кристаллов зависит не только от условий их столкновения между собой, но также от состава сплава, наличия примесей и условий охлаждения.
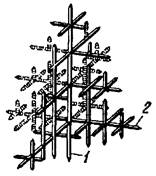
Механизм образования кристаллов в большинстве случаев носит так называемый дендритный характер. При дендритной кристаллизации рост зародышей кристаллов происходит с неравномерной скоростью. После образования зародышей их развитие идет в тех направлениях решетки, которые имеют наибольшую плотность расположения атомов (минимальное межатомное расстояние). В этих направлениях возникают длинные ветви будущего кристалла — оси первого порядка. От осей первого порядка под определенными углами растут новые оси — оси второго порядка 1, от осей второго порядка — оси третьего порядка 2. По мере кристаллизации образуются оси более высокого порядка (четвертого, пятого, шестого и т. д.), которые постепенно заполняют нее промежутки, ранее занятые жидким металлом.
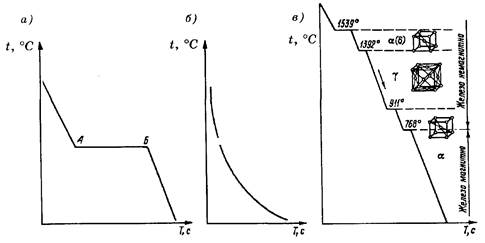
Для определения критических температур кристаллизации и других параметров металлов строят кривые охлаждения.
Для медленно охлаждающегося чистого металла кривая охлаждения будет иметь вид. Кривая охлаждения свидетельствует о том, что жидкий металл охлаждается равномерно до точки А. В точке А понижение температуры прекращается. Между точками А и Б находится участок критической температуры, при которой начинается и заканчивается кристаллизация металла. Далее температура вновь понижается равномерно. Кривая охлаждения сплава (она станет понятна после изучения аллотропических превращений).
Охлаждение аморфного тела протекает плавно, так как оно постепенно отвердевает вследствие уменьшения подвижности частиц. Кажущееся твердым аморфное тело по структуре представляет собой переохлажденную жидкость.
Дата добавления: 2015-11-10 ; просмотров: 5759 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Построение кривых охлаждения сплавов
Теория
Химические элементы, оставляющие сплав, называются его компонентами. В общем виде будем их обозначать А и В.
Вид диаграммы состояния полностью определяется характером физико-химического взаимодействия его компонентов между собой. Будем в дальнейшем рассматривать лишь такие сплавы, которые могут быть полностью расплавлены. Тогда можно считать, что при достаточно высоких температурах любые сплавы представляют собой однородный жидкий раствор компонентов, который на всех диаграммах будем обозначать через L (жидкость).
В твердом состоянии компоненты внутри сплава могут в общем случае взаимодействовать следующим образом:
1)химически реагировать друг с другом с образованием нового вещества –химического соединенияAmBn:
2)растворяться в кристаллической решетке друг друга полностью либо частично, при этом образуются твёрдые растворы (например, твердый раствор А в В);
В соответствии с этим определением в общем случае фазами в сплавах могут быть:
При проведении анализа диаграммы состояний необходимо сначала по характерным линиям диаграммы определить вид взаимодействия компонентов в сплавах данной системы, затем выявить однофазные области на диаграмме. После этого с помощью правила отрезков (см. ниже) определить фазовый состав сплавов в остальных (двухфазных) областях диаграммы состояний и, на конец, построением кривых охлаждения для конкретных сплавов системы определить возможные структуры сплавов в охлажденном состоянии.
Правило отрезков
Правило отрезков служит для определения:
1)фазового состава сплава в заданной точке диаграммы состояния;
2)химического состава фаз, имеющихся в сплаве;
3)весовой доли каждой фазы
С этой целью, вначале из заданной точки на диаграмме состояния необходимо провести отрезок горизонтали влево и вправо до пересечения с границами ближайших однофазных областей, а затем на этом отрезке необходимо определить все точки его контакта (т.е. пересечения и касания) с однофазными областями (рис. 1).
Рис. 1. Применение правила отрезков при анализе диаграмм состояний.
1.Задана т. а, проведен отрезок bac, определены точки b и с.
2.Задана т. d, проведен отрезок fde, отмечены точки f и е.
3.Задана т. q, проведен отрезок hiqk, отмечены точки h, i, k.
В дальнейшем, по определенным (отмеченным) точкам пересечения и касания с однофазными областями можно для заданной начальной точки определить фазовый состав сплава, химический состав фаз в сплаве и весовую долю каждой фазы.
1)Фазовый состав сплава определяется по принадлежности каждой отмеченной точки к однофазной области
В примере 2: в заданной т. d фазовый состав сплава: А+В.
В примере 3: заданной т. q фазовый состав сплава: A+B+L.
2)Химический состав фаз определяется по проекциям отмеченных точек на ось концентраций.
3)Весовую долю фазы- определяют по правилу рычага, как отношение противолежащей фазе части отрезка ко всей его длине
В примере 1: Q А= 

В примере 2: QA = 

Замечание: при наличии в сплаве более двух фаз применять правило рычага не следует.
Помимо определения фазового состава сплава, с помощью правила отрезков можно определить и структурный состав. В этом случае отрезок горизонтали необходимо проводить до пересечения с границами областей структурных составляющих. Например, если задана т. l(рис.2), то проводим отрезок nlm, и отмеченные точки nиmуказывают, что в заданной точке l сплав имеет структуру: эвт (А+В)+ кристаллы В; в эвтектике содержится n ‘ % B (проекция т.n); в кристаллах B-100%В (проекция т.m);
100% В (проекция т. т); весовая доля эвтектики в структурном сплаве
Qэвт=
Доля кристаллов В в структуре сплава
QB= 
Правило фаз (правило Гиббса)
В данной работе это правило используется, в основном, для контроля хода кривых охлаждения сплавов. Правило имеет вид:
Если С>0 (т.е. С = 1 или 2), то температура сплава будет монотонно понижаться при отводе тепла от сплава. Если в некоторой точке происходит изменение от С = 1 к С = 2 или наоборот, то изменяется скорость снижения температуры сплава, т.е. в этих точках на кривой охлаждения будут изломы.
Если С = 0, то несмотря на отвод тепла от сплава, его температура будет оставаться постоянной до тех пор, пока не завершится какой-то процесс внутри сплава, благодаря чему в нем уменьшится число фаз и окажется C>0. На кривой охлаждения сплава этому процессу будет соответствовать горизонтальный участок.
Построение кривых охлаждения сплавов
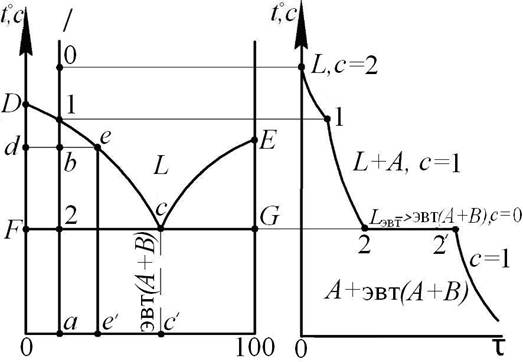
Рассмотрим в качестве примера построение кривой охлаждения для сплава эвтектического типа (рис.2).
Рис.2.Пример построения кривой охлаждения
Начальный участок кривой охлаждения (выше т. 1). Для любой точки этого участка фазовый состав сплава: L, так как этот участок находится в однофазной области диаграммы. Следовательно, число фаз в сплаве Ф = 1, и по правилу фаз, число степеней свобода сплава С = 2. Следовательно, при отводе тепла температура сплава монотонно понижается и этот участок кривой охлаждения изобразится плавной падающей линией: возле этого участка на кривой охлаждения указываем фазовый состав и число степеней свободы сплава: L, С = 2.
Участок 1-2. Для любой точки b на этом участке по правилу отрезков устанавливаем фазовый состав сплава: L (т. е) + А (т. d), следовательно, Ф = 2 и по правилу фаз С = 1. Значит, этот участок кривой охлаждения, как и предыдущий, будет изображаться плавной линией, возле которого следует указать: L + А, С = 1. В точке 1 кривой охлаждения будет излом, т.к. здесь изменяется число степеней свободы сплава от С = 2 к С = 1.
Перемещая т. b от т.1 к т. 2 и определяя весовую долю твердых кристаллов А
(QA = 
то есть на участке 2—2 / в сплаве идет эвтектическое превращение.
Конечный участок кривой охлаждения (после т. 2 / ). После окончания эвтектического превращения в сплаве останутся две фазы: А и В, что легко проверяется правилом отрезков для любой точки диаграммы на участке 2-а. Таким образом, Ф = 2 и С = 1, так что сплав монотонно снижает свою температуру до комнатной.
На этом участке необходимо указать конечную структуру сплава. В данном простом случае это можно сделать по правилу отрезков (для структурных составляющих) на участке 2-а диаграммы.
Построение кривых охлаждения
При построении кривых охлаждения необходимо пользоваться правилом фаз: с=k – f + 1,
где с – вариантность системы (число степеней свободы), k – число компонентов, f – число фаз.
Количество компонент в данной системе всегда равно 2 – это железо и углерод.
Количество фаз находят, используя диаграмму.
Не следует путать фазы со структурными составляющими, так как последние могут быть однофазными и многофазными, а одна и та же фаза может входить в разные составляющие. Например, в доэвтектических чугунах при комнатной температуре цементит вторичный, цементит перлита и цементит ледебурита является одной и той же фазой. Структура этого чугуна – перлит + ледебурит + цементит, а фазовый состав – феррит + цементит. Рассуждения: перлит это двухфазная структурная составляющая, состоящая из феррита и цементита; ледебурит при комнатной температуре состоит из перлита и цементита, в свою очередь, перлит сам по себе тоже неоднороден и является смесью феррита и цементита; а структурная составляющая цементит – однофазна. Схематично эти рассуждения можно представить следующим образом:
Зная количество фаз и количество компонент, можно определить число степеней свободы. На линиях эвтектического, эвтектоидного и перитектического превращений система Fе – Fе3С находится в трехфазном состоянии, которое согласно правилу фаз является для двухкомпонентных систем нонвариантной: C=2-3+1=0. Все превращения при С = 0 происходят при постоянных температурах, и на кривой охлаждения они характеризуются горизонтальным участком.
В двухфазных областях диаграммы системы являются моновариантным:
С = 2-2+1=1, в связи с чем, превращения в сплавах в этих областях происходят в интервале температур. Выделение скрытой теплоты кристаллизации замедляет темп снижения температуры, поэтому участки кривых охлаждения в таких случаях будут пологими (с меньшим наклоном). Начало и конец превращений, когда изменяется вариантность системы, фиксируют на кривых охлаждения перегибами.
В однофазных областях системы биварианты: C=2-1+1=2. При этом с изменением температуры никаких превращений не происходит, и на кривых охлаждения будут крутые участки (с большим наклоном).
На рис. 5 приведен пример построения кривой охлаждения заэвтектоидной стали содержащей 1,5%С.
В точке 1 начинается процесс первичной кристаллизации, продолжающийся до точки 2, из жидкого раствора выпадают кристаллы аустенита. По мере охлаждения сплава от точки 1 до точки 2 концентрация компонентов в аустените изменяется согласно линии JЕ от точки J к точке 2, а в жидкости – согласно линии BC от точки 1 к точке 2¢ (рис. 3). Составы и количества фаз определяют по правилу отрезков. Например, в точке m состав жидкой фазы найдем проекцией точки n на ось концентраций, а состав твердой фазы – проекцией точки k.
Рис. 5. Диаграмма состояния Fe – C и кривая охлаждения для стали,
содержащей 1,5%С.
Количество фаз определяют из соотношения отрезков:
Ниже температуры 727°С в рассматриваемом сплаве практически не происходит превращений. По теоретическим данным, из феррита здесь выделяется третичный цементит, вследствие чего система будет моновариантной (С=2-2+1=1; фазы – феррит и цементит). Но феррит здесь содержится только в составе перлита, третичный цементит выделяется в незначительном количестве и металлографически не обнаруживается, так как сливается с цементитом перлита. Таким образом, в структуре стали данного состава при комнатной температуре наблюдаются зерна перлита, окаймленные тонкой сеткой вторичного цементита.
Превращения в сплавах в процессе нагрева происходят в обратной последовательности при некотором их перегреве выше температур равновесного состояния.
Вариантность (C) (число степеней свободы) – это число внутренних и внешних факторов (температура, давление, концентрация), которые можно изменять без изменения количества фаз в системе.
Если вариантность C = 1 (моновариантная система), то возможно изменение одного из факторов в некоторых пределах, без изменения числа фаз.
Если вариантность C = 0 (нонвариантная cистема), то внешние факторы изменять нельзя без изменения числа фаз в оистеме
Существует математическая связь между числом компонентов (К), числом фаз (Ф) и вариантностью системы ( С ). Это правило фаз или закон Гиббса
Если принять, что все превращения происходят при постоянном давлении, то число переменных уменьшится
где: С – число степеней свободы, К – число компонентов, Ф – число фаз, 1 – учитывает возможность изменения температуры.
Особенности строения, кристаллизации и свойств сплавов: механических смесей, твердых растворов, химических соединений
Определение количественного соотношения жидкой и твердой фазы при заданной температуре (в точке m):
Количественная масса фаз обратно пропорциональна отрезкам проведенной коноды. Рассмотрим проведенную через точку m коноду и ее отрезки.
Количество всего сплава (Qсп) определяется отрезком pq.
Отрезок, прилегающий к линии ликвидус pm, определяет количество твердой фазы.
Отрезок, прилегающий к линии солидус (или к оси компонента) mq, определяет количество жидкой фазы.
Диаграмма состояния сплавов с отсутствием растворимости компонентов в компонентов в твердом состоянии (механические смеси).
Диаграмма состояния и кривые охлаждения типичных сплавов системы представлены на рис. 6.
Рис. 6. Диаграмма состояния сплавов с отсутствием растворимости компонентов в твердом состоянии (а) и кривые охлаждения сплавов (б)
Проведем анализ диаграммы состояния.
1. Количество компонентов: К = 2 (компоненты А и В);
2. Число фаз: f = 3 (кристаллы компонента А, кристаллы компонента В, жидкая фаза).
3. Основные линии диаграммы:
— линия ликвидус acb, состоит из двух ветвей, сходящихся в одной точке;
— линия солидус ecf, параллельна оси концентраций стремится к осям компонентов, но не достигает их;
Диаграмму состояния строят в координатах температура-концентрация.
Рис. 7. Диаграмма состояния сплавов, образующих механические смеси.
Кривые охлаждения
Основы термического анализа
Основой термического анализа является построение кривых охлаждения. Кривые охлаждения – графические зависимости температуры охлаждающейся смеси от времени охлаждения. Для построения диаграммы плавкости требуется, как минимум, пять кривых охлаждения. Каждая кривая охлаждения будет соответствовать определенному составу охлаждаемой смеси и иметь свой вид.
1. Вначале охлаждается расплав гомогенной однокомпонентной однофазной системы. При достижении Тпл.А из расплава начинают выпадать кристаллы компонента А, система становиться однокомпонентной, двухфазной и инвариантной. На кривой охлаждения наблюдается температурная остановка. Так как тепло, выделяющееся при кристаллизации, компенсирует теплопотерю при охлаждении. Температурная остановка будет продолжаться настолько долго, пока в системе будет существовать две фазы. Остановка закончится тогда, когда из системы исчезнет последняя капля расплава, и она станет однокомпонентной, однофазной, моновариантной.
5. Вначале охлаждается расплав гомогенной однокомпонентной однофазной системы. При достижении Тпл.В из расплава начинают выпадать кристаллы компонента В, система становиться однокомпонентной, двухфазной и инвариантной. На кривой охлаждения наблюдается температурная остановка до тех пор, пока не останется ни капли расплава, и система станет однокомпонентной, однофазной, моновариантной. Температура вновь начинает уменьшаться.
Данные типы кривых охлаждения будут выполняться только в идеальных условиях, когда скорость охлаждения четко фиксируется путем постоянной разницы температур между охлаждающейся смесью и окружающей средой.
1. Диаграммы плавкости с образованием устойчивых химических соединений.
2. Диаграмма плавкости с образованием неустойчивого химического соединения.
3. Диаграммы плавкости двухкомпонентных систем с образованием твердых растворов.
Построение кривых охлаждения сплавов



Рассмотрим в качестве примера построение кривой охлаждения для сплава эвтектического типа (рис.3.6).
Рис. 3.6. Пример построения кривой охлаждения
Участок 1-2. Для любой точки b на этом участке по правилу отрезков устанавливаем фазовый состав сплава: L (т. e) + А (т. d), следовательно, f = 2 и по правилу фаз c = 1. Значит, этот участок кривой охлаждения, как и предыдущий, будет изображаться плавной линией, возле которого следует указать: L + А, c = 1. В точке 1 кривой охлаждения будет излом, так как здесь изменяется число степеней свободы сплава от c = 2 к c = 1.
Перемещая т. b от т.1 к т. 2 и, определяя весовую долю твердых кристаллов А – QA=(be/de) 100%, и химический состав жидкости в сплаве (е% В), можно легко установить, что на этом участке кривой охлаждения, начиная от т. 1, происходит выделение из жидкости твердых кристаллов А, а содержание компонента В в остающейся жидкости в сплаве постепенно увеличивается от а % В в т. 1 к значению с’ % В для т. 2, то есть из жидкости выделяются кристаллы компонента, избыточного по отношению к эвтектическому составу. В конце участка 1-2 сплав будет состоять из кристаллов А и оставшейся жидкости эвтектического состава.
Конечный участок кривой охлаждения (после т. 2). После окончания эвтектического превращения в сплаве останутся две фазы: А и В, что легко проверяется правилом отрезков для любой точки диаграммы на участке 2-а. Таким образом, f = 2 и c = 1, так что сплав монотонно снижает свою температуру до комнатной.