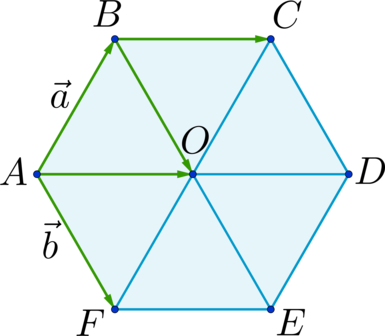
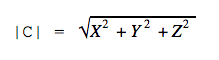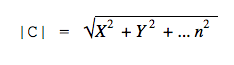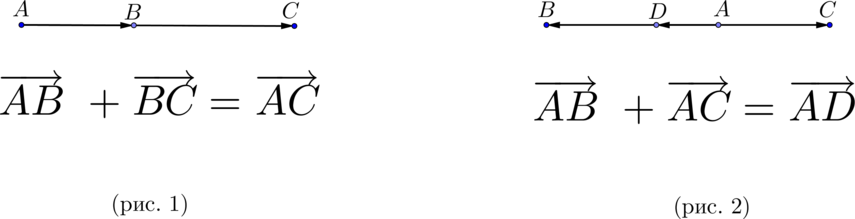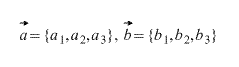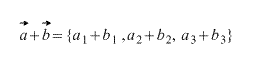Что получается при сложении векторов
Операции над векторами и их свойства: сложение и умножение
Прежде чем приступить к тематике статьи, напомним основные понятия.
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
Геометрически сложение векторов выглядит так:
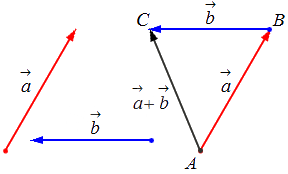
— для неколлинеарных векторов:
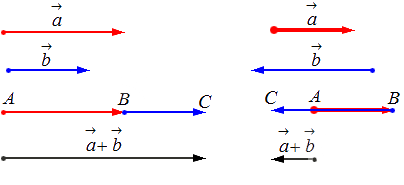
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
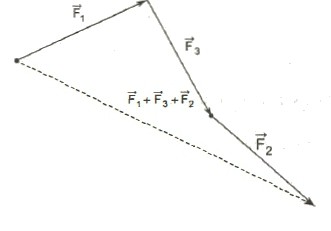
Сложение нескольких векторов
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
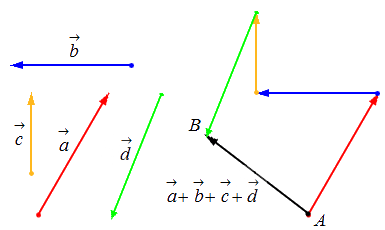
Геометрически оно выглядит следующим образом:
Умножение вектора на число
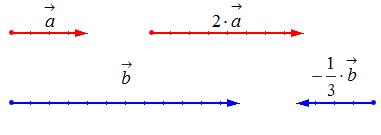
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Операции с векторами
Как сложить и перемножить векторы (и зачем).
Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Сложение
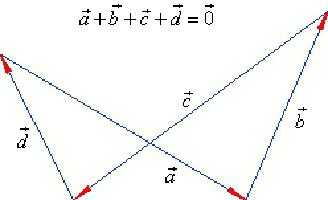
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
Векторы X, Y, Z, K в двухмерном пространстве
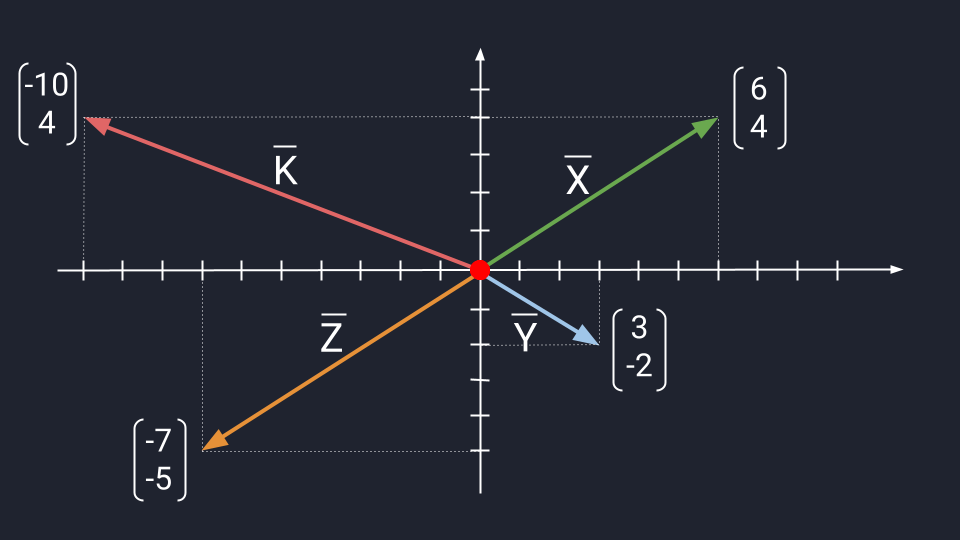
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
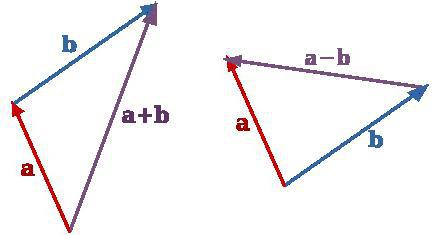
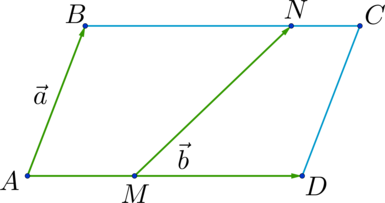
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)
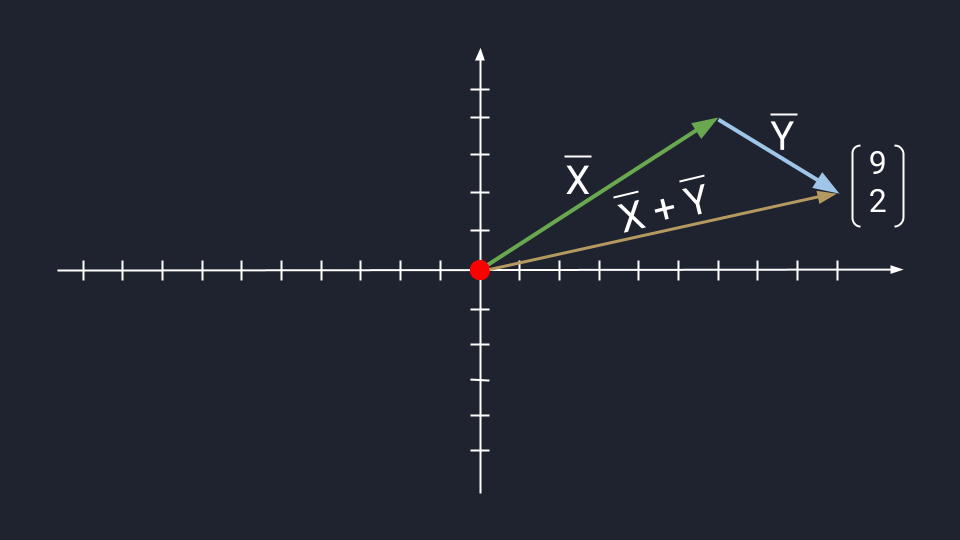
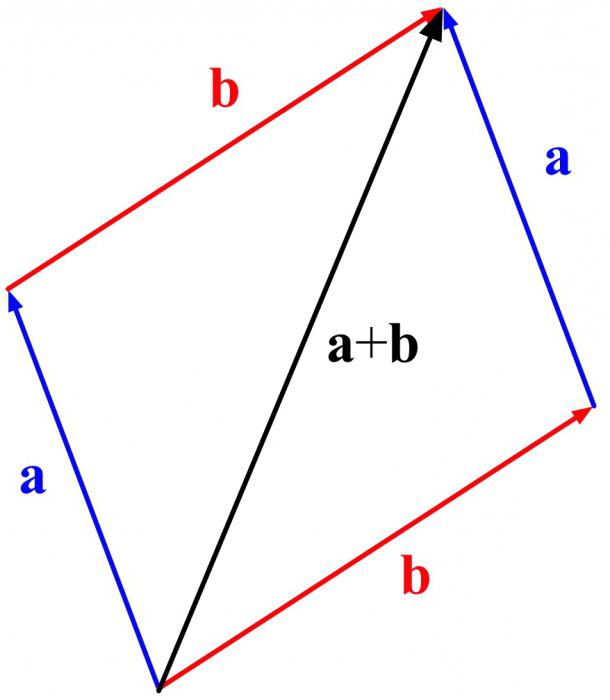
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
Вычитание
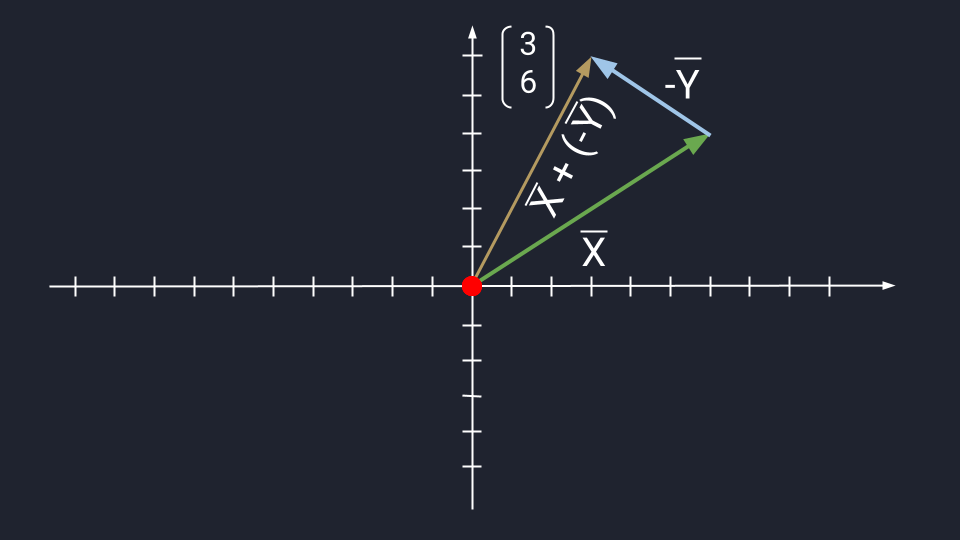
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
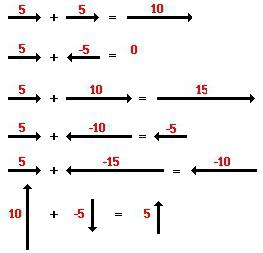
Дальше используются правила сложения. Пошагово это выглядит так:
Теперь посмотрим, как выглядит вычитание векторов на графике:
Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) 
Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)
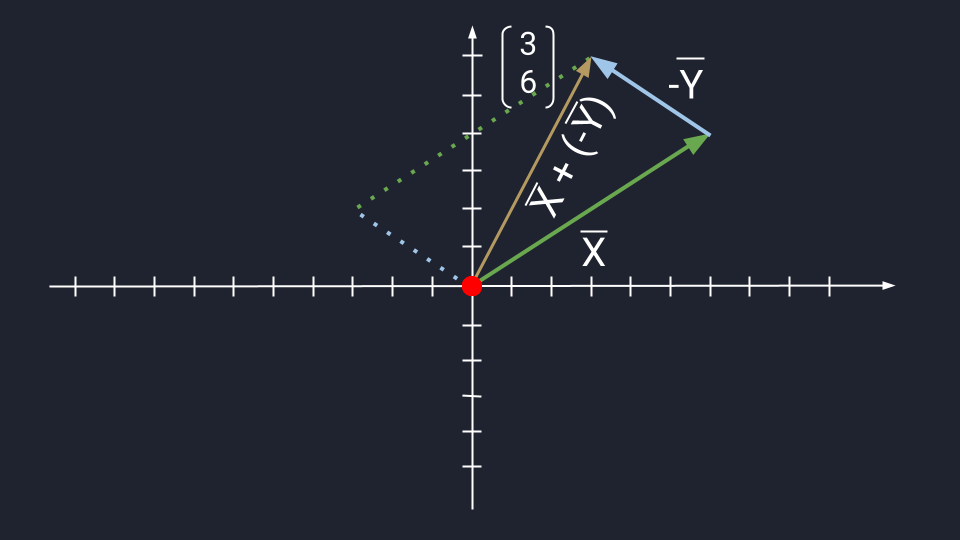
Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5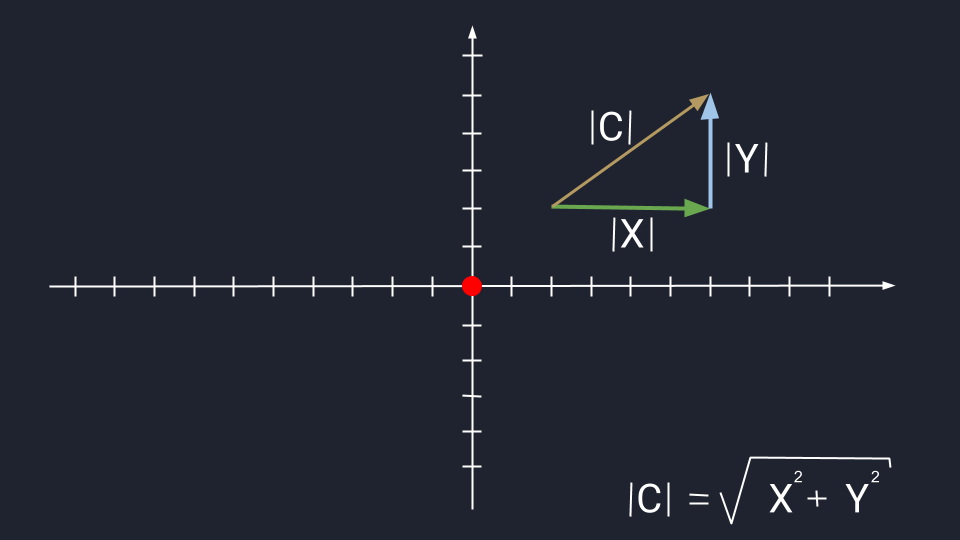 
Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
Умножение и деление вектора на число
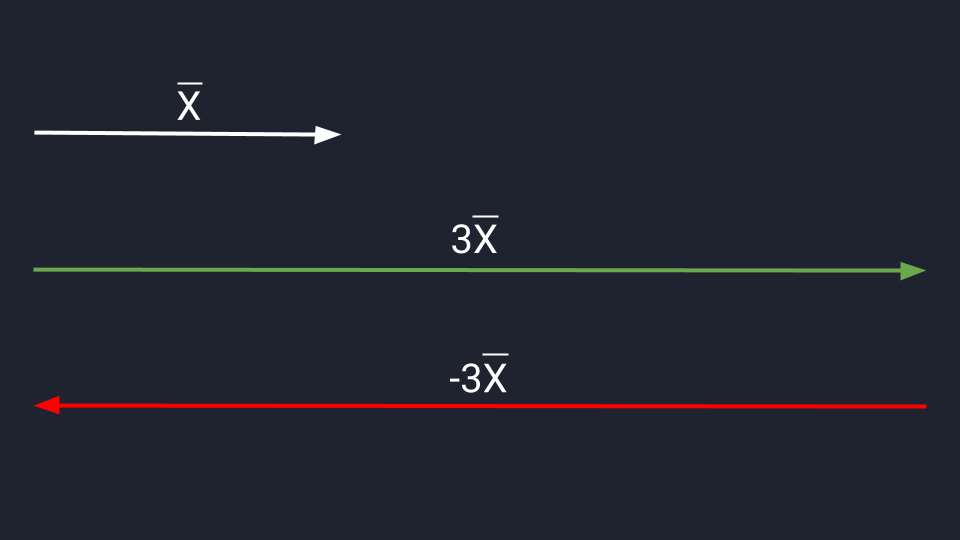
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
Умножение вектора на число
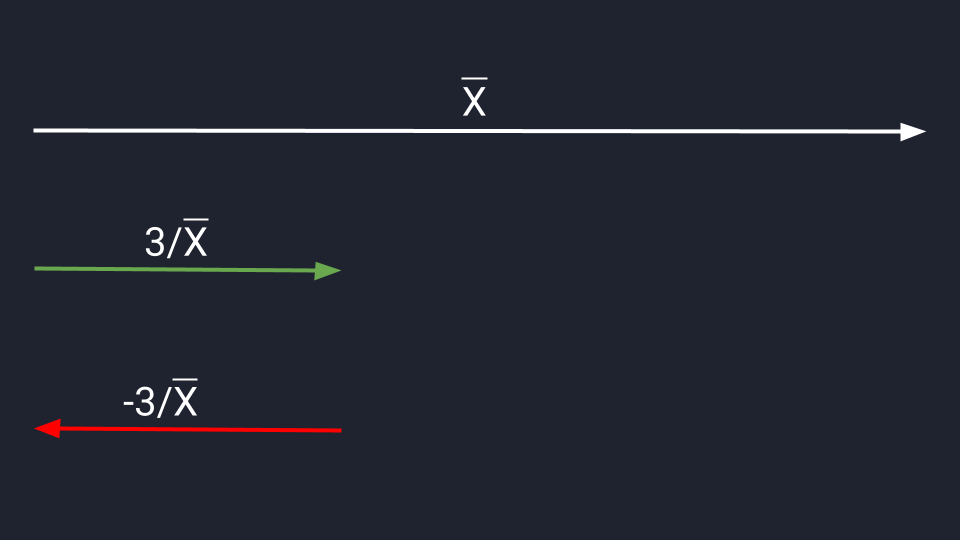
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
Деление вектора на число
Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.
Правила, по которым происходит сложение векторов
Как происходит сложение векторов, не всегда понятно ученикам. Дети не представляют того, что за ними скрывается. Приходится просто запоминать правила, а не вдумываться в суть. Поэтому именно о принципах сложения и вычитания векторных величин требуется много знаний.
В результате сложения двух и более векторов всегда получается еще один. Причем он всегда обязательно будет одинаковым, независимо от приема его нахождения.
Чаще всего в школьном курсе геометрии рассматривается сложение двух векторов. Оно может быть выполнено по правилу треугольника или параллелограмма. Эти рисунки выглядят по-разному, но результат от действия один.
Как происходит сложение по правилу треугольника?
Оно применяется тогда, когда векторы неколлинеарные. То есть не лежат на одной прямой или на параллельных.
В этом случае от некоторой произвольной точки нужно отложить первый вектор. Из его конца требуется провести параллельный и равный второму. Результатом станет вектор, исходящий из начала первого и завершающийся в конце второго. Рисунок напоминает треугольник. Отсюда и название правила.
Если векторы коллинеарные, то это правило тоже можно применять. Только рисунок будет расположен вдоль одной линии.
Как выполняется сложение по правилу параллелограмма?
До сих пор их было два. А как быть, если их 3 или 10? Использовать следующий прием.
Как и когда применяется правило многоугольника?
Если требуется выполнить сложение векторов, число которых — больше двух, пугаться не стоит. Достаточно последовательно отложить их все и соединить начало цепочки с ее концом. Этот вектор и будет искомой суммой.
Какие свойства действительны для действий с векторами?
О нулевом векторе. Которое утверждает, что при сложении с ним получается исходный.
О противоположном векторе. То есть о таком, который имеет противоположное направление и равное по модулю значение. Их сумма будет равна нулю.
О коммутативности сложения. То, что известно еще с начальной школы. Смена мест слагаемых не приводит к изменению результата. Другими словами, неважно какой вектор откладывать сначала. Ответ все равно будет верным и единственным.
Об ассоциативности сложения. Этот закон позволяет складывать попарно любые векторы из тройки и к ним прибавлять третий. Если записать это с помощью знаков, то получится следующее:
первый + (второй + третий) = второй + (первый + третий) = третий + (первый + второй).
Что известно о разности векторов?
Отдельной операции вычитания не существует. Это связано с тем, что оно, по сути, является сложением. Только второму из них задается противоположное направление. А потом все выполняется так, как если бы рассматривалось сложение векторов. Поэтому об их разности практически не говорят.
Для того чтобы упростить работу с их вычитанием, видоизменено правило треугольника. Теперь (при вычитании) второй вектор нужно отложить из начала первого. Ответом будет тот, что соединяет конечную точку уменьшаемого с ней же вычитаемого. Хотя можно и откладывать так, как было описано ранее, просто изменив направление второго.
Как найти сумму и разность векторов в координатах?
В задаче даны координаты векторов и требуется узнать их значения для итогового. При этом построений выполнять не нужно. То есть можно воспользоваться несложными формулами, которые описывают правило сложения векторов. Они выглядят так:
а (х, у, z) + в (k, l, m) = с (х+k, y+l, z+m);
Легко заметить, что координаты нужно просто сложить или вычесть в зависимости от конкретного задания.
Первый пример с решением
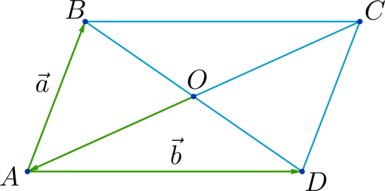
Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.
Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.
Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.
А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.
Ответ. Разность АО и ВО равна 8 см.
Второй пример и его подробное решение
Условие. У ромба АВСД диагонали равны 12 и 16 см. Точка их пересечения обозначена буквой О. Вычислите длину вектора, образованного разностью векторов АО и ВО.
Решение. Пусть обозначение вершин ромба будет таким же, как в предыдущей задаче. Аналогично решению первого примера получается, что искомая разность равна вектору АВ. А его длина неизвестна. Решение задачи свелось к тому, чтобы вычислить одну из сторон ромба.
Для этой цели потребуется рассмотреть треугольник АВО. Он прямоугольный, потому что диагонали ромба пересекаются под углом в 90 градусов. А его катеты равны половинам диагоналей. То есть 6 и 8 см. Искомая в задаче сторона совпадает с гипотенузой в этом треугольнике.
Ответ. Разность векторов АО и ВО составляет 10 см.
Третий пример с детальным решением
Условие. Вычислить разность и сумму двух векторов. Известны их координаты: у первого — 1 и 2, у второго — 4 и 8.
Решение. Для нахождения суммы потребуется сложить попарно первые и вторые координаты. Результатом будут числа 5 и 10. Ответом будет вектор с координатами (5; 10).
Четвертый пример
Условие. Длина вектора АВ равна 6 см, ВС — 8 см. Второй отложен от конца первого под углом в 90 градусов. Вычислить: а) разность модулей векторов ВА и ВС и модуль разности ВА и ВС; б) сумму этих же модулей и модуль суммы.
б) Сумма модулей векторов получается равной 14 см. Для поиска второго ответа потребуется некоторое преобразование. Вектор ВА противоположно направлен тому, который дан — АВ. Оба вектора направлены из одной точки. В этой ситуации можно использовать правило параллелограмма. Результатом сложения будет диагональ, причем не просто параллелограмма, а прямоугольника. Его диагонали равны, значит, модуль суммы такой же, как в предыдущем пункте.
Векторы: правила сложения и вычитания
Вектор \(\overrightarrow
\(\blacktriangleright\) Два вектора коллинеарны, если они лежат на одной прямой или на двух параллельных прямых.
В противном случае векторы называются неколлинеарными.
\(\blacktriangleright\) Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
Если их направления противоположны, то они называются противоположно направленными.
Правила сложения коллинеарных векторов:
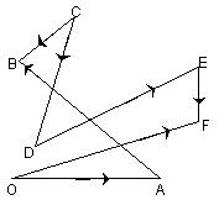
\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).
\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).
Правила сложения неколлинеарных векторов \(\overrightarrow \) и \(\overrightarrow\) :
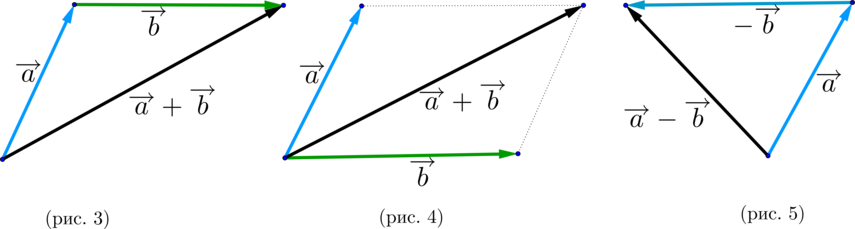
\(\blacktriangleright\) Правило треугольника (рис. 3).
\(\blacktriangleright\) Правило параллелограмма (рис. 4).
\[\begin
Старшеклассники, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение достойных баллов, обязательно должны повторить тему «Правила сложения и вычитания нескольких векторов». Как видно из многолетней практики, подобные задания каждый год включаются в аттестационное испытание. Если у выпускника вызывают трудности задачи из раздела «Геометрия на плоскости», к примеру, в которых требуется применить правила сложения и вычитания векторов, ему обязательно стоит повторить или вновь разобраться в материале, чтобы успешно сдать ЕГЭ.
Образовательный проект «Школково» предлагает новый подход в подготовке к аттестационному испытанию. Наш ресурс выстроен таким образом, чтобы учащиеся смогли выявить наиболее сложные для себя разделы и восполнить пробелы в знаниях. Специалисты «Школково» подготовили и систематизировали весь необходимый материал для подготовки к сдаче аттестационного испытания.
Для того чтобы задачи ЕГЭ, в которых необходимо применить правила сложения и вычитания двух векторов, не вызывали затруднений, мы рекомендуем прежде всего освежить в памяти базовые понятия. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Если вы уже вспомнили правило вычитания векторов и основные определения по данной теме, предлагаем закрепить полученные знания, выполнив соответствующие упражнения, которые подобрали специалисты образовательного портала «Школково». Для каждой задачи на сайте представлен алгоритм решения и дан правильный ответ. В теме «Правила сложения векторов» представлены различные упражнения; выполнив два-три сравнительно легких задания, учащиеся могут последовательно переходить к более сложным.
Оттачивать собственные навыки по таким, например, заданиям, как задачи на координатной плоскости, школьники имеют возможность в режиме онлайн, находясь в Москве или любом другом городе России. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
Покоординатное сложение векторов.
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
Правило параллелограмма. Сложение векторов по правилу параллелограмма.
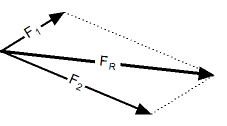
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
Правило треугольника. Сложение векторов по правилу треугольника.
Сложение векторов по правилу треугольника заключается в следующем:
Тригонометрический способ. Сложение векторов тригонометрическим способом.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team