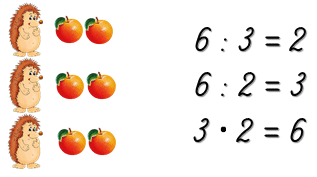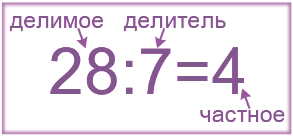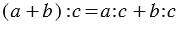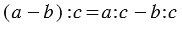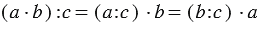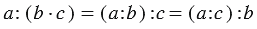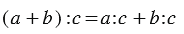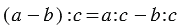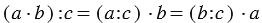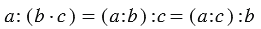Что получается в результате деления

Деление

В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.

Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.

Как ёжикам поделить между собой яблоки поровну?

Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.

Любой пример на умножение можно представить двумя примерами на деление.

Например, для выражения 6 • 4 = 24 есть два обратных выражения:

24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.

24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.

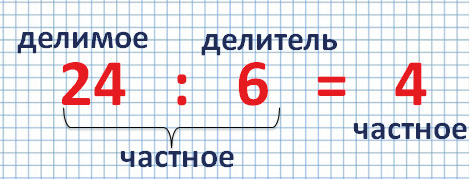
Числа при делении

При делении, как и при другом математическом действии, каждое число имеет свое название.

Число, которое делят, называется делимое.

Число, на которое делят, называется делитель.

Результат деления называется частное.

Чтение числовых выражений

Этот пример можно прочитать по-разному.

Деление на 1

Деление на 0

Деление числа само на себя

Связь деления и умножения

Чётные и нечётные числа

Числа, которые делятся на 2 без остатка, назы­ваются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.

Чётные: 6, 22 44, 60, 74, 82, 96

Нечётные: 7, 13, 21, 37, 45, 97

В несколько раз меньше

Для примера решим задачу:

В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?

Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.

Поделись с друзьями в социальных сетях:

Источник

Деление натуральных чисел

Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.

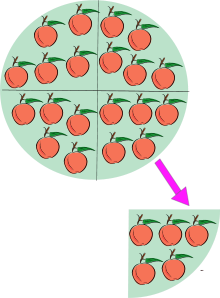
Рассмотрим задачу:

У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?

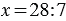
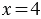
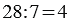
Данное действие записывают так: , или , где:

Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос «во сколько?», для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.

Из вышесказанного мы можем сделать вывод:

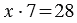
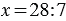
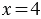
Пример: , следовательно, , то есть .

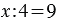
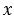
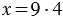
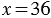
Пример: , по смыслу деления — это произведение 4 и 9, следовательно, , то есть .

Свойства деления

Распределительные свойства:

1. Деление суммы на число:

2. Деление разности на число:

3. Деление произведения на число:

4. Деление числа на произведение:

Действия с единицей и нулем

1. Деление числа на единицу: 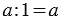то есть, при делении числа на единицу получается само число

2. Деление числа на себя: 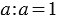, то есть при делении числа, не равного нулю, на само себя получается единица.

3. Деление нуля на число: 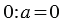, то есть при делении нуля на любое число, не равное нулю, получаем ноль.

НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!

Свойства деления

Распределительные свойства :

1. Деление суммы на число:

а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:

б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:

Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.

Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.

2. Деление разности на число:

Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?

а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:

б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:

Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.

3. Деление произведения на число:

В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?

а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:

б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:

б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:

Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.

Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.

4. Деление числа на произведение:

В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?

а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:

б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:

Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:

Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4

Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.

Действия с единицей и нулем

1. Деление числа на единицу:

У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?

Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:

2. Деление числа на себя:

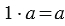
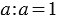
Из свойств умножения мы знаем, что: , а мы знаем, что по смыслу деления можно записать, что: , то есть при делении числа, не равного нулю, на само себя получается единица.

3. Деление нуля на число:

Рассуждая аналогично пункту 2 получаем: 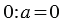, то есть при делении ноля на любое число, не равное нулю, получаем ноль.

Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!

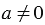
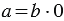
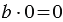
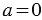
Это легко объяснить следующими рассуждениями: пусть мы взяли карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по карандашей в каждой коробке: , из смысла деления , в то же время мы знаем из свойств умножения, что: , то есть получаем, что , а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.

Поделись с друзьями в социальных сетях:

Источник

Деление (математика)

Деле́ние (операция деления) — одно из четырёх простейших арифметических действий, обратное умножению. Деление — это такая операция, в результате которой получается число (частное), которое при умножении на делитель даёт делимое. Существует несколько символов, используемых для обозначения оператора деления.

Подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание.

Рассмотрим, например, такой вопрос:

Сколько раз 3 содержится в 14?

Повторяя операцию вычитания 3 из 14, мы находим, что 3 «входит» в 14 четыре раза, и ещё «остаётся» число 2.

Результат деления также называют отношением.

Содержание

Деление натуральных чисел

Кольцо целых чисел не замкнуто относительно деления. Простым языком это означает то, что результат деления одного целого числа на другое может быть не целым. В случае, если всё-таки результат является целым числом, говорят о делении без остатка.

Деление чисел издавна считалось самой трудной из арифметических операций. В Средние века «секрет» деления знало не очень много посвящённых людей. Происходило это потому, что существовавшие алгоритмы деления были очень громоздки, сложны для исполнения и запоминания (например, деление в виде корабля (англ.) ). Появление деления столбиком радикально изменило эту ситуацию — теперь деление входит в раннюю школьную программу по математике наряду с остальными арифметическими действиями. Однако так же, как и в случае с умножением (см. быстрое умножение), в последнее время открыты более эффективные алгоритмы (см. en:Division (digital), применяющиеся в вычислительной технике.

Существуют правила, позволяющие быстро определить, делится ли число на заданный делитель без остатка (признаки делимости). Наиболее известные признаки делимости на 2, 3, 4, 5, 8, 9, 11, 25 и их производные, также существует признаки делимости на 7, 13, 1001 и другие числа.

Целое число, на которое одновременно делятся без остатка несколько чисел, называется их общим делителем.

Определение количества делителей натурального числа приводит к двум важным понятиям: составное и простое число. У простого числа есть ровно два различных делителя — 1 и само число. У составных чисел различных делителей больше двух. 1 не является ни составным, ни простым числом.

В случае, если одно натуральное число не делится на другое без остатка, можно говорить о делении с остатком. Рассмотрение остатков, их сравнение и формализация в виде вычетов привели к целой науке — теории чисел.

Обычно на остаток накладываются следующие ограничения (чтобы он был корректно, то есть однозначно, определён):

, ,

где — делимое, — делитель, — частное и — остаток.

Деление целых чисел

Деление произвольных целых чисел несущественно отличается от деления натуральных чисел — достаточно поделить их модули и учесть правило знаков.

Однако деление целых чисел с остатком определяется неоднозначно. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например, с остатком (-1)); в другом случае понятие остатка напрямую обобщается и ограничения заимствуются из натуральных чисел:

.

Деление рациональных чисел

Замыкание множества целых чисел по операции деления приводит к расширению его до множества рациональных чисел. Это приводит к тому, что результатом деления одного целого числа на другое всегда является рациональное число. Более того, полученные числа (рациональные) уже полностью поддерживают операцию деления (замкнуты относительно неё).

Правило деления обыкновенных дробей:

Деление вещественных чисел

Деление также замкнуто в поле ненулевых вещественных чисел. Дедекиндово сечение позволяет однозначно определить результат деления.

Деление комплексных чисел

Комплексные числа опять замкнуты относительно операции деления.

Деление в алгебре

В отличие от простейших арифметических случаев на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.

Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым (), так и правым (). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.

К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:

.

Отношение тензоров в общем случае не определено.

Деление многочленов

В общих чертах оно повторяет идеи деления натуральных чисел, ибо натуральное число есть не что иное, как значения многочлена, у которого коэффициенты — цифры, а вместо переменной стоит основание системы счисления:

.

Поэтому аналогично определяются: частное, делитель, делимое и остаток (с той лишь разницей, что ограничение накладывается на степень остатка). Поэтому к делению многочленов также применимо деление столбиком.

Отличие же заключается в том, что при делении многочленов основной упор делается на степени делимого и делителя, а не на коэффициенты. Поэтому обычно считается, что частное и делитель (а следовательно и остаток) определены с точностью до постоянного множителя.

Деление на ноль

По правилам стандартной арифметики деление на число 0 запрещено.

Другое дело — деление на бесконечно малую функцию или последовательность. Деление конечных функций на бесконечно малые приводит к появлению бесконечно больших, а отношение двух бесконечно малых называется неопределённостью 0/0, которую можно преобразовать (см. раскрытие неопределённостей) с тем, чтобы получить определённый результат.

Операции деления ненулевого числа на ноль не соответствует никакое действительное число.

Результат этой операции считается бесконечно большим и равным бесконечности:
, где
Смысл этого выражения состоит в том, что если делитель приближается к нулю, а делимое остается равным a или приближается к нему, то частное неограниченно увеличивается(по модулю).

Источник

Деление натуральных чисел

Подобно тому, как вычитание является обратным действием для сложения, так и для умножения существует свое обратное арифметическое действие.

Рассмотрим задачу. В школьной столовой раздали 90 яблок по 3 яблока каждому ученику класса. Сколько учеников учатся в этом классе?

Если бы нам было известно количество учеников в классе и количество яблок, которое получил каждый из них, то общее число яблок мы узнали бы, умножив число учеников на число яблок, доставшееся каждому. То есть, количество учеников – это первый сомножитель, количество яблок – второй сомножитель, а сколько яблок раздали – это произведение.

Деление – это арифметическое действие, которое состоит в нахождении одного из сомножителей при помощи данного произведения и второго сомножителя.

Делимое – это число, которое мы делим на другое. Это то самое произведение, которое нам дано.

Делитель – это число, на которое мы делим делимое. Это данный нам один из множителей.

Частное – это результат действия деление, то есть, искомый нами второй сомножитель.

На записи действие деление обозначается: двоеточием ( \(\textcolor <:>\) ), знаком обелюс ( \(\textcolor <\div>\) ), горизонтальной чертой или косой чертой ( \(\textcolor \) ).

Так, решение нашей задачи можно записать следующими способами:

При записи от руки действие деление принято записывать в виде двоеточия, обелюс применяется в печатной литературе, косая черта, которая по-другому называется слеш, – при записи на компьютере, а горизонтальная черта используется при записи деления в виде обыкновенной дроби.

Итак, разделить число a на число b – это значит найти такое число c, которое при умножении его на число b дает в результате числа a.
То есть: \(\textcolor \) , если \(\textcolor \) .

Компоненты действия деление:

Деление с остатком и неполное частное

К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( \(\textcolor <7\cdot 5=35>\) ), и у нас останется 2 яблока ( \(\textcolor <37-35=2>\) ).

Итак, деление с остатком – это нахождение такого наибольшего целого числа, умножив которое на делитель, мы получим число, максимально близкое к делимому, но не превосходящее его. Это искомое число называется неполное частное. Разница между делимым и неполным частным называется остаток.

Остаток всегда меньше делителя!

Связь деления с умножением, сложением и вычитанием

Когда мы выполняем находим произведение двух чисел, эти числа нам известны, а от нас требуется найти результат действия умножение. При делении (без остатка) нам известно произведение двух чисел, а найти нужно такое число, которое при умножении на известное данное число дает это самое произведение.

Следовательно, действие деление является обратным действию умножения.

Справедливо также и обратное, что действие умножение обратно действию деления. Таким образом:

Умножение и деление – это взаимно обратные действия.

Связь деления с умножением, а также со сложением и вычитанием прекрасно видна, если рассмотреть, как с помощью этих действий можно выполнить действие деление.

Деление двух чисел при помощи сложения

Деление двух чисел при помощи вычитания

То есть, 69 от 345 можно отнять 5 раз, поэтому \(\textcolor <349\div 69=5>\).

Деление двух чисел при помощи умножения

При помощи умножения узнать ответ на наш вопрос можно перебирая множитель числа 69 до тех пор, пока не получим заданное нам 345 :

Но эти три способа очень громоздки, особенно если частное представляет собой очень большое число. Их нужно знать только для того, чтобы понимать суть действия деления, суть тех задач, которые решаются посредством него.

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Прежде всего, нужно узнать количество цифр в частном и первое неполное делимое; как их находить, я подробно расписал в этой статье. В нашем случае первое неполное делимое равно 295 тысяч, а в частном будет 4 цифры.

Далее записываем известные компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру разряда тысяч, а под неполным делимым пишем результат произведения неполного частного и делителя. И сразу же находим остаток от этого действия, т.е. вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor <8\cdot 37=272>\). Записываем его под 295 и находим разницу: \(\textcolor <295-272=23>\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Рассмотрим еще один пример. \(\textcolor <25326\div 63>\).

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Итак, запомните, что каждое неполное делимое образует в частном одну цифру соответствующего разряда и что даже если неполное делимое меньше делителя, то в частном все равно нужно записать нулевой результат этого действия.

Итак, в общем виде алгоритм деления в столбик выглядит так:
1. Находим первое неполное делимое и количество цифр в частном.
2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.
3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.
4. Ставим между ними знак минус и выполняем действие.
5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.
6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.
7. Если неполное делимое невозможно разделить на делитель, то в частном ставится 0 и к этому неполному делимому сносится следующая цифра.

Деление на числа, заканчивающиеся нулями

Как и в случае с умножением, деление чисел облегчается, если делитель заканчивается одним или несколькими нулями. Рассмотрим два возможных случая:

Рассмотрим первый случай.

Деление на единицу с любым количеством нулей

Единица с любым количеством нулей – это не что иное как единица соответствующего разряда. Например, 10 – это 1 единица разряда десятков, 1000 – это одна единица разряда тысяч, 10000000 – 1 единица разряда десятков миллионов и т.д.

Запишите:
Чтобы разделить какое-нибудь число на единицу с любым количеством нулей, нужно отсчитать в делимом справа столько цифр, сколько нулей содержится в делителе; тогда все цифры, находящиеся слева от разделения, составят частное, а те, что справа – будут остатком.

Деление на число, оканчивающееся нулями

Рассмотрим на примере \(\textcolor <284556\div 2800>\).

Делитель здесь не что иное как 28 сотен. Логично предположить, что эти 28 сотен могут хотя бы один раз содержаться только в сотнях делимого. Значит, нам нужно определить, сколько в делимом всего единиц разряда сотен, и разделить их на 28 единиц разряда сотен делимого. А отброшенные цифры десятков и простых единиц добавятся к остатку.

Запишите:
Чтобы разделить какое-нибудь число на число, заканчивающееся нулями, нужно отбросить мысленно нули в делителе, в делимом тоже отбросить мысленно такое же количество цифр, как и нулей в делителе. Получившееся число в делимом разделить на получившееся число в делителе, а к остатку прибавить (снести) те цифры делимого, которые отбросили ранее.

Проверка деления

Так как делимое – это делитель, умноженный на частное и плюс остаток, что следует из определения деления, то результат выполнения деления можно проверить умножением.

Если в результате действия деления не получилось остатка, то деление можно проверить и делением. Действительно, если делимое – это произведение делителя и частного, то разделив делимое на частное (один из сомножителей), мы должны получить второй сомножитель, то есть, делитель.

Свойства деления

Свойства деления я представлю двумя группами:

Давайте рассмотрим каждую группу подробнее.

Действия деления с единицей и нулем

При делении числа на единицу получается то же самое число.

Действительно, разделить число на единицу означает узнать, сколько единиц содержится в данном числе. А количество единиц в числе – это не что иное, как само это число.

И ли вот, например, если 10 яблок нужно раздать одному человеку ( 10 поделить на 1 ), то ему все эти 10 яблок и достанутся, правда?

При деление одинаковых чисел (числа на равное число) в результате будет 1 (единица).

В самом деле, если все единицы какого-то числа разделить на количество частей, равное количеству единиц этого числа, то в каждая часть получит по 1 единице.

Например, если 20 яблок раздать 20 школьникам, то каждому достанется по 1 яблоку.

При делении нуля на любое число, отличное от нуля, в результате будет нуль.

Разделить нуль на число означает найти такое число, умножив которое на данный делитель, мы получим в результате нуль. А такое число только одно – это нуль.

На нуль делить нельзя, то есть, нуль не может выступать в роли делителя.

При делении каких угодно чисел делителем может быть любое число, кроме нуля.

Рассмотрим два случая: когда нулём является только делитель, и когда делимое и делитель оба нули.

Распределительные свойства деления

Чтобы найти частное от деления суммы на число, нужно поделить каждое слагаемое на это число, и найти сумму полученных частных.
\(\textcolor <(a+b+c)\div d=a\div d+b\div d+c\div d>\).
При этом подразумевается, что все действия деления получаются без остатка.

Чтобы найти частное от деления разности на число, нужно поделить на это число отдельно сперва уменьшаемое, а потом вычитаемое, после чего найти разность первого частного и второго.
\(\textcolor <(a-b)\div c=a\div c-b\div c>\)
При этом также предполагается, что при делениях уменьшаемого и вычитаемого на число не получается остатков.

Например: \[\textcolor <(36-24)\div 6=36\div 6-24\div 6=6-4=2>\] Число 36 состоит из 6 шестерок, а 24 – из 4 шестерок, а забрав у 6 шестерок 4 шестерки, получим 2 шестерки. Такой же итог будет и если мы сперва у 36 отнимем 24 единицы (останется 12 ), а потом найдем, сколько в этой разнице содержится шестерок: \(\textcolor <12\div 6=2>\).

Чтобы найти частное от деления произведения на число, нужно поделить на него только один из сомножителей, а результат умножить на неизмененные остальные.
\(\textcolor <(a\cdot b\cdot c)\div d=a\div d\cdot b\cdot c=b\div d\cdot a\cdot c=c\div d\cdot a\cdot b>\).

Чтобы найти частное от деления числа на произведение, нужно это число поделить на первый сомножитель, результат деления поделить на второй сомножитель, полученное частное – на третий и так далее.
\(\textcolor \).
При этом предполагается, что при всех этих делениях не получается остатков.

На рисунке наглядно видно, что в итоге после применения этого правила, число 30 получилось разделенным на 6 равных частей.

Изменение частного при изменении делимого и делителя

При рассмотрении изменений частного в результате изменений делимого и делителя предполагается, что действие деление происходит без остатка. В противном случае изменения могут быть не такими, о которых идет речь ниже.

При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.

Если мы в примере \(\textcolor <24\div 4=6>\) делимое увеличим, к примеру, в 3 раза, то мы можем переписать это выражение в виде \(\textcolor <(24+24+24)\div 4>\). Используя свойство деления суммы на число, мы увидим, что теперь нам нужно сложить три слагаемых, каждое из которых равно начальному выражению: \(\textcolor <24\div 4+24\div 4+24\div4>\). Отсюда очевидно, что результат будет больше начального в 3 раза.

Если мы в этом же примере \(\textcolor <24\div 6>\) уменьшим делимое в 3 раза, то есть, разделим его на три равные части, то очевидно, что результат деления одной части на 6 будет в 3 раза меньше, чем результат деления трех таких же частей. Посмотрите сами. Начальное выражение \(\textcolor <24\div 6>\) можно записать в виде: \(\textcolor <(8+8+8)\div 6=8\div 6+8\div 6+8\div 6>\), а уменьшенное в 3 раза делимое даст нам только одно из трех таких слагаемых: \(\textcolor <8\div 6>\).

При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.

Действительно, изменение делителя означает, что делимое необходимо разделить на большее или меньшее количество равных частей. Соответственно, если нужно разделить на большее число частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее число частей, то каждая часть будет крупнее.

В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.

При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.

Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось это, или нет.

Источник