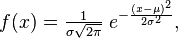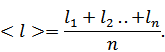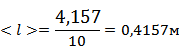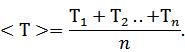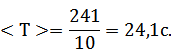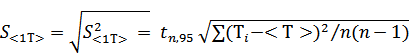Что понимается под измерением физической величины
Опыт №2



Лабораторная работа №1
Тема: «Оценка погрешностей прямых и косвенных измерений при изучении колебаний математического маятника»
Цель работы: вычисление средних значений измеряемых величин и доверительного интервала прямых и косвенных измерений при заданной доверительной вероятности.
Приборы и принадлежности:математический маятник, секундомер, линейка.
Схема экспериментальной установки приведена на Рис. 1
Рис. 1 Экспериментальная установка
Где 1 – штатив, 2 – подвес, 3 – стойка, 4 – грузик, 5 – основание, l – длина подвеса.
Теория
1) Что понимается под измерением физической величины? Что такое прямые и косвенные измерения?
где х – отвлечённое число, которое показывает сколько раз единица измерения содержится в измеряемой величине.
Прямые измерения – это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных, с помощью измерительных приборов.
Косвенные измерения – это измерения, при которых искомую величину y вычисляют по результатам прямых измерений, связанных с искомой функциональной зависимостью y=f(x), т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. (Косвенные измерения производятся, когда искомую величину невозможно или сложно измерить или когда прямое измерение даёт менее точный результат).
2) Дать определение основным видам погрешностей. Привести примеры.
Систематические погрешности – это ошибки, являющиеся следствием неправильной калибровки прибора (сбитый ноль, их тепловое расширение), ошибочности метода измерений и т.п. При наличии таких погрешностей измеренное значение отклоняется от истинного значения в одну и ту же сторону, на одну и ту же величину. Повторными измерениями эти ошибки не уменьшаются, но их можно оценить сравнением результатов измерений с измерениями, полученными исправным прибором (с большей степенью точности).
Случайные погрешности вносятся изменчивыми условиями эксперимента, несовершенством органов чувств, ограниченной точностью измерений и т.п. Случайные ошибки подчиняются законам теории вероятности и математической статистики. Чаще всего они проявляются в виде разброса показаний прибора. В результате этого разброса измеряемая величина случайным образом отклоняется от истинного значения в произвольную сторону на произвольную величину.
Промахи – ошибки (погрешности), чаще всего возникающие вследствие невнимательности человека или недостаточной его квалификации и опыта. Их можно наблюдать, например, при неправильном отсчёте измеряемого значения (неправильное определение цены деления прибора). Также к ним могут привести внезапные внешние влияния на измерительное устройство.
3) Как определяются абсолютная и относительная ошибки отдельного результата измерения и совокупности измерений?
Относительная ошибка вычисляется по формуле:
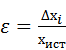
4) Описать Гауссову функцию распределения плотности случайной величины. Связать её параметры со средним значением и дисперсией выборки.
Распределение Гаусса ( Нормальное распределение) — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:
где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.
Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в статье «Многомерное нормальное распределение».
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.
5) Что такое дисперсии среднего значения и среднеквадратичного отклонения и как они находятся при прямых измерениях величины?
Рассмотрим основы теории случайных погрешностей, позволяющей оценить величину погрешности для серии опытов. Закономерности, связанные со случайными величинами, изучаются теорией вероятности и математической статистикой.
Допустим, что было произведено N независимых наблюдений некоторой физической величины х. Обозначим через xi (i=1,N) результаты этих наблюдений. Наилучшей оценкой истинного значения xis по этим результатам является их среднее арифметическое значение:
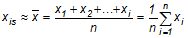 , , |
«Разброс» величины около ее среднего значения при одинаковых 
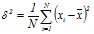 , , |
Корень квадратный из дисперсии называется стандартным или среднеквадратичным отклонением
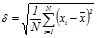 , , |
Среднеквадратическое отклонение и дисперсия при данных условиях и процедуре измерений являются величинами постоянными и характеризуют степень влияния случайных погрешностей на результаты измерения: чем меньше они, тем точнее проведены измерения. Обработка результатов серии измерений сводится к возможно более точному нахождению 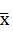

Если «разброс» δизмеряемой величины х при большом числе измерений N есть величина статистически постоянная, то можно ожидать, что в произвольно заданный интервал Δх будет попадать более или менее постоянное число n измерений, зависящее от того, где на числовой оси х выбрать Δх.
6) Что такое доверительный интервал и доверительная вероятность и как записывается окончательный результат измерений?
Доверительный интервал – термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Метод доверительных интервалов разработал американский статистик Ежи Нейман, исходя из идей английского статистика Рональда Фишера.
Доверительная вероятность – вероятность того, что полученная при измерении оценка абсолютно точно совпадает с истинным значением параметра, равна нулю. Однако можно поставить вопрос, например, такой. Пусть получено некоторое измеренное значение; так вот, каков должен быть интервал, чтобы истинное значение оказалось внутри него с вероятностью, скажем, 0.9. Или 0.99. Исследователь выбирает эту вероятность сам. Ясно, что чем выше вероятность, тем шире интервал. Вот эти вероятности и соответствующие им интервалы называются доверительными.
7) Каков физический смысл ускорения свободного падения?
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил. В соответствии с уравнением движения тел в неинерциальных системах отсчёта ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «Же») варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет g = 9,80665 м/с². Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81; 9,8 или 10 м/с².
Упр.1.Измерение длины математического маятника.
| N | ∑ | ||||||||||
| li (м) | 0,415 | 0,414 | 0,413 | 0,415 | 0,414 | 0,416 | 0,420 | 0,417 | 0,418 | 0,415 | 4,157 |
| (l- ) 2 (мм) | 0,49 | 2,89 | 7,29 | 0,49 | 2,89 | 0,09 | 18,49 | 1,69 | 5,29 | 0,49 | 40,1 |
1) Находим среднее длины по формуле
2) Находим среднеквадратичное отклонение длины маятника, обусловленное случайными ошибками, по формуле
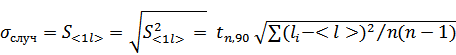
где 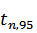
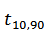
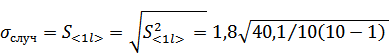
3) Вычисляем среднеквадратичное отклонение, обусловленное приборной ошибкой по формуле 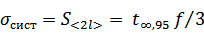
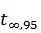
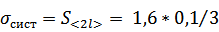
4) Вычисляем абсолютную ошибку по формуле
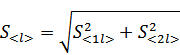
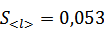
1. Так как 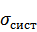
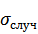
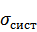
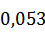
2. Запишем результат измерения в виде l = ±∆ l:
3. Вычислим относительную ошибку измерения:
Е = 0,053/385,6 *100% = 0,014%
Результат измерения 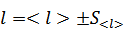
Опыт №2
Определение периода колебаний математического маятника.
| N | ∑ | ||||||||||
| Тi (с) | 24,5 | 24,5 | |||||||||
| (Т- ) 2 | 0,81 | 0,01 | 0,01 | 0,16 | 0,81 | 1,21 | 0,16 | 0,01 | 0,01 | 1,21 | 4.4 |
1) Находим среднее длины по формуле
2) Находим среднеквадратичное отклонение длины маятника, обусловленное случайными ошибками, по формуле
где 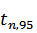
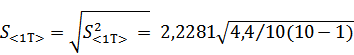
3) Вычисляем среднеквадратичное отклонение, обусловленное приборной ошибкой по формуле 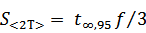
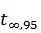
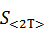
4) Вычисляем абсолютную ошибку по формуле
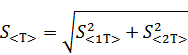
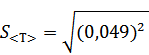
Результат измерения: 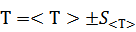
Т= (24,1 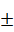
Измерение
Измерение — совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).
Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:
В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая, или не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам, например, Шкала Рихтера интенсивности землетрясений, Шкала Мооса — шкала твёрдости минералов.
Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.
Содержание
Классификация измерений
По видам измерений
Согласно РМГ 29-99 «Метрология. Основыне термины и определения» выделяют следующие виды измерений:
Также стоит отметить, что в различных источниках дополнительно выделяют таки виды измерений: метрологически и технические, необходимые и избыточные и др.
По методам измерений
По условиям, определяющим точность результата
По отношению к изменению измеряемой величины
Статические и динамические.
По результатам измерений
Классификация рядов измерений
По точности
По числу измерений
Классификация измеряемых величин
По точности
По результатам измерений
История
Единицы и системы измерения
См. также
Примечания
Литература и документация
Литература
Нормативно-техническая документация
Ссылки
Полезное
Смотреть что такое «Измерение» в других словарях:
ИЗМЕРЕНИЕ — представление свойств реальных объектов в виде числовой величины, один из важнейших методов эмпирического познания. В самом общем случае величиной называют все то, что может быть больше или меньше, что может быть присуще объекту в большей или… … Философская энциклопедия
Измерение X — Измерение Икс … Википедия
измерение — замер, обмер; вымеривание, установление, фиксирование, замеривание, распознавание, промер, диагностирование, смеривание, нахождение, обмеривание, определение Словарь русских синонимов. измерение см. установление 2 Словарь синонимов … Словарь синонимов
измерение — (в психологии) научный метод представления числами интересующего психического свойства или параметров психического процесса на основе нек рых процедурных правил. Совокупность теоретико математических представлений и процедурных правил,… … Большая психологическая энциклопедия
ИЗМЕРЕНИЕ — ИЗМЕРЕНИЕ, измерения, ср. 1. Действие по гл. измерить измерять. Измерение роста. 2. Измеряемая величина, протяжение (мат.). Куб имеет три измерения: длину, высоту и ширину. ❖ Четвертое измерение (ирон.) перен. сверхъестественная и бесплодно… … Толковый словарь Ушакова
ИЗМЕРЕНИЕ — последовательность эксперим. и вычислит. операций, осуществляемая с целью нахождения значения физ. величины, характеризующей нек рый объект или явление. И. завершается определением степени приближения найденного значения к истинному значению… … Физическая энциклопедия
ИЗМЕРЕНИЕ — ИЗМЕРЕНИЕ, действия, производимые с целью нахождения числовых значений какой либо величины в принятых единицах измерения. Измерение выполняют с помощью соответствующих средств измерения (линейка, часы, весы и т.д.). Различают прямые… … Современная энциклопедия
ИЗМЕРЕНИЕ — совокупность действий, выполняемых при помощи средств измерений с целью нахождения числового значения измеряемой величины в принятых единицах измерения. Различают прямые измерения (напр., измерение длины проградуированной линейкой) и косвенные… … Большой Энциклопедический словарь
измерение — Сравнение конкретного проявления измеряемого свойства (измеряемой величины) со шкалой (частью шкалы) измерений этого свойства (величины) с целью получения результата измерения (значения величины или оценки свойства). [МИ 2365 96] измерение… … Справочник технического переводчика
Измерение — ИЗМЕРЕНИЕ, действия, производимые с целью нахождения числовых значений какой либо величины в принятых единицах измерения. Измерение выполняют с помощью соответствующих средств измерения (линейка, часы, весы и т.д.). Различают прямые… … Иллюстрированный энциклопедический словарь
Физические величины. Измерение физических величин. Точность и погрешность измерений
Цели урока:
1) Обучающая: обеспечить формирование у учащихся представлений о физической величине, обеспечит усвоение учащимися теоретических знаний об основных характеристиках физической величины, познакомить учащихся с простейшими измерительными приборами, научить определять цену деления и точность отсчета при использовании различных шкал.
2) Развивающая: способствовать расширению кругозора учащихся о физике; умение находить некоторые закономерности; развитие памяти, самостоятельного суждения.
3) Воспитывающая: интерес, любознательность, наблюдательность, аккуратность в записях.
Ход урока:
1. Организационный этап.
Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний
Прежде чем начинать наш с вами уже второй урок в курсе Физики, хотелось бы вспомнить то, о чем мы говорили на предыдущем занятии.
Мы ввели понятие «Физическое тело». Что же это? Это любой предмет, окружающего нас мира.
Физическое явление — все изменения, которые происходят с физическими полями и телами.
Для описания физических тел и физических явлений используют физические величины.
Например, для описания деревянного бруска нам необходимо использовать такие физические величины как масса, длина, ширина, высота, объем.
Откройте тетради и запишите число и тему нашего урока.
3. Этап получения новых знаний.
Для описания физических тел и физических явлений используют физические величины.
Например, для описания деревянного бруска нам необходимо использовать такие физические величины как масса, длина, ширина, высота, объем.
То есть физическая величина это то, что мы можем измерить. Измеряемое свойство тела или явления.
Каждая физическая величина имеет название, например масса; Буквенное обозначение (массу обозначают латинской буквой эм), способ измерения (с помощью весов), числовое значение (например, масса человека равна 45), и единицы измерения (кг). Получаем, масса тела равна 45 кг.
Для каждой физической величины приняты свои единицы измерения. Для удобства все страны мира стремятся пользоваться одинаковыми единицами измерения физических величин. С 1963 года во многих странах мира используется Международная система единиц — СИ (система интернациональная). В этой системе основной единицей длины является метр, времени — секунда, массы — килограмм.
Существует единицы, которые в 10, 100, 1000 раз больше принятых. Такие единицы называет кратными, и именуются с соответствующими греческими приставками. Например, десяти соответствует приставка «дека», стам — «гекто», тысячи — «кило».
Если используют единицы, которые в 10, 100, 1000 раз меньше принятых единиц (это дольные единицы), то используют приставки, взятые из латинского языка. «Деци» — ноль целых одна десятая, «санти» — ноль целых одна сотая, «милли» — ноль целых одна тысячная.
Измерения очень важны в нашей жизни, для их проведения необходимы измерительные приборы. Самые простые приборы для измерения длины линейка, рулетка, мерная лента.
Для измерения объема жидкости мензурка, мерный цилиндр, мерная колба.
Для измерения температуры используют комнатный, водный, медицинский термометры. Медицинский, в свою очередь, бывает электронный и ртутный.
Существуют и другие измерительные приборы. Например, времени секундомер, часы. Силы — динамометр. Давления, атмосферного — барометр, газов в сосуде — манометр.
Приборы делят на шкальные и цифровые. Каждый шкальный прибор имеет шкалу и цену деления.
Шкала измерительного прибора называют совокупность отметок и цифр на отсчетном устройстве прибора, соответствующая ряду последовательных значений измеряемой величины
Цена деления — значение наименьшего деления шкалы прибора.
Для определения цены деления шкалы нужно от большего числа, соответствующего какому — либо делению шкалы, вычесть меньшее и полученную разность поделить на число делений между цифрами. Получаем 0,1 сантиметра на деление.
Какой же прибор точнее, цена деления которого меньше или больше?
Рассмотрим мерную ленту А) и линейку б). У обоих приборов единицы измерения совпадают!
Для нахождения цены деления мерной ленты возьмем два рядом стоящих значения на шкале, от большего вычтем меньшее и разделим на количество делений между данными цифрами. Получим, 1 сантиметр на деление.
Также определим цену деления для линейки. Количество делений в данном случае 10. Получим, ноль целых одна десятая сантиметра на деление.
Точнее тот прибор у которого цена деления меньше. Значит данная линейка точнее мерной ленты.
То есть, имея меньшую цену деления, мы меньше ошиблись.
Чему же равна погрешность измерительных приборов?
Погрешность равна половине цены деления.
Например, погрешность при измерении температуры равна половине цены деления данного термометра.
Найдем ее: для этого определим цену деления термометра.
Берем два любых значения, например 20 и 10, от большего вычтем меньшее значение и разделим на количество делений между ними, их пять. Получили, что она равна 2 градуса на деление.
Значит погрешность равна 1 градус.
Как же это записать?
T = 20±1 C, где 20 — показания термометра, 1 — погрешность, знак полюс минус использует потому, что ошибиться можно как в большую так и в меньшую сторону.
При записи величин с учетом погрешности следует пользоваться формулой, где
А — измеряемая величина,
а — результат измерений,
Так что же значит измерить физическую величину?
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
Например, чтобы измерить длину отрезка прямой между точками, А и В, надо приложить линейку и по шкале определить сколько сантиметров укладывается между данными точками.
Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямыми. Например, измерение длины бруска, ширины или высоты бруска.
А как же определить объем этого самого бруска. Конечно же, используя формулу. Объем есть произведение длины, ширины и высоты.
В этом случае, когда физическую величину (объем), определили по формуле, говорят, что измерения провели косвенно.
3. Этап обобщения и закрепления нового материала.
Итак, сделаем основные выводы:
— Физическая величина — измеряемое свойство тела или явления
— Каждый шкальный прибор имеет шкалу и цену деления
— Шкала измерительного прибора — это совокупность отметок и цифр на отсчетном устройстве прибора, соответствующая ряду последовательных значений измеряемой величины
— Цена деления (С) — значение наименьшего деления шкалы прибора
— Для определения цены деления шкалы нужно от большего числа, соответствующего какому- либо делению шкалы, вычесть меньшее и, разность поделить на число делений между цифрами
— Погрешность измерительных приборов равна половине цены деления
Для закрепления, изученного материала, ответим на ряд вопросов.
Что такое физическая величина? Какие основные физические величины входят в систему СИ? Какие шкальные измерительные приборы вам известны? Какие цифровые измерительные приборы вам известны? Перечислите приборы для измерения длины, времени, температуры. Что такое цена деления? Как определить цену деления прибора? От чего зависит точность измерения? Что необходимо учитывать при выборе измерительного прибора? Чем отличаются кратные и дольные единицы? Что значит измерить косвенно или прямым способом?
4. Рефлексия.
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
5. Домашнее задание: § 4- 5.
1. Из перечисленных приборов выбрать а) шкальные, б) цифровые.
Линейка, весы электронные, напольные (не электронные весы), секундомер, часы наручные механические, часы электронные настенные, динамометр, мензурка, мерный стаканчик, барометр, манометр.
2. Определить цену деления данного прибора.
3. Определить цену деления данного термометра.
4. Определить цену деления и погрешность данной линейки.
5. Какая из данных мерных лент более точная? Почему? Чем точнее можно измерить длину стола линейкой или мерной лентой? Почему?