Что понимается под множеством

Множество и его элементы. Подмножества

Понятие множества

Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».

Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».

Приведём примеры множеств:

Множество людей в салоне самолёта

Множество деревьев в парке

Множество планет Солнечной системы

Множество электронов в атоме

Множество натуральных чисел

Множество «синих-синих презелёных красных шаров»

Конечное, бесконечное и пустое множества

Людей в салоне самолёта легко посчитать, это множество конечно.

С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.

Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.

Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.

Помидоры на грядке

Числа (натуральные, рациональные, действительные и т.д.)

Количество рациональных чисел на отрезке [0;1]

Полосатые летающие слоны

Все точки пересечения двух параллельных прямых на плоскости

Способы задания множеств

1) Перечисление – в списке задаются все элементы множества.

Множество всех континентов Земли:

Множество букв слова «математика»:

Множество натуральных чисел меньших 5:

2) Характеристическое свойство – указывается особенность элементов множества.

D = – множество всех материков планеты Земля

3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)

Подмножества

Говорят, что B содержит A, или B покрывает A.

Пустое множество является подмножеством любого множества.

Множество людей является подмножеством приматов, живущих на Земле.

Множество квадратов является подмножеством прямоугольников.

Множество всех подмножеств данного множества A называют булеаном или степенью множества A.

Примеры

Пример 1. Запишите данное множество с помощью перечисления элементов:

Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:

Задано множество целых чисел, модуль которых не больше 3. Перечисляем:

Задано множество рациональных чисел, являющихся корнями уравнения

(x-1)(2x+5) = 0. Перечисляем:

Пример 2. Запишите данное множество с помощью характеристического свойства:

а) Множество всех натуральных чисел меньше 10

б) Множество всех действительных чисел, кроме 0

в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1

Пример 3. Изобразите на графике в координатной плоскости данное множество:

Задано конечное множество точек, которое можно представить перечислением:

Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:

Источник

Значение слова «множество»

2. Мат. Совокупность элементов, объединенных по какому-л. признаку. Теория множеств.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть несводимое к другим понятиям, а значит, и не имеющее определения; для его объяснения используются описательные формулировки, характеризующие множество как совокупность различных элементов, мыслимое как единое целое. Также возможно косвенное определение через аксиомы теории множеств. Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством.

МНО’ЖЕСТВО, а, ср. (книжн.). 1. только ед. Неопределенно большое количество, число чего-н. М. рабочих. М. фактов. Я слышал в жизни множество отличнейших певцов. Нкрсв. 2. Совокупность элементов, выделенных в обособленную группу по какому-н. признаку (мат.). Конечное, бесконечное м. Эквивалентные множества.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

мно́жество

2. матем. совокупность, результат объединения объектов по определённому признаку, свойству ◆ По определению, пустое множество также относят к классу перечислимых. В. А. Успенский, «Алгоритм», 2002 г. (цитата из НКРЯ) ◆ Например, подмножеств множества натуральных чисел бесконечно много, и самих натуральных чисел бесконечно много. И. В. Ященко, «Парадоксы теории множеств», 2002 г. (цитата из НКРЯ)

3. матем. универсальная алгебра вырожденная алгебраическая система с пустым набором операций и отношений

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: светильня — это что-то нейтральное, положительное или отрицательное?

Источник

Множества: понятие, определение, примеры

Множеством называется собрание, совокупность, коллекция вещей, объединенных по какому-либо признаку или по какому-либо правилу. Понятие множества возникает путем абстракции. Рассматривая какую-либо совокупность предметов как множество, отвлекаются от всех связей и соотношений между различными предметами, составляющими множества, но сохраняют за предметами их индивидуальные черты. Таким образом, множество, состоящее из пяти монет, и множество, состоящее из пяти яблок, — это разные множества. С другой стороны, множество из пяти монет, расположенных по кругу, и множество из тех же монет, положенных одна на другую, — это одно и то же множество.

Приведем несколько примеров множеств. Можно говорить о множестве песчинок, составляющих кучу песка, о множестве всех планет нашей солнечной системы, о множестве всех людей, находящихся в данный момент в каком-либо доме, о множестве всех страниц этой книги. В математике тоже постоянно встречаются различные множества, например множество всех корней заданного уравнения, множество всех натуральных чисел, множество всех точек на прямой и т. д.

Математическая дисциплина, изучающая общие свойства множеств, т. е. свойства множеств, не зависящие от природы составляющих их предметов, называется теорией множеств. Эта дисциплина начала бурно развиваться в конце XIX и начале XX в. Основатель научной теории множеств — немецкий математик Г. Кантор.

Работы Кантора по теории множеств выросли из рассмотрения вопросов сходимости тригонометрических рядов. Это весьма обычное явление: очень часто рассмотрение конкретных математических задач ведет к построению весьма абстрактных и общих теорий. Значение таких абстрактных построений определяется тем, что они оказываются связанными не только с той конкретной задачей, из которой они выросли, но имеют приложения и в ряде других вопросов. В частности, именно так обстоит дело и с теорией множеств. Идеи и понятия теории множеств проникли буквально во все разделы математики и существенно изменили ее лицо. Поэтому нельзя получить правильного представления о современной математике, не познакомившись с элементами теории множеств. Особенно большое значение имеет теория множеств для теории функций действительного переменного.

Множество считается заданным, если относительно любого предмета можно сказать, принадлежит он множеству или не принадлежит. Иными словами, множество вполне определяется заданием всех принадлежащих ему предметов. Если множество \(M\) состоит из предметов \(a,\,b,\,c,\,\ldots\) и только из этих предметов, то пишут

Объединение или сумма множеств

При этом, даже если элемент \(x\) принадлежит нескольким слагаемым, то он входит в сумму \(M\) лишь один раз. Ясно, что

Пересечение множеств

Читателю рекомендуется доказать, что сумма и пересечение множеств связаны обычным распределительным законом

Разность множеств

Нетрудно показать, что всегда

Таким образом, правила действий над множествами значительно отличаются от обычных правил арифметики.

Конечные и бесконечные множества

Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.

Рассмотрим два каких-либо множества \(M\) и \(N\) и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.

Однако, если оба множества \(M\) и \(N\) бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.

Взаимно однозначное соответствие множеств

Пусть в зале находится некоторое число людей и некоторое число стульев. Чтобы узнать, чего больше, достаточно попросить людей занять места. Если кто-нибудь остался без места, значит, людей больше, а если, скажем, все сидят и заняты все места, то людей столько же, сколько стульев. Описанный способ сравнения количества элементов во множествах имеет то преимущество перед непосредственным счетом элементов, что он без особых изменений применяется не только к конечным, но и к бесконечным множествам.

Рассмотрим множество всех натуральных чисел

Какое множество содержит больше элементов? На первый взгляд кажется, что первое. Однако мы можем образовать из элементов этих множеств пары, как указано ниже.

Ни один элемент \(M\) и ни один элемент \(N\) не остается без пары. Правда, мы могли бы также образовать пары и так:

Тогда многие элементы из \(M\) остаются без пар. С другой стороны, мы могли бы составить пары и так:

Таким образом, мы получили ответ на один из поставленных выше вопросов: как сравнивать между собой количество элементов в бесконечных множествах. Однако это нисколько не приблизило нас к ответу на другой вопрос: существуют ли вообще бесконечные множества. имеющие различные мощности? Чтобы получить ответ на этот вопрос, исследуем некоторые простейшие типы бесконечных множеств.

Счетные множества. Если можно установить взаимно однозначное соответствие между элементами множества \(A\) и элементами множества всех натуральных чисел

Таблица 1 показывает, что множество всех четных чисел счетно (верхнее число рассматривается теперь как номер соответствующего нижнего числа).

Счетные множества это, так сказать, самые маленькие из бесконечных множеств: во всяком бесконечном множестве содержится счетное подмножество.

Если два непустых конечных множества не пересекаются, то их сумма содержит больше элементов, чем каждое из слагаемых. Для бесконечных множеств это правило может и не выполняться. В самом деле, пусть \(G\) есть множество всех четных чисел, \(H\) — множество всех нечетных чисел и \(Z\) — множество всех натуральных чисел. Как показывает таблица 4, множества \(G\) и \(H\) счетны. Однако множество \(Z=G+H\) вновь счетно.

Нарушение правила «целое больше части» для бесконечных множеств показывает, что свойства бесконечных множеств качественно отличны от свойств конечных множеств. Переход от конечного к бесконечному сопровождается в полном согласии с известным положением диалектики — качественным изменением свойств.

Здесь в первой строке помещены все натуральные числа в порядке их возрастания, во второй строке 0 и целые отрицательные числа в порядке их убывания, в третьей строке — положительные несократимые дроби со знаменателем 2 в порядке их возрастания, в четвертой строке — отрицательные несократимые дроби со знаменателем 2 в порядке их убывания и т. д. Ясно, что каждое рациональное число один и только один раз находится в этой таблице. Перенумеруем теперь
все числа этой таблицы в том порядке, как это указано стрелками. Тогда все рациональные числа разместятся в порядке одной последовательности:

Этим установлено взаимно однозначное соответствие между всеми рациональными числами и всеми натуральными числами. Поэтому множество всех рациональных чисел счетно.

Множества мощности континуума

Из рис. 1 видно, что множество точек любого отрезка \(AB\) имеет мощность континуума. Здесь взаимно однозначное соответствие устанавливается геометрически, посредством проектирования.

Нетрудно показать, что множества точек любого интервала \(x\in[a,b]\) и всей числовой прямой \(x\in[-\infty,+\infty]\) — имеют мощность континуума.

Значительно более интересен такой факт: множество точек квадрата \(0\leqslant x\leqslant1,\) \(0\leqslant y\leqslant1\) имеет мощность континуума. Таким образом, грубо говоря, в квадрате «столько же» точек, сколько и в отрезке.

Источник

Множества

Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.

Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:

N — множество натуральных чисел,

Z — множество целых чисел.

Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.

Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись

означает, что множество L состоит из четырёх чётных чисел.

Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.

Подмножество

Подмножество — это множество, все элементы которого, являются частью другого множества.

Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.

Рассмотрим два множества:

Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :

Рассмотрим два множества:

Так как оба множества состоят из одних и тех же элементов, то L = M.

Пересечение и объединение множеств

Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.

При объединении равных множеств объединение будет равно любому из данных множеств:

Источник

Понятие множества. Основные определения

Элементы теории множеств

Понятие множества является фундаментальным неопределимым понятием, одно из основных, если не основное, понятий математики. Оно не имеет точного определения, и его следует отнести к аксиоматическим понятиям. Как правило, термин множество объясняется с помощью примеров, а потом указываются правила его использования в математических применениях. Последнее можно сделать на разных уровнях строгости. Детальное и строгое изложение теории множеств требовало бы скрупулезного анализа логики математических рассуждений, а это – специальная самостоятельная тема, которая относится к области основ математики. Для наших целей достаточно выбрать уровень так называемой интуитивной теории множеств.

Интуитивно под множеством понимается совокупность определенных, вполне различимых объектов, рассматриваемых как единое целое. Можно говорить о множестве граней многоугольника, множестве точек на прямой, множестве натуральных чисел, множестве рациональных чисел, множестве операторов языка программирования, множестве языков программирования и т.д. Из этих примеров видно, что множество – это совокупность определенных различаемых объектов таких, что для любого объекта можно установить, принадлежит этот объект данному множеству или нет. Вполне очевидно, что множество, которое подчиняется такому ограничению, может содержать объекты почти любой природы. Например: множество жителей города Сарова; множество студентов СарФТИ; множество автобусных маршрутов нашего города; множество станций московского метро; множество правых ботинок; множество символов кодов компьютера; множество идентификаторов в программе и т.д. Следует подчеркнуть, что о множестве можно вести речь только тогда, когда элементы множества различимы между собой. Например, нельзя говорить о множестве капель в стакане воды, т.к. невозможно четко и ясно указать каждую отдельную каплю.

Множества, все элементы которого являются числами, называются числовыми множествами. Множества, элементами которого являются другие множества, называются классом или семейством.

Отдельные объекты, из которых состоит множество, называют элементами множества. Например, 5 – элемент множества натуральных чисел, G – элемент множества букв латинского алфавита.

Таким образом, когда мы говорим о множестве, то объединяем некоторые объекты в одно целое, а именно в множество, элементами которого они являются.

Основатель теории множеств Георг Кантор определил формулировку интуитивного понятия множества следующими словами: «Произвольная совокупность определенных предметов нашей интуиции или интеллекта, которые можно отличить один от другого и которые представляются как единое целое, называется множеством. Предметы, которые входят в состав множества, называются его элементами».

Существенным пунктом канторовского понятия множества является то, что совокупность предметов рассматривается как один предмет («представляется как единое целое»). Основное внимание тут переносится с отдельных предметов на совокупности предметов, которые в свою очередь, можно рассматривать как предметы.

Что касается «предметов нашей интуиции или интеллекта», то эта формулировка дает значительную свободу прежде всего тем, что никак не ограничивает природу предметов, составляющих множество. Множество может состоять, например, из людей, простых чисел, точек пространства, планет Вселенной и т.д. Заметим, что канторовская формулировка множества дает возможность рассматривать множества, элементы которых по определенной причине точно задать невозможно.

Смысл выражений: «которые можно отличить один от другого» и «определенные предметы» заключается в следующем. В первом случае для любых двух предметов, которые рассматриваются как элементы данного множества, должна существовать возможность выяснить, различные эти предметы или одинаковые. Во втором случае, если задано некоторое множество и какой-нибудь предмет, то можно определить, является ли этот предмет элементом данного множества. Отсюда следует, что всякое множество полностью определяется своими элементами. Это канторовское требование формулируется как интуитивный принцип объемности или аксиома экстенсиональности, согласно которому два множества (А и В) равны тогда и только тогда, когда они состоят из одних и тех же элементов (обозначают А=В).

Таким образом, два множества равны, если каждый элемент одного из них является элементом другого и наоборот.

Общим обозначением множества служит пара фигурных скобок <…>, внутри которых перечисляются элементы множества. Для обозначения конкретных множеств используют различные прописные буквы (М, Х, А,…), или прописные с индексами (М₁, М₂, …). Для обозначения элементов множества в общем случае используют различные строчные буквы, или строчные буквы с индексами. Для указания того, что некоторый элемент a является элементом множества А, используется символ принадлежности множеству Î[1]. Запись аÎА означает, что элемент а принадлежит множеству А, а запись аÏА означает, что элемент а не принадлежит множеству А. Записью а₁, а₂, … а_n ÎА пользуются в качестве сокращения для записи а₁ÎА, а₂ÎА, а₃ÎА, …а_nÎА.

Множества бывают конечными и бесконечными. Множество называют конечным, если число его элементов конечно, т.е. если существует натуральное число N, являющееся числом элементов множества. Множество называют бесконечным, если оно содержит бесконечное число элементов.

1.2 Способы задания множества

Существует два основных способа задания множества: перечисление и описание.

Например, множество отличников группы можно задать, перечислив студентов, которые учатся на “отлично”. Например: <Иванов, Сидоров, Петров,…>.

Для сокращения записи А=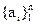1, a₂, … a_n > иногда пишут A= , или вводят множество индексов I= <1,2,….n>и пишут А=i>, iÎI. Такой способ удобен при рассмотрении конечных множеств, содержащих небольшое число элементов.

Описательный способ задания множества состоит в том, что указывается характерное свойство, которым обладают все элементы множества. Под свойством предмета х будем понимать такое повествовательное предложение, в котором нечто утверждается относительно предмета х и которое можно характеризовать как истинное или ложное по отношению к х (характеристический предикат).

Например, свойствами являются:

Пусть N множество целых чисел. Тогда > есть множество <1,2,3,4,5,6,7>.

Важным понятием теории множеств является понятие пустого множества. Пусть А – некоторое множество, а Р(х) имеет вид х ¹ х, тогда множество = , очевидно, не имеет элементов. Из принципа объемности следует, что может существовать только одно множество, которое не имеет элементов. Это множество и называется пустым множеством.

Или, Пустыммножеством называют множество, не содержащее ни одного элемента. Пустое множество обозначается символом Æ.

Пустое множество условно относится к конечным множествам.

Задание множества называют неизбыточным, если каждый элемент входит в данное множество в единственном экземпляре, и избыточным, если хотя бы один элемент входит в его состав более чем в одном экземпляре (мультимножества).

1.3 Равенство множеств

Как уже отмечалось, два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют собой одно и тоже множество. Символ равенства множеств обладает свойствами:

· если А=В, то В=А – симметричность;

· если А=В и В=С, то А=С – транзитивность.

Из определения равенства множеств вытекает:

1. порядок элементов в множестве несуществен. Например, множества <1,2,3,4>и <3,4,1,2>представляют собой одно и тоже множество;

2. в множестве не должно быть неразличимых элементов. Поэтому в множестве не должно быть одинаковых элементов. Например, запись множества А= <6,7,8,6,9>следует рассматривать как А=<6,7,8,9>1.

Но, множество, которое состоит из элементов некоторого множества А так, что эти элементы могут входить в состав этого множества в любом количестве экземпляров, называют мультимножеством множества А. С точки зрения теории множеств, множество и мультимножество – это один и тот же объект и они могут между собой не различаться. Однако часто, особенно когда речь идет о представлении множества в памяти ЭВМ, возникает потребность отличать множество от мультимножества.

1.4 Подмножество

Множество А является подмножеством множества В, если любой элемент множества А принадлежит и множеству В.

Например, множество студентов группы является подмножеством студентов факультета; множество четных целых чисел может рассматриваться как подмножество множества натуральных чисел.

Для определения подмножества в теории множеств используются символы:

· ® (или Þ) символ следствия (импликации), означающий “влечет за собой”; “если… то”;

Тогда определение подмножества, которое может быть сформулировано в виде: для любого х утверждение “х принадлежит А“ влечет за собой утверждение “х принадлежит В” запишется так:

1.1

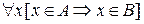
Более краткой записью выражение “A является подмножеством B” будет запись

1.2

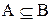
(Читается “В содержит А”).

Используемый здесь символ Í означает включение.

Если множество В содержит и другие элементы кроме элементов из А, то используют символ строгого включения Ì и обозначается это А Ì В. В этом случае А называется собственным подмножеством множества В

Связь между символами дается выражениями:

1.3

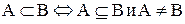
· АÍА – рефлексивность; (AËA – иррефлексивность) 1.4

· [AÍB и BÍC] ® AÍC – транзитивность. 1.5

Следует отметить важное свойство, что для любого множества А пустое множество Æ Í A.

Если АÍВ и ВÍА, то множества А и В эквивалентны: А=В, т.е. все эле-менты А являются элементами В, а все элементы В являются элементами А.

Т.е. А=В Û ( )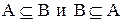

Определение. Множество всех подмножеств данного множества А называют булеаном или степеньюмножества А и обозначают β(А)1.

Формально β(А)=. В частности заметим, что поскольку Æ Í А и А Í А, то Æ Î β(А); А Î β(А).

1.5 Операции над множествами

1.5.1 Предварительные замечания

Над множествами можно производить действия, которые во многом напоминают действия сложения и умножения в элементарной алгебре. Если а и b некоторые числа, то законы элементарной алгебры можно записать как:

2. — ассоциативный (сочетательный) закон;

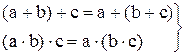
Заметим, что в ассоциативном и коммутативном законах можно заменить действие сложения умножением, а действие умножения – сложением. При этом получим другой закон, который будет справедлив как и первый. Однако в дистрибутивном законе подобной симметрии нет. Если в этом законе заменить сложение умножением, а умножение сложением, то придем к абсурду

.

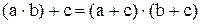
Всегда ли это так? Оказывается существуют алгебры, и именно алгебра множеств, в которой все три закона симметричны относительно действий “сложения” и “умножения”.

1.5.2 Объединение множеств

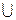
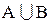
Объединением множеств А и В называют множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А и В. Объединение множеств А и В обозначается символом , т.е. .

Определение объединения множеств можно записать как

1.6

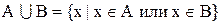
Объединение множеств иногда называют суммой множеств и обозначают А+В. Однако свойства объединения множеств несколько отличаются от свойств суммы при обычном арифметическом понимании. Поэтому термином сумма пользоваться не рекомендуется.

Источник