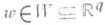Что понимается под позиционным управлением
Позиционном управлении
Программное управление, в свою очередь, подразделяется на два вида: контурное управление и позиционное. Контурным управлением называется программное управление промышленным роботом, при котором движение ^го исполнительного устройства программируется в виде траектории в рабочем пространстве с непрерывным контролем по скорости. Позиционным управлением.называется программное управление промышленным роботом, при котором движение его исполнительного устройства программируется по упорядоченной во времени конечной последовательности точек рабочего пространства без контроля движения между ними. Частным случаем позиционного управления является цикловое управле-
Позиционное управление по многим точкам или контурное управление, рассматриваемое как предельный случай позиционного управления при увеличении числа позиций, применяется для выполнения технологических операций типа сварки и покраски. Для реализации контурного управления необходимо уже использовать программоносители в виде перфоленты или магнитной ленты подобно тому, как они используются в станках с ЧПУ (см. § 29).
Использование этого алгоритма позволяет отказаться от представления в явном виде преобразования декартовых координат захвата в обобщенные координаты манипулятора. При этом точность воспроизведения заданной кривой между узлами интерполирования определяется степенью интерполяционного многочлена. По сравнению с контурным (непрерывным) управлением применение интерполяционных многочленов в условиях позиционного управления позволяет уменьшать необходимый объем памяти, обеспечивая одновременно необходимую точность воспроизведения заданной кривой.
Обычно применяемый при регулировании отрицательных температур способ позиционного управления [22] характеризуется повышенным расходом азота и недостаточной надежностью контактных устройств.
Непрерывные (контурные) системы программного управления предназначены для обработки деталей сложного контура, описанного, наряду с прямыми, криволинейными отрезками различной кривизны и направленности. Сюда могут быть отнесены полости штампов и пресс-форм, лопатки турбин, различного рода кулачки, кронштейны и т. д. Управление положением рабочего органа в этом случае ведется непрерывно. Если в системах позиционного управления отсутствовала функциональная зависимость между перемещениями по отдельным координатам, а сами перемещения, за исключением систем прямоугольного управления, не являлись рабочими и осуществлялись на максимальных скоростях, то для систем контурного управления характерно как раз наличие такой функциональной зависимости, причем при объемной обработке — по трем координатам.
Некоторые особенности систем позиционного управления
Рис. 133. Цикл перемещения шпинделя по оси Z в станках позиционного управления (при обычном сверлении или растачивании, при отсутствии воздушных промежутков):
Обычно начало координат детали совмещается с началом системы координат станка или привязывается к нему, поскольку отсчет перемещений ведется от начала системы координат станка. Однако на вертикально-фрезерных станках с импульсными системами управления отсчет координат ведется не от указанной точки, а от предыдущего положения. На рис. 147 цифрой 1 отмечено исходное положение, в которое выводится шпиндель в начале обработки. Отрезок /—2 соответствует быстрому подводу фрезы, 2—3 — врезанию, 3—4 и последующие участки—рабочим перемещениям. Каждая обрабатываемая поверхность на чертеже задается базовыми и опорными точками, координаты которых в системе координат детали должны быть рассчитаны (это не относится к обработке деталей на станках позиционного управления: координаты обрабатываемых отверстий имеются в этом случае на чертеже и нет необходимости проставлять для них дополнительные опорные точки).
Некоторые особенности систем позиционного управления. 209
При позиционном управлении задают независимые перемещения по каждой координате, соответствующие требуемой точке рабочей зоны манипулятора.
При позиционном управлении задают независимые перемещения по каждой координате, соответствующие требуемой точке рабочей зоны манипулятора.
Виды управления. По способу задания движения захвата различают контурное (непрерывное) управление и позиционное управление. При контурном управлении задается непрерывное движение некоторой точки захвата по требуемой траектории, а при позиционном управлении задаются только отдельные положения захвата.
При позиционном управлении основной целью введения обратных связей является уменьшение ошибки позиционирования, под которой обычно понимается какая-либо мера, определяющая «расстояние» между действительным и программным положениями системы.
ности программного изменения скорости нагружения по каждому каналу. Управление подачей масла в цилиндры и сливом производится с помощью включения и выключения электрогидравлических кранов, причем, как правило, переключение кранов производится в экстремальных точках программы нагружения. В этих условиях скорости нарастания нагрузок в основном определяются характеристиками жесткости конструкции и расходными характеристиками трубопроводов и кранов. Поэтому при позиционном управлении можно воспроизводить весьма ограниченное число комбинаций нагрузок.
Числовое программное управление станком (ЧПУ) — управление обработкой заготовки на станке по управляющей программе, в которой данные заданы в цифровой форме. Различают позиционное и контурное ЧПУ. При позиционном управлении перемещение рабочих органов станка происходит в заданные точки, причем траектория перемещения не задается; при контурном управлении перемещение рабочих органов станка происхо-
Наличие микроЭВМ в системе АПУ позволяет необычайно расширить ее функциональные возможности. Например, можно оптимизировать последовательность обхода позиций сверления (при позиционном управлении), интерполировать траектории фрезерования (при контурном управлении), компенсировать люфты в редукторах посредством вычисления необходимых программных коррекций и т. п.
Рис. 5.3. Переходные процессы при адаптивном позиционном управлении: а — процессы позиционирования; б — процессы адаптации
Команды движения при позиционном управлении перемещениями от точки к точке определяется последовательностью положений вершины инструмента в абсолютной или относительной системе координат. Абсолютное перемещение задается фразой
В системах с абсолютным отсчетом все размеры задаются и отсчитываются от одной (не изменяемой в процессе отработки) &13Ы. Эти системы свободны от «накопленной» ошибки. Этот Принцип используется при позиционном управлении.
ности программного изменения скорости нагружения по каждому каналу. Управление подачей масла в цилиндры и сливом производится с помощью включения и выключения электрогидравлических кранов, причем, как правило, переключение кранов производится в экстремальных точках программы нагружения. В этих условиях скорости нарастания нагрузок в основном определяются характеристиками жесткости конструкции и расходными характеристиками трубопроводов и кранов. Поэтому при позиционном управлении можно воспроизводить весьма ограниченное число комбинаций нагрузок.
Математическая энциклопедия
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПОЗИЦИОННОЕ
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПОЗИЦИОННОЕ
Простейшая задача синтеза, напр. для системы
и. заданным «терминальным» показателем
на минимум того же функционала 
и при тех же самых ограничениях. Далее полагается, что
и если функция u 0 (t, x).корректно определена, а уравнение
имеет единственное решение, то задача синтеза решена, причем оптимальные значения показателя I, найденные в классах программных и позиционных управлений, совпадают (в общем случае выделяют условия, обеспечивающие существование в определенном содержательном смысле решений уравнения (3), и условия, гарантирующие оптимальность всех траекторий этого уравнения).
Нахождение u 0 (t, x).сразу в виде функции текущего состояния связано с использованием метода динамического программирования (см. [2]). Вводимая в рассмотрение функция действия (функция Б е л л м а н a) V(t, х), имеющая смысл минимума (максимума) оптимизируемой величины (напр., функционала
Вывод уравнения (5) для задачи синтеза опирается на принцип оптимальности, утверждающий, что отрезок оптимальной траектории есть снова оптимальная траектория (см. [2]). Правомерность такого подхода зависит от корректного определения информационных свойств процесса и, в частности, понятия позиции (текущего состояния, см. [5]).
тогда означает, что u 0 (t, х) = и 0 (х).осуществляет спуск оптимальной траектории х 0 (t).относительно поверхностей уровня функции V(х).наискорейшим из способов, допускаемых условием 
Применение метода динамич. программирования (как достаточного условия оптимальности) будет обосновано, если функция V(t, x).всюду удовлетворяет определенным условиям гладкости (напр., в задаче (3)-(6) функция V(t, х).должна быть непрерывно дифференцируемой) или если условия гладкости выполняются всюду, за исключением нек-рого «особого» множества N. При выполнении нек-рых специальных «условий регулярного синтеза» метод динамич. программирования оказывается эквивалентным принципу Понтрягина, к-рый тогда выступает как необходимое и достаточное условие оптимальности (см. [8]). Трудности, связанные с априорной проверкой применимости метода динамич. программирования и с необходимостью решать дифференциальное уравнение Беллмана с частными производными, усложняют использование этого метода. Метод динамического программирования нашел распространение в задачах синтеза оптимального управления для дискретных (многошаговых) систем, где соответствующее уравнение Беллмана конечно-разностное (см. [2], [9]).
Свойство полной наблюдаемости, как и построение соответствующих аналитич. операций, выделяющих х(J), а также оптимизация этих операций хорошо изучены для линейных систем. Здесь известен принцип дуальности, состоящий в том, что каждой задаче наблюдения может быть поставлена в соответствие эквивалентная двухточечная краевая задача управления для дуальной системы. Вследствие этого оказывается, что свойство полной наблюдаемости линейной системы совпадает со свойством полной управляемости дуальной системы с управлением. Более того, оказывается, что и соответствующие дуальные экстремальные задачи об оптимальном наблюдении и оптимальном управлении могут быть составлены так, что их решения совпадут (см. [3]). Свойства управляемости и наблюдаемости линейных систем допускают весьма разнообразные обобщения на линейные бесконечномерные объекты (уравнения в банаховом пространстве, системы с отклоняющимся аргументом, дифференциальные уравнения с частными производными). Имеется и ряд результатов, характеризующих соответствующие свойства. Для нелинейных систем известен лишь ряд локальных теорем о наблюдаемости. Решения проблемы наблюдения нашли многочисленные применения в задачах синтеза в условиях неполной информации о координатах, в том числе в задачах оптимальной стабилизации (см. [3]-[5], [14], [15]).
Задача синтеза становится особенно содержательной, когда информация об уравнениях управляемого процесса, исходных начальных условиях и текущих параметрах искажена возмущениями. Если описание возмущений носит статистич. характер, то задачи оптимального управления рассматривают в рамках теории стохастического оптимального управления. Эта теория, начатая с решения стохастических программных задач [10], в наибольшей степени разработана для систем вида
со случайными возмущениями h(t), описываемыми гауссовскими диффузионными процессами или более общими классами марковских процессов (начальный вектор обычно также считают случайным). При этом, как правило, предполагается, что заданы нек-рые вероятностные характеристики величин h(напр., сведения о моментах соответствующих распределений или о параметрах стохастич, уравнений, описывающих эволюцию процесса h(t)).
В общем случае применение программных и синтезирующих управлений здесь дает существенно различные значения оптимальных показателей J качества (роль таких показателей могут играть, напр., те или иные средние оценки неотрицательных функционалов, заданных на траекториях процесса). Задача синтеза стохастического оптимального управления теперь имеет очевидные преимущества, т. к. непрерывное измерение координат системы позволяет корректировать движение с учетом реального хода случайного процесса, непредсказуемого заранее. Здесь было обнаружено, что метод динамич. программирования совершенно естественным образом сопрягается с теорией бесконечно малых производящих операторов для полугрупп преобразований, генерируемый марковскими случайными процессами. Эти обстоятельства позволили построить и строго обосновать серию достаточных условий оптимальности, приведших к решению на конечном и бесконечном интервале времени ряда задач о синтезе стохастического оптимального управления с полной и неполной информацией о текущих координатах, стохастич. задач преследования и т. д. При этом существенно, что для справедливости принципа оптимальности управление и здесь должно строиться в каждый момент времени t как функция «достаточных координат» z процесса, для к-рых будет обеспечено свойство марковости (см. [5], [6], [17], [18]).
Таким путем, в частности, была разработана теория оптимальной стохастической стабилизации, связанная с соответствующей теорией устойчивости по Ляпунову, развитой для сто-хастич. систем [19].
Для формирования синтезирующего оптимального управления, а также для иных целей управления целесообразно оценивать состояние стохастич. системы по результатам измерения. Решению этого вопроса при условии, что процесс измерения искажается вероятностными «шумами» (т. е. решению задачи наблюдения в условиях случайных возмущений), посвящена теория стохастической фильтрации. Наиболее полные решения здесь известны для линейных систем с квадратичными критериями оптимума (т. н. фильтр Калмана-Бьюси, см. [13]). В применении этой теории к задаче синтеза стохастического оптимального управления были выявлены условия, обеспечивающие справедливость принципа разделения, позволяющего решать собственно задачу управления независимо от задачи оценивания текущих позиции на основе достаточных координат процесса (см. [20]; более общим закономерностям стохастич. фильтрации, а также задачам стохастич. оптимального управления, когда само управление выбирается в классе марковских процессов диффузионного типа, посвящены работы [18], |21]).
Строго формализованное решение задачи стохастического оптимального управления неизбежно соприкасается с проблемой корректного обоснования вопросов существования решений соответствующих стохастических дифференциальных уравнений. Последнее обстоятельство порождает определенные трудности в решении задач стохастического оптимального управления при наличии неклассич. ограничении.
Содержательный процесс динамич. оптимизации возникает в задачах синтеза оптимального управления в условиях неопределенности (см. Оптимальное управление программное). Позиционные решения в общем случае позволяют и здесь улучшить показатели качества процесса по сравнению с программными, представляющими собой все-таки результат статич. оптимизации (проводимой, правда, в пространстве динамич. систем и функций-управлений). К решению задач тогда привлекают понятия и методы теории игр.
Пусть имеется система
(8) при ограничениях
Наиболее полные решения здесь известны для линейных систем и выпуклых ограничений (см. [22]).
В общем случае выбор позиционной стратегии оптимального управления в условиях неопределенности (напр., в виде функционала 
) должен быть нацелен на управление эволюцией областей 
(т. е. на изменение их конфигурации и перемещение их в пространстве) в соответствии с предписанными критериями. Для указанной задачи известен ряд общих качественных результатов, а также конструктивных решений в классе специальных линейно-выпуклых задач (см. [7], [22]). При этом информация, доставляемая измерениями (напр., функцией y[t] в системе (8), (9)), позволяет по ходу процесса апостериорным образом переоценивать области допустимых значений неопределенных параметров в направлении их сужения. Таким образом попутно решается задача идентификации математич. модели процесса (напр., параметров wуравнения (8)). Сказанное позволяет трактовать решения задачи о синтезе оптимального управления в условиях неопределенности как процедуру адаптивного оптимального управления, в к-ром уточнение свойств модели процесса переплетается с выбором управляющего воздействия как такового. Вопросы идентификации моделей динамич. процессов и задачи адаптивного оптимального управления подробно изучены в предположениях о существовании того или иного вероятностного описания неопределенных параметров (см. [23], [24]).
Если в задачах синтеза оптимального управления в условиях неопределенности трактовать параметры w,E как «управления» фиктивного игрока-противника, то цели управлений ии
Лит.:[1] Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф., Математическая теория оптимальных процессов, 3 изд., М., 1970; [2] Беллман Р., Динамическое программирование, пер. с англ., М., 1960; [3] Красовский Н. Н., Теория управления движением, М., 1968; [4] его же, «Дифференциальные уравнения», 1965, т. 1, №1, с. 5-16; [5] его же, в сб.: Механика в СССР за 50 лет, т. 1, М., 1968, с. 179-244; [6] его же, «Прикл. матем. и мех.», 1961, т. 25, № 5, с. 806-17; [7] Красовский Н. Н., Субботин А. И., Позиционные дифференциальные игры, М., 1974; [8] Болтянский В. Г., Математические методы оптимального управления, М., 1966; [9] его же, Оптимальное управление дискретными системами, М., 1973; [10] Летов А. М., Математическая теория процессов управления, М., 1981; [11] Лионc Ж., Оптимальное управление системами, описываемыми уравнениями с частными производными, пер. с франц., М., 1972; [12] Калман Р., в кн.: Труды 1 Международного конгресса Международной федерации по автоматическому управлению, т. 2, М., 1961, с. 521-47; [13] Калман Р., Бьюси Р., «Труды Амер. об-ва инженеров-механиков. Сер. 1, Д.», 1961, т. 83, с. 123; [14] Л и 3.-Б., Mapкус Л., Основы теории оптимального управления, пер. с англ., М., 1972; [15] Бутковский А. Г., Структурная теория распределенных систем, М., 1977; [16] Колмогоров А. Н., Мищенко Е. Ф., Понтрягин Л. С., «Докл. АН СССР», 1962, т. 145, № 5, с. 993-95; [17] Лиццер Р. Ш., Щиряев А. Н., Статистика случайных процессов, М., 1974; [18] Острем К. Ю., Введение в стохастическую теорию управления, пер. с англ, М., 1973; [19] Кац И. Я., Красовский Н. Н., «Прикл. матем. и мех.», 1960, т. 24, № 5, с. 809-23; [20] Wonham W. M., «SIAM J. Contr.», 1968, v. 6, p. 312-26; [21] Крылов Н. В., Управляемые процессы диффузионного типа, М., 1977; [22] КуржанскийА. <Б., Управление и наблюдение в условиях неопределенности, М., 1977; [23] Цыпкин Я. 3., Основы теории обучающихся систем, М., 1970; [24] Эйкхофф П., Основы идентификации систем управления, пер. с англ., М., 1975.
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПОЗИЦИОННОЕ
Простейшая задача синтеза, напр. для системы
и. заданным «терминальным» показателем
на минимум того же функционала 
и при тех же самых ограничениях. Далее полагается, что
имеет единственное решение, то задача синтеза решена, причем оптимальные значения показателя I, найденные в классах программных и позиционных управлений, совпадают (в общем случае выделяют условия, обеспечивающие существование в определенном содержательном смысле решений уравнения (3), и условия, гарантирующие оптимальность всех траекторий этого уравнения).
Нахождение u 0 (t, x).сразу в виде функции текущего состояния связано с использованием метода динамического программирования (см. [2]). Вводимая в рассмотрение функция действия (функция Б е л л м а н a) V(t, х), имеющая смысл минимума (максимума) оптимизируемой величины (напр., функционала
(4)
для системы (1) при x(t)=x:, 
, должна удовлетворять дифференциальному уравнению Беллмана с частными производными и с краевыми условиями, зависящими от цели управления и показателя J. Для системы (1), (2), (4) это уравнение имеет вид
(5) где
(6)
Вывод уравнения (5) для задачи синтеза опирается на принцип оптимальности, утверждающий, что отрезок оптимальной траектории есть снова оптимальная траектория (см. [2]). Правомерность такого подхода зависит от корректного определения информационных свойств процесса и, в частности, понятия позиции (текущего состояния, см. [5]).
тогда означает, что u 0 (t, х) = и 0 (х).осуществляет спуск оптимальной траектории х 0 (t).относительно поверхностей уровня функции V(х).наискорейшим из способов, допускаемых условием 
Применение метода динамич. программирования (как достаточного условия оптимальности) будет обосновано, если функция V(t, x).всюду удовлетворяет определенным условиям гладкости (напр., в задаче (3)-(6) функция V(t, х).должна быть непрерывно дифференцируемой) или если условия гладкости выполняются всюду, за исключением нек-рого «особого» множества N. При выполнении нек-рых специальных «условий регулярного синтеза» метод динамич. программирования оказывается эквивалентным принципу Понтрягина, к-рый тогда выступает как необходимое и достаточное условие оптимальности (см. [8]). Трудности, связанные с априорной проверкой применимости метода динамич. программирования и с необходимостью решать дифференциальное уравнение Беллмана с частными производными, усложняют использование этого метода. Метод динамического программирования нашел распространение в задачах синтеза оптимального управления для дискретных (многошаговых) систем, где соответствующее уравнение Беллмана конечно-разностное (см. [2], [9]).
В прикладных задачах синтеза оптимального управления измерение всех фазовых координат системы доступно далеко не всегда. Поэтому возникает следующая задача наблюдения, допускающая многочисленные обобщения: зная на промежутке 
реализацию 
доступной измерению функции y=g(t, х).координат системы (1) (при известном u(t), напр. при 
, и 
), найти вектор 
в заданный момент J. Системы, позволяющие по реализации y[t]однозначным образом восстанавливать 
, каким бы он ни был, наз. вполне наблюдаемыми.
Свойство полной наблюдаемости, как и построение соответствующих аналитич. операций, выделяющих х(J), а также оптимизация этих операций хорошо изучены для линейных систем. Здесь известен принцип дуальности, состоящий в том, что каждой задаче наблюдения может быть поставлена в соответствие эквивалентная двухточечная краевая задача управления для дуальной системы. Вследствие этого оказывается, что свойство полной наблюдаемости линейной системы совпадает со свойством полной управляемости дуальной системы с управлением. Более того, оказывается, что и соответствующие дуальные экстремальные задачи об оптимальном наблюдении и оптимальном управлении могут быть составлены так, что их решения совпадут (см. [3]). Свойства управляемости и наблюдаемости линейных систем допускают весьма разнообразные обобщения на линейные бесконечномерные объекты (уравнения в банаховом пространстве, системы с отклоняющимся аргументом, дифференциальные уравнения с частными производными). Имеется и ряд результатов, характеризующих соответствующие свойства. Для нелинейных систем известен лишь ряд локальных теорем о наблюдаемости. Решения проблемы наблюдения нашли многочисленные применения в задачах синтеза в условиях неполной информации о координатах, в том числе в задачах оптимальной стабилизации (см. [3]-[5], [14], [15]).
Задача синтеза становится особенно содержательной, когда информация об уравнениях управляемого процесса, исходных начальных условиях и текущих параметрах искажена возмущениями. Если описание возмущений носит статистич. характер, то задачи оптимального управления рассматривают в рамках теории стохастического оптимального управления. Эта теория, начатая с решения стохастических программных задач [10], в наибольшей степени разработана для систем вида
(7)
со случайными возмущениями h(t), описываемыми гауссовскими диффузионными процессами или более общими классами марковских процессов (начальный вектор обычно также считают случайным). При этом, как правило, предполагается, что заданы нек-рые вероятностные характеристики величин h(напр., сведения о моментах соответствующих распределений или о параметрах стохастич, уравнений, описывающих эволюцию процесса h(t)).
В общем случае применение программных и синтезирующих управлений здесь дает существенно различные значения оптимальных показателей J качества (роль таких показателей могут играть, напр., те или иные средние оценки неотрицательных функционалов, заданных на траекториях процесса). Задача синтеза стохастического оптимального управления теперь имеет очевидные преимущества, т. к. непрерывное измерение координат системы позволяет корректировать движение с учетом реального хода случайного процесса, непредсказуемого заранее. Здесь было обнаружено, что метод динамич. программирования совершенно естественным образом сопрягается с теорией бесконечно малых производящих операторов для полугрупп преобразований, генерируемый марковскими случайными процессами. Эти обстоятельства позволили построить и строго обосновать серию достаточных условий оптимальности, приведших к решению на конечном и бесконечном интервале времени ряда задач о синтезе стохастического оптимального управления с полной и неполной информацией о текущих координатах, стохастич. задач преследования и т. д. При этом существенно, что для справедливости принципа оптимальности управление и здесь должно строиться в каждый момент времени t как функция «достаточных координат» z процесса, для к-рых будет обеспечено свойство марковости (см. [5], [6], [17], [18]).
Таким путем, в частности, была разработана теория оптимальной стохастической стабилизации, связанная с соответствующей теорией устойчивости по Ляпунову, развитой для сто-хастич. систем [19].
Для формирования синтезирующего оптимального управления, а также для иных целей управления целесообразно оценивать состояние стохастич. системы по результатам измерения. Решению этого вопроса при условии, что процесс измерения искажается вероятностными «шумами» (т. е. решению задачи наблюдения в условиях случайных возмущений), посвящена теория стохастической фильтрации. Наиболее полные решения здесь известны для линейных систем с квадратичными критериями оптимума (т. н. фильтр Калмана-Бьюси, см. [13]). В применении этой теории к задаче синтеза стохастического оптимального управления были выявлены условия, обеспечивающие справедливость принципа разделения, позволяющего решать собственно задачу управления независимо от задачи оценивания текущих позиции на основе достаточных координат процесса (см. [20]; более общим закономерностям стохастич. фильтрации, а также задачам стохастич. оптимального управления, когда само управление выбирается в классе марковских процессов диффузионного типа, посвящены работы [18], |21]).
Строго формализованное решение задачи стохастического оптимального управления неизбежно соприкасается с проблемой корректного обоснования вопросов существования решений соответствующих стохастических дифференциальных уравнений. Последнее обстоятельство порождает определенные трудности в решении задач стохастического оптимального управления при наличии неклассич. ограничении.
Содержательный процесс динамич. оптимизации возникает в задачах синтеза оптимального управления в условиях неопределенности (см. Оптимальное управление программное). Позиционные решения в общем случае позволяют и здесь улучшить показатели качества процесса по сравнению с программными, представляющими собой все-таки результат статич. оптимизации (проводимой, правда, в пространстве динамич. систем и функций-управлений). К решению задач тогда привлекают понятия и методы теории игр.
Пусть имеется система
(8) при ограничениях
(9)
где неопределенные параметры x стеснены известным априорным ограничением 
. Знание y[t], 
(при заданном u(t)), позволяет построить и фазовом пространстве информационную область 
) состояний системы (8), совместимых с реализацией у[t], уравнением (9) и ограничениями на w, x. Среди элементов 
будет содержаться и неизвестное истинное состояние системы (8), к-рое может быть оценено выбором нек-рой точки 
из 
(напр., «центра тяжести» или «чебышевского центра» 
). Изучение эволюции областей 
и динамики векторов 
составляет содержание теории минимаксной фильтрации.
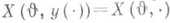
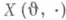
Наиболее полные решения здесь известны для линейных систем и выпуклых ограничений (см. [22]).
В общем случае выбор позиционной стратегии оптимального управления в условиях неопределенности (напр., в виде функционала 
) должен быть нацелен на управление эволюцией областей 
(т. е. на изменение их конфигурации и перемещение их в пространстве) в соответствии с предписанными критериями. Для указанной задачи известен ряд общих качественных результатов, а также конструктивных решений в классе специальных линейно-выпуклых задач (см. [7], [22]). При этом информация, доставляемая измерениями (напр., функцией y[t] в системе (8), (9)), позволяет по ходу процесса апостериорным образом переоценивать области допустимых значений неопределенных параметров в направлении их сужения. Таким образом попутно решается задача идентификации математич. модели процесса (напр., параметров wуравнения (8)). Сказанное позволяет трактовать решения задачи о синтезе оптимального управления в условиях неопределенности как процедуру адаптивного оптимального управления, в к-ром уточнение свойств модели процесса переплетается с выбором управляющего воздействия как такового. Вопросы идентификации моделей динамич. процессов и задачи адаптивного оптимального управления подробно изучены в предположениях о существовании того или иного вероятностного описания неопределенных параметров (см. [23], [24]).
Если в задачах синтеза оптимального управления в условиях неопределенности трактовать параметры w,E как «управления» фиктивного игрока-противника, то цели управлений ии
Лит.:[1] Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф., Математическая теория оптимальных процессов, 3 изд., М., 1970; [2] Беллман Р., Динамическое программирование, пер. с англ., М., 1960; [3] Красовский Н. Н., Теория управления движением, М., 1968; [4] его же, «Дифференциальные уравнения», 1965, т. 1, №1, с. 5-16; [5] его же, в сб.: Механика в СССР за 50 лет, т. 1, М., 1968, с. 179-244; [6] его же, «Прикл. матем. и мех.», 1961, т. 25, № 5, с. 806-17; [7] Красовский Н. Н., Субботин А. И., Позиционные дифференциальные игры, М., 1974; [8] Болтянский В. Г., Математические методы оптимального управления, М., 1966; [9] его же, Оптимальное управление дискретными системами, М., 1973; [10] Летов А. М., Математическая теория процессов управления, М., 1981; [11] Лионc Ж., Оптимальное управление системами, описываемыми уравнениями с частными производными, пер. с франц., М., 1972; [12] Калман Р., в кн.: Труды 1 Международного конгресса Международной федерации по автоматическому управлению, т. 2, М., 1961, с. 521-47; [13] Калман Р., Бьюси Р., «Труды Амер. об-ва инженеров-механиков. Сер. 1, Д.», 1961, т. 83, с. 123; [14] Л и 3.-Б., Mapкус Л., Основы теории оптимального управления, пер. с англ., М., 1972; [15] Бутковский А. Г., Структурная теория распределенных систем, М., 1977; [16] Колмогоров А. Н., Мищенко Е. Ф., Понтрягин Л. С., «Докл. АН СССР», 1962, т. 145, № 5, с. 993-95; [17] Лиццер Р. Ш., Щиряев А. Н., Статистика случайных процессов, М., 1974; [18] Острем К. Ю., Введение в стохастическую теорию управления, пер. с англ, М., 1973; [19] Кац И. Я., Красовский Н. Н., «Прикл. матем. и мех.», 1960, т. 24, № 5, с. 809-23; [20] Wonham W. M., «SIAM J. Contr.», 1968, v. 6, p. 312-26; [21] Крылов Н. В., Управляемые процессы диффузионного типа, М., 1977; [22] КуржанскийА.