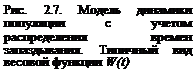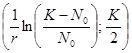Что понимается под продолжительностью жизни вида

Что такое «продолжительность жизни» и что отражают кривые выживания?

Продолжительность жизни ви­да зависит от условий (факто­ров) жизни. Различают физио­логическую и максимальную продолжительность жизни.

Физиологическая продолжительность жизни— это та­кая продолжительность жизни, которая определяется толь­ко физиологическими возможностями организма. Теорети­чески она возможна, если допустить, что в период всей жиз­ни организма на него не оказывают влияние лимитирующие факторы.

Максимальная продолжительность жизни— это такая продолжительность жизни, до которой может дожить лишь малая доля особей в реальных условиях среды. Эта величи­на варьирует в широких пределах: от нескольких минут у бактерий, до нескольких тысячелетий у древесных растений (секвойя). Обычно, чем крупнее растение или животное, тем больше их продолжительность жизни.

Таблицы выживания, или еще их называют демогра­фическими таблицами, содержат сведения о характере рас­пределения смертности по возрастам и используются для определения ожидаемой продолжительности жизни чело­века. Таблицы выживания бывают динамические и стати­ческие.

Динамические таблицыстроятся по данным прямых наблюдений за жизнью когорты, т.е. большой группы осо­бей, отрожденных в популяции за короткий промежуток времени, и регистрации возраста наступления смерти всех членов этой когорты. Такие таблицы требуют длительно­го наблюдения, измеряемого месяцами или годами. По­этому используют другие таблицы — статические.

Статические таблицы выживания составляются по данным наблюдений за смертностью за относительно ко­роткий промежуток времени в отдельных возрастных груп­пах. Зная численность этих групп (сосуществующих ко­горт), можно рассчитать смертность, специфическую для каждого возраста.

Данные таблиц выживания позволяют построить кривые выживания. Выделяют три основных типа кривых выжива­ния (рис. 1). Кривая I типа, когда на протяжении всей жизни смертность мала, резко возрастая в конце нее, харак­терна для насекомых, которые обычно гибнут после кладки яиц (ее и называют «кривой дрозофилы»), к ней приближают­ся кривые выживания человека в развитых странах и некото­рых крупных млекопитающих.

Кривая III типа — случаи массовой гибели особей в на­чальный период жизни. Гидробионты и некоторые другие организмы, не заботящиеся о потомстве, выживают за счет огромного числа личинок, икринок, семян и т.п. Моллюски: до закрепления на дне проходят личиночную стадию в планк­тоне, где личинки гибнут в огромных количествах, поэтому кривую III называют еще «кривой устрицы».

Рис. 1. Различные типы кривых выживания

Кривая II типа(диагональная) характерна для видов, у которых смертность остается примерно постоянной в тече­ние всей жизни. Она характерна для рыб, пресмыкающихся, птиц, многолетних травянистых растений.

Кривые выживания часто представляют собой комбина­цию указанных выше «основных типов». Например, у людей, живущих в отсталых странах, кривая I вначале круто падает за счет повышенной смертности сразу после рождения.

Источник

Видовая продолжительность жизни

Споры относительно видовой продолжительности жизни человека ведутся уже давно. Сравнивая видовую продолжительность жизни различных животных с периодами их роста, учёные пытались вывести общий коэффициент для расчёта продолжительности жизни всех животных, заодно и для человека. Так, в лошадь растёт до 4 лет, а живёт при хорошем уходе до 25–30 лет, рогатый скот растёт в течение 5 лет, а живёт до 35–40 лет. Путём деления срока жизни на срок роста получали искомый коэффициент – 6–7. Этот коэффициент, предложенный свыше 200 лет назад французским естествоиспытателем Жоржем Луи Бюффоном (1707–1783), известен под названием коэффициента Бюффона. Принимая за среднюю продолжительность роста человека 14 лет, Бюффон утверждал, что продолжительность жизни человека должна равняться 90–100 годам.

Кроме коэффициента Бюффона, в разные времена предлагались коэффициенты для расчёта биологической продолжительности жизни животных по среднему сроку внутриутробного развития, по среднему сроку завершения оссификации (окостенения) скелета, по срокам наступления половой зрелости и так далее. Все эти коэффициенты, ориентированные на тенденции и закономерности, существующие в животном мире, определяют человеку от 80 до 200 лет. Чаще всего учёные называют цифру 100 лет, однако, эта цифра не отражает реальной картины. Так, в 70-е годы Б. Ц.Урланис, взяв в качестве основного ориентира продолжительность жизни в наиболее передовых и благополучных странах, путём сложных расчётов и построения кривых пришёл к выводу, что видовая продолжительность жизни человека составляет 86 лет для мужчин и 88 лет для женщин. При этом автор подчёркивал приблизительный характер этих цифр.

Почему же расчёты, в какой-то мере верные для животных, оказываются нереальными для человека? Ответ, видимо, кроется в социо-биологической природе человека. Разграничивая роль биологических и социальных факторов в жизни человека и подчёркивая ведущую роль последних, И. И.Мечников говорил: «Естественный отбор, дойдя до человека, преломляется как луч в призме. Это уже не он больше». По всей видимости, влияние социальных факторов обеспечивает несоответствие онтогенеза человека закономерностям, наблюдающимся в животном мире.

Полезное

Смотреть что такое «Видовая продолжительность жизни» в других словарях:

Продолжительность жизни — Продолжительность жизни: Видовая продолжительность жизни Максимальная продолжительность жизни термин применяется в тех случаях, когда говорят о растениях и животных. Ожидаемая продолжительность жизни термин применяется в тех случаях, когда речь… … Википедия

Продолжительность жизни (значения) — Продолжительность жизни: Видовая продолжительность жизни Максимальная продолжительность жизни термин применяется в тех случаях, когда говорят о растениях и животных. Ожидаемая продолжительность жизни термин применяется в тех случаях, когда речь… … Википедия

ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ ВИДОВАЯ — средний максимальный возраст, достигаемый особями данного вида при наиболее благоприятных условиях среды, т. е. лимитируемый лишь генетическими особенностями особей. См. также Коэффициент Бюффона. Экологический энциклопедический словарь. Кишинев … Экологический словарь

Продолжительность жизни — растений и животных, длительность существования особи (её Онтогенеза), а иногда также Клона. Различают физиологическую, экологическую и среднюю П. ж. Физиологическая П. ж. максимальная для особей данного вида при оптимальных условиях… … Большая советская энциклопедия

Продолжительность жизни человека — показатель определяемый не только биологическими и наследственными особенностями, но и социальными условиями. Человек живет дольше, чем большинство высших позвоночных. Известно, что отдельные индивидуумы доживают до 110 и более лет. Такие рекорды … Физическая Антропология. Иллюстрированный толковый словарь.

Максимальная продолжительность жизни — Максимальная продолжительность жизни согласно классическому определению, максимальная возможная продолжительность жизни представителей определённой группы организмов. В связи со сложностью определения, на практике, это максимальная… … Википедия

Ста́рость. Старе́ние — Старость, старение. Старость закономерно наступающий период возрастного развития, заключительный этап онтогенеза. Старение неизбежный биологический разрушительный процесс, приводящий к постепенному снижению адаптационных возможностей организма;… … Медицинская энциклопедия

Долголетие — Долголетие продолжительность жизни выше среднего срока жизни живого существа (растение, животное, человек). Обычно долголетие достигается при здоровом образе жизни и благоприятных условиях окружающей среды. Долголетие для широкой публики… … Википедия

Российская Советская Федеративная Социалистическая Республика — РСФСР. I. Общие сведения РСФСР образована 25 октября (7 ноября) 1917. Граничит на С. З. с Норвегией и Финляндией, на З. с Польшей, на Ю. В. с Китаем, МНР и КНДР, а также с союзными республиками, входящими в состав СССР: на З. с… … Большая советская энциклопедия

Источник

Сформулируйте экологические законы Б. Коммонера.

Самостоятельная работа по контрольным вопросам

по дисциплине «Системы охотничьих ресурсов »

Ф.И.О. Камелина Екатерина Дмитриевна

Специальность:35.02.14 Охотоведение и звероводство

Форма обучения: очная

1. Что понимается под продолжительностью жизни вида?

2. Сформулируйте экологические законы Б. Коммонера.

3. «Среда обитания» и «Охотничьи угодья». Дайте определения этих понятий в охотоведении и в современной законодательной трактовке.

Что понимается под продолжительностью жизни вида?

Продолжительность жизни вида зависит от условий (факторов) жизни. Различают физиологическую и максимальную продолжительность жизни.

Физиологическая продолжительность жизни¾ это такая продолжительность жизни, которая определяется только физиологическими возможностями организма. Теоретически она возможна, если допустить, что в период всей жизни организма на него не оказывают влияние лимитирующие факторы.

Максимальная продолжительность жизни ¾ это такая продолжительность жизни, до которой может дожить лишь малая доля особей в реальных условиях среды. Эта величина варьирует в широких пределах: от нескольких минут у бактерий до нескольких тысячелетий у древесных растений (секвойя). Обычно, чем крупнее растение или животное, тем больше их продолжительность жизни, хотя бывают и исключения (летучие мыши доживают до 30 лет, это дольше, например, жизни медведя).

Таблицы выживания, или еще их называют «демографическими таблицами», содержат сведения о характере распределения смертности по возрастам. Демография изучает размещение, численность, состав и динамику народонаселения, а эти таблицы она использует для определения ожидаемой продолжительности жизни человека. Таблицы выживания бывают динамические и статические.

Динамические таблицы выживания строятся по данным прямых наблюдений за жизнью когорты, т. е. большой группы особей, отрожденных в популяции за короткий промежуток времени относительно общей продолжительности жизни изучаемых организмов, и регистрации возраста наступления смерти всех членов данной когорты. Такие таблицы требуют длительного наблюдения, измеряемого (для разных животных) месяцами или годами. Но практически невозможно такую таблицу сделать для долго живущих животных, для человека ¾ для этого может потребоваться более 100 лет. Поэтому используют другие таблицы ¾ статические.

Статические таблицы выживания составляются по данным наблюдений за относительно короткий промежуток времени за смертностью в отдельных возрастных группах. Зная численность этих групп (сосуществующих когорт), можно расчитать смертность, специфическую для каждого возраста (табл. 3.1, Гиляров, 1990).

Таблица 3.1

Статическая демографическая таблица женского населения Канады на 1980 г.
(по Krebs, 1985)

Такие таблицы представляют собой как бы временной срез через популяцию. Если в популяции не происходит существенных изменений в смертности и рождаемости, то статические и динамические таблицы совпадают.

Данные таблиц выживания позволяют построить кривые выживания, или их еще называют кривыми дожития, так как отражают зависимость количества доживших до определенного возраста особей от продолжительности этого интервала с самого момента отрождения организмов.

Выделяют три типа основных кривых выживания (рис. 3.1), к которым в той или иной мере приближаются все известные кривые.

Рис. 3.1. Различные типы кривых выживания (Deevey, 1950)

Кривая I типа, когда на протяжении всей жизни смертность ничтожно мала, резко возрастая в конце нее, характерна для насекомых, которые обычно гибнут после кладки яиц (ее и называют «кривой дрозофилы»), к ней приближаются кривые выживания человека в развитых странах, а также некоторых крупных млекопитающих.

Кривая III типа ¾ это случаи массовой гибели особей в начальный период жизни. Гидробионты и некоторые другие организмы, незаботящиеся о потомстве, выживают за счет огромного числа личинок, икринок, семян и т. п.

Моллюски, прежде чем закрепиться на дне, проходят личиночную стадию в планктоне, где личинки гибнут в огромных количествах, поэтому кривую III называют еще «кривой устрицы».

Кривая II типа (диагональная) характерна для видов, у которых смертность остается примерно постоянной в течение всей жизни. Такое распределение смертности не столь уж редкое явление среди организмов. Встречаются они среди рыб, пресмыкающихся, птиц, многолетних травянистых растений.

Реальные кривые выживания часто представляют собой некоторую комбинацию указанных выше «основных типов». Например, у крупных млекопитающих, да и у людей, живущих в отсталых странах, кривая I вначале круто падает за счет повышенной смертности сразу после рождения.

Сформулируйте экологические законы Б. Коммонера.

Американский эколог Барри Коммонер является автором ряда книг и известным социальным и политическим активистом. Коммонер родился в 1917 году. Он учился в Гарвардском университете и получил степень доктора в области биологии в 1941 году. Основной темой своей работы, Коммонер как биолог, избрал проблему разрушения озонового слоя.

Коммонер достаточно радикален в выборе решения многих проблем загрязнения окружающей среды.

Он является решительным сторонником использования возобновляемых источников энергии, особенно солнечной энергии, которая может децентрализовать энергопотребление предприятий и использовать свет в качестве альтернативного источника энергии для большинства потребителей.

Сформулированные американским экологом Б. Коммонером (1974 г.) в свободной беллетристической форме законы (не в том строгом смысле, как это принято в естествознании):

1) «Все связано со всем»; это означает, что живая динамика сложных и разветвленных экологических цепей образует, в конечном итоге, единую высокосвязанную систему; в абстрактном варианте это утверждение повторяет известное диалектико-материалистическое положение о всеобщей связи вещей и явлений; на более конкретном уровне оно выступает как обобщение кибернетического характера;

2) «Все должно куда-то деваться»; это неформальная перефразировка фундаментального физического закона сохранения материи; здесь Коммонер ставит одну из труднейших проблем прикладной экологии – проблему ассимиляции биосферой отходов человеческой цивилизации;

3) «Природа знает лучше»; этот закон вызывает в литературе наибольшую критику; это положение распадается на два относительно независимых тезиса: первый, солидаризирующийся с известным не о руссоистским лозунгом «Назад к природе», который сегодня не может быть принят как нереалистичный; второй, связанный с призывом к осторожности в обращении с природными экосистемами, важен и конструктивен;

4) «Ничто не дается даром»; этот экологический закон объединяет в себе три предыдущих закона; по Коммонеру, глобальная экосистема представляет собой единое целое, в рамках которой ничего не может быть выиграно или потеряно и которая не может явиться объектом всеобщего улучшения; все, что было извлечено из нее человеческим трудом, должно быть возмещено.

Платы по этому векселю нельзя избежать; она может быть только отсрочена».

Источник

Как долго живут биологические виды, прежде чем исчезнуть?

Величественный синий кит, находящийся на грани исчезновения, бороздит моря уже около 4,5 миллионов лет, а неандертальцы исчезли всего за несколько сотен тысяч лет. Но являются ли эти существа типичными для своих биологических родов? Как долго обычно живут виды, прежде чем они вымирают?

Ответ на этот вопрос не так прост, как кажется, и в этом в том числе виноваты мы, «человеки разумные». Из-за разрушения среды обитания, изменения климата и ряда других факторов растения и животные исчезают с планеты быстрее, чем обычно, за исключением пяти других моментов в истории. Некоторые эксперты говорят, что мы сейчас переживаем шестое событие массового вымирания. Но даже в более спокойные периоды истории Земли ответ варьировался в зависимости от конкретного вида, который вы изучаете. Согласно статье в журнале People & The planet, в среднем вид млекопитающих существует на Земле от 1 до 2 миллионов лет.

Однако это среднее значение верно не для всех геологических периодов и не для всех млекопитающих. Согласно исследованию 2013 года, опубликованному в журнале Integrative Zoology, средний показатель для млекопитающих кайнозойской эры (от 65 миллионов лет назад и по настоящее время) составляет 3,21 миллиона лет, при этом более крупные млекопитающие живут дольше, чем более мелкие. Для беспозвоночных продолжительность жизни вида еще более впечатляющая: они существуют на планете в среднем от 5 до 10 миллионов лет.

Все глобальные вымирания в истории Земли.

Однако некоторые эксперты не согласны с тем, сколько в среднем виды живут до вымирания, особенно если речь идет о животных, живших многие миллионы лет назад. Да, летопись окаменелостей документирует, когда вид появляется и когда он исчезает, но оставляет очень большую погрешность, потому что условия в те моменты должны быть идеальными для образования окаменелостей.

А такие условия не всегда присутствуют, и нередко более старые или новые найденные окаменелости отодвигают «день рождения» или смерти вида сразу на несколько миллионов лет. Поэтому такая «средняя температура по больнице» в любом случае оказывается не такой уж и полезной. Стюарт Пимм, ведущий эксперт по вымиранию и эколог в Университете Дьюка, сказал, что он предпочитает думать о вымирании с точки зрения того, сколько видов исчезает каждый день, месяц или год.

«Об этом легче думать с точки зрения… уровня вымирания, в основном потому, что есть виды, которые живут очень долго», — сказал Пимм. «Кроме того, есть другие виды, которые живут недолго. Поэтому средний показатель несет не так много информации, как вы думаете».

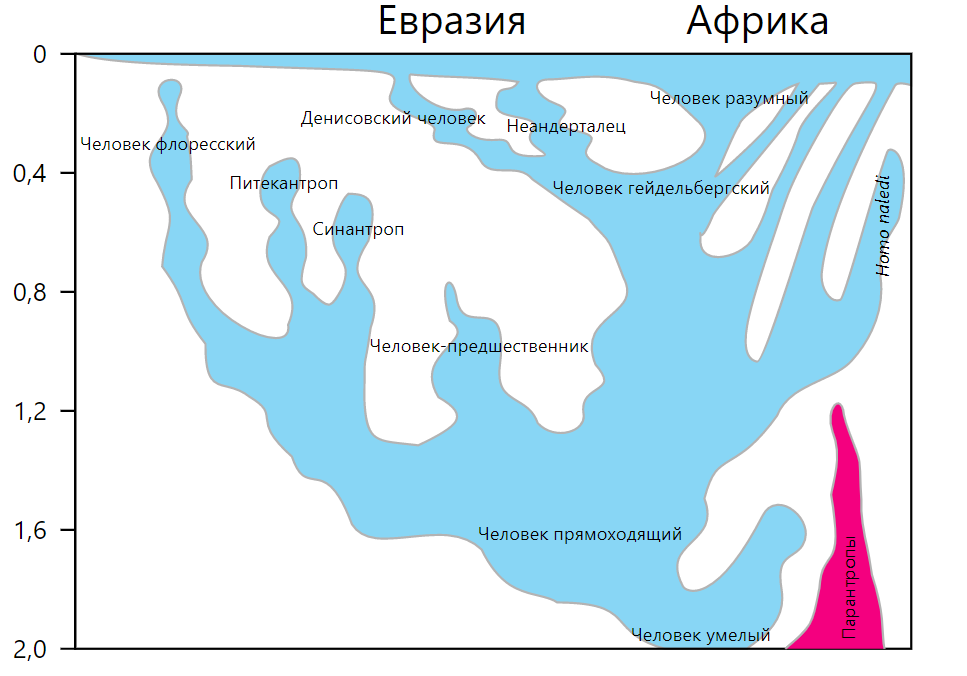
Хорошо видно, что даже в роду людей за 2 миллиона лет были потери видов.

Такой уровень смертности видов, называемый фоновым уровнем вымирания, является более достоверной величиной. По словам Пимма, если взять всю историю Земли, за исключением массовых вымираний, это число оказывается на уровне 1 вида на миллион в год. Иными словами, сейчас на нашей планете, согласно исследованию, опубликованному в журнале PLOS Biology, живет порядка 8.7 миллионов видов. И каждый год по различным причинам должно исчезать в среднем 8.7 штук.

При этом, по словам Пимма, текущая скорость вымирания гораздо выше, чем по 9 видов в год. Так, по данным Всемирного фонда дикой природы, сейчас в час вымирает по 3 вида, за день — около 70, за год больше 20 тысяч. Данные других исследователей колеблются от сотен до тысяч видов в год, что все равно ощутимо выше, чем в среднем за все время существования жизни на Земле.

Есть несколько причин, по которым оценки текущего уровня вымирания так сильно различаются. «Уровень вымирания зависит от того, сколько видов на данный момент существует на Земле и насколько быстро они исчезают», — сказал Тьерр Карри, старший научный сотрудник Центра биологического разнообразия в Орегоне. «И никто на самом деле не знает точного ответа ни на один из этих вопросов».

Эта достаточно большая рыбка, Phyllopteryx Dewysea, живет на побережье Западной Австралии и была обнаружена только в 2015 году. Так что мы и близко не знаем о всех видах, живущих на нашей планете.

По словам Пимма, около 90% живых организмов, в основном мелкие насекомые, вероятно, вообще не имеют научного имени. И если исследователи не знают о существовании вида, они не узнают, что он вымер. Еще одна сложность заключается в том, что бывает трудно определить, когда вид точно вымер. То, что исследователи не видели его представителей несколько лет, не означает, что они ушли навсегда. Расчеты становятся все труднее, особенно если вид вымер в дикой природе, но продолжают жить в зоопарках.

Эксперты сходятся во мнении, что современные темпы исчезновения слишком высоки. «Виды приспосабливаются так быстро, как могут», — сказал Пимм. «Но в конце концов удача отворачивается от них, и они не успевают адаптироваться достаточно быстро. И они уходят».

Источник

Продолжительность жизни вида

Продолжительность жизни вида зависит от условий (факторов) жизни. Различают физиологическую и максимальную продолжительность жизни.

Физиологическая продолжительность жизниопределяется только физиологическими возможностями организма. Теоретически она возможна, если допустить, что в период всей жизни организма на него не оказывают влияние лимитирующие факторы.

До максимальной продолжительности жизни может дожить лишь малая доля особей в реальных условиях среды. Эта величина варьирует в широких пределах: от нескольких минут у бактерий до нескольких тысячелетий у древесных растений (секвойя). Обычно, чем крупнее растение или животное, тем больше их продолжительность жизни, хотя бывают и исключения (летучие мыши доживают до 30 лет, это дольше, например, жизни медведя).

Данные таблиц выживания позволяют построить кривые выживания (дожития), так как они отражают зависимость количества доживших до определенного возраста особей от продолжительности этого интервала с самого момента от рождения организмов.

Выделяют три типа основных кривых выживания (рис. 2.1), к которым в той или иной мере приближаются все известные кривые.

Кривая I типа, когда на протяжении всей жизни смертность ничтожно мала, резко падая в конце, характерна для насекомых, которые обычно гибнут после кладки яиц (ее и называют «кривой дрозофилы»), к ней приближаются кривые выживания человека в развитых странах, а также некоторых крупных млекопитающих.

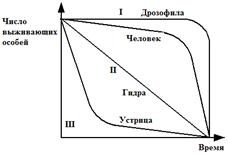
Кривая III типа – это случаи массовой гибели особей в начальный период жизни. Гидробионты и некоторые другие организмы, незаботящиеся о потомстве, выживают за счет огромного числа личинок, икринок, семян и т.п. Моллюски, прежде чем закрепиться на дне, проходят личиночную стадию в планктоне, где личинки гибнут в огромных количествах, поэтому кривую III называют еще «кривой устрицы».

Кривая II типа (диагональная) характерна для видов, у которых смертность остается примерно постоянной в течение всей жизни. Такое распределение смертности не столь уж редкое явление среди организмов. Встречаются они среди рыб, пресмыкающихся, птиц, многолетних травянистых растений.

Реальные кривые выживания часто представляют собой некоторую комбинацию указанных выше основных типов. Например, у крупных млекопитающих, да и у людей, живущих в отсталых странах, кривая I вначале круто падает за счет повышенной смертности сразу после рождения.

Экспоненциальная модель численности популяций

всемирно известной математической моделью, в основу которой положена задача о динамике численности популяции, является классическая модель Мальтуса. Это модель неограниченного роста – геометрическая прогрессия в дискретном представлении и экспоненциальная в непрерывном (Приложение 3, П.1):

→ , (2.5)

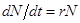
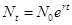
где N_t –численность популяции в момент времени; N₀– численность популяции в начальный момент времени t₀; r – показатель, характеризующий скорость размножения (прирост) особей в данной популяции. Экспоненциальный рост возможен только тогда, когда r имеет постоянное численное значение, так как скорость роста популяции пропорциональна самой численности.

Обсуждению важности вывода Мальтуса для популяционной динамики Ч. Дарвин посвятил несколько страниц своего дневника, указывая, что поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, препятствующие такому неограниченному размножению. Среди этих факторов может быть нехватка ресурса (продовольствия), вызывающая конкуренцию внутри популяции за ресурс, хищничество, конкуренция c другими видами. Результатом яв-ляется замедление скорости роста популяции и выход ее численности на стационарный уровень. Таким образом, экспоненциальный рост численности популяции – это рост численности ее особей в неизменяющихся условиях.

Условия, сохраняющиеся длительное время постоянными, невозможны в природе. Если бы это было не так, то, например, обычные бактерии могли бы дать такую массу органического вещества, которая могла бы покрыть весь земной шар слоем толщиной в два метра за два часа. Однако такого в природе не происходит, так как существует множество ограничивающих факторов. Но есть примеры, когда при замедлении роста, т.е. при снижении r, экспоненциальный рост сохраняется, может он возникать и на коротких отрезках жизни популяций.

Чтобы иметь полную картину динамики численности популяции, а также рассчитать скорость ее роста, необходимо знать величину так называемой чистой скорости воспроизводства(R₀), которая показывает, во сколько раз увеличивается численность популяции за одно поколение, за время его жизни Т:

(2.6)

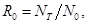
где N_T – численность нового поколения; N₀– численность особей предшествующего поколения; R₀– чистая скорость воспроизводства, показывающая также, сколько вновь родившихся особей приходится на одну особь поколения родителей. Если R₀= 1, то популяция стационарная и численность ее сохра­няется постоянной. Скорость роста популяции обратно пропорциональна длительности поколения:

(2.7)

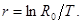
Из последнего выражения следует, что чем раньше происходит размножение организмов, тем больше скорость роста популяции. Это в равной степени относится и к популяции человека, отсюда – важность значения этой закономерности в демографической политике любого государства.

Впервые системный фактор, ограничивающий рост популяции, описал Ферхюльст в уравнении логистического роста:

. (2.8)

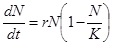
Это уравнение обладает двумя важными свойствами. При малых N численность х возрастает экспоненциально (как в уравнении 2.5) при больших – приближается к определенному пределу K, представляющему собой величину, называемую емкостью популяции, которая определяется ограниченностью пищевых ресурсов, мест для гнездования, многими другими факторами, которые могут быть различными для разных видов. Таким образом емкость экологической ниши представляет собой системный фактор,который определяет ограниченность роста популяции в данном ареале обитания.

Уравнение (2.8) можно также переписать в виде:

, (2.9)

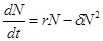
где δ –коэффициент внутривидовой конкуренции (за пищевой ресурс, убежища и т.п.). Решение уравнения (2.9) имеет вид:

(2.10)

Формула (2.10) представляет собой зависимость численности популяции от времени. Примеры экспериментально наблюдаемой динамики популяций, развивающихся по логистическому закону, приведены на рис. 2.2 а, б.

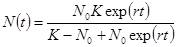
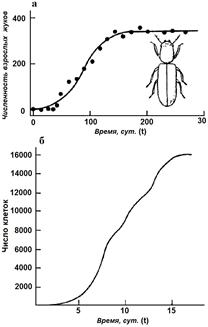
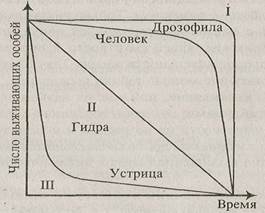
На рис. 2.2 а сплошной линией представлен график функции, которая описывается формулой (2.10). кривая N(t) имеет точку перегиба, с координатами:

Ордината представляет собой половину максимальной численности, а абсцисса зависит как от емкости популяции K, так и от константы собственной скорости роста r – чем выше генетические возможности популяции, тем скорее наступает перегиб на кривой численности.

Логистическая модель Ферхюльста (2.8) оказалась весьма перспективной. Исследование этого уравнения в случае дискретного изменения численности в популяциях с неперекрывающимися поколениями показало целый спектр возможных типов решений, в том числе колебательные изменения разного периода и вспышки численности.

При описании развития популяций следует отметить биологический факт, заключающийся в том, что в природе популяции имеют не только максимальную численность, определяемую величиной экологической ниши K, но и минимальную критическую численность L. При падении численности популяции ниже этой критической величины из-за неблагоприятных условий, или в результате хищнического промысла, восстановление популяции становится невозможным.

Величина нижней критической плотности различна для разных видов. Исследования биологов показали, что она может составлять всего лишь пару особей на тысячу квадратных километров в случае ондатры, и сотни тысяч особей для американского странствующего голубя. Заранее трудно было предположить, что столь многочисленный вид уже перешел через критическую границу своей численности и обречен на вымирание. Например, для голубых китов критическая граница численности оказалась равной десяткам-сотням. Хищническое истребление этих гигантских животных привело к тому, что их осталось слишком мало в Мировом океане. И хотя охота на них давно запрещена, надежд на восстановление популяции голубых китов практически нет. Кривые показателей численности для трех видов китов приведены на рис. 2.3.

(2.11)

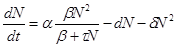
В формуле (2.11) первый член в правой части описывает размножение двуполой популяции, скорость которого пропорциональна квадрату численности (вероятности встреч особей разного пола) для малых плотностей, и пропорциональна числу самок в популяции – для больших плотностей популяции. Второй член описывает смертность, пропорциональную численности, а третий – внутривидовую конкуренцию, подобно тому, как это было в логистическом уравнении (2.9).

Зависимости численности от времени и скорости прироста от численности представлены на рис. 2.4 (а, б). Кривые 1-5 соответствуют различным начальным значениям популяции x. x = 0 и x = K – устойчивые стационарные состояния, x = L – неустойчивое, разделяющее области влияния устойчивых состояний равновесия. Величины L и K различны для разных популяций и могут быть определены из наблюдений и экспериментов.

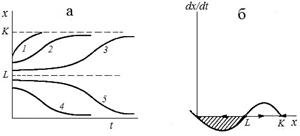Рис.2.4. Модель популяции с нижней критической численностью. Зависимость численности популяции от времени (а) и скорости роста от численности (б) для модели (2.11). Штриховкой обозначена область вырождения популяции.

Из рис. 2.4 (а) видно, что скорость восстановления популяции после ее падения в силу промысла или неблагоприятных условий зависит от того, насколько близка новая начальная численность к опасной границе L. Если ущерб, нанесенный популяции невелик (меньше половины емкости экологической ниши) популяция быстро восстанавливается по кривой 1, не имеющей точки перегиба. В случае, когда численность оставшейся популяции близка к критической, восстановление происходит сначала очень медленно, популяция надолго «застревает» вблизи опасной границы, а затем уже, «набрав силы», более быстро выходит на устойчивый стационарный уровень K (кривая 3). Кривая 2 представляет промежуточный случай. Кривые 4, 5 иллюстрирует вырождение популяции в случае, когда начальная численность опустилась ниже критической границы. обращает на себя внимание сходства начальных участков кривых 3 и 5. Близость к опасной границе со стороны больших значений (3) и меньших (5) выражается в долгом пребывании системы в неопределенном состоянии, когда малые флуктуации могут легко «перебросить» систему через опасную границу в «благополучную» область возврата к стационарному значению K,или, наоборот, в область вымирания.

В это время сторонний наблюдатель не сможет определить по форме кривой динамики численности, какая судьба ожидает систему. Для самих участников жизненной драмы – нахождения системы вблизи опасной границы – исход не очевиден. Важно понимать, что в этой ситуации чрезвычайно важны любые, даже очень малые усилия, направленные на преодоление критического барьера.

Именно популяции, численность которых близка к нижней критической численности, занесены в Красную книгу. Удастся ли перенести каждый конкретный вид на «Зеленые страницы», куда переносят виды, исчезновение которых удалось предотвратить, зависит от многих обстоятельств, в частности, как от репродуктивных усилий вида, так и от усилий людей, спасающих эти виды.

Анализ S – образной кривой (рис.2.2 (а) или рис.2.4 (а) кривая 2) показывает, что воздействие экологических факторов на скорость роста популя­ции может довести численность популяции до стабильной (r = 0), либо ее уменьшить, т.е. экспоненциальный рост замедляется или останавливается полностью и криваяэкспоненциального роста как бы вырождается в S-образнуюкривую.

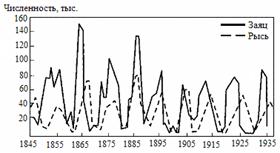
В природе так и происходит: экспоненциальный рост наблюдается какое-то достаточно корот- кое время, после чего ограничивающие факторы его стабилизируют и дальнейшее развитие популяции идет по логистической модели, что и описывается S-образной, логистической кривой роста популяции. Однако плато на S-образной кривой далеко не всегда бывает гладким, потому что колебания численности происходят постоянно, что отражается в виде колебаний кривой вокруг асимптоты «К» (рис. 2.5), эти колебания называются флуктуациями численности, которые могут быть сезонными и годовыми. Первые обусловлены абиотическими факторами, вторые – плюс к этому, еще и внутренними, биотическими. Колебания, вызванные биотическими факторами, называют осцилляциями 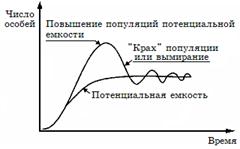(рис. 2.6), они отличаются высокой регуляцией и их даже называют циклами. Многие факторы, природные и антропогенные, вызывающие флуктуации, в значительной мере можно учесть, введя в формулу поправочные коэффициенты. Такие формулы позволяют прогнозировать реальный рост популяции живот ных и подобные процессы в демографии людского населения.

Уравнения, которые мы рассматривали до сих пор, предполагают, что процессы размножения и гибели происходят одновременно и популяция мгновенно реагирует на любое изменение внешних условий. Однако в реальности это не так. Всегда имеется некоторое запаздывание, которое вызвано несколькими причинами.

Развитие любой взрослой особи из оплодотворенного яйца требует определенного времени T. Поэтому если какое-нибудь изменение в окружающей среде, например, увеличение ресурса, вызовет внезапное повышение продуктивности взрослых особей, то соответствующе изменение численности произойдет лишь по прошествии времени T. Это означает, что уравнение

где N – численность взрослых особей, следует заменить уравнением:

где x_t-T – численность половозрелых особей в момент t-T.

В реальных популяциях интенсивность размножения и гибели различны в разных возрастных группах. Например, у насекомых откладывают яйца взрослые особи, а конкуренция наиболее выражена на личиночной стадии. Такие процессы, как отравление среды продуктами метаболизма, каннибализм и т.п. в наиболее сильной степени воздействуют на ранние возрастные стадии, а их интенсивность зависит от численности взрослых особей, т.е. отрицательное влияние на коэффициент естественного прироста оказывают особи предыдущего поколения. С учетом этих обстоятельств, логистическое уравнение (2.9) перепишется в виде:

Наиболее распространенное и изученное в динамике популяций уравнение Хатчинсона учитывает тот факт, что особи размножаются лишь с определенного возраста, и имеет вид:

(2.15)

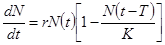
Смысл модели (2.15) заключается в том, что уровень лимитирования системы зависит не только от общей численности популяции в данный момент времени t, определяемой емкостью среды, но и от количества половозрелых особей в момент времени t-T. Еще более точное уравнение, учитываю-

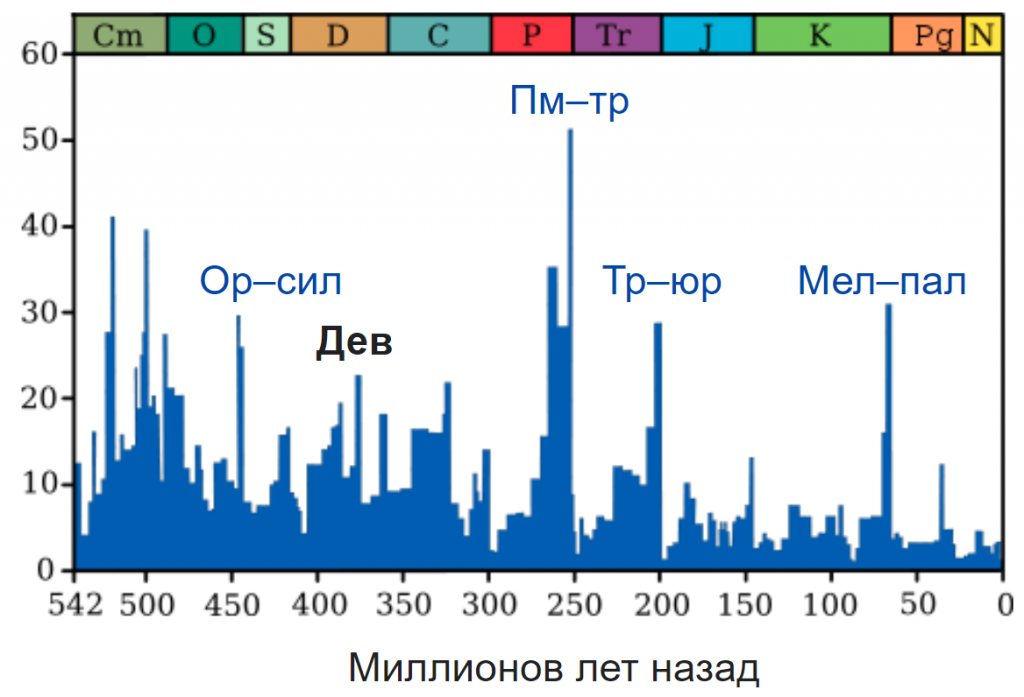
щее распределение времени запаздывания:

. (2.10)

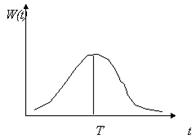
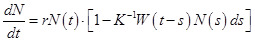
Вид функции распределения времен запаздывания W(t-s) представлен на рис. 2.7. Такого типа уравнения могут иметь колебательные решения.

В технике хорошо известно, что запаздывание в регуляции системы может привести к возникновению колебаний решения. Если система регулируется петлей обратной связи, в которой происходит существенная задержка, то весьма вероятно возникновение колебаний. Если продолжительность задержки в петле обратной связи больше собственного времени системы, могут возникнуть колебания с нарастающей амплитудой, нарушаются их период и фаза. Вопросы регуляции плотности и дискретные модели популяций даны в приложения 3, П.2, П.3.

Источник