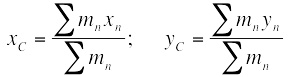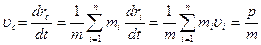Что понимают под аддитивность массы

Учебники

Журнал «Квант»

Общие

Масса

При воздействии одних тел на другие тела изменяют свою скорость — приобретают ускорение. При этом разные тела при данном воздействии приобретают разное ускорение (т. е. оказывают разное сопротивление изменению их скоростей).

Свойство тел приобретать определенное ускорение при данном воздействии называется инертностью. Инертность состоит в том, что для изменения скорости тела на заданную величину нужно, чтобы на него действовало другое тело и это действие длилось некоторое время.

Инертность — это свойство, присущее всем телам. Масса тела — количественная мера его инертности.

О теле, которое в результате взаимодействия меньше изменяет свою скорость, говорят, что оно более инертно, масса его больше:

В СИ единицей массы тела является килограмм (кг).

Так как масса входит в закон всемирного тяготения, то она определяет также гравитационное взаимодействие тел.

Установленная теорией относительности взаимосвязь между массой и энергией \(

W = mc^2\) показывает, что масса является мерой полной энергии тел.

Масса тела обладает свойством аддитивности (сложения): при соединении двух тел в одно массы этих тел складываются. Свойство аддитивности массы очень точно выполняется для макроскопических тел и нарушается лишь тогда, когда энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в атомное ядро.

Существуют два основных способа определения массы тела: 1) путем сравнения ускорений тела неизвестной массы и эталона массы при их взаимодействии (m_т = a_э m_э / a_т), 2) путем взвешивания на рычажных весах.

В классической механике Ньютона считают, что:

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 31-32.

Источник

Центр инерции. Аддитивность массы

Закон сохранения импульса и момента импульса

Координаты центра масс системы тел определяются следующим образом: (1)

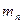
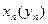
где и — массы и соответствующие координаты тел, входящих в систему.

Положение центра масс тела зависит от того, как распределяется по объему тела его масса. Центр масс не обязательно должен находиться в самом теле. Если тело движется поступательно под действием нескольких сил, значит, точка приложения равнодействующей этих сил находится в центре масс этого тела. Если направление прямой, вдоль которой действует сила, не проходит через центр масс тела, эта сила вызывает поворот тела.

При поступательном движении тела все его точки движутся с таким же ускорением, которое получает центр масс этого тела под действием равнодействующей внешних сил. Следовательно, для того чтобы описать поступательное движение тела, необходимо описать движение центра масс этого тела под действием равнодействующей внешних сил. При движении тела (механической системы) его центр масс движется так же, как двигалось бы под действием равнодействующей внешних сил материальная точка, имеющая массу, равную массе тела (системы). Поэтому, когда мы считаем тело материальной точкой, то имеем в виду центр масс данного тела.

Скорость центра масс механической системы равна отношению импульса этой системы к ее массе: (2)

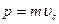
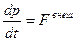
Соответственно импульс системы равен произведению ее массы на скорость центра масс: . Подставив это выражение для р в уравнение получим закон движении центра масс: (3)

Источник

Адиттивность масс системы. Закон сохранения массы

Вы будете перенаправлены на Автор24

Аддитивность масс системы

Поэтому (2) преобразуется в:

или на основании соотношения (1):

Масса составного тела равна сумме масс составляющих тел. Это свойство называется аддитивностью массы.

Закон сохранения массы

Готовые работы на аналогичную тему

Современный взгляд

В XX веке обнаружились два новых свойства массы:

масса физического объекта зависит от его внутренней энергии;

Закон сохранения массы получен как следствие галилеева принципа относительности. Но галилеев принцип относительности является приближенным предельным случаем эйнштейновского принципа относительности. Законы сохранения массы и энергии, которые в дорелятивистской физике считались двумя независимыми точными законами природы, в релятивистской физике утратили свою независимость и были объединены в единый закон сохранения массы-энергии.

Всякая энергия обладает массой, равной количеству энергии, деленному на квадрат скорости света в вакууме. То обстоятельство, что в химических реакциях не было обнаружено изменение массы вещества, связано с их относительно очень малым энергетическим выходом. Отсюда следует, что масса сохраняется только в изолированной системе, то есть при отсутствии обмена энергией с внешней средой.

Особенно ощутимо изменение массы при ядерных реакциях. Масса не является аддитивной величиной: масса системы не равна сумме масс ее составляющих. Примеры неаддитивности:

электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею как система;

масса дейтрона, состоящего из одного протона и нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц;

при термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия;

Примеры решения задач

Решение:

Молярная масса йодида натрия составляет:

\[m(NaI)=\nu (NaI)\cdot M(NaI)=1.7\cdot 150=2553\]

Решение: Кинетическая энергия тел до столкновения равна:

Кинетическая энергия тел после столкновения равна:

Тогда приращение кинетической энергии замкнутой системы равно:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 06 04 2021

Источник

Аддитивность

Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей.

Аддитивный (от лат. additio — прибавляю) — относящийся к сложению.

Содержание

Аддитивность в математике

Аддитивные величины в физике

В физике, аддитивность величины — когда величина чего-то равна сумме величин составных частей. Также такие величины называются экстенсивными, в отличие от интенсивных (например, температура и, как правило, плотность и т. п.).

Примеры аддитивных величин:

Свойство аддитивности для некоторых, нередко векторных, физических величин называется принципом суперпозиции:

Часто термин принцип суперпозиции подразумевает аддитивность полей, создаваемых источниками, в свою очередь аддитивными, и применяется к теориям, основные уравнения которых линейны.

Некоторые величины, такие как масса, скорость (относительное движение) или время (последовательные интервалы), допускают сложение в классической физике, но не в теории относительности.

Вообще в случае высоких или сверхвысоких энергий аддитивность как правило рано или поздно теряется, поскольку уравнения перестают быть линейными (а линейными являются лишь их низкоэнергетические приближения), однако принцип суперпозиции бывает полезен почти всегда в пределе слабых возмущений, а иногда оказывается справедливым для всего или почти для всего практически доступного диапазона величин. Теория же в этом случае сильно упрощается и может быть легче и лучше развита.

Аддитивные свойства в химии

Согласно ЭСБЕ, если смешать два совершенных (трудно сжижаемых, имеющих низкую критическую температуру) газа, то объем смеси окажется почти математически точно равным сумме объёмов смешанных газов; точно так же не изменятся при смешении их светопреломляющая способность, удельная теплоёмкость и т. д., и эти свойства такой смеси могут быть вычислены на основании свойств смешиваемых тел. Не то наблюдается, когда смешиваются между собою жидкости: сумма их объёмов обыкновенно не равна (больше, меньше) объёму смеси и т. д.; но иногда и здесь оказывается возможным вычислить (с достаточной степенью приближения к опытным данным) некоторые свойства смеси из свойств слагаемых, руководствуясь только правилом смешения и предполагая, что эти свойства при смешении не меняются. Подобные свойства называются, согласно предложению Оствальда, аддитивными (ср. Ostwald, «Allg. Ch.», 2-е изд. 1-й т., 1120—1122 [1891]). Математически строго аддитивны только массы смешиваемых тел, но иногда аддитивные объёмы, и если V есть объём смеси, а V1, V2, и т. д. объёмы смешиваемых жидкостей (жидкостей и твёрдых тел), то

а если смешиваются массы m1, m2, … и уд. объём (объём единицы массы) смеси есть v, а смешиваемых тел v1, v2 …, то

v(m1 + m2…) = v1m1 + v2m2 +…

или v = v1[m1/(m1 + m2)] + v2[m2/(m1 + m2)] +…;

иногда А. теплоёмкость смеси, и в таком случае с (уд. теплоёмкость смеси)

с = c1[m1/(m1 + m2)] + c2[m2/(m1 + m2)] + …,

где с1 и с2 уд. теплоёмкости смешиваемых тел, имеющих массы m1 и m2, или же, так как

процентному содержанию в смеси тела с массой m1, то

с = c1(p/100) + c2[(100 — p)/100]

Аддитивные методы в фотографии

Методы получения цветных изображений, основанные на аддитивном синтезе цветов. Методы цветной фотографии#Аддитивные методы

Аддитивные величины в быту и в экономике

Примером аддитивной величины можно считать деньги и другие материальные ценности, подлежащие количественному учету (хотя эффект их применения вообще говоря не аддитивен), а также рабочее время и так далее.

См. также

Примечания

Полезное

Смотреть что такое «Аддитивность» в других словарях:

АДДИТИВНОСТЬ — (от лат. additivus прибавляемый) свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, каким бы образом ни был разбит объект. Напр., аддитивность объема … Большой Энциклопедический словарь

аддитивность — (от лат. additio прибавление) свойство величин, заключающееся в том, что сумма значений величин, соответствующих частям объекта, равна значению величины, соответствующей целому объекту. Свойством А., например, обладает величина группы, но не… … Большая психологическая энциклопедия

аддитивность — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] аддитивность «Свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при… … Справочник технического переводчика

АДДИТИВНОСТЬ — (от латинского additivus прибавляемый), свойство объекта, по которому величина всего объекта равна сумме величин частей объекта при любом разбиении. Так, объем тела равен сумме объемов его частей … Современная энциклопедия

АДДИТИВНОСТЬ — (лат. addere добавлять) понятие, посредством которого обозначается нечто суммативное, не образующее органической цельности … Новейший философский словарь

АДДИТИВНОСТЬ — (от лат. additivus прибавляемый), тип отношений между к. л. целым и его частями, при котором свойства целого полностью определяются свойствами частей. Отношение А. часто выражают формулой «целое равно сумме частей». Примеры аддитивных… … Философская энциклопедия

АДДИТИВНОСТЬ — (от лат. additi vus прибавляемый) англ. additivity; нем. Additivitat. Свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, каким бы образом ни был… … Энциклопедия социологии

Аддитивность — [additivity] «свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части» (БСЭ. Т. 1, стр. 221). Соответственно … Экономико-математический словарь

Аддитивность — [лат. additio по­лучать путем сложения] – свой­ство, соответствующее целому объекту, равное сумме состав­ляющих его частей. [Ушеров Маршак А. В. Бетоноведение: лексикон. М.: РИФ Стройматериалы. – 2009. – 112 с.] Рубрика термина … Энциклопедия терминов, определений и пояснений строительных материалов

Аддитивность — (от латинского additivus прибавляемый), свойство объекта, по которому величина всего объекта равна сумме величин частей объекта при любом разбиении. Так, объем тела равен сумме объемов его частей. … Иллюстрированный энциклопедический словарь

Источник

Масса (физика)

Оглавление

Развитие концепции массы

Масса в классической механике

Примерно до середины 18 века были разработаны важные для сохранения количества движения и кинетической энергии, которые связаны с массой движущегося тела:

Переход на современную физику

В контексте классической физики, а значит, и в повседневной жизни применимы все пять вышеупомянутых свойств массы. В части теории относительности и квантовой физики влияние современной физики они имеют только приблизительно.

Таким образом, вышеупомянутые классические свойства массы могут оставаться в силе только приблизительно, а именно для классического или нерелятивистского предельного случая, т.е. ЧАС. для твердых тел с малой скоростью. В соответствии с требованиями специальной и общей теории относительности их необходимо переформулировать следующим образом:

Первоначальное значение массы как меры количества материи уже не может быть сохранено.

Устаревшие: «релятивистская масса» и «масса покоя».

Следовательно, невозможно увеличить массу системы только за счет ускорения.

Определение массы с использованием сохранения количества движения

п → 1 + п → 2 знак равно п → 1 + 2 <\ displaystyle <\ vec

> _ <1>+ <\ vec

> _ <2>= <\ vec

> _ <1 + 2>>

Это дает уравнение:

М. ( v → 1 ) ⋅ v → 1 + М. ( v → 2 ) ⋅ v → 2 знак равно 0 <\ Displaystyle М (<\ vec > _ <1>) \ cdot <\ vec > _ <1>+ M (<\ vec > _ <2>) \ cdot <\ vec > _ <2>= 0>

Отсюда следует, что в этой системе отсчета скорости двух одинаковых ударных тел должны быть противоположными и равными:

М. ( v → 1 ′ ) ⋅ v → 1 ′ + М. ( v → 2 ′ ) ⋅ v → 2 ′ знак равно М. 1 + 2 ( В. → ) ⋅ В. → <\ displaystyle M (<\ vec > _ <1>^ <\, '>) \ cdot <\ vec > _ <1>^ <\,'>+ M (<\ vec > _ <2>^ <\, '>) \ cdot <\ vec > _ <2>^ <\,'>= M_ <1 + 2>(<\ vec >) \ cdot <\ vec >>

Рассмотрение с классической физикой

Согласно преобразованию Галилея, действующему в классической физике, простое сложение скоростей применяется

Это уравнение между тремя скоростями совместимо с приведенным выше уравнением между тремя импульсами, только если

Рассмотрение с помощью релятивистской физики

Положительная и отрицательная эффективная масса

Массовая чаша

есть (вывод см. учетверенный импульс), энергия и импульс зависят от массы через соотношение энергии-импульса

единицы измерения

Для обозначения массы атомов и молекул широко используется атомная единица массы (u или amu).

Измерение

Прямое определение массы

Косвенное определение массы

м знак равно | Ф. → | | а → | <\ displaystyle m = <\ frac <| <\ vec > |> <| <\ vec > |>>>

Масса небесных тел также может определяться их гравитационным действием. Например, можно вычислить массу Солнца, используя закон всемирного тяготения, исходя из орбитальных данных планет, потому что их центральное ускорение зависит исключительно от массы и расстояния до центрального тела.

Связанные размеры

Классическая физика

Под тяжелой массой понимается как источник гравитационной силы, так и «гравитационный заряд». Сила, действующая на массу со стороны массы, равна М. s <\ Displaystyle М _ <\ mathrm >> м s <\ Displaystyle м _ <\ mathrm >>

Ф. → знак равно d п → d т <\ displaystyle <\ vec > = <\ frac <\ mathrm \ <\ vec

>> <\ mathrm t>>>

Специальная теория относительности

Определение массы как инварианта Лоренца

Релятивистская масса

Чтобы по-прежнему иметь возможность сохранять формулу Ньютона, был использован термин релятивистская масса.

м отн. знак равно м 0 <\ Displaystyle м _ <\ текст <отн.>> = м_ <0>> .

Последний упомянутый недостаток проистекает из определения силы как изменения количества движения во времени, то есть в специальной теории относительности: Ф. → <\ displaystyle <\ vec >>

Если сформировать размер и, следовательно, размер из этого ( v → ⋅ Ф. → ) <\ Displaystyle (<\ vec > \ cdot <\ vec >)>

это можно изменить после ускорения : а → <\ displaystyle <\ vec >>

а → знак равно 1 м Ф. → <\ displaystyle <\ vec > = <\ frac <1>> \ <\ vec >>

Энергия отдыха

Многочастичные системы

Для системы из нескольких невзаимодействующих частиц полная энергия и полный импульс являются суммой соответствующих размеров всех частиц. Следовательно, соотношение энергия-импульс имеет вид

Массовый дефект

Обеспечивает замкнутую систему с энергией за пределами системы, например. Б. в виде излучения снижается энергоемкость системы и, следовательно, ее масса. В этом смысле масса больше не является постоянной величиной в современной физике, хотя в повседневных ситуациях это практически незаметно.

Однако в ядерных реакциях преобразуется количество энергии, которым уже нельзя пренебрегать, по сравнению с энергией покоя основных компонентов. Энергия связи означает, что атомное ядро ​​имеет массу значительно меньшую, чем сумма его компонентов. Разница называется дефектом массы. Энергия связи большинства атомных ядер составляет от 7 до 9 МэВ на нуклон и, таким образом, вызывает дефект массы от 0,7 до 0,9 процента. Очень легкие атомные ядра ( 2 H, 3 H, 3 He, Li, Be, B) имеют более низкую энергию связи на нуклон от 1 до 6 МэВ и более низкие дефекты массы с 0,1 и 0,6 процента.

общая теория относительности

В общей теории относительности свободное падение тел в гравитационном поле понимается как бессиловое. Любые действующие силы могут привести к отклонению траекторий от свободного падения. Если тело не может свободно падать, требуется сила, размер которой пропорционален инерционной массе тела.

В основном уравнении общей теории относительности источником гравитации является тензор энергии-импульса, который состоит из плотности энергии, плотностей импульса, потоков энергии и потоков импульса. Поскольку энергия покоящихся тел определяется их массой, только их масса вызывает гравитацию. Если можно пренебречь движением тел, создающих гравитацию, и если скорость свободно падающих частиц мала по сравнению со скоростью света, тогда масса тел, создающих гравитацию, будет иметь эффект, как в теории гравитации Ньютона. Это ограничение не распространяется на свет как на пробную частицу: на солнце она отклоняется вдвое больше, чем можно было бы ожидать по Ньютону.

Происхождение масс элементарных частиц

Использование: масса и вес

При равенстве массы и веса может возникнуть впечатление, что масса зависит от силы тяжести, преобладающей на месте. Следующее утверждение вводит в заблуждение: «На Луне человек весом 60 кг весит всего около 10 кг». Более ясно: «Человек с« весом »на Земле 60 кг весит на Луне примерно столько же, сколько человек с «вес» 10 кг на Земле ».

Источник