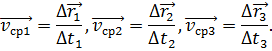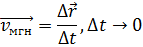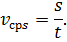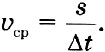Что понимают под мгновенной скорости неравномерного движения

Вопрос 2 § 5 Физика 9 класс Перышкин Что понимают под мгновенной скоростью неравномерного движения?

Помогите с ответом на вопрос
Что понимают под мгновенной скоростью неравномерного движения?

Под мгновенной скоростью неравномерного движения понимают скорость в конкретной точке траектории в данный момент времени.

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих ( Подробнее. )

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. ( Подробнее. )

Среди предложений 21-29:
(21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то ( Подробнее. )

Источник

Вопросы.

Прямолинейное равноускоренное движение относится к неравномерному движению, т.к. оно происходит с переменной (меняющейся во времени по величине и направлению) скоростью.

2. Что понимают под мгновенной скоростью неравномерного движения?

Под мгновенной скоростью неравномерного движения понимают скорость в конкретной точки траектории в данный момент времени.

3. Что называется ускорением равноускоренного движения?

4. Что такое равноускоренное движение?

Движение с постоянным ускорением называется равноускоренным движением.

5. Что показывает модуль вектора ускорения?

6. Что является единицей ускорения?

В СИ за единицу ускорения принимается ускорение такого равноускоренного движения, при котором за 1 секунду скорость тела изменяется на 1 м/с, т.е 1 м/с 2 (метр на секунду в квадрате или другими словами 1 метр в секунду за секунду).

7. При каком условии модуль вектора скорости движущегося тела увеличивается? уменьшается?

1. За один и тот же промежуток времени модуль вектора скорости первого автомобиля изменился от v₁ до v´, а второго- от v₂ до v´ (скорости изображены в одинаковом масштабе на рисунке 9). Какой из автомобилей двигался в указанный промежуток с большим ускорением? Скорость какого из них возрастала быстрее?

Из рисунка видно, что скорость первого автомобиля возрастала быстрее чем второго, а следовательно у него было большее ускорение.

2. Самолёт, разгоняясь перед взлётом, в течение некоторого промежутка времени двигался равноускоренно. Каково было при этом ускорение самолёта, если за 30 с его скорость возросла от 10 до 55 м/с?

3. С каким ускорением двигался поезд на некотором участке пути, если за 12 с его скорость возросла на 6 м/с?

Источник

Неравномерное движение. Мгновенная скорость

Урок 6. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Неравномерное движение. Мгновенная скорость»

Ранее мы рассматривали равномерное прямолинейное движение. Строго говоря, такое движение — это идеализированный пример. На самом деле тела двигаются неравномерно. Например, автомобиль едет чуть быстрее или чуть медленнее в определённые промежутки времени.

Да и траектория его никогда не является прямой на достаточно длинных участках.

Существует также колебательное движение, примером которого может являться движение маятника. Кроме того, как вы знаете, тело, находящееся в свободном падении, двигается с ускорением. Наконец, тело, двигающееся по кривой, обладает центростремительным ускорением. Все эти примеры являются примерами неравномерного движения. Неравномерным движением называется такое движение, при котором расстояния, пройденные за одинаковые промежутки времени, не равны.

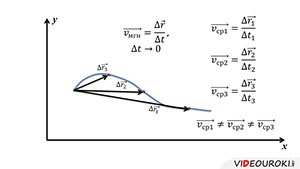
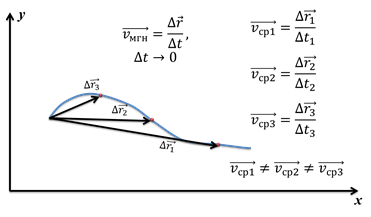
Именно, с неравномерным движением связано понятие мгновенной скорости. Чтобы понять, что такое мгновенная скорость, рассмотрим простой пример. На рисунке вы видите траекторию, по которой перемещается точка.

Отметим три случайных положения этой точки на траектории. Тогда мы можем найти три разных вектора перемещения: , и . Соответственно, эти перемещения были совершены за промежутки времени , и . Тогда мы можем посчитать средние скорости на этих участках:

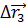
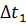
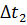
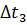
Очевидно, что эти скорости будут неравны. Но по мере уменьшения промежутка времени, средние скорости всё меньше и меньше будут отличаться друг от друга. В конце концов, если мы возьмём бесконечно малый промежуток времени, выражение

будет стремиться к определённому значению. То есть, это скорость в данный момент времени или, точнее сказать, мгновенная скорость.

Заметим, что какой бы сложной ни была траектория движения, если мы возьмём бесконечно малый промежуток времени, то на нём перемещение будет казаться прямолинейным. В этом случае, мы можем подсчитать скорость по формуле для прямолинейного движения. Но в каждое последующее мгновение, скорость будет меняться. Именно поэтому, она и называется мгновенной скоростью.

Мгновенная скорость — это величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

Мгновенная скорость направлена по касательной к траектории. Например, если вы едете в машине и наехали на кочку, то вас подбрасывает вверх. Почему? Потому что в тот миг, когда машина переезжает через кочку, мгновенная скорость направлена вверх. Но в следующее же мгновение, она направлена вниз, а еще через мгновение, скорость снова направлена также, как и была направлена до кочки.

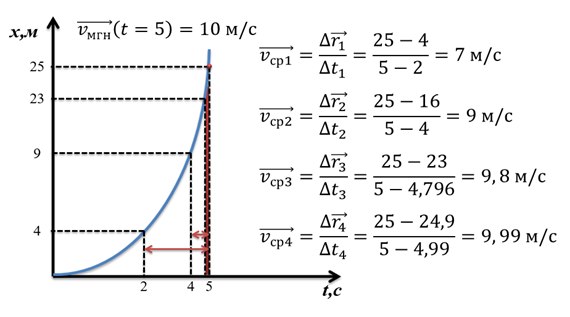
Рассмотрим конкретный пример. Вы видите график зависимости положения материальной точки от времени при равноускоренном движении.

График представляет собой параболу. Очевидно, что в каждой точке скорость разная. Если мы рассчитаем среднюю скорость в период от 2 до 5 секунд, то она будет равна 7 м/с. Рассмотрим теперь промежуток времени от 4 до 5 секунд. В этом случае, средняя скорость будет равна 9 м/с. Рассмотрим теперь участок от 4,796 секунд до 5 секунд. Этот промежуток времени довольно мал, поэтому если мы достаточно приблизим график, то траектория будет казаться почти прямой. Средняя скорость на этом участке равна 9,8 м/с.

Как видите, с уменьшением интервала времени, средняя скорость стремится к какому-то определённому значению. То есть, к значению мгновенной скорости в момент времени t = 5 с, которое в нашем случае равно 10 м/с. Если мы подсчитаем среднюю скорость на временном интервале, равным 0,01 с, то убедимся, что средняя скорость почти равна 10 м/с.

Заметим, что во всех упомянутых примерах мы рассматривали среднюю скорость перемещения. Существует также, такое понятие, как средняя путевая скорость. Именно путевая скорость чаще всего используется для описания движения.

Средняя путевая скорость определяется отношением пройденного пути к промежутку времени, за который этот путь пройден:

Мы уже говорили, что пройденный путь всегда больше либо равен модулю перемещения. Из этого можно сделать вывод, что средняя путевая скорость больше либо равна модулю средней скорости перемещения:

Источник

Неравномерное движение

В окружающем нас мире редкостью является равномерное движение тел, поскольку большинство объектов материального мира не способны двигаться с подобной точностью на протяжении длительного времени. Потому актуально использование понятия неравномерного движения тел.

Для характеристики такого вида движения используют понятия средней, мгновенной и средней путевой скоростей.

Характеристика средней скорости

Показатель средней скорости рассматривают на определённом отрезке пути, и рассчитывают таким образом:

Поскольку средняя скорость рассчитывается с использованием скалярных величин, то она также есть величиной скалярной.

Среднюю скорость также возможно рассчитать по формуле перемещения:

В этом случае она будет величиной векторной, поскольку рассчитывается через перемещение – векторную величину.

Не нашли что искали?

Просто напиши и мы поможем

Стоит различать эти две скорости. Несмотря на то, что они характеризуют одно и то же движение, данные величины имеют разный физический смысл.

Зачастую, вычисляя среднюю скорость, допускают некоторую погрешность, так как определяют среднюю скорость как среднее арифметическое. Суть заключается в том, что средняя арифметическая величина скорости тела на различных участках может отличаться от реального значения средней скорости тела, рассчитанной через преодоленный путь.

Непрерывное неравномерное движение тел сопровождается постоянным изменением их скорости. Это движение порождает закономерность, которая гласит, что скорость тела в любой следующей точке траектории не равняется его скорости в предыдущей.

Характеристика мгновенной скорости

Мгновенная скорость – это скорость объекта, которая фиксируется в конкретное время в конкретной точке.

Мгновенная скорость, рассчитанная через пройденный путь, есть величиной скалярной. Если она рассчитывается через перемещение, то является величиной векторной.

Характеристика средней путевой скорости

Различают еще одно понятие, характеризующее неравномерное движение – это средняя путевая скорость.

Поскольку средняя скорость – это вектор, который направлен в сторону перемещения тела, то модуль средней скорости принимает значение средней путевой скорости в том случае, когда тело не меняет направление своего движения. Если же тело меняет направление своего движения, модуль средней скорости уменьшается до средней путевой скорости.

Разновидности неравномерного движения

Движение тела может быть неравномерным по скорости и по направлению.

Существует несколько разновидностей неравномерного движения, среди них выделяют:

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Равнопеременным считается такое неравномерное движение, при котором скорость тела меняется на конкретную величину за равнозначные промежутки времени.

Движение тела, когда его скорость за любые равнозначные промежутки времени не меняется на конкретную величину, является неравнопеременным.

Если при равнопеременном движении скорость тела увеличивается, оно считается равноускоренным, если же скорость тела уменьшается – равнозамедленным.

Неравномерно движущееся тело может сочетать несколько вышеприведенных разновидностей.

Понятие ускорения

Рассчитывается таким образом:

Физический смысл ускорения заключается в том, что оно показывает на какую величину увеличивается или уменьшается скорость тела за единичный период времени.

Данная величина характеризует только равноускоренное или равнозамедленное движение, но не описывает равнопеременное движение, так как при этом не наблюдается взаимозависимость скорости и ускорения тела.
Ускорение со знаком «+» описывает равноускоренное движение, а со знаком «-» – равнозамедленное.
Уравнение ускоренного движения объекта записывается в следующем виде (для оси абсцисс):

С помощью данного уравнения рассчитывают скорость движения тела в любой промежуток времени.

Источник

Скорость при неравномерном движении

Конспект по физике для 8 класса «Скорость при неравномерном движении». Что такое мгновенная скорость. Как по графику скорости определить пройденный телом путь.

Скорость при неравномерном движении

В окружающем нас мире равномерное движение встречается нечасто. Обычно скорость тела изменяется с течением времени.

СРЕДНЯЯ СКОРОСТЬ НЕРАВНОМЕРНОГО ДВИЖЕНИЯ

В качестве примера неравномерного движения рассмотрим движение автобуса по шоссе. Начиная движение после остановки, автобус увеличивает свою скорость и, двигаясь далее, уменьшает свою скорость перед следующей остановкой. Он также может изменять скорость при пересечении перекрёстков, у светофора и т. п.

Необходимо чётко понимать, что когда мы говорим о скорости неравномерного движения, то имеем в виду скорость тела именно в данный момент времени. Однако если мы хотим охарактеризовать неравномерное движение в целом за данный промежуток времени, то вводится понятие средней скорости.

Средней скоростью неравномерного движения называют физическую величину, равную отношению пути, пройденного телом, ко времени, за которое этот путь был пройден:

При таком способе описания движения мы фактически заменяем неравномерное движение равномерным, скорость которого равна средней скорости неравномерного движения.

Так как средняя скорость равна отношению двух скалярных величин, она сама является величиной скалярной. Зная среднюю скорость неравномерного движения, можно делать выводы о том, насколько быстро или медленно движется тело.

МГНОВЕННАЯ СКОРОСТЬ

При движении тело проходит последовательно все точки траектории. В каждой точке оно находится в определённые моменты времени и имеет определённую скорость.

Скорость тела в данный момент времени или в данной точке траектории называют мгновенной скоростью.

Для уяснения смысла мгновенной скорости потребуются дополнительные рассуждения. Например, как определить мгновенную скорость автобуса в некоторый момент времени t, соответствующий началу торможения?

По мере уменьшения промежутков времени фактическое движение в пределах каждого отдельного промежутка времени будет всё меньше отличаться от равномерного, и наконец отличие перестанет улавливаться приборами.

В пределах малых промежутков времени, столь малых, что движение представляется равномерным, результат измерения можно относить к любому моменту времени в пределах рассматриваемого промежутка. Если движение равномерно, то его мгновенная скорость в любой момент времени равна скорости этого равномерного движения.

Для иллюстрации понятия мгновенной скорости Р. Фейнман использует пример с машиной, остановленной полицейским в момент превышения скорости. Если в данный момент времени мгновенная скорость равна, например, 90 км/ч, то это означает, что, если начиная с этого момента времени машина двигалась бы равномерно и прямолинейно, за следующую секунду она прошла бы 25 м, а в течение последующего часа — 90 км.

Интересно, что Галилей не пользовался такой физической величиной, как скорость. Рассуждения о природе движения проводились в виде анализа отношений однородных, имеющих одинаковую размерность величин. Впервые в современной форме записи скорость ввёл Л. Эйлер в 1765 г. в работе «Теория движения твёрдых тел». Он писал: «При равномерном движении отношение путей к промежуткам времени, в течение которых они проходятся, называется быстротой или скоростью…» Эйлер впервые записал υ = s/t, и эта форма записи с тех пор не изменилась.

ГРАФИК СКОРОСТИ И ЗНАЧЕНИЕ ПЕРЕМЕЩЕНИЯ

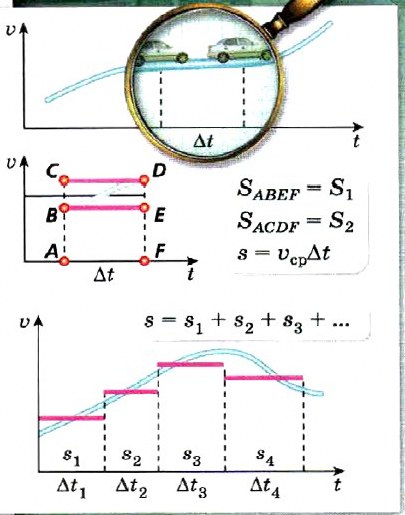
Мы уже знаем, что при равномерном движении модуль перемещения равен площади под графиком скорости. Оказывается, при неравномерном движении это равенство также справедливо. При этом не имеет значения, как изменяется скорость с течением времени.

Построим график зависимости скорости от времени и разобьём весь интервал движения на отрезки Δt. Рассмотрим движение тела в отдельном промежутке времени Δt. Как определить площадь фигуры под графиком? Очевидно, что эта площадь больше площади прямоугольника S₁ и меньше площади прямоугольника S₂ (S_ABEF = S₁; S_ACDF = S₂)

Если выбирать промежуток времени Δt всё меньше и меньше, то скорость на каждом промежутке времени будет меняться всё меньше и меньше и площади S₁ и S₂ будут отличаться всё меньше и меньше. Наконец, для каждого промежутка времени площадь под графиком станет равна произведению высоты (мгновенной скорости) и основания (промежутка времени), т. е. площадь равна перемещению тела за этот промежуток времени. А площадь под всем графиком равна сумме площадей для каждого промежутка времени, т. е. значение перемещения при неравномерном движении равно площади под графиком скорости.

Леонард Эйлер (1707—1783) — великий математик, механик и физик, швейцарец по происхождению. В 1727 г. переехал в Россию. Здесь работал в Петербургской академии наук.

Вы смотрели Конспект по физике для 8 класса «Скорость при неравномерном движении».

Источник