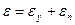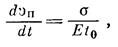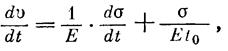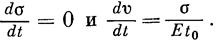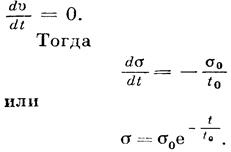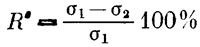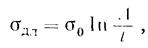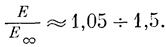Что понимают под периодом релаксации в горной породе

Реологические свойства горных пород

Под реологическими понимают свойства, характеризующие изменение всех механических характеристик породы при длительном воздействии на нее нагрузок, в том числе и нагрузок ниже предела упругости.

Одно из основных реологических свойств пород — ползучесть (крип) — явление постепенного роста деформации породы во времени при постоянном напряжении.

Внешне явление ползучести похоже на пластическое течение. Но последнее происходит только за пределами зоны упругости и при возрастающем напряжении, в то время как ползучесть может проявляться также при напряжениях, не превышающих предела упругости при достаточно длительном воздействии нагрузки.

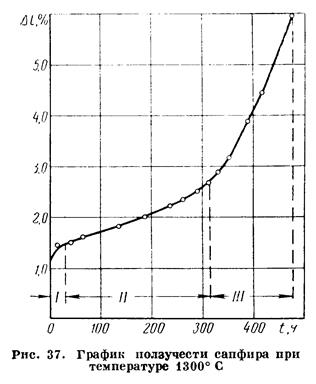
Идеальная кривая изменения деформации породы при длительном воздействии нагрузки состоит из трех отрезков, соответствующих трем основным стадиям деформации (рис. 37):

I — обычному процессу мгновенной деформации в момент нагружения породы;

II — установившемуся состоянию пластического течения при постоянной нагрузке (ползучести);

III — стадии возрастания скорости деформации и наступления момента разрушения породы.

Для анализа явления ползучести можно воспользоваться моделью тела Максвелла.

Если не превышен предел упругости, то общая деформация ε породы в любой отрезок времени состоит из двух составляющих — упругой деформации ε_у и деформации ползучести ε_п:

Скорость изменения деформации во времени:

Ввиду того что 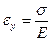, а составляющая ползучести является некоторой функцией напряжения:

где t₀ — постоянная, имеющая размерность времени.

Это равенство называется уравнением ползучести. Если напряжения σ постоянны, то

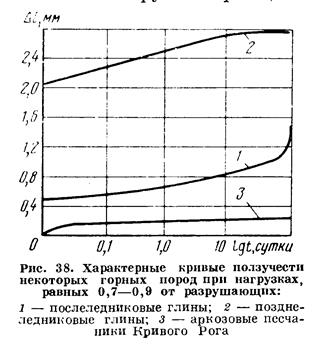
Связные породы (глины, аргиллиты, глинистые сланцы) обладают большим значением ползучести. Криворожские породы (кварцево-серицитовый сланец, гидрогематитовый роговик, аркозовый песчаник) обладают ползучестью, в среднем составляющей 20 — 35 % первоначальной мгновенной упругой деформации, причем наиболее значительные деформации происходят в течение первых 1,5 — 2 суток нагружения (рис. 38).

Ползучесть зависит от величины и направления приложения нагрузки на породу. Наибольшие деформации ползучести наблюдаются при нагрузках, приложенных перпендикулярно слоистости, причем отношение 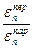достигает 1,4.

Явление, обратное ползучести, — постепенное снижение напряжений в породе при постоянной ее деформации — называется релаксацией напряжений. Релаксация представляет собой ползучесть при напряжении, которое уменьшается пропорционально нарастающей пластической деформации; упругие деформации, появившиеся в породе при первоначальном нагружении, постепенно переходят в пластические. В результате этого после снятия нагрузки образец не восстанавливает своей первоначальной формы, несмотря на то что исходные напряжения не превышают предел упругости породы.

При релаксации прирост деформаций во времени не происходит, поэтому предыдущее уравнение может быть написано как уравнение релаксационного процесса, если

В этом уравнении показатель t₀ равен времени, в течение которого напряжения в теле убывают в е раз, и называется периодом релаксации.

Период релаксации для большинства горных пород очень велик и поэтому для характеристики реологических свойств пород часто используют относительный показатель падения напряжения в породе R‘ за определенный период (неделя, месяц и т. д.):

где σ₁ — напряжения в испытываемом образце в момент приложения нагрузки; σ₂ — напряжения в образце по истечении определенного периода.

Рассмотрение ползучести и релаксации пород показывает, что существует общая закономерность изменения свойств пород со временем действия нагрузки — чем длительнее воздействие на породы нагрузки, тем слабее становятся упругие свойства пород, уменьшается предел упругости и тем сильнее проявляются их пластические свойства. Эта закономерность имеет весьма существенное значение, так как при разработке месторождений можно встретиться с самыми различными по длительности процессами воздействия нагрузок на породы, начиная от мгновенных (взрывание, откалывание, дробление) и кончая нагрузками, продолжающимися в течение нескольких лет (нагрузки на целики и кровлю подземных выработок, устойчивость отвалов и бортов карьеров).

Если длительность приложения нагрузки становится сравнимой с периодом релаксации породы, то порода приобретает пластические свойства. В результате этого возникают оползневые и просадочные явления, нежелательные перераспределения напряжений в массиве вследствие горного давления и разрушение целиков, выработок и т. д.

При длительном воздействии напряжений происходит постепенное снижение прочности горных пород (рис. 39).

В этом случае используют понятие «длительная (текущая) прочность». Нагрузка с увеличением времени воздействия уменьшается по определенной кривой, ассимптотически приближаясь к некоторому предельному значению, называемому пределом длительной прочности .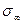

Длительная прочность 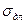значительно меньше стандартной прочности:

где σ₀ — прочность породы при мгновенном нагружении; А — константа, характеризующая стойкость породы; t— время приложения нагрузки.

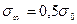
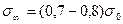
Для некоторых глин и мергелей Курской магнитной аномалии , для большинства других пород предел длительной прочности .

Модуль упругости при длительном воздействии нагрузок 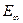также меньше Е. Обычно

Уменьшение прочности горной породы при увеличении времени воздействия нагрузки на практике характеризуется коэффициентом, равным отношению предела прочности на сжатие к некоторому значению длительной прочности (табл. 9).

При длительном воздействии нагрузки иногда происходит уплотнение (консолидация) глинистых пород. Это обусловлено выдавливанием из глин воды, уплотнением минеральных частиц, образованием новых, более устойчивых структурных связей, залечиванием микротрещин и дефектов. В результате этого прочность таких пород со временем может возрастать.

Учет реологических явлений в породах приобретает особое значение при разработке угольных месторождений на больших глубинах, так как уголь часто залегает в относительно слабых осадочных породах (глинистые сланцы, аргиллиты, алевролиты и т. д.), склонных к пластическим деформациям.

Дата добавления: 2016-10-26 ; просмотров: 4850 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Ползучесть и релаксация напряжения

Рассмотрим ползучесть и релаксацию напряжений, так как считается, что из всех механических свойств горных пород, связанных с их течением, именно они наиболее важны при образовании геологических структур.

«Ползучесть» (creep) определяется как явление, при котором деформация объекта возрастает со временем, когда объект долго подвергается воздействию постоянного напряжения, превышающего определенную величину (предел текучести). «Кривая ползучести» (creep curve) выражает эти отношения в виде зависимости деформации от времени. Процесс ползучести в общем можно разделить на три стадии. Первая стадия называется первичной или переходной ползучестью. Она следует за мгновенной упругой деформацией, и скорость деформирования со временем уменьшается, давая выпуклую кривую ползучести. Вторая стадия — стадия вторичной или равномерной ползучести, когда скорость деформации постоянна и кривая ползучести представляет собой прямую линию. В течение третьей стадии появляются и быстро развиваются трещины, так что скорость деформации возрастает и объект, наконец, разрушается. Эта стадия называется третичной или ускоренной ползучестью (рис. 6.3). Для изучения ползучести были выполнены многочисленные теоретические и экспериментальные работы на монокристаллах либо на образцах мономинеральных горных пород, например известняка.

Явление ползучести до некоторой степени можно установить в горных породах. Для объяснения первичной и вторичной ползучести обычно используется модель Бюргера (Burger’s model) (рис. 6.4). Эта модель представляет собой последовательное сочетание моделей Максвелла и Войгта (Кельвина). Когда к этой системе прилагается постоянное напряжение σ₀, взаимосвязь между деформаций ε и временем t выражается следующим уравнением

где γ и η — модуль упругости и коэффициенты вязкости; индексы М и V относятся к моделям Максвелла и Войгта.

При t = 0 это уравнение выражает упругую деформацию в виде ε = σ₀/γ_м, а при t = ∞ оно представляет вторичную ползучесть с постоянной скоростью деформации, задаваемой ε = σ₀/η_м. Пока t мало, это уравнение может выражать первичную ползучесть, когда ε постепенно уменьшается. В дополнение к этому уравнению для выражения напряжения и деформации ползучести были предложены различные формы уравнений, а именно показательные, логарифмическая и гиперболическая функции.

Сходство с ползучестью горных пород как с явлением можно до некоторой степени обнаружить в ползучести минералов, но действительные механизмы ползучести горных пород намного более сложны, чем механизмы ползучести минералов. Тем не менее, полагают, что ползучесть горных пород и формаций играет главную роль в образовании геологических структур, протекающем в течение огромных периодов времени.

Релаксация напряжения (stress relaxation) — другой важный фактор рассматриваемого явления. Релаксация обычно наблюдается на модели Максвелла либо на сложных моделях, в состав которых она входит. Это явление, когда при постоянной деформации напряжение постепенно уменьшается. Принимая модуль Юнга пружины за Е, вязкость амортизатора η, напряжение σ, а деформацию ε, реологическое уравнение модели Максвелла, показанной на рис. 6.5, можно записать следующим образом:

Если деформация системы теперь поддерживается постоянной и σ = σ₀ при t = 0, напряжение выражается как

и экспоненциально уменьшается со временем, Принимая t_e за время, необходимое, чтобы напряжение достигло 1/е от начального напряжения (е — основание натурального логарифма), можно записать

Это время называется временем релаксации (relaxation time).

Рассмотрим тектонические следствия релаксации напряжения. Григгс (1939) провел трехосные испытания при высоком давлении на известняке Соленхофен. Использовав данные испытаний ползучести, проводившихся 550 дней при температуре 23°С и дифференциальном напряжении 140 МПа, он рассчитал, что коэффициент вязкости этого известняка имеет значение 2,2·10 21 Па·с. Он предположил, что это значение, вероятно, соответствует минимальному уровню среднего значения коэффициента вязкости для пород, слагающих верхнюю часть земной коры. Кроме того, оно хорошо соответствует коэффициенту вязкости, полученному Гутенбергом (1941) при моделировании послеледниковых воздыманий Фенноскандии с использованием модели Максвелла. Итак, если η = 2,2·10 21 Па·с, E = 70 ГПа, тогда t_e = 1 млн лет. Прайс (1959) отметил, что это значение для η было, во-первых, получено для легкотекучей породы, т. е. известняка, и, во-вторых, что на нее на глубине будет влиять температура. Таким образом, он пришел к заключению, что время релаксации напряжения горных пород верхней части земной коры будет не менее 1 млн лет, а возможно, превысит 100 млн лет, и в этом случае время, необходимое, чтобы напряжение упало до 1 % от первоначального, будет около 50 млн лет.

Если этот вывод верен, он означает, что напряжение, действующее на определенную часть земной коры в определённое время, затем в течение чрезвычайно длительного периода времени будет продолжать существовать в качестве так называемого остаточного напряжения (residual stress). Например, влияние трех главных циклов орогенических движений, происходивших на Земле с палеозойской эры (а именно каледонской, варисской и альпийской эпох орогении), распространялось на интервалы около 15 млн лет, и последующие циклы возникали в ситуации, когда тектонические напряжения предшествовавших орогенических периодов, вероятно, все еще присутствовали. Это не имеет значения для механических аспектов тектонической истории, но фактических примеров конкретного изучения данного явления нет. Однако эта тема, вероятно, будет важной, областью исследований в будущем.

Источник

период релаксации напряжений в горной породе

127 период релаксации напряжений в горной породе

Параметр, равный времени, в течение которого напряжения в горной породе в результате релаксации убывают в е раз

127 период релаксации напряжений в горной породе

Параметр, равный времени, в течение которого напряжения в горной породе в результате релаксации убывают в е раз

Смотреть что такое «период релаксации напряжений в горной породе» в других словарях:

период релаксации напряжений в горной породе — Параметр, равный времени, в течение которого напряжения в горной породе в результате релаксации убывают в е раз. [ГОСТ Р 50544 93] Тематики горные породы Обобщающие термины физические свойства горных пород EN stress relaxation period DE… … Справочник технического переводчика

период — 2.18 период: Продолжительность времени. Источник: ГОСТ ИСО 8601 2001: Система стандартов по информации, библиотечному и издательскому делу. Представлен … Словарь-справочник терминов нормативно-технической документации

ГОСТ 30330-95: Породы горные. Термины и определения — Терминология ГОСТ 30330 95: Породы горные. Термины и определения оригинал документа: 161 абразивность горной породы Горно технологическое свойство, характеризующее способность горной породы изнашивать контактирующие с ней поверхности Определения… … Словарь-справочник терминов нормативно-технической документации

ГОСТ Р 50544-93: Породы горные. Термины и определения — Терминология ГОСТ Р 50544 93: Породы горные. Термины и определения оригинал документа: 161 абразивность горной породы Горно технологическое свойство, характеризующее способность горной породы изнашивать контактирующие с ней поверхности… … Словарь-справочник терминов нормативно-технической документации

Источник

Реологические свойства горных пород

Под реологическими понимают свойства, характеризующие изменение всех механических характеристик породы при длительном воздействии на нее нагрузок, в том числе и нагрузок ниже предела упругости.

Одно из основных реологических свойств пород — ползучесть (крип) — явление постепенного роста деформации породы во времени при постоянном напряжении.

Внешне явление ползучести похоже на пластическое течение. Но последнее происходит только за пределами зоны упругости и при возрастающем напряжении, в то время как ползучесть может проявляться также при напряжениях, не превышающих предела упругости при достаточно длительном воздействии нагрузки.

Идеальная кривая изменения деформации породы при длительном воздействии нагрузки состоит из трех отрезков, соответствующих трем основным стадиям деформации (рис. 37):

I — обычному процессу мгновенной деформации в момент нагружения породы;

II — установившемуся состоянию пластического течения при постоянной нагрузке (ползучести);

III — стадии возрастания скорости деформации и наступления момента разрушения породы.

Для анализа явления ползучести можно воспользоваться моделью тела Максвелла.

Если не превышен предел упругости, то общая деформация ε породы в любой отрезок времени состоит из двух составляющих — упругой деформации ε_у и деформации ползучести ε_п:

Скорость изменения деформации во времени:

Ввиду того что , а составляющая ползучести является некоторой функцией напряжения:

где t₀ — постоянная, имеющая размерность времени.

Это равенство называется уравнением ползучести. Если напряжения σ постоянны, то

Связные породы (глины, аргиллиты, глинистые сланцы) обладают большим значением ползучести. Криворожские породы (кварцево-серицитовый сланец, гидрогематитовый роговик, аркозовый песчаник) обладают ползучестью, в среднем составляющей 20 — 35 % первоначальной мгновенной упругой деформации, причем наиболее значительные деформации происходят в течение первых 1,5 — 2 суток нагружения (рис. 38).

Ползучесть зависит от величины и направления приложения нагрузки на породу. Наибольшие деформации ползучести наблюдаются при нагрузках, приложенных перпендикулярно слоистости, причем отношение достигает 1,4.

Явление, обратное ползучести, — постепенное снижение напряжений в породе при постоянной ее деформации — называется релаксацией напряжений. Релаксация представляет собой ползучесть при напряжении, которое уменьшается пропорционально нарастающей пластической деформации; упругие деформации, появившиеся в породе при первоначальном нагружении, постепенно переходят в пластические. В результате этого после снятия нагрузки образец не восстанавливает своей первоначальной формы, несмотря на то что исходные напряжения не превышают предел упругости породы.

При релаксации прирост деформаций во времени не происходит, поэтому предыдущее уравнение может быть написано как уравнение релаксационного процесса, если

В этом уравнении показатель t₀ равен времени, в течение которого напряжения в теле убывают в е раз, и называется периодом релаксации.

Период релаксации для большинства горных пород очень велик и поэтому для характеристики реологических свойств пород часто используют относительный показатель падения напряжения в породе R‘ за определенный период (неделя, месяц и т. д.):

где σ₁ — напряжения в испытываемом образце в момент приложения нагрузки; σ₂ — напряжения в образце по истечении определенного периода.

Рассмотрение ползучести и релаксации пород показывает, что существует общая закономерность изменения свойств пород со временем действия нагрузки — чем длительнее воздействие на породы нагрузки, тем слабее становятся упругие свойства пород, уменьшается предел упругости и тем сильнее проявляются их пластические свойства. Эта закономерность имеет весьма существенное значение, так как при разработке месторождений можно встретиться с самыми различными по длительности процессами воздействия нагрузок на породы, начиная от мгновенных (взрывание, откалывание, дробление) и кончая нагрузками, продолжающимися в течение нескольких лет (нагрузки на целики и кровлю подземных выработок, устойчивость отвалов и бортов карьеров).

Если длительность приложения нагрузки становится сравнимой с периодом релаксации породы, то порода приобретает пластические свойства. В результате этого возникают оползневые и просадочные явления, нежелательные перераспределения напряжений в массиве вследствие горного давления и разрушение целиков, выработок и т. д.

При длительном воздействии напряжений происходит постепенное снижение прочности горных пород (рис. 39).

В этом случае используют понятие «длительная (текущая) прочность». Нагрузка с увеличением времени воздействия уменьшается по определенной кривой, ассимптотически приближаясь к некоторому предельному значению, называемому пределом длительной прочности .

Длительная прочность значительно меньше стандартной прочности:

где σ₀ — прочность породы при мгновенном нагружении; А — константа, характеризующая стойкость породы; t— время приложения нагрузки.

Для некоторых глин и мергелей Курской магнитной аномалии , для большинства других пород предел длительной прочности .

Модуль упругости при длительном воздействии нагрузок также меньше Е. Обычно

Уменьшение прочности горной породы при увеличении времени воздействия нагрузки на практике характеризуется коэффициентом, равным отношению предела прочности на сжатие к некоторому значению длительной прочности (табл. 9).

При длительном воздействии нагрузки иногда происходит уплотнение (консолидация) глинистых пород. Это обусловлено выдавливанием из глин воды, уплотнением минеральных частиц, образованием новых, более устойчивых структурных связей, залечиванием микротрещин и дефектов. В результате этого прочность таких пород со временем может возрастать.

Учет реологических явлений в породах приобретает особое значение при разработке угольных месторождений на больших глубинах, так как уголь часто залегает в относительно слабых осадочных породах (глинистые сланцы, аргиллиты, алевролиты и т. д.), склонных к пластическим деформациям.

Теплопроводность пород

Теплопроводность пород определяет способность минералов, слагающих породу, проводить тепло.

У чистых монокристаллов теплопроводность наибольшая, а при переходе их в поликристаллы она падает (табл. 10).

Наибольшие пределы изменения теплопроводности характерны для монокристаллов.

Для практических расчетов, теплопроводности пород, представляющих собой статистическую смесь минералов, пригодна формула логарифмического средневзвешенного

Значения теплопроводности различных минералов, составляющих породу, имеют небольшие различия, поэтому для упрощения расчетов можно принять среднее значение теплопроводности

,

где — теплопроводность слоистой породы вдоль напластования;

— теплопроводность слоистой породы поперек напластавания.

Теплопроводности кристаллических и аморфных минералов имеют значительные отличия. Как правило, λ_кр > λ_ам.

Теплопроводность аморфных минералов не превышает 1,5 ккал/м·ч· 0 С, поэтому наличие стекловатой массы понижает теплопроводность пород.

Теплопроводность пород зависит от размеров зерен, из которых сложены породы. Как правило, происходит уменьшение теплопроводности пород с уменьшением размеров зерен. Влияние размеров зерен наиболее существенно только при небольших их средних размерах d_ср. Это объясняется тем, что длина свободного пробега фононов определяется двумя факторами: рассеиванием фононов на фононах и рассеиванием фононов на границах кристаллов и зерен. Какой фактор будет преобладать, зависит от соотношения длины свободного пробега фононов и размеров зерен d_ср. Если l 0 C B=0,0027).

При этом анизотропия объясняете тем, что частицы, входящие в кристаллическую решетку минерала, вдоль слоистости взаимодействуют интенсивнее; молекулярное движение перпендикулярно плоскости спайности передается значительно хуже.

Теплопроводность пористых пород является сложной функцией составляющих их фаз (табл. 12). При этом передача тепловой энергии может происходить как посредством теплопроводности, так и путем конвекции заполнителя порового пространства. Если размеры пор сравнительно малы, явление конвекции можно не учитывать, так же как и явление передачи тепла излучением, когда температура нагрева породы не превышает 1000° С.

Большую роль играет форма пор в породе; теплопроводность пород, имеющих удлиненные поры (типа трещин), значительно меньше в направлении, перпендикулярном направлению теплового потока. В этом случае можно использовать формулу последовательного соединения звеньев.

Так как коэффициент теплопроводности воздуха λ_в ≈ 0,02 ккал/м·ч· 0 С

Если тепловой поток направлен вдоль трещин, то

Поскольку

.

Эти уравнения определяют предельные зависимости теплопроводности пород от пористости и трещиноватости (рис. 41). В зависимости от формы пор тип конкретного уравнения может быть различным.

Для практических целей при Р около 20% можно пользоваться уравнением типа

Увлажнение пористых пород приводит к увеличению их теплопроводности (рис. 42); поскольку теплопроводность воды ниже, чем минералов, то λ пористой влажной породы никогда не становится близким или равным λ₀ такой же, но малопористой породы.

Исследования показывают, что теплопроводность заполняющего поры вещества (вода и воздух) может быть выражена следующей приближенной формулой (см. рис. 42):

,

С повышением температуры (рис. 43, а) теплопроводность почти всех кристаллических минералов и пород снижается, а теплопроводность аморфных и скрытокристаллических минералов и пород (обсидиан, аморфные разновидности SiO₂) повышается. Некоторый рост теплопроводности наблюдается также у анортозитов, глин и углей.

Наиболее значительное снижение λ, с повышением температуры характерно для пород, обладающих исходными его значениями. Эта закономерность хорошо согласуется с известной зависимостью (рис. 43, 6)

,

Такая закономерность четко соблюдается только в области температур до 400 0 С. При более высоких температурах λ → const, у некоторых пород наблюдается даже возрастание λ, с повышением температуры, так как при высоких температурах возникает дополнительная теплопроводность, обусловленная излучением.

Теплопроводность пород, обладающих повышенной пористостью (известняков и др.) с увеличением температуры изменяется мало, что также связано в основном с радиационной составляющей теплопроводности. В практических расчетах можно принять, что теплопроводность этих пород не зависит от температуры.

Уменьшение теплопроводности пород с повышением температуры объясняется усилением хаотичности движения молекул в кристаллической: решетке и их взаимодействием (рассеиванием одного фонона другим), что в свою очередь, снижает длину свободного пробега фононов.

Понижение температуры влажных пород ниже нуля приводит к замерзанию воды и, следовательно, к резкому возрастанию теплопроводности пород (так как λ_льда>> λ_в). Теплопроводность пористых пород под воздействием давления обычно увеличивается, непори­стых пород — увеличивается незначительно.

Основные понятия электродинамики

Электродинамика горных пород изучает взаимодействие электрических и магнитных полей с горной породой.

Электрическое поле проявляется в силовом воздействии на заряженные тела и частицы. Величина и направление действия электрических сил в любой точке пространства определяются напряженностью электрического поля .

Электрическое поле характеризуется также работой, которую оно может совершить. В качестве показателя этой работы принято пользоваться потенциалом φ. Разность потенциалов между двумя точками поля называется напряжением U.

Напряженность поля зависит от свойств среды, влияние которой учитывается, например, в законе Кулона о силе взаимодействия двух зарядов Q₁ и Q₂ :

где ε_а — коэффициент, учитывающий свойства среды и называемый абсолютной диэлектрической проницаемостью; r — расстояние между зарядами.

Так как из соотношения напряженности поля в вакууме Е₁ и в породе Е₂ получим:

Относительная диэлектрическая проницаемость показывает, во сколько раз напряженность поля в породе меньше, чем в вакууме.

Для характеристики электрического поля независимо от свойств вещества используют электрическую индукцию , величина которой для поля точечного заряда определяется только величиной заряда Q:

,

Как известно, проводники характеризуются тем, что всякое электрическое поле вызывает в них движение зарядов, а диэлектрики — полным отсутствием свободного движения зарядов.

Понятие диэлектрической проницаемости имеет смысл только для второй группы пород. Действительно, если среда, в которой располагаются заряды, способна проводить ток, то вместо взаимодействия зарядов будет происходить их перенос из точки с наибольшим потенциалом в точку с наименьшим потенциалом до момента их выравнивания. Следовательно, внутри проводника φ = const, = 0, а диэлектрическая проницаемость близка к бесконечности.

Перенос зарядов из одной точки проводника в другую, осуществляемый электронами и ионами, называется током проводимости. Ток — величина скалярная. Векторный показатель, характеризующий количество элементарных зарядов, проходящих через единицу сечения проводника в единицу времени, называют плотностью электрического тока :

,

где п — число заряженных частиц в 1 см 3 ; q— заряд частицы; υ— скорость направленного движения зарядов.

Так как υ= иЕ, где и — подвижность частиц, то

.

Это уравнение представляет собой закон Ома в дифференциальной форме, причем коэффициент ζ = пqи зависит от вида и состояния проводящей породы и называется ее удельной электропроводностью. Удельная электропроводность измеряется в сименсах (1/ом∙м).

Горные породы в большинстве случаев входят в группу полупро­водников, характеризующуюся свойствами как диэлектриков (ε 0).

Поляризация пород

При наложении на породу электрического поля в ней происходит смещение внутренних связанных зарядов — сдвижение центров положительных и отрицательных зарядов в кристаллах таким образом, что на поверхности породы появляются неуравновешенные связанные заряды. Эти заряды создают электрическое поле, направленное противоположно внешнему полю и ослабляющее его. Это явление называется поляризацией породы. Вектор поляризации — суммарный электрический момент единицы объема диэлектрика. Формально поляризацию можно представить как разность между истинной электрической индукцией поля и электрической индукцией, этого же поля в вакууме при = соnst:

Таким образом, ε — это мера поляризации породы; действительно, если Р = 0, то ε = 1:

.

Поляризация происходит только за счет смещения (или поворота) связанных зарядов.

В роли связанных зарядов могут выступать как атомы и ионы кристаллической решетки с гомео- и гетерополярной связью, так и целые объемы породы, оказавшиеся в особых структурных условиях.

В зависимости от механизма поляризации и частиц, участвующих в поляризации, выделяют четыре вида поляризации.

1. Электронная поляризация Р_Эвозникает при воздействии внешнего поля в атомах в результате смещения электронных орбит относительно положительно заряженных ядер (рис. 54, I).

Возникший электрический диполь может быть охарактеризован дипольным моментом — вектором, направленным от отрицательного заряда диполя к положительному и численно равным произведению заряда полюса диполя Qна расстояние между полюсами :

.

3. Дипольная ориентационная поляризация Р_Д(рис. 54, II) наблюдается при наличии в породах полярных связей ионов; в этом случае каждая молекула с момента своего возникновения уже имеет некоторый дипольный момент, не зависящий от напряженности внешнего поля. Однако в некотором объеме породы из-за хаотического расположения молекул суммарный дипольный момент при отсутствии внешнего поля равен нулю.

Если такую породу внести во внешнее электрическое поле, то диполи будут ориентироваться по силовым линиям внешнего поля и при этом будет поляризоваться весь объем породы. У жидкостей, где связи между отдельными молекулами слабы, ориентация диполей будет почти полной и слабо зависящей от напряженности электрического поля.

В твердых горных породах взаимные связи между молекулами не позволяют ориентироваться им точно по силовым линиям поля — диполи только поворачиваются на некоторый угол, зависящий от сил связей в данной породе и напряженности внешнего поля. Очевидно, что при увеличении угол поворота диполей до некоторой степени возрастает (квазиупругая поляризация).

4. Макроструктурная (объемная) поляризация Р_м возникает в многофазной системе, состоящей из кристаллов, обладающих различными электрическими свойствами, и пустот, заполненных жидкостью и воздухом (рис. 54, III).

При внесении породы в электрическое ноле свободные электроны и ионы, содержащиеся в проводящих и полупроводящих включениях, начинают перемещаться в пределах каждого включения. В результате этого каждое включение приобретает дипольный момент и ведет себя подобно большой молекуле. Это явление обусловлено электронным или ионным током проводимости в пределах каждого включения, но так как передвижение зарядов ограничено размерами включения, то конечный результат подобен явлению поляризации.

Поскольку время установления дипольной и макроструктурной поляризации пород сравнимо с частотой применяемых на практике электромагнитных полей, то эти два вида поляризации называются релаксационными или медленными, в отличие от мгновенного смещения электронов и ионов.

5. В горных породах имеет место также медленная электрохимическая поляризация, причиной которой являются следующие процессы, возникающие при прохождении тока через многофазные среды:

— окислительно-восстановительные процессы (характерны для сульфидов, окислов и высококарбонизированных каменных углей);

— процессы, характеризующиеся появлением в местах выхода и входа тока продуктов электролиза, газов;

— электроосмос, т. е. перемещение молекул жидкости, имеющих заряд одного знака, к электроду противоположной полярности;

— электрофорез — смещение твердых частиц, имеющих обратный знак заряда, к другому электроду;

— перераспределение концентрации растворов — например, в результате прохождения тока через кварцевый песок, насыщенный раствором NaС1, на положительном электроде появляется повышенная концентрация раствора.

Такие процессы бывают как обратимые, так и необратимые.

Электрохимическая поляризация происходит значительно медленнее, чем другие виды поляризации. У углей она достигает наибольшего значения в течение нескольких десятков минут.

При отключении напряжения в образце возникает ток деполяризации, направленный против приложенной разности потенциалов. Наиболее активными в этом отношении минералами являются пирит, пирротин, халькопирит и графит. Активны также магнетит, гематит и другие окислы, имеющие металлическую проводимость.

Под воздействием электрического поля в породах возникает явление электрострикции. Оно заключается в деформировании (подобно всестороннему сжатию) диэлектриков электрическим полем и присуще всем породам. Причинами электрострикции являются, с одной стороны, давление на породу заряженных частиц, создающих поле и притягивающихся друг к другу, с другой стороны — смещение ионов и электронов в породе, вызываемое полем.

Механические напряжения σ, возникающие в результате электрострикции, прямо пропорциональны квадрату напряженности электрического поля.

Источник