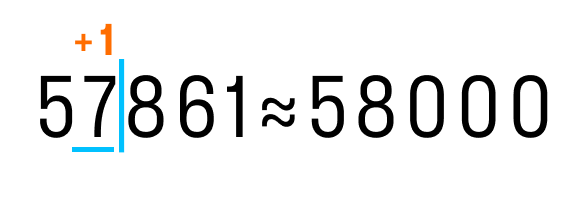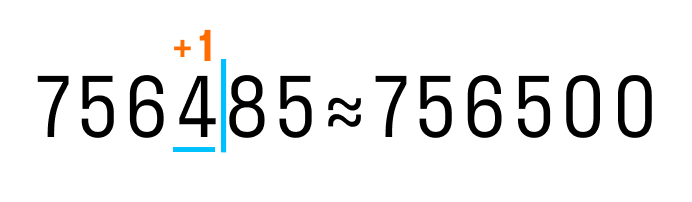Что понимают под термином округлить число
Округление
Округление — математическая операция, позволяющая уменьшить количество знаков в числе за счёт замены числа его приближённым значением с определённой точностью.
Содержание
Методы
В разных сферах могут применяться различные методы округления. Во всех этих методах «лишние» знаки обнуляют (отбрасывают), а предшествующий им знак корректируется по какому-либо правилу.
Варианты округления 0,5 к ближайшему целому
Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:
Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.
Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм. Так, если в реестре из 10000 строк окажется 100 строк с суммами, содержащими в части копеек значение 50 (а это вполне реальная оценка), то при округлении всех таких строк «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.
Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.
Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.
Применения
Округление используется для того, чтобы работать с числами в пределах того количества знаков, которое соответствует реальной точности параметров вычислений (если эти значения представляют собой измеренные тем или иным образом реальные величины), реально достижимой точности вычислений либо желаемой точности результата. В прошлом округление промежуточных значений и результата имело прикладное значение (так как при расчётах на бумаге или с помощью примитивных устройств типа абака учёт лишних десятичных знаков может серьёзно увеличить объём работы). Сейчас оно остаётся элементом научной и инженерной культуры. В бухгалтерских приложениях, кроме того, использование округлений, в том числе промежуточных, может требоваться для защиты от вычислительных ошибок, связанных с конечной разрядностью вычислительных устройств.
Использование округлений при работе с числами ограниченной точности
Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного действительного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах ошибки измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.
Эмпирические правила арифметики с округлениями
В тех случаях, когда нет необходимости в точном учёте вычислительных погрешностей, а требуется лишь приблизительно оценить количество точных цифр в результате расчёта по формуле, можно пользоваться набором простых правил округлённых вычислений [1] :
Несмотря на нестрогость, приведённые правила достаточно хорошо работают на практике, в частности, из-за достаточно высокой вероятности взаимопогашения ошибок, которая при точном учёте погрешностей обычно не учитывается.
Ошибки
Довольно часто встречаются злоупотребления некруглыми числами. Например:
Правильное округление чисел
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
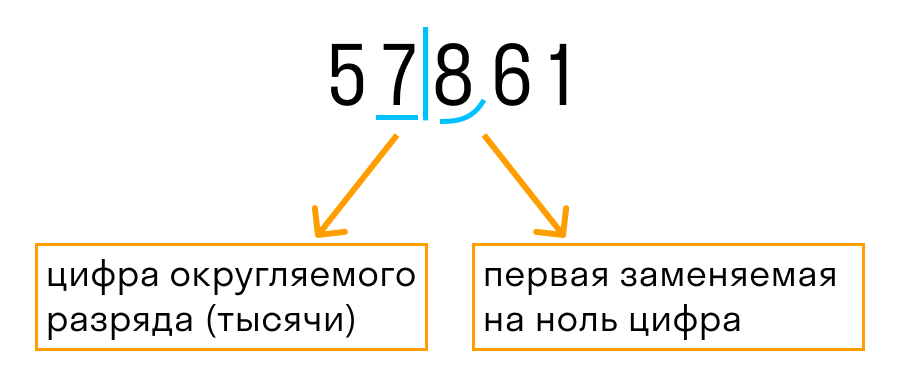
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
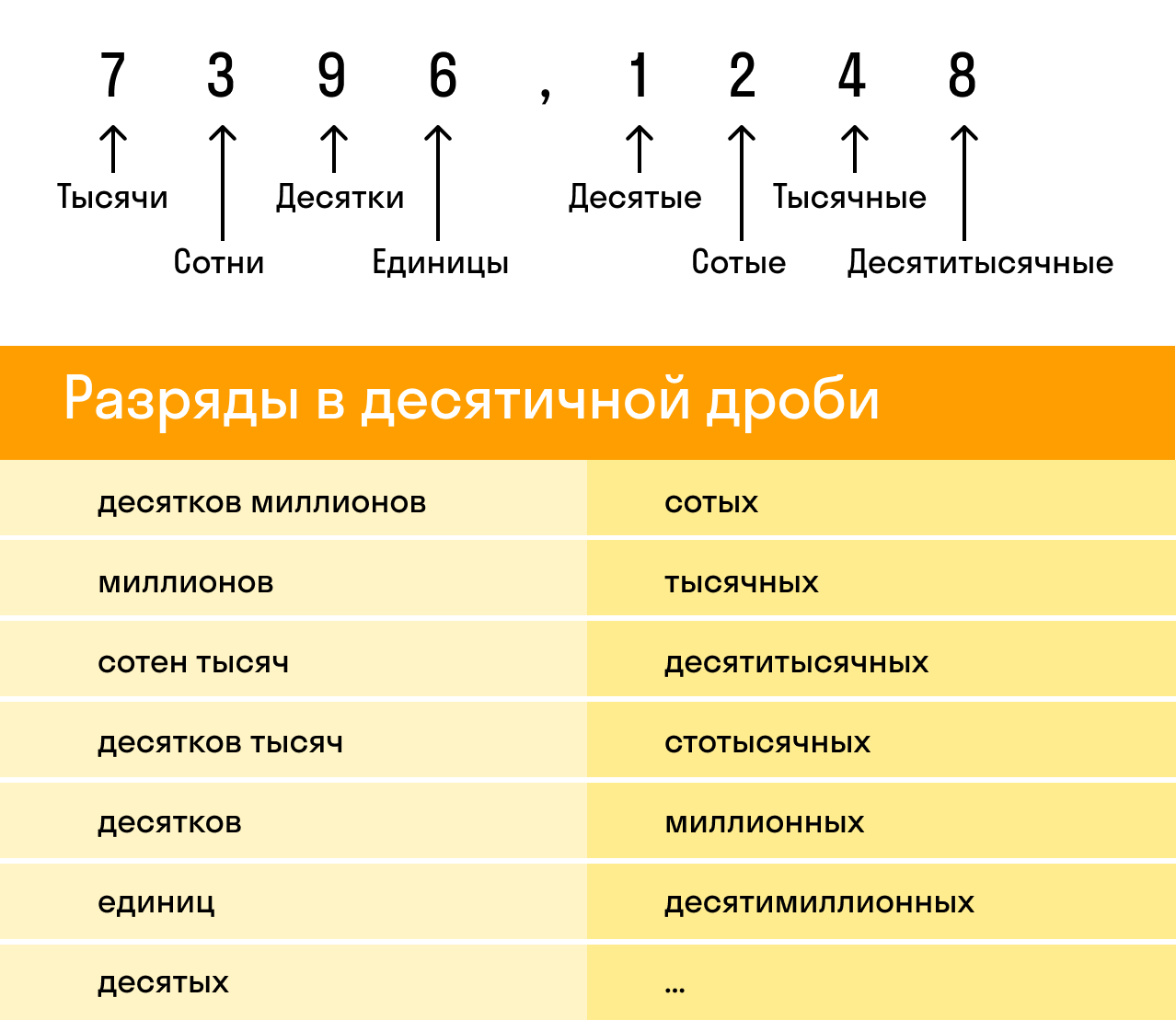
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
Разряды дробной части:
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Как правильно округлять числа после запятой
Далеко не все умеют округлять числа правильно. Например, купив товар за 1469 рублей, чаще всего люди говорят, что потратили полторы тысячи. В целом это так, но некоторые правила округления нарушаются. Чтобы этого избежать, мы с вами поговорим о том, как правильно работать с числами.
Зачем нужно округление
Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.
Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:
Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.
Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.
Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.
Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.
Правила округления чисел
В основе округления лежат математические правила:
В метрологии — науке об округлениях и погрешностях, результат принято округлять до двух значащих цифр. Что же это значит? Значащая цифра — это цифра от первой, отличной от нуля.
Есть три случая, для которых есть свои особенности округления:
Когда мы имеем дело с числами меньше единицы, необходимо округлять результат до двух знаков после запятой. Например, число 0,7342. Округляем это число до 0,734, а потом до 0,73. Именно так и должен быть округлён результат. Первый ноль не является значащей цифрой.
Попробуем округлить 8,357. Первая цифра 8 является значащей, так как она отлична от нуля. Соответственно, нам необходимо округлить результат до одного знака после запятой. Согласно правилам, о которых мы говорили выше, результат будет равен 8,4.
Теперь самый сложный случай. Попробуем округлить 47,336. Так как все цифры отличны от нуля, мы будем округлять результат до целого числа. По математическим правилам он будет равен 47. Если мы имеем дело с трёхзначным числом, необходимо округлить результат до двух знаков, после чего умножить на 10 в нужной степени. Пример: округляем 4289,346 и получаем 43, умноженное на десять в квадрате.
Именно для того и нужна метрология, чтобы правильно округлять и записывать результат в технической документации. А также для избежания ошибок при ведении расчетов в разработке технических устройств.
Заключение
Теперь вы знаете, как правильно округлять и сможете делать все необходимые расчеты самостоятельно. Главное, доходы округлять в меньшую сторону, а расходы — в большую. И тогда вам точно будет хватать денег на все покупки, и останется небольшая сумма, которую можно потратить на развлечения. Успехов вам!
Видео
В нашем видео подробно рассказано о правилах округления чисел — с примерами.
Округление чисел
Приближённые значения
Иногда в вычисления нет необходимости использовать точные числовые значения. Для ускорения или упрощения расчётов очень часто достаточно получения приближенного результата. Для этого производят округления чисел, которые участвуют в расчетах а также и конечный результат вычислений. Приближённые значения используют тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета.
Например можно сказать, что дорога до дома занимает полчаса. Это прибличительное значение, поскольку точно сказать сколько времени займет путь до дома или слишком сложно или в большинстве случаев не так важно. Главное обозначить порядок чисел и этого бывает вполне достаточно.
В математике приближенные значения указываются с помощью специального знака.
Чтобы указать приблизительное значение чего-либо, используют округление чисел.
Округление чисел
Суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Первое правило округления:
Второе правило округления:
Третье правило округления:
Как округлить число до целого
Правило округления числа до целого
Чтобы округлить число до целого (или округлить число до единиц), надо отбросить запятую и все числа, стоящие после запятой.
Примеры округления числа до целого:
\[ 86,\underline 2 4 \approx 86 \]
Чтобы округлить число до целого, отбрасываем запятую и все стоящие после нее числа. Так как первая отброшенная цифра 2, предыдущую цифру не изменяем. Читают: «восемьдесят шесть целых двадцать четыре сотых приближенно равно восьмидесяти шести целым».
\[ 274,\underline 8 39 \approx 275 \]
Округляя число до целого, отбрасываем запятую и все следующие за ней цифры. Так как первая из отброшенных цифр равна 8, предыдущую увеличиваем на единицу. Читают: «Двести семьдесят четыре целых восемьсот тридцать девять тысячных приближенно равно двести семидесяти пяти целым».
\[ 0,\underline 5 2 \approx 1 \]
При округлении числа до целого запятую и все стоящие за ней цифры отбрасываем. Поскольку первая из отброшенных цифр — 5, предыдущую увеличиваем на единицу. Читают: «Нуль целых пятьдесят две сотых приближенно равно одной целой».
\[ 0,\underline 3 97 \approx 0 \]
Запятую и все стоящие после нее цифры отбрасываем. Первая из отброшенных цифр — 3, поэтому предыдущую цифру не изменяем. Читают: «Нуль целых триста девяносто семь тысячных приближенно равно нуль целых».
\[ 39,\underline 7 04 \approx 40 \]
Первая из отброшенных цифр — 7, значит, стоящую перед ней цифру увеличиваем на единицу. Читают: «Тридцать девять целых семьсот четыре тысячных приближенно равно сорока целым». И еще пара примеров на округление числа до целых:
Как округлить до десятых
Правило округления числа до десятых.
Чтобы округлить десятичную дробь до десятых, надо оставить после запятой только одну цифру, а все остальные следующие за ней цифры отбросить.
Примеры округления до десятых числа:
\[ 23,7\underline 5 \approx 23,8 \]
Чтобы округлить число до десятых, оставляем после запятой первую цифру, а остальное отбрасываем. Так как первая отброшенная цифра 5, то предыдущую цифру увеличиваем на единицу. Читают: «Двадцать три целых семьдесят пять сотых приближенно равно двадцать три целых восемь десятых».
\[ 348,3\underline 1 \approx 348,3 \]
Чтобы округлить до десятых данное число, оставляем после запятой лишь первую цифру, остальное — отбрасываем. Первая отброшенная цифра 1, поэтому предыдущую цифру не изменяем. Читают: «Триста сорок восемь целых тридцать одна сотая приближенно равно триста сорок одна целая три десятых».
\[ 49,9\underline 6 2 \approx 50,0 \]
Округляя до десятых, оставляем после запятой одну цифру, а остальные — отбрасываем. Первая из отброшенных цифр — 6, значит, предыдущую увеличиваем на единицу. Читают: «Сорок девять целых, девятьсот шестьдесят две тысячных приближенно равно пятьдесят целых, нуль десятых».
\[ 7,0\underline 2 8 \approx 7,0 \]
Округляем до десятых, поэтому после запятой оставляем только первую из цифр, остальные — отбрасываем. Первая из отброшенных цифр — 4, значит предыдущую цифру оставляем без изменений. Читают: «Семь целых двадцать восемь тысячных приближенно равно семь целых нуль десятых».
\[ 56,8\underline 7 06 \approx 56,9 \]
Чтобы округлить до десятых данное число, после запятой оставляет одну цифру, а все следующие за ней — отбрасываем. Так как первая отброшенная цифра — 7, следовательно, к предыдущей прибавляем единицу. Читают: «Пятьдесят шесть целых восемь тысяч семьсот шесть десятитысячных приближенно равно пятьдесят шесть целых, девять десятых».
Как округлить число до сотых
Правило округления числа до сотых
Чтобы округлить число до сотых, надо оставить после запятой две цифры, а остальные отбросить.
Пример округления числа до сотых:
\[ 32,78\underline 6 \approx 32,79 \]
Чтобы округлить число до сотых, оставляем после запятой две цифры, а следующую за ними цифру отбрасываем. Поскольку эта цифра — 9, предыдущую цифру увеличиваем на единицу. Читают: «Тридцать две целых семьсот восемьдесят шесть тысячных приближенно равно тридцать две целых семьдесят девять сотых».
\[ 6,96\underline 1 \approx 6,96 \]
Округляя данное число до сотых, оставляем после запятой две цифры, а третью — отбрасываем. Так как отброшенная цифра — 1, предыдущую цифру оставляем без изменений. Читают: «Шесть целых девятьсот шестьдесят одна тысячная приближенно равно шесть целых девяносто шесть сотых».
\[ 17,48\underline 3 9 \approx 17,48 \]
При округлении до сотых оставляем после запятой две цифры, остальные — отбрасываем. Первая из отброшенных цифр — 3, поэтому предыдущую цифру не изменяем. Читают: «Семнадцать целых четыре тысячи тридцать девять десятитысячных приближенно равно семнадцать целых сорок восемь сотых».
\[ 0,12\underline 5 4 \approx 0,13 \]
Чтобы округлить данное число до сотых, после запятой оставим лишь две цифры, а остальные — отбросим. Первая из отброшенных цифр равна 5, поэтому предыдущую цифру увеличиваем на единицу. Читают: «Нуль целых тысяча двести пятьдесят четыре тысячных приближенно равно нуль целых тринадцать сотых».
\[ 549,30\underline 7 3 \approx 549,31 \]
При округлении числа до сотых оставляем после запятой две цифры, остальные — отбрасываем. Поскольку первая из отброшенных цифр — 7, предыдущую цифру увеличиваем на единицу. Читаем: «Пятьсот сорок девять целых, три тысячи семьдесят три десятитысячных приближенно равно пятьсот сорок девять целых, тридцать одна сотая».
Как округлить число до тысячных
Правило округления числа до тысячных
Чтобы округлить десятичную дробь до тысячных, надо оставить после запятой только три цифры, а остальные следующие за ней цифры отбросить.
Пример кругления числа до тысячных:
\[ 3,785\underline 4 \approx 3,785 \]
Чтобы округлить число до тысячных, после запятой нужно оставить лишь три цифры, а четвертую — отбросить. Поскольку отброшенная цифра — 4, предыдущую цифру оставляем без изменений. Читают: «Три целых, семь тысяч восемьсот пятьдесят четыре десятитысячных приближенно равно три целых, семьсот восемьдесят пять тысячных».
\[ 37,207\underline 6 \approx 37,208 \]
Чтобы округлить это число до тысячных, после запятой оставляем три цифры, а четвертую — отбрасываем. Отброшенная цифра — 6, значит предыдущую цифру увеличиваем на единицу. Читают: «Тридцать семь целых две тысячи семьдесят шесть десятитысячных приближенно равно тридцать семь целых двести восемь тысячных».
\[ 69,999\underline 8 1 \approx 70,000 \]
Округляя число до тысячных, оставляем после запятой три цифры, а все остальные — отбрасываем. Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».
\[ 863,124\underline 2 3 \approx 863,124 \]
Округляем число до тысячных, поэтому после запятой оставляем первые три цифры, а следующие за ними — отбрасываем. Так как первая из отброшенных цифр — 2, то предыдущую цифру не меняем. Читают: «Восемьсот шестьдесят три целых двенадцать тысяч четыреста двадцать три стотысячных приближенно равно восемьсот шестьдесят три целых сто двадцать четыре тысячных».
\[ 0,003\underline 5 9 \approx 0,004 \]
Чтобы округлить данное число до тысячных, первые три цифры, стоящие после запятой, оставляем, а все остальные — отбрасываем. Первая из отброшенных цифр равна 5, а это означает, что предыдущую цифру следует увеличить на единицу. Читают: «Нуль целых триста пятьдесят девять стотысячных приближенно равно нуль целых четыре тысячных».
Как округлить число до десятков
Правило округления числа до десятков
Чтобы округлить число до десятков, нужно цифру в разряде единиц заменить нулем, а если в записи числа есть цифры после запятой, то их следует отбросить.
Примеры округления числа до десятков:
\[ 58\underline 3 \approx 580 \]
Чтобы округлить число до десятков, цифру в разряде единиц (то есть последнюю цифру в записи натурального числа) заменяем нулем. Так как эта цифра равна 3, предыдущую цифру не изменяем. Читают: «Пятьсот восемьдесят три приближенно равно пятьсот восемьдесят».
\[ 103\underline 7 \approx 1040 \]
Округляем до десятков, поэтому цифру в разряде единиц заменяем на нуль. Поскольку эта цифра — 7, предыдущую увеличиваем на единицу. Читают: «Тысяча тридцать семь приближенно равно тысяча сорок».
Как округлить число до сотен
Правило округления числа до сотен
Чтобы округлить число до сотен, надо цифры в разряде единиц и десятков заменить нулями. При округлении до сотен десятичной дроби запятую и все стоящие после нее цифры отбрасывают.
Примеры округления числа до сотен:
\[ 23\underline 1 7 \approx 2300 \]
Чтобы округлить до сотен это число, цифры в разряде единиц и десятков (то есть две последние цифры в записи) заменяем нулями. Так как первая из замененных на нуль цифр равна 1, предыдущую цифру не изменяем. Читают: «Две тысячи триста семнадцать приближенно равно две тысячи триста».
\[ 45\underline 8 1 \approx 4600 \]
Округляя данное число до сотен, две последние цифры в его записи заменяем на нули. Поскольку первая из замененных нулем цифр равна 8, предыдущую цифру увеличиваем на единицу. Читают: «Четыре тысячи пятьсот восемьдесят один приближенно равно четыре тысячи шестьсот».
\[ 785\underline 0 9 \approx 78500 \]
Округляем число до сотен, значит две последние цифры в записи числа — десятки и единицы — заменяем нулями. Первая из замененных нулем цифр равна нулю, поэтому предыдущую переписываем без изменений. Читают: «Семьдесят восемь тысяч пятьсот девять приближенно равно семьдесят восемь тысяч пятьсот».
\[ 939\underline 5 2 \approx 94000 \]
Чтобы округлить до сотен данное число, в разрядах десятков и единиц цифры заменяем на нули. Так как первая из замененных на нуль цифр — 9, предыдущую увеличиваем на единицу. Читают: «Девяносто три тысячи девятьсот пятьдесят два приближенно равно девяносто четыре тысячи».
\[ 14\underline 7 3,12 \approx 1500 \]
Чтобы округлить до сотен десятичную дробь, запятую и все стоящие после запятой цифры необходимо отбросить, а две последние цифры целой части (единицы и десятки) — заменить нулями. Первая из замененных на нуль цифр равна 7, поэтому к предыдущей цифре прибавляем единицу. Читают: «Тысяча четыреста семьдесят три целых двенадцать сотых приближенно равно тысяча пятьсот».
Как округлить число до тысяч
Правило округления числа до тысяч
Чтобы округлить число до тысяч, надо цифры в разрядах сотен, десятков и единиц заменить нулями. При округлении до тысяч десятичной дроби запятую и все стоящие после нее цифры нужно отбросить.
Примеры округления числа до тысяч :
\[ 82\underline 3 71 \approx 82000 \]
Чтобы округлить до тысяч это число, надо цифры в разрядах сотен, десятков и единиц заменить нулями (у тысяч три нуля в конце записи, столько же нулей в конце числа должно получиться и при округлении до тысяч). Так как первая из цифр, которую мы заменили на нуль, равна 3, то предыдущую цифру оставляем без изменений. Читают: «Восемьдесят две тысячи триста семьдесят один приближенно равно восемьдесят две тысячи».
\[ 40\underline 6 28 \approx 41000 \]
При округлении до тысяч три последних цифры — в разрядах сотен, десятков и единиц — заменяем на нули. Так как первая из замененных нулем цифр равна 6, предыдущую цифру увеличиваем на единицу. Читают: «Сорок тысяч шестьсот двадцать восемь приближенно равно сорок одна тысяча».
\[ 159\underline 7 32 \approx 160000 \]
Округляя до тысяч данное число, цифры в разрядах сотен, десятков и единиц заменяем нулями. Первая из замененных нулем цифр равна 7, поэтому к предыдущей цифре прибавляем единицу. Читают: «Сто пятьдесят девять тысяч семьсот тридцать два приближенно равно сто шестьдесят тысяч».
\[ 238\underline 1 97 \approx 238000 \]
Округляем число до тысяч, поэтому цифры в разрядах сотен, десятков и единиц заменяем на нули. Так как первая из цифр, которую мы заменили нулем, равна 1, то предыдущую цифру переписываем без изменений. Читают: «Двести тридцать восемь тысяч сто девяносто семь приближенно равно двести тридцать восемь тысяч».
\[ 457\underline 2 49,83 \approx 457000 \]
Чтобы округлить десятичную дробь до тысяч, запятую и все цифры после запятой отбрасываем, а цифры в разрядах сотен, десятков и единиц заменяем нулями. Так как первая из замененных нулем цифр — 2, то предыдущую цифру не изменяем. Читают: «Четыреста пятьдесят семь тысяч двести сорок девять целых, восемьдесят три сотых приближенно равно четыреста пятьдесят тысяч».