Что понимают под живым сечением потока

Гидравлические элементы живого сечения. Уравнение расхода

При изучении потоков жидкостей вводят ряд понятий, характеризующих потоки с гидравлической и геометрической точек зрения: площадь живого сечения, периметр смачивания, гидравлический радиус.

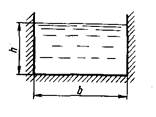
Площадью живого сечения, или живым сечением потока, называют площадь сечения потока, расположенную перпендикулярно направлению движения жидкости, т. е. скорость движения элементарных струек направлена перпендикулярно сечению потока. Площадь живого сечения обозначается через ω (в м 2 ).

В реальных условиях поверхности живых сечений являются криволинейными, для расчетов в целях упрощения принимают живые сечения плоскими. В практике под живым сечением понимается поперечное сечение канала, канавы, трубы. Форма живого сечения бывает в виде трапеции, треугольника, прямоугольника.

Живое сечение может быть ограничено твердыми стенками полностью или частично, например, водопропускные трубы, боковые водоотводные канавы, нагорные канавы. Условия движения потока жидкости зависят от глубины и ширины живого сечения: если стенки ограничивают поток полностью, движение жидкости осуществляется в напорном режиме, в случае частичного ограничения режима движения режим движения безнапорный.

Смоченным периметром А. называется линия, по которой поток в поперечном сечении соприкасается с твердыми стенками русла.

Рисунок 6.5 Схема к определению периметра смачивания

Для случая напорного движения смоченный периметр в круглой трубе совпадает с его геометрическим периметром и будет равен

Так, для бетонного канала, изображенного на рис. 6.5, периметр смачивания

Гидравлическим радиусом называется отношение площади живого сечения потока к смоченному периметру, т. е.

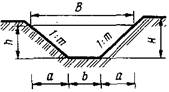
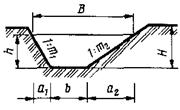
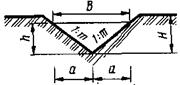
Основные размеры поперечного сечения канав, лотков в зависимости от геометрической формы определяются по схемам, приведенным в табл. 6.1.

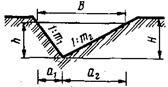
Таблица 6.1 Геометрическая форма поперечного сечения

Геометрическая форма поперечного сечения	Площадь живого сечения, ω	Смоченный периметр, λ	Ширина свободной поверхности, В	Заложение откоса

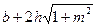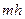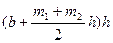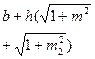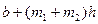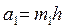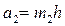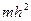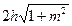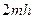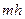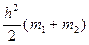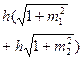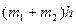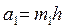Расход потока и его средняя скорость в гидродинамике являются важными характеристиками.

Расходом потока называют количество жидкости, протекающей через данное сечение потока в единицу времени.

В дорожном строительстве приходится иметь дело главным образом с объемным расходом жидкости. Расход жидкости равен произведению средней скорости течения в поперечном сечении на его площадь, т. е.

Если рассматривать поток жидкости как совокупность большого числа элементарных струек, то общий расход жидкости Q для всего потока в целом можно определить как сумму элементарных расходов. Скорости движения этих элементарных струек жидкости в различных точках разные. Законы распределения скоростей будут неодинаковы, с приближением к берегам скорости уменьшаются. Поэтому делают предположение, что частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью, которая называется средней скоростью. Средняя скорость в рассматриваемом сечении условно придается всем частицам жидкости, при этом расход потока соответствует действительному расходу.

Источник

Что понимают под живым сечением потока

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

если угол в радианах, или

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Выражение, стоящее перед , является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Источник

Тока, трубка тока, струйка, живое сечение.

Для упрощения изучения течений в гидромеханике широко используется идеальная жидкость. Происходящие явления сначала исследуются применительно к идеальной жидкости, а затем полученные закономерности переносятся с введением корректирующих поправок на потоки реальных жидкостей.

Течение жидкости может быть установившимся и неустановившимся. При установившемся течении все физические параметры в данной точке потока (скорость, давление и др.) остаются неизменными во времени. Примером установившегося течения может служитьистечение через отверстие в дне сосуда, в котором поддерживается постоянный уровень жидкости. При неустановившемся течении физические параметры в данной точке потока (или некоторые из них) меняются во времени. Для примера можно привести рассматриваемое выше истечение,но безподдержания постоянного уровня жидкости в сосуде, т. е. истечение до полного опорожнения.

Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорными—течения со свободной поверхностью.«Линия тока».—условная линия в потоке жидкости, проведенная так, что вектор скорости

в любой ее точке направлен по касательной (линия 1 на рис.1).Приустановившемся течении линия тока совпадает с траекторией движения частицы жидкости, в любой точке потока существует только одна (неизменная во времени) скорость. Поэтому через данную точку может проходить только одна линия тока, линии тока при установившемся течении

не могут пересекаться.

Если в движущейся жидкости взять бесконечно малый замкнутый контур 2(рис. 1) и через все его точки провести линии тока 3(рис. 1), то образуется трубчатая поверхность, называемая трубкой тока.Часть потока внутри трубки тока называетсяэлементарной струйкой.Струйкужидкости бесконечно малой толщины принято называть элементарной струйкой.

Живое сеченые или просто сечение потока–это поверхность в пределах потока,проведеннаяпо нормали к линиям тока. Как правило,рассматривают плоские живые сечения.Живое сечениекроме своей площади характеризуется смоченным периметром и гидравлическим радиусом.

Смоченный периметр χ(м)—это линия,по которой живое сечение соприкасается сограничивающими его стенками.

Гидравлический радиус R -это отношение пощадиFживого сечения к смоченномупериметру:

2. Расход. Средняя скорость. Уравнение расхода.

Расход —это количество жидкости,которое протекает через данное сечение в единицувремени. Количество жидкости можно измерять в единицах объема,массы или веса.Поэтому различают объемный Q (м 3 /с), массовый Q_m (кг/с) и весовой Q_G (Н/с) расходы. Между этимирасходами существует такая же связь, как между объемом, массой и весом, т.е.

При расчете гидравлических систем наибольшее распространение получил объемный расход Q. Очевидно, что расход связан со скоростью движения жидкости.. В иде-альной жидкости (рис.2, а) отсутствует вязкость, следовательно, нет трения между слоями движущейся жидкости. Поэтому в сечении 1—1струйки идеальной жидкости все скорости одинаковы и эпюра скоростей на рис. 2, а

имеет прямоугольную форму.

Объемный расход идеальной жидкости составит

При течении потока реальной жидкости между ее слоями возникает трение. Крайние слои жидкости из-за трения о стенку имеют практически нулевую скорость (рис.2, б). По мере удаления от стенки каждый последующий слой приобретает более высокую скорость,имаксимальная скорость в сечении v_max отмечается в середине потока. Следовательно, происходит перераспределение скоростей по сечению площадью S, что затрудняет определение математической взаимозависимости между основными геометрическими и кинематическими параметрами потока реальной жидкости.

Поэтому вводится понятие средней скорости в сеченииv_cp, под которой будем понимать скорость, удовлетворяющую следующему равенству:

v_cp — это условная скорость, существующая в каком-то промежуточном слое потока реальной жидкости. Обычно она меньше максимальной скорости v_maxи лежит в пределах0,5v_max

связывающую основные геометрические и кинематические параметры потока в этих сечениях.

Это уравнение получило название уравнения неразрывности,илиуравнения расхода. Оно позволяет определить среднюю скорость в любомсечении потока жидкости (например, v_cpl), если известны хотя бы одна из средних скоростей этого потока (например, v_cp2) и его геометрические размеры. Уравнение является законом сохранения вещества для потока (или

струйки) жидкости,записанное при условии постоянства плотности жидкости в пределах рассматриваемого потока.

При расчетах машиностроительных гидросистем говорят о скорости в сечении потока, при этом понимают ее среднюю величину.

3. Ламинарный и турбулентный режим движения жидкости.

При ламинарном режиме жидкость движется отдельными струями без их перемешивания, все линии тока определяются формой русла потока и, если оно является прямолинейным с постоянным сечением, линии тока параллельны стенкам. В ламинарном потоке отсутствуют видимые вихреобразования, но существуют бесконечно малые (точечные) вихри вокруг мгновенных центров вращения частиц жидкости.

Если скорость течения жидкости начнет возрастать и при каком-то ее значении ламинарная

струйка начнет разрушаться . Такую скорость принято называть критической (v_кр). Разрушение струйки сопровождается завихрениями и перемешиванием ее с соседними слоями воды. Такой режим течения принято называть турбулентным.

Источник

Гидравлические элементы потока, расход, средняя скорость. Уравнение неразрывности (сплошности) потока.

В качестве основных элементов, характеризующих поток жидкости, различают: площадь живого сечения, смоченный периметр, гидравлический радиус, эквивалентный диаметр, средняя скорость потока, расход жидкости.

Живым сечением называется сечение потока, проведенное перпендикулярно линиям тока. (Линией тока называется такая линия, касательные к которой в любой точке, совпадают с направлением векторов скорости частиц в данный момент времени.)

Смоченный периметр – часть периметра живого сечения потока, в которой жидкость соприкасается с твердыми стенками канала или трубы. (χ, м).

Гидравлический радиус – характеристика живого сечения, представляющая собой отношение площади живого сечения к смоченному периметру

R=w/ χ

Средняя скорость – фиктивная скорость (v, м/с), с которой должны двигаться все частицы жидкости в данном живом сечении, чтобы расход, проходящий через него, был равен расходу, вычисленному по действительным скоростям всех частиц в этом же сечении. v=Q/w

Расход– количество жидкости, протекающей через живое сечение потока в единицу времени.

расход жидкости по тока равен произведению площади его живого сечения на среднюю скорость(Q=v * w). При движении жидкости различают, соответственно расходы: объемный, весовой и массовый.

u1 w1=u2 w2=……=un wn=const

Это уравнение называется уравнением неразрывности (сплошности) для элементарной

струйки. Оно показывает, что при установившемся движении элементарный объемный расход несжимаемой жидкости есть величина постоянная вдоль всей струйки.

Учитывая, что поток жидкости представляет собой совокупность большого числа элементарных струек, сплошь заполняющих площадь его живого cечения, общий расход жидкости для всего потока, очевидно, можно определить как сумму

элементарных расходов отдельных струек, из которых состоит

u – скорость элементарных струек

Уравнение Д. Бернулли для элементарной струйки невязкой жидкости.

Члены уравнения Бернулли измеряются в единицах длины и носят следующие название: z — нивелирная высота, или геометрический напор; р/γ — пьезометрическая высота; u 2 /2g —

скоростная высота, или скоростной напор.

Уравнение Д. Бернулли для элементарной струйки реальной жидкости. Геометрическое и энергетическое толкование уравнения Д. Бернулли.

Благодаря вязкости в реальной жидкости происходят потери механической энергии потока на трение внутри жидкости и о стенки канала. При этом происходит рассеивание (диссипация) энергии. Энергия, потерянная на трение, превращается в теплоту и идет на пополнение запаса внутренней энергии жидкости, а часть ее отводится в виде тепла через стенки канала.

Внутренняя энергия жидкости не может быть непосредственно использована для приведения жидкости в движение и поэтому в гидравлике рассматривается как потеря механической энергии (потеря напора).

Для реальной жидкости равенство нарушается, и вместо него имеем , где – потеря напора на участке 1–2. Тогда для элементарной струйки реальной жидкости уравнение Бернулли примет вид

Таким образом, полный напор вдоль струйки реальной жидкости уменьшается. Для характеристики относительного изменения полного напора на единицу длины вводится понятие о гидравлическом уклоне

Например, на участке трубопровода 1–2 (см. рис. 4.26)

где l1-2 – длина участка 1–2.

Таким образом, гидравлическим уклоном называется отношение потери напора к длине, на которой она происходит.

Кроме того, вводится еще понятие о пьезометрическом уклоне

Пьезометрический уклон может быть положительным, равным нулю и отрицательным.

Источник