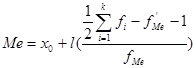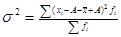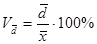Что предполагает вариационное исследование
Тема 5: Вариационный анализ
§1. Вариация признаков и ее причины
§2. Ряды распределения
§3. Структурные характеристики вариационного ряда.
§4. Показатели силы вариации.
§5. Показатели интенсивности вариации
§6. виды дисперсии. Правило сложения дисперсии.
Вариацией значения какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени.
Причина вариации: разные условия существования ЕСС именно вариация порождает необходимость в такой науке как статистика.
Проведение вариационного анализа начинается с построения вариационного ряда – упорядоченное распределение единиц совокупности по возрастающим или по убывающим признакам и подсчет соответствующих частот.
Ранжированный вариационный ряд – перечень отдельных ед. совокупности в порядке возрастания убывания ранжированного признака
| БАНК | Капитал тыс. руб. |
| СБ РФ | 96007237 |
| Внешторгбанк | 47991724 |
Дискретный вариационный ряд – таблица состоящая из 2 х строк – полимерных значений варьирующего признака и кол-во единиц с данным значением признака.
| Кол-во детей в семье | 0 | 1 | 2 | 3 | 4 |
| Кол-во семей | 20 | 40 | 45 | 10 | 5 |
Интервальный вариационный ряд строится в случаях:
2. признака принимает любые значения в определенном диапазоне
При построении интервального вариационного ряда необходимо выбрать оптимальное количество групп, самый распространенный способ по формуле Стерджесса
k – количество интервалов
n – объем совокупности
При расчетах почти всегда получают дробные значения, округления производить до целого числа.
Длина интервала – l
1. нижняя граница последующего интервала повторяет верхнюю границу последующего интервала
2. С индивидуальными границами в интервал входят верхняя и нижняя границы
3. открытый интервал, интервал с одной границей
В случае открытого интервала l принимается равной длине смежного с ним интервала, либо исходя из логических соображений.
| Стаж | До 5 | 5-7 | 7-9 |
| Кол-во рабочих |
При расчетах по интервальному вариационному ряду за xi принимается середина интервала.
 |
Интервалы могут быть как равные так и нет. При изучении вариационного ряда существенную помощь оказывает графическое изображение. Дискретный вариационный ряд изображается с помощью полигона.
Интервальный вариационный ряд изображается с помощью гистограммы.
 |
Накопленная частота
| xi | 0 | 1 | 2 | 3 | 4 |
| fi | 20 | 40 | 45 | 10 | 5 |
Кумулята – распределение меньше чем
 |
Огива – распределение больше чем
Медиана – значение признака делящее всю совокупность на две равные части.
Для дискретного вариационного ряда расчет медианы: если n-четное, то №Ме медианой единицы
Интервальный вариационный ряд:
k – количество интервалов
х0 – нижняя граница медианного интервала
l – длина медианного интервала



Медианный интервал – первый интервал накопленная частота которого превышает половину от общей суммы частот.
| 0-5 | 5-10 |  10-15 10-15 | 15-20 |
| 15 | 20 | 40 | 25 |
Графически медиана находится по кумуляте.
2. Квартили – значение признака делящее совокупность на 4 равные части.
1 ый квартиль
3 ий квартиль
2 ой квартиль – медиана.
xQ 1 xQ3 – нижняя граница интервала содержащего 1 го и 3 го квартили.
l – длина интервала



Для характеристики вариационного ряда используются:
Децили – делят совокупность на 10 равных частей, Перцитили – делят совокупность на 100 равных частей.
3. Мода – часто встречающаяся характеристика признака. Для дискретного вариационного ряда – наибольшая частота. Для интервального вариационного ряда мода рассчитывается по следующей формуле:

l – длина модального интервала
fMo – частота модального интервала
fMo+1 – частота интервала следующего за модальным
Модальный интервал – интервал с наибольшей частотой. Графически мода находится по гистограмме.
1. Размах вариации
2. Среднее линейное отклонение


4. Средне квадратическое отклонение
Свойство дисперсии.
1.
1. уменьшение всех значений признака на одну и ту же величину не меняет величину дисперсии.
2. Уменьшение всех значений признаков в к раз уменьшает величину дисперсии в к 2 раз, а СКО в к раз
3. 




В условиях нормального распределения существует следующая зависимость между 

В пределах 
В пределах 
Для сравнения вариации признаков в разных совокупностях или для сравнения вариации разных признаков в одной совокупности используются относительные показатели, базой служит средняя арифметическая.
1. Относительный размах вариации.
2. Относительное линейное отклонение
3. Коэффициент вариации
данные показатели дают не только сравнительную оценку но и образуют однородность совокупности. Совокупность считается однородной если коэффициент вариации не превышает 33%.
На ряду с изучением вариации признака по всей совокупности в целом, часто бывает необходимо проследить количественные изменения признака, но группам, на которые делится совокупность и между ними. Эта достигается путем вычисления 
1. Общая дисперсия
2. Межгрупповая дисперсия
3. Внутригрупповая дисперсия (остаточная)
1. измеряет вариацию признака во всей совокупности под влиянием все факторов обусловивших данную вариацию
Пример: потребление йогурта: при выборке 100 человек
xi –индивидуальное значение признака


2. характеризует вариацию признака под влиянием признака фактора положенного в основу группировки.



3. 
xij – i значение признака в j группе

fij – частота i-го признака в j группе
Существует правило которое связывает 3 вида дисперсии, оно называется правило сложения дисперсии.


n – общая сумма частот
основная задача анализа вариационных рядов – выявление закономерности распределения частот.
Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду в функционально связанным изменением значения признака.
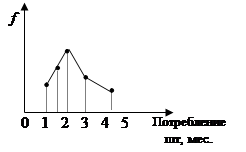 |
Кривую распределения можно построить с помощью полигона и гистограммы. Целесообразно свести эмпирическое распределение к теоретическому, к одному из хорошо изученных виду.
Кривая нормального распределения.
Различают следующие разновидности кривых распределения:
Для однородных совокупностей характерны одновершинные кривые, много вершинная кривая говорит о неоднородности совокупности и необходимости перегруппировки.
Выяснение общего характера распределения предполагает оценку его однородности, и расчет асимметрии и эксцесса. Для симметричных распределений
Для сравнительного изучения асимметрии различных распределений вычисляется коэффициент асимметрии As.



Если 
Если As 0, то As – правосторонняя.
Если 

ТЕМА 6. ВАРИАЦИОННЫЙ АНАЛИЗ
6.1. Сущность и значение изучения вариации признаков
6.2. Абсолютные и относительные показатели вариации
6.3. Свойства вариации и правила сложения дисперсии
6.1. Рассматривая зарегистрированные в процессе статистического наблюдения величины того или иного признака у отдельных единиц совокупности, можно обнаружить между ними различия.
Если индивидуальные значения признака примерно одинаковые, то средняя будет достаточно надёжной показательной характеристикой изучаемой совокупности, если же ряд распределения отличается значительным рассеиванием индивидуальных значений признака, то средняя не будет являться надёжной характеристикой и иметь практическое значение. Одним словом, для каждой единицы совокупности размер изучаемого признака может принимать различные значения, то есть имеет некоторую вариацию.
Вариация признака – наличие различий в численных значениях признаков у отдельных единиц совокупности. Она порождается комплексом условий, действующих на совокупность и её единицы. Именно вариация предопределяет необходимость статистики. Вариацию классифицируют в пространстве и во времени:
— в пространстве – колеблемость значений признака по разным объектам, территориям и т.п.;
— во времени – изменение значений признака в различные периоды или моменты времени.
Наличие вариации ставит перед статистикой задачи: Определение меры вариации и соответствующих измерителей; измерение степени её колеблемости; выявление сущности степени вариации и определяющих её факторов.
По степени вариации оценивают однородность совокупности, устойчивость индивидуальных значений, типичность средней, степень воздействия на данный признак других варьирующих признаков и определяют взаимосвязь между ними. Показатели вариации применяются при оценке ритмичности работы предприятия, контроля и устойчивости производственного процесса, организации выборочного наблюдения, разработке материалов экспертных опросов, переписи и т.д.
В математической части измерения вариации, теория статистика опирается на математическую статистику, применяя при этом показатели, которые классифицируют на абсолютные и относительные.
6.2. Абсолютные – размах вариации, среднее линейное отклонение, дисперсия и середнеквадратическое отклонение. Абсолютные показатели вариации всегда величины именованные. В зависимости от исходных данных их рассчитывают по несгруппированным и сгруппированым значениям.
К недостаткам можно отнести то, что очень большое и очень маленькое значение совокупности может быть обусловлено случайными обстоятельствами и рассматриваться как аномальным, что в целом даёт искажённую амплитуду колебания признака против нормальных её размеров.
Поэтому для анализа вариации необходим показатель, который отражал бы все колебания варьирующего признака, дававший бы обобщённую характеристику. Будет логичным, если в качестве такой величины использовать среднюю, так как в ней будут более или менее погашаться случайные отклонения от закономерного хода развития явления и отражаться типичный размер признака. Следовательно, средняя, должна быть своего рода центра тяжести, вокруг которого происходит колебание, рассеивание индивидуальных значений признака.
Такая средняя является средним линейным отклонением.
Среднее линейное отклонение (d) – средняя арифметическая из отклонений отдельных значений варьирующего признака от средней величины:
Данный показатель даёт обобщённую характеристику степени колеблемости признака в совокупности.
Поскольку сумма отклонений отдельных значений признака от средней равна нулю (одно из свойств средней арифметической), то все отклонения приходится брать по модулю, на что указывают прямые скобки в числителе. В итоге при исчислении допускаются некорректные, с точки зрения математики, действия, что побудило искать иной способ оценки вариации, чтобы иметь дело только с положительными числами.
Дисперсия (σ 2 ) – средний квадрат отклонений индивидуальных значений варьирующего признака от их средней величины:
σ² = ∑(х-хср) 2 / ∑n (простая); σ² = ∑(х-хср) 2 ·ƒ / ∑ƒ (взвешенная)
Однако вследствие суммирования квадратов отклонений дисперсия даёт искажённое представление об отклонениях, измеряя их во второй степени, хотя все варианты изучаемой совокупности и выражены изначально в первой степени. Поэтому их необходимо преобразовать, Для этого достаточно извлечь корень квадратный из дисперсии, В результате получим новую величину, именуемую средним квадратическим отклонением.
Среднеквадратическое отклонение (σ) – наиболее обобщающая характеристика размеров вариации признака в совокупности, главное сущностное измерение меры колеблемости:
σ = √∑(х-хср) 2 / ∑n (простое); σ = √∑(х-хср) 2 ·ƒ / ∑ƒ(взвешенное)
Дисперсия и среднеквадратическое отклонение являются общепринятыми мерами вариации. Используют в статистических исследованиях, технике, биологии, международной практике учёта, разработке СНС.
Для оценки интенсивности вариации, однородности совокупности, сравнения её в различных явлениях используют относительные показатели вариации, являющиеся результатом соотношения полученных абсолютных значений и средней арифметической величины. Выражаются в процентах.
Различают относительные показатели размаха вариации (коэффициент осцилляции), среднего линейного отклонения, коэффициент вариации.
Относительный размах вариации (VR) – отражает относительную меру колеблемости крайних значений признака вокруг средней:
Относительное среднее линейное отклонение (Vd) – отражает долю усреднённого значения абсолютных отклонений от средней величины:
Коэффициент вариации ( Vσ) – наиболее распространённый показатель колеблемости, поскольку среднеквадратическое отклонение даёт наиболее общую характеристику колеблемости всех вариантов совокупности:
Проводится данное изучение вычислением и дальнейшим анализом различных видов дисперсий.
Различают общую дисперсию, межгрупповую и внунтригрупповую.
Общая дисперсия (σо 2 ) – измеряет вариацию признака всей совокупности под воздействием всех факторов, обусловивших данную вариацию. Рассчитывается по простой и взвешенной формулам.
σi 2 = Σ(хi-хo) 2 n / Σn(простая); σi 2 = Σ(хi-хo) 2 f / Σf(взвешенная)
Межгрупповая дисперсия (δх 2 ) – характеризует вариацию признака, возникающую под воздействием какого-либо одного фактора, стоящего в основании группировки. Данная характеристика проявляется в отклонении групповых средних от общей средней.
δх 2 = Σ(хi-хо) 2 n/Σn
Внутригрупповая дисперсия (σi 2 ) – показывает случайную вариацию, её какую –то часть, происходящую под влиянием случайных, неучтённых факторов. Не зависит от изучаемого фактора, стоящего в основании группировки.
σi 2 = Σ(х-хi) 2 n / Σn(простая); σi 2 = Σ(х-хi) 2 f / Σf(взвешенная)
Средняя из внутригрупповых дисперсий исчисляется по формуле:
Эта средняя также отражает ту часть вариации, обусловленную действием всех прочих неучтённых факторов, кроме фактора, по которому осуществилась группировка (группировочный).
6.3. По полученным величинам всех дисперсий в статистике изучается правило сложения дисперсий, согласно которому общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий: σо 2 = δх 2 + σi 2
Таким образом, по полученным величинам дисперсий, согласно ему, можно рассчитать влияние изучаемых признаков на результативный фактор. При этом необходимо знать: если групповые средние будут равны между собой и совпадут с общей средней, т.е. межгрупповая средняя равна нулю, то в данном случае факторный признак не оказывает влияния на результативный.
В статистическом анализе широко используется эмпирический коэффициент детерминации (η 2 = δх 2 /σi 2 ), показывающий удельный вес общей вариации изучаемого признака, обусловленной вариацией группировочного признака, а также эмпирическое корреляционное отношение (η) – как результата извлечения корня квадратного из первого. Эмпирическое корреляционное отношение характеризует влияние признака, лежащего в основании группировки на вариацию результативного. Измеряется в пределах от 0 до 1.