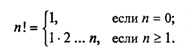Что предшествует разработке алгоритма

Основные этапы полного построения алгоритма

· проверка правильности алгоритма;

· анализ алгоритма и его сложности;

· написание программы на подходящем языке;

Постановка задачи

Прежде чем понять задачу, следует её точно сформулировать. Это условие само по себе не является достаточным для понимания задачи, но оно абсолютно необходимо. Для плохо сформулированных задач полезны следующие вопросы:

· Понятна ли терминология, используемая в предварительной формулировке?

· Что дано? Что нужно найти? В чём состоит условие?

· Каких данных не хватает? Все ли они нужны?

· Являются ли какие-то имеющиеся данные бесполезными?

· Какие сделаны допущения?

Возможны и другие вопросы в зависимости от конкретной задачи. Часто после получения полных или частичных ответов на некоторые из вопросов их приходится ставить повторно.

Построение модели

Задача чётко поставлена, теперь нужно сформулировать для неё математическую модель. Это очень важный шаг в процессе решения, и его надо хорошо обдумать. Выбор модели существенно влияет на остальные этапы процесса решения.

Ясно, что невозможно предложить набор правил, автоматизирующих стадию моделирования. Большинство задач должно рассматриваться индивидуально. Тем не менее существует несколько полезных руководящих принципов. Выбор модели – в большей степени дело искусства, чем науки, и, вероятно, эта тенденция сохранится. Изучение удачных моделей – это наилучший способ приобрести опыт в моделировании.

Приступая к разработке модели, следует задать, по крайней мере, два основных вопроса:

· Какие математические структуры больше всего подходят для задачи?

· Существует ли решение аналогичной задачи?

Второй вопрос, возможно, самый полезный во всей математике. В контексте моделирования он часто даёт ответ на первый вопрос. Действительно, большинство решаемых в математике задач, как правило, являются модификациями уже решённых. Поскольку большинство из нас не обладает талантами великих математиков, то для продвижения вперёд приходится руководствоваться накопленным опытом.

Сначала нужно рассмотреть первый вопрос. Необходимо описать математически, что знаем, и что хотим найти. На выбор соответствующей структуры оказывают влияние следующие факторы: 1) ограниченность наших знаний относительно небольшим количеством структур; 2) удобство представления; 3) простота вычислений; 4) полезность различных операций, связанных с рассматриваемой структурой или структурами.

Сделав пробный выбор математической структуры, задачу следует переформулировать в терминах соответствующих математических объектов. Это будет одна из возможных моделей, если можно утвердительно ответить на такие вопросы:

· Вся ли важная информация задачи хорошо описана математическими объектами?

· Существует ли математическая величина, ассоциируемая с искомым результатом?

· Выявлены ли какие-нибудь полезные отношения между объектами модели?

· Можно ли работать с моделью? Удобно ли с ней работать?

Разработка алгоритма

Как только задача чётко поставлена и для неё построена модель, следует приступить к разработке алгоритма её решения. Выбор метода разработки, зачастую сильно зависящий от выбора моделей, может в значительной степени повлиять на эффективность алгоритма решения. Два разных алгоритма могут быть правильными, но очень сильно отличаться по эффективности.

Многие программисты затрачивают относительно небольшое время на стадию разработки алгоритма при создании программ – проявляется желание как можно быстрее начать писать саму программу. Однако этому побуждению не стоит поддаваться! На стадии разработки требуется тщательное обдумывание; нужно также уделить внимание двум предшествующим и первым трём следующим за стадией разработки этапам. Как и следует ожидать, все восемь перечисленных этапов являются взаимосвязанными. В особенности первые три сильно влияют на последующие, а шестой и седьмой этапы обеспечивают ценную обратную связь, которая может заставить нас пересмотреть некоторые из предшествующих этапов.

Правильность алгоритма

Доказательство правильности алгоритма – это один из наиболее трудных, а иногда и особенно утомительных этапов создания алгоритма.

Вероятно, наиболее распространенная процедура доказательства правильности программы – это прогон её на разных тестах. Если выданные программой ответы могут быть подтверждены известными или вычисленными вручную данными, возникает искушение сделать вывод, что программа «работает». Однако этот метод редко исключает все сомнения; может существовать случай, когда программа не сработает.

Можно предложить следующую методику доказательства правильности алгоритма [2]. Предположим, что алгоритм описан в виде последовательности шагов, например, от шага 0 до шага m. Постараемся предложить некое обоснование правомерности для каждого шага. В частности, может потребоваться лемма об условиях, действующих до и после пройденного шага. Затем постараемся предложить доказательство конечности алгоритма, при этом будут проверены все подходящие входные данные и получены все подходящие выходные данные. Подобный метод доказательства известен как «доказательство исчерпыванием»; это самый грубый из всех методов доказательства.

Подчеркнём тот факт, что правильность алгоритма ещё ничего не говорит о его эффективности. Исчерпывающие алгоритмы редко бывают хорошими во всех отношениях.

Реализация алгоритма

Как только алгоритм выражен, допустим, в виде последовательности шагов и есть уверенность, что он правильный, настаёт черёд реализации алгоритма, т. е. написание программы для ЭВМ.

Этот существенный шаг может быть довольно трудным. Во-первых, трудность заключается в том, что очень часто отдельно взятый шаг алгоритма может быть выражен в форме, которую трудно перевести непосредственно в конструкции языка программирования (например, для реализации данного шага потребуется целая подпрограмма). Во-вторых, реализация может оказаться трудным процессом потому, что перед тем, как начать писать программу, нужно построить целую систему структур данных для представления важных аспектов используемой модели. Чтобы сделать это, необходимо ответить, например, на такие вопросы:

· Каковы основные переменные? Каких они типов?

· Сколько нужно массивов и какой размерности?

· Имеет ли смысл пользоваться связанными списками?

· Какие нужны подпрограммы (возможно, уже записанные в памяти)?

· Каким языком программирования пользоваться?

Конкретная реализация может существенно влиять на требования к памяти и на скорость алгоритма.

Другой аспект построения программной реализации – это программирование “сверху–вниз”, которое состоит в преобразовании алгоритма в такую последовательность всё более конкретизированных алгоритмов, что окончательный вариант представляет собой программу для ЭВМ.

Сделаем одно важное замечание. Одно дело – доказать правильность конкретного алгоритма, описанного в словесной форме, другое – доказать, что данная программа, предположительно являющаяся реализацией этого алгоритма, также правильна. Таким образом, необходимо очень тщательно следить, чтобы процесс преобразования правильного алгоритма (в словесной форме) в машинную программу «заслуживал доверия».

Источник

Начало разработки алгоритма

В основе разработки алгоритма исходной задачи лежит следующая аксиома.

При невыполнении любого из этих требований алгоритм решения задачи построить невозможно.

Алгоритм решения задачи

Одним из основных алгоритмов является алгоритм решения задачи. В настоящее время существует множество всевозможных его вариантов. Авторы предлагают следующий алгоритм решения (любой решаемой) задачи, запишем его в виде сценария с детализацией:

Начало алгоритма

Составление документации (если есть необходимость).

Рассмотрим в качестве примера постановки задачи следующую задачу.

Задача.
Имеется шляпа, галоши, трансформатор, секундомер. Определить высоту здания.

Шляпа, галоши, трансформатор, секундомер – наличие этих предметов подсказывает о возможности решения данной задачи с точки зрения физики, точнее исследуя движение тела в поле тяготения. В этом случае важнейшей характеристикой предмета для нас будет парусность предмета, с которой связана сила сопротивления воздуха, а, следовательно, точность определения высоты здания.

Для определения высоты данного здания можно предложить следующий эксперимент: определить время свободного падения предмета с нулевой начальной скоростью. В качестве предмета необходимо использовать трансформатор, имеющий наименьшую парусность на единицу массы из всех предложенных предметов (секундомер не в счет, так как ему хватит одного падения, чтобы он перестал работать). По полученному времени, используя закон всемирного тяготения, определить высоту здания.

С крыши здания свободно падает трансформатор. Время его падения определяем секундомером. Используя закономерности свободного падения тела в гравитационном поле, определить высоту здания.

Формулировка данной задачи существенно отличается от формулировки исходной, но с ее помощью мы сможем решить исходную задачу.

Далее для формализованной задачи можно разрабатывать алгоритм решения.

Рассмотренный алгоритм – это первое приближение решения исходной задачи. Здесь важно понять, что для решения поставленной задачи необходима детальная проработка первого шага алгоритма, то есть постановки задачи. По исходной задаче необходимо получить формализованную задачу, которая и будет решаться.

Рассмотрим возможности построения алгоритма формализованной задачи.

Принцип нисходящего проектирования алгоритма

Для дальнейшей разработки решения задачи можно воспользоваться основным инструментом построения алгоритма – это принципом нисходящего проектирования алгоритма.

Принцип нисходящего проектирования алгоритма состоит в иерархически – последовательной разработке алгоритма от сложного к простому. Схематически стандартно предлагается следующее.

И объясняется, что данная задача разбивается на несколько подзадач, каждая из которых решает свою часть поставленной задачи. Это первый уровень детализации поставленной задачи. При необходимости одну или несколько подзадач первого уровня детализации разбивают (каждую) на несколько подзадач, образуя второй уровень детализации и т.д. Принцип нисходящего проектирования алгоритма реализуется, как принцип декомпозиции структур. Все это можно найти в любом учебнике по началам алгоритмики и программирования.

Основным следствием принципа нисходящего проектирования алгоритма (по мнению авторов) является следующее утверждение, относящееся к самому первому уровню детализации алгоритма:

Таким образом, алгоритм любой решаемой задачи можно на первом уровне детализации представить в виде алгоритма, состоящего из трех вспомогательных алгоритмов:

Подобное разбиение мы видим при решении задач физики, математики, химии и т. д. (дано…решение [в буквенном виде…числовое решение]…ответ) названия разные – суть одна.

Это определяется тем, что исходные данные вводятся извне. Данным исполнителем проводится обработка информации. Результат обработки выводится на внешние носители информации. Наиболее четко это видно на вычислительных задачах.

Таким образом, самый верхний уровень необходимо рассматривать как один неделимый блок – формулировка исходной (формализованной) задачи. Далее самый первый уровень детализации необходимо представляется тремя подзадачами. Назовем это ТРИЕДИНОЙ ЗАДАЧЕЙ АЛГОРИТМИКИ. Она едина потому, что каждая из подзадач отдельно от остальных не имеет смысла. И это три задачи, так как каждая из них достаточно замкнута, имеет свои особенности и, поэтому, может разрабатываться отдельно от остальных. А так как задач ВводаИнформации и ВыводаРезультатов ограниченное количество и они решаются отдельно, то далее принцип нисходящего проектирования алгоритма применяется только к задаче ОбработкиИнформации.

Триединая задача алгоритмики

Сформулируем понятие триединой задачи алгоритмики в следующем определении.

Каждую из этих задач можно рассматривать в данном алгоритме как вспомогательный алгоритм. В приложениях №№ 1, 2 (Приложение 1, Приложение 2) рассмотрены задачи Ввода/Вывода для простой переменной. Важно отметить, что разработку алгоритма любой решаемой задачи не только можно, а чаще и необходимо, начинать с триединой задачи алгоритмики.

В дальнейшем геометрическое представление триединой задачи удобно делать в виде:

Над стрелкой задаются имена переменных и их типы, под стрелкой ограничения на эти переменные в заданной задаче; как уже говорилось, стрелки суть входной и выходной потоки, прямоугольник – блок обработки информации.

Важно уяснить, что триединая задача алгоритмики есть не что иное, как алгоритм решения задачи на первом уровне. Действительно, в виде сценария этот алгоритм можно представить в виде:

Для самостоятельной работы ученикам можно предложить любые (по сложности), но формализованные задачи. Основное задание – сформулировать триединую задачу для исходной задачи, то есть выделить и сформулировать задачи: ввода информации, вывода результатов и сформулировать задачу обработки информации. В Приложении 3 приведен пример решения подобных задач.

Обобщая изложенное, можно утверждать, что…

В основе разработки алгоритма исходной задачи лежит следующая аксиома.

Авторы предлагают следующий алгоритм решения (любой решаемой) задачи:

Первым шагом в построении алгоритма является, согласно принципа нисходящего проектирования алгоритма, ТРИЕДИНАЯ ЗАДАЧА АЛГОРИТМИКИ – это алгоритм решения формализоанной задачи. Он представляет исходную формализованную задачу как совокупность трех подзадач (вспомогательных алгоритмов):

При этом задачи ВводаИнформации и ВыводаРезультатом можно и нужно решать самостоятельно.

В заключении отметим, что данный материал нужно использовать в 10–11-х классах. Для его проработки с учениками требуется не менее 1часа.

Источник

Тест с ответами на тему: “Программирование”

I вариант.

1. Когда необходимо составлять блок-схему программы:
а) До начала составления самой программы +
б) В процессе составления программы
в) После составления программы

2. Наиболее наглядной формой описания алгоритма является структурно-стилизованный метод:
а) словесное описание алгоритма
б) представление алгоритма в виде схемы +
в) язык программирования высокого уровня

4. В графических схемах алгоритмов стрелки направлений на линиях потоков:
а) необходимо рисовать, если направление потока снизу вверх и справа налево +
б) можно рисовать или не рисовать
в) рисовать не нужно

5. Разработкой алгоритма решения задачи называется:
а) точное описание данных, условий задачи и ее целого решения
б) сведение задачи к математической модели, для которой известен метод решения
в) определение последовательности действий, ведущих к получению результатов +

6. Языком высокого уровня является:
а) Ассемблер
б) Фортран +
в) Макроассемблер

7. Как называется алгоритм, в котором действия выполняются друг за другом, не повторяясь:
а) циклическим
б) разветвленным
в) линейным +

8. Разработке алгоритма предшествует:
а) постановка задачи, разработка математической модели +
б) постановка задачи, разработка математической модели, выбор метода решения
в) постановка задачи, выбор метода решения, проектирование программ

9. Символьный тип данных объявляется служебным словом:
а) STRING
б) WORD
в) CHAR +

10. В операторе присваивания summa := sqr(x)+3*a переменными являются:
а) sqr,x,a
б) a, x, summa +
в) summa, sqr, x, a

11. Процедура INC(x,k):
а) увеличивает значение переменной х на величину k +
б) преобразует десятичное число х в строку из k символов
в) уменьшает значение переменной х на величину k

12. Записью действительного числа с плавающей точкой является:
а) 48.0001
б) 1.0E01 +
в) –1.0533333

13. Вещественный тип данных объявляется служебным словом:
а) REAL +
б) INTEGER
в) LONGINT

14. Оператор цикла с постусловием:
а) For … to…do
б) While…do
в) Repeat… until +

15. Логический тип данных объявляется служебным словом:
а) BOOLEAN +
б) BYTE
в) LOGIC

16. Раздел переменных определяется служебным словом:
а) LABEL
б) VAR +
в) TYPE

17. В языке Паскаль пустой оператор помечаться:
а) может, но в исключительных ситуациях
б) не может
в) может +

18. Раздел типов определяется служебным словом:
а) BEGIN
б) TYPE +
в) LABEL

19. Какие из приведенных типов данных относятся к целочисленному типу данных:
а) comp, double
б) integer, real
в) integer, word, longint +

20. Из приведенных операторов описания переменных неправильно объявлены переменные:
а) var a,b:real;c:real
б) VAR f,g,d,t:INTEGER;I,t:REAL +
в) var I,j,max,min: real

II вариант.

1. Какие из приведенных типов данных относятся к вещественному типу данных:
а) real, single, extended +
б) word, double
в) byte, real

2. Для вычисления экспоненты применяется процедура:
а) SQR(X)
б) EXP(X) +
в) TRUNC(X)

3. Результатом выполнения фрагмента программы S:=-5;x:=0;repeat s:=s*(x+2);x:=x+1; until x =L) or (A =L) and (A>=M) and (L
в) (A>=L) and (A

Источник

Основные принципы разработки алгоритмов.

Список литературы: 1. Основы программирования в среде Турбо Паскаль 7.0: Методические указания/ Рязан. гос. радиотехн. акад.; Сост. В.В. Белов, В.И. Чистякова. Рязань, 2005. 2. Новичков В.С., Панфилова Н.И., Пылькин А.Н. Алгоритмизация и программирование на Турбо Паскале: Учебное пособие. – М.: Горячая линия – Телеком, 2005. 3. Москвитина О.А., Новичков В.С., Пылькин А.Н. Сборник примеров и задач по программированию: Учебное пособие. – М.: Горячая линия – Телеком, 2007.

Основы алгоритмизации.

План.

1. Этапы решения задачи на ЭВМ.

2. Алгоритм и его свойства.

3. Способы записи алгоритмов.

4. Основные принципы разработки алгоритмов.

Этапы решения задачи на ЭВМ.

Работа по решению любой задачи с использованием компьютера делится на следующие взаимосвязанные этапы (приведенное разделение является условным):

1. Постановка задачи.

2. Формализация задачи.

3. Построение алгоритма.

4. Составление программы на языке программирования.

5. Отладка и тестирование программы.

6. Проведение расчетов и анализ полученных результатов.

Часто эту последовательность называют технологической цепочкой решения задачи на ЭВМ. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5.

На этапе постановки задачи должно быть четко сформулировано, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимых для получения решения, здесь выясняется, существует ли решение поставленной задачи и единственно ли оно.

После постановки условия осуществляется «перевод» задачи на язык математики, то есть составляется система математических формул, уравнений, отношений, описывающих поведение исследуемого объекта, так получаем модель, которую обычно называют математической мо­делью. Таким образом, формализация равносильна получению соответствующей математической модели.

Третий этап — построение алгоритма. Данный этап заключается в разложении вы­числительного процесса на возможные составные части, установлении порядка их следования, описании содержания каждой такой части в той или иной форме и последующей проверке, которая должна показать, обеспечивается ли реализация выбранного метода. В большинстве случаев не удается сразу получить удовлетворительный результат, поэтому со­ставление алгоритма проводится методом проб и устранения ошибок и для получения окончательного варианта требуется несколько шагов коррекции и анализа.

Опытные программисты часто сразу пишут программы на языках, не прибегая к каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам). Однако в учебных целях полезно использовать эти средства, а затем переводить полученный алгоритм на язык программирования.

Первые три этапа предусматривают работу без компьютера. Дальше следует собственно программирование на определенном языке, в определенной системе программирования.

Разра­ботанный на третьем этапе алгоритм решения задачи необходимо изложить на специальном, понятном ЭВМ языке, который называется языком программирования. Алгоритм, записанный на языке программирования, называется программой.

На пятом этапе выясняется правильность написания программы, выявляются смысловые и синтаксические ошибки и т. п. За­тем программа вводится в память ЭВМ и ошибки, оставшиеся незамеченными, выявляются уже непосредственно с помощью машины. На этом же этапе производят тестирование программы, то есть проверку при известных частных условиях.

Только после того как появится полная уверенность, что программа обеспечивает получение правильных результатов, можно приступать непосредственно к расчетам по программе. Последний шестой этап — это использование уже разработанной программы в практических целях.

Таким образом, программист должен обладать следующими знаниями и навыками:

• уметь строить алгоритмы;

• знать языки программирования;

• уметь работать в соответствующей системе программирования.

Алгоритм и его свойства.

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi — латинского написания имени Мухаммеда аль-Хорезми (787—850), выдающегося арабского математика. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел — вот первые алгоритмы в математике. Правила алгебраических преобразований, способы вычислений корней уравнений также можно отнести к математическим алгоритмам.

В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем.

Далее, изучая понятие алгоритма, мы будем предполагать, что его исполнителем является автоматическое устройство, а именно компьютер. Это накладывает на запись алгоритма целый ряд обязательных требований. Сформулируем эти требования в виде перечня свойств, которыми должны обладать алгоритмы, адресуемые к исполнению на ЭВМ:

— Дискретность. Процесс решения задачи должен быть разбит на упорядоченную последовательность отдельных предписаний (правил, директив, команд), образующих прерывную (или, как говорят, дискретную) структуру алгоритма: только выполнив требования одного предписания можно присту­пить к исполнению следующего;

— Понятность. Исполнитель может выполнить алгоритм, если он ему понятен, т.е. записан на понятном ему языке и содержит предписания, которые исполнитель может выполнить. Набор действий, которые могут быть выполнены исполнителем, называются системой команд исполнителя. Алгоритм не должен содержать описания действий, не входящих в систему команд исполнителя.

— Конечность (результативность) – выполнение алгоритма решения задачи должно закончиться за конечное число шагов и должен быть получен конечный результат по поводу решения поставленной задачи.

— Эффективность. Эффективность алгоритма часто определяет возможность его практической реализации и может рассматриваться с разных позиций: с точки зрения времени выполнения, сложности, затраченных ресурсов, информационно-программного обеспечения.

Свойства массовости и эффективности не являются необходимыми свойствами алгоритма. Они скорее определяет качество алгоритма; в то же время свойства дискретности, понятности, детерминированности, результативности являются необходимыми (иначе это не алгоритм).

Перечисленные свойства алгоритма, по существу, являются нефор­мальным его определением. Объединяя их в одно целое, мы можем сфор­мулировать это определение следующим образом:

Алгоритм — это полное и точное описание конечной последовательности действий, которые исполнитель должен выпол­нить, чтобы за конечное время перейти от исходных дан­ных к искомому результату.

Как известно, всякий алгоритм (программа) составляется для конкретного исполнителя в рамках его системы команд. Исполняя алгоритм, исполнитель не вникает в смысл того, что он делает, но вместе с этим он может получить нужный результат. В таких случаях говорят, что исполнитель действует формально. При программировании для ЭВМ исполнителем является компьютер. Точнее говоря, исполнителем является комплекс ЭВМ + Система программирования (СП). Программист составляет программу на том языке, на который ориентирована СП.

Способы записи алгоритмов.

В процессе разработки алгоритма могут использоваться различные способы его описания, отличающиеся по простоте, наглядности, ком­пактности, степени формализации, ориентации на машинную реализацию и другим показателям. В практике программирования наибольшее распространение получили:

— словесное описание (кулинарные рецепты);

— псевдокод, когда используется формальный алгоритмический язык;

— задание алгоритма в виде цепочки формул;

— графическое описание алгоритма в виде структурограммы или блок-схемы.

Изображение алгоритмов в виде структурограмм (схем Насси-Шнейдермана) пред­ставляет собой попытку использования требований структурного про­граммирования в схемах алгоритмов. Данный способ позволяет изображать схему пе­редач управления с помощью представления вложенности структур. Структурограммалучше отражает структуру алгоритма, чем блок-схема. Но для ее составления требуется много места.

Блок-схема – это наглядное графическое изображение алгоритма с элементами словесной записи, при котором отдельные действия (этапы) алгоритма изображаются при помощи различных геометрических фигур (блоков), а связи между этими этапами указываются при помощи стрелок, соединяющими эти фигуры. Различным (по типу выполняемых действий) блокам соответствуют различные геометрические фигуры. Приняты определенные стан­дарты графических изображений блоков:

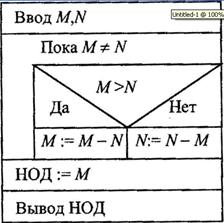
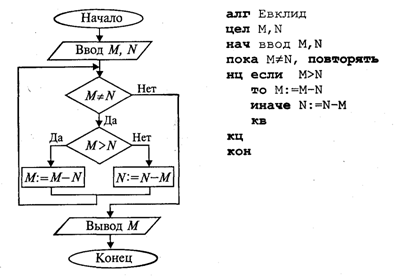
Рассмотрим алгоритм решения задачи определения наибольшего общего делителя (НОД) двух целых положительных чисел M, N, представленный различными способами.

Известен алгоритм решения этой задачи, получивший название алгоритм Евклида:

п 1. Если числа равны между собой, то взять в качестве НОД любое
из них.

п 2. Если числа не равны между собой, то большее из чисел заменить
их разностью и вернуться к п.1

Более детально алгоритм Евклида может быть представлен следую­щей словесной записью:

если М > N, то М := M-N; иначе N := N—M.

Структурограмма, блок-схема и запись на алгоритмическом языке данного алгоритма имеют соответственно вид:

Для описания алгоритмов в дальнейшем мы будем использовать блок-схемы, поскольку они являются наглядным и простым способом представления алгоритмов. Их обычно используют на первом этапе алгоритмизации, при разработке общей структуры алгоритма, так как блок-схемы позво­ляют отчетливо представить себе алгоритм в целом и проследить все ло­гические связи между отдельными частями алгоритма, проверить все возможные варианты решения поставленной задачи и выявить допущен­ные ошибки или неточности. Для проверки правильности алгоритма может быть построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм.

Основные принципы разработки алгоритмов.

Прошло уже более полувека со времени появления первой ЭВМ. Все это время вычислительная техника бурно развивалась. Менялась элементная база ЭВМ, росли быстродействие, объем памяти, менялись средства взаимодействия человека с машиной. Безусловно, эти изменения сказывались самым непосредственным образом на работе программиста. Определенный общепринятый способ производства чего-либо (в данном случае — программ) называют технологией. Далее мы будем говорить о технологии программирования.

С ростом памяти и быстродействия ЭВМ, с совершенствованием языков программирования и трансляторов с этих языков проблема экономичности программы становится менее острой. Все более важной качественной характеристикой программ становится их простота, наглядность, надежность. С появлением машин третьего поколения эти качества стали основными.

В конце 60-х — начале 70-х гг. XX столетия вырабатывается дисциплина, которая получила название структурного программирования, в рамках которой сформировался так называемый структурный подход к конструированию и оформлению алгоритмов. Ее появление и развитие связано с именами Э. В. Дейкстры, Х.Д.Милса, Д. Е. Кнута и других ученых. Структурное программирование до настоящего времени остается основой технологии программирования. Соблюдение его принципов позволяет программисту быстро научиться писать ясные, безошибочные, надежные программы.

Структурный подход – это совокупность приемов и правил разработки алгоритмов, имеющих четкую и ясную структуру. Выделение четкой и ясной структуры алгоритма уменьшает количество ошибок на этапе разработки алгоритма, упрощает их контроль и модификацию. Алгоритм становится более удобным.

По своей сути структурный подход есть отказ от беспорядочного стиля в алгоритмизации (в частности, отказ от оператора GOTO) и опре­деление ограниченного числа стандартных приемов построения легко чи­таемых алгоритмов с ясно выраженной структурой. Теоретически фун­даментом этого подхода является теорема о структурировании (которая была строго доказана в теории программирования), из кото­рой следует, что алгоритм для решения любой логической задачи можно составить только из структур «следование, ветвление, цикл с предусловием». Их называют базовыми алгоритмическими структурами.

Однако с целью создания более компактных и наглядных алгорит­мов дополнительно используются следующие управляющие структуры: а) сокращенная запись ветвления; б) структура выбора; в) структура цик­ла с параметром; г) структура цикла с постусловием.

Следование — структура, реализующая вычислительный процесс, в котором отдельные этапы вычислений должны выполняться последовательно друг за другом. Это линейная последовательность действий, в которой каждый блок может содержать в себе как простую команду, так и сложную структуру, но обязательно должен иметь один вход и один выход.

Ветвление — структура, реализующая вычислительный процесс, в котором в зависимости от истинности или ложности условия должно выполняться либо одно, либо другое действие (управление передается одному из двух блоков), после чего происходит выход на общее продолжение.

Вначале проверяется условие (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется действие 1 — последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется действие 2 (отрицательная ветвь).

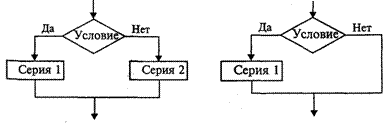Действие 1 или действие 2 может в свою очередь содержать несколько этапов.

Сокращенная запись ветвления имеет место, когда на ветви «нет» пусто.

Вычислительные процессы с многократным повторением однотип­ных вычислений/действий для различных значений входящих вели­чин/данных называются циклическими, повторяемые участки вычисле­ний – циклами.

Для организации циклов в алгоритмах необходимо предусмотреть:

• модификацию/изменение значений переменных цикла перед каждым новым его повторением;

Существует несколько видов циклов:

c. цикл с параметром – когда известно число повторений тела цикла.

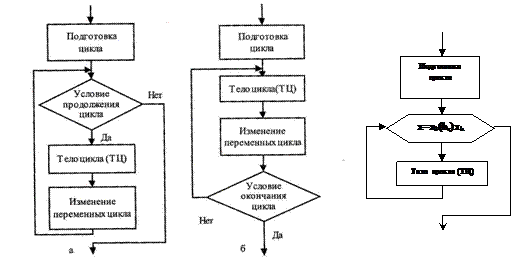
Теоретически необходимым и достаточным является лишь первый тип цикла — цикл с предусловием. Любой циклический алгоритм можно построить с его помощью.

Цикл с предусловием применяется при необходимости выполнить какие-либо действия несколько раз, пока условие истинно. Особенность этого цикла в том, что он может не выполнится ни разу, так как первая проверка условия выхода из цикла происходит до того, как будет выполнено тело цикла. Тело цикла повторяет свое выполнение, если условие истинно. Повторение кончается, когда условие станет ложным.

Цикл с постусловием применяется при необходимости выполнить какие-либо действия несколько раз до выполнения некоторого условия. Особенность этого цикла в том, что он всегда выполняется хотя бы один раз, так как первая проверка условия выхода из цикла происходит после того, как тело цикла выполнено. Тело цикла повторяет свое выполнение, если условие ложно. Повторение кончается, когда условие станет истинным.

В циклах с параметром (с известным числом повторений) всегда можно определить переменную, связанную с числом повторений цикла, значение которой изменяется по заданному закону: от начального до конечного с постоян­ным шагом. Такая переменная используется для управления циклом: в условии окончания цикла осуществляется сравнение текущего значения переменной с заданным порогом. Эту переменную именуют параметром цикла.

Множественный выбор явля­ется обобщением разветвления, когда в зависимости от значения выражения (i) вы­полняется одно из нескольких действий. При i=1 выполня­ется действие s1, при i=2— действие s2 и т. д., ), после чего происходит выход на общее продолжение.

Особенностью всех приве­денных структур является то, что они имеют один вход и один выход, и их можно соединять друг с другом в любой последовательности. В частности, каждая структура может содержать любую другую структуру в качестве одного из блоков. На основании этого можно сформулировать два основных приема использования базовых алгоритмических структур

a) присоединение – одна структура следует за другой (на блок-схеме – выход соединен со входом);

b) вложение – одна структура находится внутри другой (прямоугольник заменяется другой фигурой).

Структурный подход требует соблюдения стандарта в изображении блок-схем алгоритмов. Нестандартно изображенная блок-схема плохо читается, теряется наглядность алгоритма. Вот несколько примеров структурных блок-схем алгоритмов.

Такие блок-схемы легко читаются. Их структура хорошо воспринимается зрительно. Структуре каждого алгоритма можно дать название. У приведенных на рисунке блок-схем следующие названия:

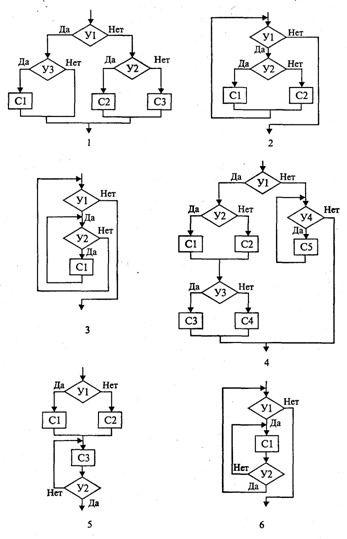
1. Вложенные ветвления.

2. Цикл с вложенным ветвлением.

3. Вложенные циклы-пока.

4. Ветвление с вложенной последовательностью ветвлений на положительной ветви и с вложенным циклом-пока на отрицательной ветви.

5. Следование ветвления и цикла-до.

6. Вложенные циклы. Внешний — цикл-пока, внутренний — цикл-до.

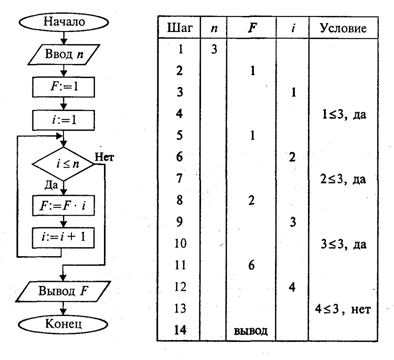
Рассмотрим следующую задачу: дано целое положительное число п. Требуется вычислить n! (n-факториал). Вспомним определение факториала:

На рисунке приведена блок-схема алгоритма. В нем используются три переменные целого типа: п — аргумент; i — промежуточная переменная; F — результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая п = 3.

Трассировка доказывает правильность алгоритма.

Дополнительно: [2] стр. 5-53

Дата добавления: 2018-06-01 ; просмотров: 3276 ; Мы поможем в написании вашей работы!

Источник