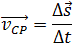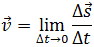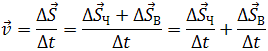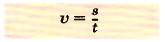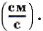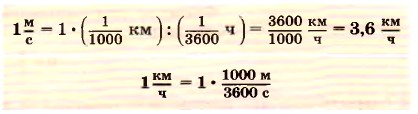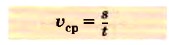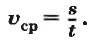Что принимают за единицу скорости

Единицы измерения скорости.

Чтобы найти координаты движущегося тела в любой момент времени, нужно знать проекции вектора перемещения на оси координат.

Самым простым видом движения является прямолинейное равномерное движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скоростью равномерного прямолинейного движения называют величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка (Δt). Так как – величина векторная, а Δt – скалярная, то скорость тоже величина векторная:

,

Скорость ( от англ. velosity) – векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчета.

По формулам, написанным в векторной форме, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях пользуются формулами, в которые входят не векторы, а их проекции на оси координат, чтобы можно было производить алгебраические действия.

Когда имеют дело с неравномерным движением, пользуются так называемой средней скоростью. Если тело совершило некоторое перемещение за промежуток времени t, то разделив на t, мы получим среднюю скорость:

Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени.

При движении тела по окружности пользуются вектором перемещения, как и при прямолинейном движении. Но часто более удобным оказывается характеризовать изменение положения тела (материальной точки) при движении по окружности другой величиной – углом поворота (j). При равномерном движении точки по окружности углы поворота радиуса за любые равные промежутки времени будут одинаковы. Разделив угол поворота на время, за которое совершен поворот, мы получим так называемую угловую скорость вращения этого радиуса (w):

В отличие от угловой скорости w скорость υ, определяемую отношением длины пройденного пути l (скалярная величина) к соответствующему промежутку времени t, называют линейной скоростью:

Для скорости не надо выбирать специальную единицу.

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за 1 с совершает перемещение в 1м (1 м/с – производная единица системы СИ).

В мореходной практике распространена специальная единица скорости, носящая название узел. Узел — это скорость такого движения, при котором тело проходит за один час одну морскую милю. 1 узел = 0,514 м/с.

Итак, под термином «скорость» понимают быстроту изменения какой-либо величины в зависимости от другой (в основном – изменения во времени, а также в пространстве и др.).

Кроме вышеперечисленных существуют также угловая скорость (рад/с), скорость изменения температуры, скорость химической реакции и т. д.

Источник

Единицы измерения скорости.

Чтобы найти координаты движущегося тела в любой момент времени, нужно знать проекции вектора перемещения на оси координат.

Самым простым видом движения является прямолинейное равномерное движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скоростью равномерного прямолинейного движения называют величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка (Δt). Так как – величина векторная, а Δt – скалярная, то скорость тоже величина векторная:

,

Скорость ( от англ. velosity) – векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчета.

По формулам, написанным в векторной форме, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях пользуются формулами, в которые входят не векторы, а их проекции на оси координат, чтобы можно было производить алгебраические действия.

Когда имеют дело с неравномерным движением, пользуются так называемой средней скоростью. Если тело совершило некоторое перемещение за промежуток времени t, то разделив на t, мы получим среднюю скорость:

Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени.

При движении тела по окружности пользуются вектором перемещения, как и при прямолинейном движении. Но часто более удобным оказывается характеризовать изменение положения тела (материальной точки) при движении по окружности другой величиной – углом поворота (j). При равномерном движении точки по окружности углы поворота радиуса за любые равные промежутки времени будут одинаковы. Разделив угол поворота на время, за которое совершен поворот, мы получим так называемую угловую скорость вращения этого радиуса (w):

В отличие от угловой скорости w скорость υ, определяемую отношением длины пройденного пути l (скалярная величина) к соответствующему промежутку времени t, называют линейной скоростью:

Для скорости не надо выбирать специальную единицу.

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за 1 с совершает перемещение в 1м (1 м/с – производная единица системы СИ).

В мореходной практике распространена специальная единица скорости, носящая название узел. Узел — это скорость такого движения, при котором тело проходит за один час одну морскую милю. 1 узел = 0,514 м/с.

Итак, под термином «скорость» понимают быстроту изменения какой-либо величины в зависимости от другой (в основном – изменения во времени, а также в пространстве и др.).

Кроме вышеперечисленных существуют также угловая скорость (рад/с), скорость изменения температуры, скорость химической реакции и т. д.

Источник

Скорость

Скорость – это количественная характеристика движения тела.

Средняя скорость – это физическая величина, равная отношению вектора перемещения 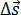точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения . Средняя скорость определяется по формуле:

Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

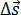
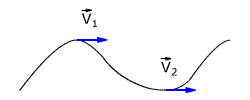
Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения к очень малому промежутку времени, за который это перемещение произошло.

Вектор мгновенной скорости направлен по касательной к траектории движения тела (рис. 1.6).

Рис. 1.6. Вектор мгновенной скорости.

В системе СИ скорость измеряется в метрах в секунду, то есть единицей скорости принято считать скорость такого равномерного прямолинейного движения, при котором за одну секунду тело проходит путь в один метр. Единица измерения скорости обозначается м/с. Часто скорость измеряют в других единицах. Например, при измерении скорости автомобиля, поезда и т.п. обычно используется единица измерения километр в час: или

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический закон сложения скоростей.

Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и самой подвижной системы отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч. По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скоростей поезда и человека, то есть и

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том, что скорость – это векторная величина.

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта. Поезд, который движется по этой дороге – это подвижная система отсчёта. Вагон, по которому идёт человек, является частью поезда.

Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5 км/ч. Обозначим её буквой _Ч.

Скорость поезда (а значит и вагона) относительно неподвижной системы отсчёта (то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой _В. Иначе говоря, скорость поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.

Скорость человека относительно железной дороги (относительно неподвижной системы отсчёта) нам пока неизвестна. Обозначим её буквой .

Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY, а с подвижной системой отсчёта – систему координат X_ПО_ПY_П (см. также раздел Система отсчёта). А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта, то есть относительно железной дороги.

= _Ч + _B

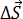
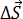
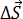
Это закон сложения перемещений. В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.

Рис. 1.7. Закон сложения перемещений.

Закон сложения перемещений можно записать так:

= Δ_Ч • Δt + Δ_B • Δt

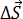
Скорость человека относительно железной дороги равна: Так как

= _Ч + _B

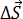
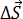
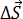
Скорость человека относительно вагона: Скорость вагона относительно железной дороги: Поэтому скорость человека относительно железной дороги будет равна: Это закон сложения скоростей:

Источник

§ 16. Скорость. Единицы скорости

Мы часто говорим, что одни тела движутся быстрее, другие медленнее. Например, по шоссе шагает турист, мчится автомобиль, в воздухе летит самолёт. Допустим, что все они движутся равномерно, тем не менее движение этих тел будет отличаться.

Автомобиль движется быстрее пешехода, а самолёт быстрее автомобиля. В физике величиной, характеризующей быстроту движения тел, является скорость.

Предположим, что турист за 1 ч проходит 5 км, автомобиль 90 км, а самолёт пролетает 850 км. Тогда говорят, что скорость туриста 5 км в час, скорость автомобиля 90 км в час, а скорость самолёта 850 км в час.

Скорость при равномерном движении тела показывает, какой путь оно прошло в единицу времени.

Таким образом, используя понятие скорости, мы можем теперь сказать, что турист, автомобиль и самолёт движутся с различными скоростями.

При равномерном движении скорость тела остаётся постоянной.

Если велосипедист проезжает в течение 5 с путь, равный 25 м, то его скорость будет равна 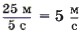(5 метров в секунду).

Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени, разделить на этот промежуток времени.

Скорость обозначают буквой υ, путь — s, время — t.

Формула для нахождения скорости будет иметь вид:

В Международной системе (СИ) скорость измеряют в метрах в секунду

Это значит, что за единицу скорости принимается скорость такого равномерного движения, при котором за 1 секунду тело проходит путь, равный 1 метру.

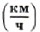
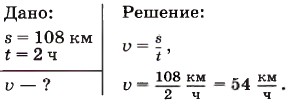
Скорость тела можно измерять также в километрах в час ; километрах в секунду ; сантиметрах в секунду

П р и м е р. Поезд, двигаясь равномерно, за 2 ч проходит путь, равный 108 км. Вычислите скорость движения поезда.

Запишем условие задачи и решим её.

Выразим скорость поезда в единицах СИ, т. е. километры переведём в метры, а часы в секунды:

Таким образом, числовое значение скорости зависит от выбранной единицы.

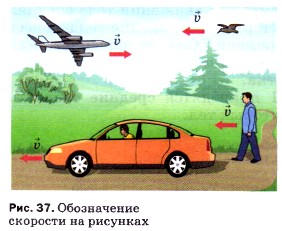
Скорость, кроме числового значения, имеет и направление.

Если требуется узнать, где будет находиться через 2 ч самолёт, вылетевший из Владивостока, то необходимо знать не только значение его скорости, но и её направление.

Величины, которые, кроме числового значения (модуля), имеют ещё и направление, называют векторными.

Скорость — это векторная физическая величина.

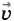
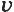
Все векторные величины обозначают соответствующими буквами со стрелочкой. Например, скорость обозначается буквой со стрелочкой, а её значение — модуль скорости той же буквой, но без стрелочки .

На рисунках стрелкой показывают направление скорости, т. е. направление движения тела (рис. 37).

Некоторые физические величины не имеют направления. Они характеризуются только числовым значением. Это путь, время, объём, длина и др. Они являются скалярными величинами.

Если при движении тела его скорость изменяется от одного участка пути к другому, то такое движение является неравномерным.

Для характеристики неравномерного движения тела вводят понятие средней скорости.

Например, поезд от Москвы до Санкт-Петербурга идёт со скоростью 80 км/ч. Какую скорость имеют в виду? Ведь скорость поезда на остановках равна нулю, после остановки — увеличивается, а перед следующей остановкой — уменьшается.

В данном случае поезд движется неравномерно, а значит, скорость, равная 80 км/ч, — это средняя скорость движения поезда. Она определяется почти так же, как и скорость при равномерном движении.

Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на всё время движения:

Следует напомнить, что только при равномерном движении отношение 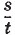за любой промежуток времени будет постоянно.

При неравномерном движении тела средняя скорость характеризует движение тела за весь промежуток времени. Она не поясняет, как двигалось тело в различные моменты времени этого промежутка.

В таблице 1 приводятся средние скорости движения некоторых тел.

Вопросы

1. Что показывает скорость тела при равномерном движении?
2. По какой формуле определяют скорость тела, если известен его путь и время, за которое он пройден?
3. Какова единица измерения скорости в СИ?
4. Чем, кроме числового значения, характеризуется скорость тела?
5 Как определяют среднюю скорость при неравномерном движении?

Упражнение 3

1. Выразите скорости тел: 90км/ч и 36 км/ч в м/с.
2. Поезд идёт со скоростью 72 км/ч. Выразите его скорость в м/с.
3. Гоночный автомобиль за 10 мин проезжает путь, равный 50 км. Определите его среднюю скорость.
4. Лучшие конькобежцы дистанцию 1500 м пробегают за 1 мин 52,5 с. С какой средней скоростью они проходят эту дистанцию?
5. Лыжник, спускаясь с горы, проходит 50 м за 5 с. Спустившись с горы и продолжая двигаться, он до полной остановки проходит ещё 30 м за 15 с. Найдите среднюю скорость лыжника за всё время движения.

Задание

Найдите с помощью Интернета фамилии советских лётчиков, совершивших впервые в мире беспосадочный перелёт Москва—Северный полюс—США. Известно, что расстояние 8582 км они пролетели за 63 ч 16 мин. Определите, с какой скоростью летел самолёт.

Источник

§ 12. Равномерное движение. Скорость равномерного движения

Назовите возможные единицы скорости движения тела.

Приведите примеры физических величин, связанных прямой пропорциональной зависимостью.

1. Среди разнообразных механических движений встречается равномерное движение.

Равномерным называют такое движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.

Например, если поезд на достаточно большом перегоне проходит за каждый час 60 км, за каждые полчаса 30 км, за каждую минуту 1 км ит.д., то его движение равномерное. Равномерное движение можно наблюдать на опыте с движущейся тележкой, на которой установлена капельница (рис. 29). Через равные промежутки времени из капельницы падают капли. Измерив расстояния между следами от капель, можно увидеть, что они одинаковы, значит, тележка движется равномерно.

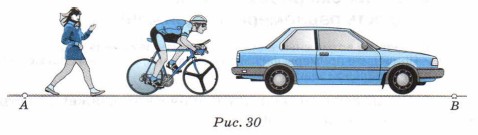
2. Представьте себе, что из пункта А в пункт В равномерно движутся автомобиль, велосипедист и пешеход (рис. 30). Хотя все три движения равномерные, они отличаются друг от друга: автомобиль движется быстрее всех и первым доедет до пункта В; затем туда приедет велосипедист и, наконец, дойдёт пешеход. Следовательно, равномерные движения этих трёх тел различаются быстротой движения, иначе говоря, скоростью.

3. Чтобы определить скорость равномерно движущегося тела, нужно разделить путь, пройденный телом, на время, в течение которого этот путь пройден:

Скорость тела при равномерном движении показывает, какой путь проходит тело в единицу времени.

Скорость — это физическая величина. Её обозначают буквой v, путь — s, время — t. Следовательно, можно записать формулу для нахождения скорости:

4. За единицу скорости принимают скорость такого равномерного движения, при котором тело за единицу времени (1 с) проходит путь, равный единице длины (1 м).

Основной единицей скорости является метр в секунду Кроме неё, возможны и другие: миллиметр в секунду сантиметр в секунду километр в час Так, скорость движущегося транспорта принято выражать в Например, скорость автомобиля — скорость велосипедиста — А скорость улитки удобнее измерять в более мелких единицах, так скорость виноградной улитки около

Источник