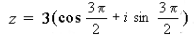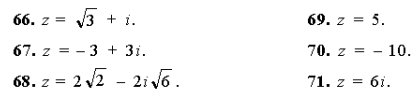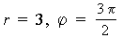Что принято за мнимую единицу
Мнимая единица – число на грани мистики
Человеку не сведущим в математике и физике рассуждения о мнимой единице представляется полным бредом. Например, квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Отсюда ясно, что квадратные корни из отрицательных чисел не могут находиться среди возможных действительных чисел. Следовательно, нам не остается ничего другого, как признать их невозможными числами.
Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел. Это было сделано китайскими математиками во II веке до н. э. Отрицательные числа не так просты. Представьте, сколько будет 3 – 4? Как можно отнять 4 барана от 3? Отрицательные числа рассматривались как полная чушь. Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число Е и много еще чего, не понимал отрицательные числа так же хорошо, как
мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений. Древнегреческие математики считали «настоящими» только натуральные числа.
То, что называют мнимым числом, на самом деле частный случай комплексного числа. Это число настоящим числом назвать нельзя. Учебники описывают его как величину, которая, будучи возведенной в квадрат, дает минус один. Другими словами, это сторона квадрата с отрицательной площадью. В реальности такого не бывает. Впервые понятие «мнимая величина» использовал Кардано (1545). Он решал задачу с помощью квадратных уравнений
Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс означает связь, сочетание, совокупность понятий, предметов, явлений образующих единое целое. В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изобразить комплексное число z = a + b × i точкой m (a, b) на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M, а вектором, идущим в эту точку из начала координат. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. В дальнейшем Леонард Эйлер (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) получил знаменитую формулу, и открыл комплексным числам дорогу в самые различные области математики и ее приложений.
Комплексные числа – расширили понятие числа. В 1843 году ирландский математик Уильям Гамильтон предложил четырехмерную систему комплексных чисел, которая стала первой гиперкомплексной системой, названную кватернионами. Теория кватернионов вскоре стала одним из источников дальнейшего развития математики и ее приложений.
Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения.
Комплексные числа
1. Понятие мнимой единицы
Допустим, что существует такое число, квадрат которого равен – 1. Обозначим это число буквой i; тогда можно записать: i 2 = – 1.
Число i будем называть мнимой единицей (i – начальная буква французского слова imaginaire – «мнимый»), а предыдущее равенство будем считать определением мнимой единицы.
Из этого равенства находим
Введение мнимой единицы позволяет нам теперь извлекать корни квадратные из отрицательных чисел.
2. Степени мнимой единицы
Рассмотрим степени мнимой единицы:
Если выписать все значения степеней числа i, то мы получим такую последовательность: i, – 1, – i, 1, i, – 1, – i, 1 и т. д. Легко видеть, что значения степеней числа i повторяются с периодом, равным 4.
Таким образом, если показатель степени числа i делится на 4, то значение степени равно 1; если при делении показателя степени на 4 в остатке получается 1, то значение степени равно i; если при делении показателя степени на 4 получается остаток 2, то значение степени равно – 1; наконец, если при делении на 4 остаток равен 3, то значение степени равно – i. Пользуясь этим, можно вычислять любую степень числа i.
Соответственно получим i 28 = 1; i 33 = i; i 135 = – i.
3. Определение комплексного числа
Мы знакомы с действительными числами и с мнимыми единицами. Рассмотрим теперь числа нового вида.
Определение 1. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, будем называть комплексными.
Число a будем назвать действительной частью комплексного числа, bi – мнимой частью комплексного числа, b – коэффициентом при мнимой части. Возможны случаи, когда действительные числа a и b могут быть равными нулю. Если a = 0, то комплексное число bi называется чисто мнимым. Если b = 0, то комплексное число a + bi равно a и называется действительным. Если a = 0 и b = 0 одновременно, то комплексное число 0 + 0i равно нулю. Итак, мы получили, что действительные числа и чисто мнимые числа представляют собой частные случаи комплексного числа.
Запись комплексного числа в виде a + bi называется алгебраической формой комплексного числа.
Два комплексных числа a + bi и c + di условились считать равными тогда и только тогда, когда в отдельности равны их действительные части и коэффициенты при мнимой единице, т. е. a + bi = c + di, если a = c и b = d.
Пример 2. Найти x и y из равенства:
Решение. а) Согласно условию равенства комплексных чисел имеем 3y = 15, 5x = – 7. Отсюда
б) Из условия равенства комплексных чисел следует
Умножив второе уравнение на 3 и сложив результат с первым уравнением, имеем 5x = 25, т. е. x = 5. Подставим это значение во второе уравнение: 5 – y = 6, откуда y = – 1. Итак, получаем ответ: x = 5, y = – 1.
8–13. Найдите значения x и y из равенств:
4. Действия над комплексными числами в алгебраической форме
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
14–21. Произведите сложение и вычитание комплексных чисел:
14. (3 + 5i) + (7 – 2i).
15. (6 + 2i) + (5 + 3i).
16. (– 2 + 3i) + (7 – 2i).
17. (5 – 4i) + (6 + 2i).
18. (3 – 2i) + (5 + i).
19. (4 + 2i) + (– 3 + 2i).
20. (– 5 + 2i) + (5 + 2i).
21. (– 3 – 5i) + (7 – 2i).
22–29. Произведите умножение комплексных чисел:
Замечание. При выполнении умножения можно использовать формулы:
Пример 4. Выполнить действия:
а) (2 + 3i) 2 = 4 + 2 Ч 2 Ч 3i + 9i 2 = 4 + 12i – 9 = – 5 + 12i;
б) (3 – 5i) 2 = 9 – 2 Ч 3 Ч 5i + 25i 2 = 9 – 30i – 25 = – 16 – 30i;
в) (5 + 3i) 3 = 125 + 3 Ч 25 Ч 3i + 3 Ч 5 Ч 9i 2 + 27i 3 ;
так как i 2 = – 1, а i 3 = – i, то получим (5 + 3i) 3 = 125 + 225i – 135 – – 27i = – 10 + 198i.
30–37. Выполните действия:
Рассмотрим теперь применение формулы
Пример 5. Выполнить действия:
а) (5 + 3i)(5 – 3i) = 5 2 – (3i) 2 = 25 – 9i 2 = 25 + 9 = 34;
б) (2 + 5i)(2 – 5i) = 2 2 – (5i) 2 = 4 + 25 = 29;
в) (1 + i)(1 – i) = 1 2 – i 2 = 1 + 1 = 2.
38–43. Выполните действия:
Обратим внимание на то, что при использовании формулы (*) всегда получается частный случай комплексного числа – действительное число, а комплексные числа, которые мы умножаем, являются сопряженными.
Определение 2. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
Мы видим, что произведение двух сопряженных чисел всегда равно действительному числу. Воспользуемся этим свойством для выполнения деления двух комплексных чисел. Чтобы выполнить деление, произведем дополнительное действие: умножим делимое и делитель на комплексное число, сопряженное делителю.
Пример 6. Выполнить деление:
Произведем умножение для делимого и делителя в отдельности:
44–55. Выполните деление:
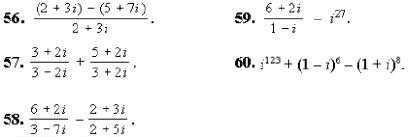
56–60. Выполните действия:
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен.
Пример 7. Решите уравнение:
Решение. а) Найдем дискриминант по формуле
Так как a = 1, b = – 6, c = 13, то
D = (– 6)2 – 4 Ч 1 Ч 13 = 36 – 52 = – 16;
Корни уравнения находим по формулам
б) Здесь a = 9, b = 12, c = 29. Следовательно,
D = b 2 – 4ac =12 2 – 4 Ч 9 Ч 29 = 144 – 1044 = – 900,
Находим корни уравнения:
Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня.
62–65. Решите уравнения:
62. x 2 – 4x + 13 = 0.
63. x 2 + 3x + 4 = 0.
64. 2,5x 2 + x + 1 = 0.
65. 4x 2 – 20x + 26 = 0.5. Геометрическая интерпретация комплексного числа
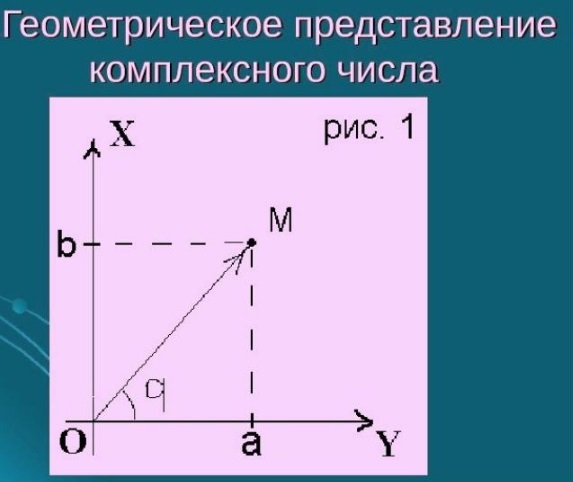
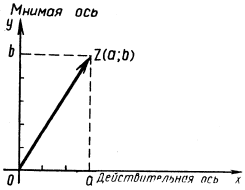
Комплексное число z = a + bi можно изобразить точкой Z плоскости с координатами (a; b) (рис. 1). Для этого выберем на плоскости декартову прямоугольную систему координат. Действительные числа изображаются точками оси абсцисс, которую называют действительной (или вещественной) осью; чисто мнимые числа – точками оси ординат, которую будем называть мнимой осью.
Каждой точке плоскости с координатами (a; b) соответствует один и только один вектор с началом O(0; 0) и концом Z(a; b). Поэтому комплексное число z = a + bi можно изобразить в виде вектора с началом в точке O(0; 0) и концом в точке Z(a; b).
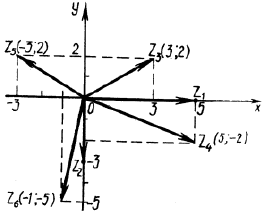
Решение. Заданные числа изображены на рис. 2.
6. Тригонометрическая форма комплексного числа
Пусть комплексное число z = a + bi изображено в виде вектора с началом в точке O(0; 0) и концом Z(a; b) (рис. 3).
Обозначив модуль комплексного числа буквой r. (1)
Из соотношений
и
Если в запись комплексного числа z вместо a и b подставить эти значения, то получим
Таким образом, мы получили новую форму записи комплексного числа:
которая называется тригонометрической формой комплексного числа.
Сформулируем правило перехода от алгебраической формы комплексного числа к тригонометрической.
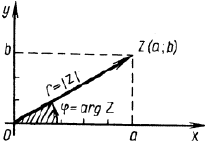
1. Находят модуль комплексного числа r, для чего используют формулу
2. Для нахождения j сначала определяют геометрически, в какой четверти находится точка z.
4. Записывают комплексное число z в тригонометрической форме.
Пример 9. Записать в тригонометрической форме комплексное число z = 1 + i.
1) Так как a = 1, b = 1, то
2) Изобразим число z геометрически (рис. 4). Мы видим, что числу z соответствует точка Z, лежащая в I четверти, и вектор z.
3) Составим соотношения
и
т. е.
Этим соотношениям соответствует в I четверти угол
4) Так как
то тригонометрическая форма заданного комплексного числа имеет вид
Пример 10. Записать число
в тригонометрической форме.
Решение. 1) Здесь
Следовательно,
2) Изобразим число z геометрически (рис. 5). Мы видим, что числу z соответствует точка Z, лежащая во II четверти, и вектор z.
4) Запишем заданное число в тригонометрической форме:
Пример 11. Записать в тригонометрической форме чисто мнимое число z = – 3i.
Решение. 1) Запишем данное число в виде z = 0 – 3i. Значит, a = 0, b = – 3, откуда
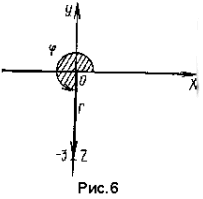
2) Точка, соответствующая геометрически числу z = – 3i, лежит на мнимой оси (рис. 6).
3) Аргумент этого числа равен
,
так как угол отсчитывается от положительного направления оси Ox против часовой стрелки.
4) Запишем данное число в тригонометрической форме:
66–71. Запишите в тригонометрической форме комплексные числа:
7. Показательная форма комплексного числа
которое называется формулой Эйлера.
Эта форма записи комплексного числа называется показательной формой.
Итак, существуют три формы записи комплексного числа:
z = a + bi – алгебраическая форма;
z = r (cos j + i sin j ) – тригонометрическая форма;
z = re ij – показательная форма.
Пример 12. Записать число
в показательной форме.
Решение. Здесь
Следовательно, показательная форма числа имеет вид
Мнимая единица
Маяковский про мнимую единицу
Мнимая единица (讠, один с точечкой) — это:
Эта вторая формулировка крайне сложна. Чтобы её понять и привести к простой, нужно разбить одно окно чем-нибудь, другое — головой. И сравнить осколки обоих стёкол и состояние головы и крыши до и после процедуры.
Содержание
История открытия [ править ]
Основные свойства [ править ]
После того, как сбрендившие учёные поняли, что такое мнимая единица, стали выводить разные формулы. Например:
2 i = 2 i e e = 21 ⋅ e e = 21 <\displaystyle 2i=<\frac <2ie>
Тождество Эйлера [ править ]
Существует следующее тождество:
Его высказал Эйлер, один из трезвых учёных, во сне. Поэтому его называют тождеством Эйлера. До сих пор учёные всего мира не понимают смысл этой формулы и удивляются её странностью. Не меньше удивления вызывает то, что этот великий математик подарил открытие миру в спящем состоянии. Он, проснувшись, показывал, что ничего не помнит, что ему «опять снились эти формулы бессмысленные». Но никто и не подумал пренебрегать великим открытием. Все без исключения должны верить тому, что сказал Эйлер, поскольку он уже сделал много великих открытий. Он просто не захотел раскрывать строгого доказательства. Известны несколько доказательств, но известны и их опровержения.
Доказательство [ править ]
e − i π ∗ e i π = ( − 1 ) ∗ ( − 1 ) <\displaystyle e^<-i\pi >*e^
В итоге мы получили верное равенство, которое вытекает из исходного, поэтому тождество Эйлера доказано!
Опровержение [ править ]
e i π + 1 = e 1 ⋅ π + 1 = e π + 1 ≠ 0 <\displaystyle e^
Опровержение опровержения [ править ]
Не верьте этому опровержению, Эйлер говорил правду. (остальные 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 472 восклицательных знака были удалены автоматическим фильтром)
Следствие 1 [ править ]
Из тождества Эйлера следует нечто совсем уж парадоксальное. Перепишем тождество Эйлера в таком виде:
Поскольку в правой части равенства стоит действительное число, значит и в левой части тоже действительное число. В таком случае мы можем смело возвести обе части этого равенства в квадрат:
Следствие 2 [ править ]
Еще раз рассмотрим вышеприведённое тождество Эйлера:
А теперь возведем обе его части в любую целую нечётную степень n:
А значит, при любом нечётном n,
Интересные факты [ править ]
Человекам далеко не сведущим в математике, физике и алгебре, да что уж там — геометрии, рассуждения о мнимой единице представляется полным бредом. Прежде чем о ней рассуждать необходимо определиться, что такое отрицательные числа в природе. Дак, вот их НЕТ. Также как не может быть отрицательной скорости. Отрицательные числа прибывают в нашем воображении из-за того, что мы принимаем какое-либо значение за НОЛЬ. К примеру рассмотрим температуру вещества, а именно абсолютный ноль по Цельсию, это −273,15 °C (-459,67° по Фаренгейту), то есть полный покой вещества, когда его атомы «обездвижены» — вот это и есть НОЛЬ. Отсюда следует отрицательные числа, которые кажутся таковыми, следует записывать в скобках, например так:(-1). Физический смысл отрицательной степени — отсутствует. i 2 = − 1 <\displaystyle i^<2>=-1> 
В итоге Эйлером доказано, что 1=-1, такой же единице только по другую сторону шкалы.
СОДЕРЖАНИЕ
Определение
Мнимое число i определяется исключительно тем свойством, что его квадрат равен −1:
.>
Точно так же, как и с любым ненулевым действительным числом:
Матрицы
Аналогичная проблема возникает, если комплексные числа интерпретируются как вещественные матрицы 2 × 2 (см. Матричное представление комплексных чисел ), потому что тогда оба
были бы решениями матричного уравнения
Все эти неоднозначности могут быть решены путем принятия более строгого определения комплексного числа и явным выбором одного из решений уравнения в качестве мнимой единицы. Например, упорядоченная пара (0, 1) в обычном построении комплексных чисел с двумерными векторами.
Правильное использование
а ⋅ б знак равно а ⋅ б <\ displaystyle <\ sqrt > \ cdot <\ sqrt > = <\ sqrt >>
а б знак равно а б <\ displaystyle <\ frac <\ sqrt > <\ sqrt >> = <\ sqrt <<\ frac <\, a \,>> \,>>>
Какие свойства мнимой единицы
Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляться также в обобщённом смысле не только для комплексных чисел[⇨].
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «−i» и «−i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для через радикал (как ).
Определение[править | править код]
Мнимая единица — это число, квадрат которого равен −1. Т.е. — это одно из решений уравнения
Степени мнимой единицы[править | править код]
Степени повторяются в цикле:
Что может быть записано для любой степени в виде:
где n — любое целое число.
Отсюда:
где mod 4 — это остаток от деления на 4.
Возведение в комплексную степень является многозначной функцией.
Например, величина является многозначной, и представляет бесконечное множество вещественных чисел ():
Факториал[править | править код]
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
Корни из мнимой единицы[править | править код]
Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)
В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
Также корни из мнимой единицы могут быть представлены в показательном виде:
Иные мнимые единицы[править | править код]
К вопросу об интерпретации и названии[править | править код]
Обозначения[править | править код]
В языке программирования Python мнимая единица записывается как 1j.
В языке программирования Wolfram Language мнимая единица записывается как I.
См.также[править | править код]
Примечания[править | править код]
Ссылки[править | править код]
Ранее мы с вами разобрали пару крайне важных, в нашем мире, чисел: число Эйлера и число ПИ. Сегодня мы с вами узнаем еще об одном интересном и важном числе.
Мнимая единица, по сути, его нельзя назвать числом в привычном нам понимании. Это число не вещественное, а комплексное. Давайте пойдем по порядку.
Сперва история
Первые заметки о нем были обнаружены в записях Джероламо Кардано – итальянский математик живший в 16 веке. Он ввел его, когда решал кубические уравнения. Позже, когда ученые обнаружили эти записи, они начали производить с ним различные действия.
Основной вклад в развитие этой теории вложил ранее знакомый нам Леонард Эйлер. Тогда родился комплексный анализ, а позже и теория функций комплексного переменного (ТФКП). Леонард распространил основные функции в комплексную плоскость. Было сформулировано множество принципов, алгебраические действия не отличались от привычного вещественного анализа, но было сделано одно существенное допущение: в этой теории есть число, квадрат которого равен отрицательному числу. И это мнимая единица. Обозначается она как i, и такое название она получила благодаря все тому же Эйлеру (в некоторых других науках, таких как электротехника, встречается обозначение j, так как буква i занята для обозначения тока).
Для нахождения площади квадрата, мы возводим длину стороны этого квадрата в квадрат. То есть, мнимая единица – это сторона квадрата, у которого отрицательная площадь. Да, на реальности мы такого не встретим, именно по этому она называется мнимой. Но какой от нее тогда толк? Об этом немного позже.
Немного введу в курс дела
В комплексном анализе числовая прямая расширяется до комплексной плоскости, где осью абсцисс представлена вещественная прямая, а осью ординат – мнимая. Существует несколько способов записи комплексного числа: в виде пары чисел, в алгебраической форме, тригонометрической и вытекающей отсюда показательной.
Все формы представления в порядке, написанном выше
Самая красивая формула математики
Я хочу показать вам одну красивую формулу в математике, а для этого необходимо немного разобраться в комплексном анализе.
Давайте взглянем на комплексную плоскость поподробнее. На ней числа отмечаются точками, и каждой соответствует своя координата.
Но так же возможно векторное представление, где начало вектора лежит в начале координат, а конец на точке.
Благодаря этому возможно ввести показательное представление. Где число перед экспонентой показывает длину вектора, а угол в показателе равен углу между вещественной осью и этим вектором.
Это так называемая формула Эйлера (на самом деле это лишь частный случай этой формулы). И вся ее красота состоит в том, что она содержит в себе все знаменитые константы и числа.
Важность этого числа
Комплексный анализ очень важен для нашей жизни. В физике с его помощью описывают все волновые процессы. Вообще, говорят, что все волны и поля существуют в комплексном пространстве, а то, что мы видим, только тень «истинных» процессов. Квантовая механика, где и атом и другие материальные объекты — волны, делает такую трактовку более убедительной.
Так же, современная аэродинамика не обходится без ТФКП, где функции Жуковского могут давать необходимые профили крыла.
И это еще не все. Во многих отраслях так или иначе могут присутствовать элементы этой теории, поэтому ее важность нельзя отрицать.
Если данная статья была вам интересна, то не забывайте ставить пальцы вверх, я постарался написать для вас наиболее понятно. Так же подписывайтесь на канал, если еще не сделали этого! До скорых встреч и всего доброго! 🙂
×èñëî íàçûâàåòñÿ ìíèìîé åäèíèöåé.
Ìíèìàÿ åäèíèöà íå îòíîñèòñÿ ê ïðèâû÷íîìó íàì ìíîæåñòâó äåéñòâèòåëüíûõ ÷èñåë, à èñïîëüçóåòñÿ äëÿ ðàñøèðåíèÿ ýòîãî ìíîæåñòâà.
Ìíèìàÿ åäèíèöà — ýòî ÷èñëî, ó êîòîðîãî êâàäðàò ðàâíÿåòñÿ ìèíóñ åäèíèöå. Òî åñòü i — ýòî îäíî èç ðåøåíèé óðàâíåíèÿ:
Êîìïëåêñíàÿ ïëîñêîñòü. Âñå òî÷êè íà ïëîñêîñòè ñîîòâåòñòâóþò êîìïëåêñíîìó ÷èñëó. Êîîðäèíàòû a è b ñîîòâåòñòâóþò äåéñòâèòåëüíîé è ìíèìîé ÷àñòè êîìïëåêñíîãî ÷èñëà.
Ïðèìåðû ðàñ÷åòîâ ñ ìíèìîé åäèíèöåé.
Èíòåðåñíî òî, ÷òî âñå ìíîãî÷ëåíû èìåþò êîðíè, åñëè áðàòü â ðàñ÷åò ìíèìóþ åäèíèöó, åñëè òî÷íåå, êîëè÷åñòâî êîðíåé ðàâíÿåòñÿ ñòåïåíè ìíîãî÷ëåíà, ñ òî÷íîñòüþ äî êðàòíîñòè êîðíåé.
Ñòåïåíè i ïîâòîðÿþòñÿ öèêëè÷íî:
Ýòî ìîæíî çàïèñàòü äëÿ ëþáîé ñòåïåíè òàêèì îáðàçîì:
ãäå n — âñÿêîå öåëîå ÷èñëî.
×èñëî îêàçûâàåòñÿ âåùåñòâåííûì ÷èñëîì:
 ïîëå êîìïëåêñíûõ ÷èñåë êîðåíü n-îé ñòåïåíè èìååò n ðåøåíèé. Íà êîìïëåêñíîé ïëîñêîñòè êîðíè èç ìíèìîé åäèíèöû ðàñïîëîæåíû â âåðøèíàõ ïðàâèëüíîãî n-óãîëüíèêà, êîòîðûé âïèñàí â îêðóæíîñòü åäèíè÷íîãî ðàäèóñà.
Ýòî ñëåäóåò èç ôîðìóëû Ìóàâðà è òîãî, ÷òî ìíèìóþ åäèíèöó ìîæíî ïðåäñòàâèòü â òðèãîíîìåòðè÷åñêîì âèäå:
Êðîìå òîãî, êîðíè èç ìíèìîé åäèíèöû ìîæíî ïðåäñòàâèòü â ïîêàçàòåëüíîì âèäå:
Êîðíè êâàäðàòíûå èç ìíèìîé åäèíèöû.
Êîðíè êóáè÷åñêèå èç ìíèìîé åäèíèöû (âåðøèíû òðåóãîëüíèêà).
Êàëüêóëÿòîðû ïî àëãåáðå
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó àëãåáðû äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |



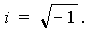
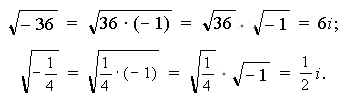
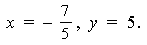
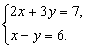


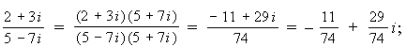
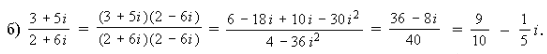
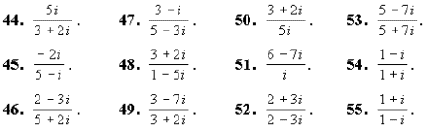
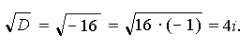
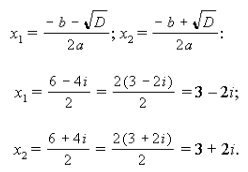
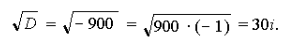
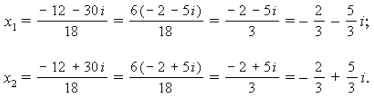
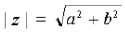
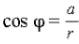 и
и 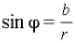

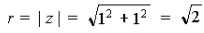
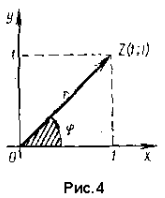 2) Изобразим число z геометрически (рис. 4). Мы видим, что числу z соответствует точка Z, лежащая в I четверти, и вектор z.
2) Изобразим число z геометрически (рис. 4). Мы видим, что числу z соответствует точка Z, лежащая в I четверти, и вектор z.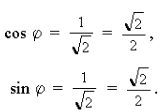
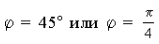
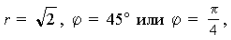
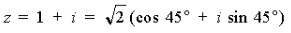
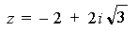 в тригонометрической форме.
в тригонометрической форме.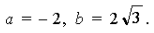
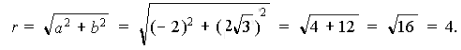
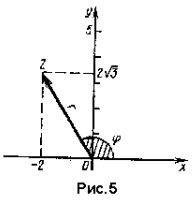 2) Изобразим число z геометрически (рис. 5). Мы видим, что числу z соответствует точка Z, лежащая во II четверти, и вектор z.
2) Изобразим число z геометрически (рис. 5). Мы видим, что числу z соответствует точка Z, лежащая во II четверти, и вектор z.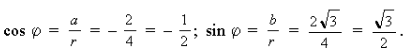
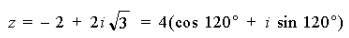
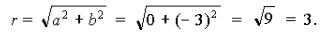
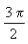 ,
,